![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
「数学ガールのお知らせメール」で週に一度の更新連絡をしています。ぜひ、ご登録ください。登録は無料です。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
テトラ「先輩! ユーリちゃん! いらしてたんですね」
僕「やっと会えた」
ユーリ「テトラさーん!」
僕とユーリは、 双倉図書館で開催されているイベント《いにしえの代数学》を巡っている。 会場にはパネルがたくさんあり、解説や数学の問題が書かれている。
ちょうど、後輩のテトラちゃんと会場でばったり出会ったところ。
テトラ「先輩たちはどのコーナーを回ったんですか?」
ユーリ「ディオファントスのところと……ぶらふま何とか」
僕「ディオファントス(第441回参照)とブラフマグプタ(第443回参照)だね。問題を解いたり、いろいろ考えたりしてたから、 かなりゆっくり回っているよ」
テトラ「あらら? あたしもディオファントスのところで問題を解いてました!」
ユーリ「ねーねー! テトラさんは、あの問題解けた? あの解けない問題」
僕「どっちだよ」
テトラ「何のことでしょう」
ユーリ「ほらほら、成り立つ $x$ がないやつ!」
問題3(再掲、(第442回参照))
文字はすべて正の整数とする。 $a,b,c,d$ をうまく選ぶと $$ \begin{cases} x^2 & = a + b \\ x^2 + a &= c^2 \\ x^2 + b &= d^2 \end{cases} $$ が成り立つような $x$ を求めよ。
(参考:ディオファントス『算術』第D巻問題11)
テトラ「はい。何とか証明できましたよ」
テトラちゃんは、ユーリと話すときにはずいぶん《お姉さんモード》の話し方になるみたいだなあ。
ユーリ「すげー! テトラさんも、無限降下法使ったの?」
テトラ「そうですよ。余りを利用しました」
ユーリ「さっすがー! それにしても、よく《$3$ で割った余り》を使うなんて思いつくにゃあ……」
テトラ「え? 《$3$ で割った余り》……でしたっけ?」
ユーリ「ふにゃ?」
僕「僕とユーリは問題3を考えるときに、《$3$ を法とした剰余》を使ったんだよ。 計算している途中で、 $$ 3x^2 = c^2 + d^2 $$ という式が出てきたから、この $3$ を使って何かできないかなって思ったんだ。 テトラちゃんは違うの?」
テトラ「あたしも同じ式 $3x^2 = c^2 + d^2$ を使って、 しかも剰余で考えたんですけど……でも、 $3$ じゃなくて $4$ を使いました。 《$4$ を法とした剰余》を使ったんです」
僕「へえ、 $4$ を使っても解けるんだ!」
ユーリ「解けないんだってば!」
僕「解けないことを証明したって言いたかったんだよ……」
僕とユーリはテトラちゃんが、 問題3を《$4$ を法とする剰余》を使って考えた話を聞くことにした。

テトラ「ディオファントスさんは正の整数 $x$ を求めようとしていました」
僕「そうだね。文字はぜんぶ正の整数だった」
ユーリ「お兄ちゃん、黙っててよ。テトラさんの話を聞かなきゃ」
僕「ごめんごめん」
テトラ「正の整数に限らず、整数を考えるときには偶数・奇数の区別に注目するのが大事でした。 偶数・奇数の区別というのは、 もちろん、 $2$ で割ったときに余りが $0$ になるか、 $1$ になるかということです」
僕とユーリは黙って頷く。
そうそう。《偶奇を考える》のは大事だ。
テトラちゃんは自分が考えた道すじをていねいに話していく。
テトラ「ところで、 問題3には $x^2$ が出ていたので、 $2^2 = 4$ で割った余りを考えてみようと思いました。 具体的にいうと、こういうことです」
ユーリ「……」
テトラ「整数を $4$ で割った余りは $0,1,2,3$ の $4$ 通りどれかになるんですけど、 整数を二乗した平方数にすると話が変わります。 平方数を $4$ で割った余りは $0$ と $1$ のどちらかにしかなりません」
ユーリ「へー! それって、テトラさんが発見したの?!」
テトラ「いえいえ。以前に《$4$ で割った剰余》を調べたことがあって、それを思い出した——というのが正確です」
僕「平方数を $4$ で割った余りは $0$ か $1$ にしかならない。 そのことは証明もできるよね」
テトラ「はい。あたしも証明しました。どんな整数 $x$ でも、整数 $n$ を使って——
$$ \left\{ \begin{align*} x &= \BLUEFOCUS{4n} + \REDFOCUS0 \\ x &= \BLUEFOCUS{4n} + \REDFOCUS1 \\ x &= \BLUEFOCUS{4n} + \REDFOCUS2 \\ x &= \BLUEFOCUS{4n} + \REDFOCUS3 \end{align*} \right. $$ ——のどれかで表せます。そして、それぞれの場合について平方数 $x^2$ を作ってみます」【 $x = \BLUEFOCUS{4n} + \REDFOCUS0$ の場合】 $$ \begin{align*} x^2 &= (\BLUEFOCUS{4n} + \REDFOCUS0)^2 \\ &= 16n^2 \\ &= \BLUEFOCUS{4(4n^2)} + \REDFOCUS0 \end{align*} $$ なので、 $4$ で割った余りは $\REDFOCUS0$ です。
【 $x = \BLUEFOCUS{4n} + \REDFOCUS1$ の場合】 $$ \begin{align*} x^2 &= (\BLUEFOCUS{4n} + \REDFOCUS1)^2 \\ &= 16n^2 + 8n + 1 \\ &= \BLUEFOCUS{4(4n^2 + 2n)} + \REDFOCUS1 \end{align*} $$ なので、 $4$ で割った余りは $\REDFOCUS1$ です。
【 $x = \BLUEFOCUS{4n} + \REDFOCUS2$ の場合】 $$ \begin{align*} x^2 &= (\BLUEFOCUS{4n} + \REDFOCUS2)^2 \\ &= 16n^2 + 16n + 4 \\ &= \BLUEFOCUS{4(4n^2 + 4n + 1)} + \REDFOCUS0 \end{align*} $$ なので、 $4$ で割った余りは $\REDFOCUS0$ です。
【 $x = \BLUEFOCUS{4n} + \REDFOCUS3$ の場合】 $$ \begin{align*} x^2 &= (\BLUEFOCUS{4n} + \REDFOCUS3)^2 \\ &= 16n^2 + 24n + 9 \\ &= \BLUEFOCUS{4(4n^2 + 6n + 2)} + \REDFOCUS1 \end{align*} $$ なので、 $4$ で割った余りは $\REDFOCUS1$ です。
ユーリ「にゃるほど」
テトラ「ですから、平方数を $4$ で割った余りは $0$ または $1$ です。 そこで、問題3から得られる $$ 3\REDFOCUS{x^2} = \BLUEFOCUS{c^2} + \GREENFOCUS{d^2} $$ を見ますと、これは $$ 3 \times \REDFOCUS{\textrm{平方数}} = \BLUEFOCUS{\textrm{平方数}} + \GREENFOCUS{\textrm{平方数}} $$ という形になっていることがわかります」
ユーリ「待って待って! テトラさん、そっから先、ユーリも考えたい!」
テトラ「いいですよ。待ってますね」
《お姉さんモード》のテトラちゃんがにっこりした。
ユーリはここまでの話から、 $c,d$ が正の整数のとき、 $$ 3x^2 = c^2 + d^2 $$ を満たす正の整数 $x$ は存在しないことの証明にすぐ手が届くことに気付いたんだな。

ユーリ「……たぶん、できた!」
僕「どんな感じ?」
ユーリ「こんな感じ」
ユーリの説明
さっき、テトラさんは《平方数を $4$ で割った余りは $0$ または $1$》って話をしてた。
だから、
てことは、 $3\REDFOCUS{x^2} = \BLUEFOCUS{c^2} + \GREENFOCUS{d^2}$ になるなら、 $3\REDFOCUS{x^2}$ と $\BLUEFOCUS{c^2} + \GREENFOCUS{d^2}$ は両方とも、 $4$ で割った余りが《$0$ になる》はず! つまり、 両方とも $4$ の倍数になる!
ついでに、 $\BLUEFOCUS{c^2}$ と $\GREENFOCUS{d^2}$ も $4$ の倍数になる。 だって、 $0+0$ のはずだから。
あ・と・は、無限降下法!
テトラ「ユーリちゃん、すごいですねえ!」
ユーリ「へへ」
僕「すごいすごい……あ、でも、無限降下法に行くにはもう少し補足があった方がいいよね」
ユーリ「えー! そーお?」
僕「$3x^2 = c^2 + d^2$ を満たす $(x,c,d)$ から、 $3x_1^2 = c_1^2 + d_1^2$ を満たす $(x_1,c_1,d_1)$ を作るところまで行きたいなあ」
僕の補足
$3\REDFOCUS{x^2}$ と、 $\BLUEFOCUS{c^2}$ と、 $\GREENFOCUS{d^2}$ がぜんぶ $4$ の倍数になる——という続きだよ。
$3\REDFOCUS{x^2}$ が $4$ の倍数で、 $3$ と $4$ は互いに素だから $\REDFOCUS{x^2}$ は $4$ の倍数になる。 このとき $x$ は $2$ の倍数になる。 $x$ は正の整数だから、 $x = 2x_1$ という正の整数 $x_1$ が存在して、 $x_1 < x$ を満たす。
同じように考えて、 $\BLUEFOCUS{c^2}$ と $\GREENFOCUS{d^2}$ が $4$ の倍数だから、 $c = 2c_1, d = 2d_1$ という正の整数 $c_1,d_1$ が存在する。
したがって、 $$ 3\REDFOCUS{x^2} = \BLUEFOCUS{c^2} + \GREENFOCUS{d^2} $$ から $$ 3\REDFOCUS{(2x_1)^2} = \BLUEFOCUS{(2c_1)^2} + \GREENFOCUS{(2d_1)^2} $$ が成り立つ。両辺を $4$ で割ると $$ 3x_1^2 = c_1^2 + d_1^2 $$ になる。
同じ議論を繰り返して、 $$ (x,c,d) \to (x_1,c_1,d_1) \to (x_2,c_2,d_2) \to \cdots $$ と続けていくことができる。このとき $$ x > x_1 > x_2 > \cdots $$ になるが、これは $x,x_1,x_2,\ldots$ が正の整数であることに反する。 したがって、問題2を満たす $x$ は存在しない。
ユーリ「あっ、そんなことユーリもわかってたもん!」
僕「ユーリがわかってたことは僕もわかってたよ。だから念のための補足」
ユーリ「むー……」
テトラ「あっちのコーナーに行きませんか? あたしは一通り回ったんですが、 あっちのコーナーにはアルゴリズムという言葉のもとになった数学者のコーナーがありましたよ」
ユーリ「あるごりずむ?」
テトラ「アル=フワーリズミーさんですね」
フワーリズム(ホラズム)地方(図中のChoresmienの部分)
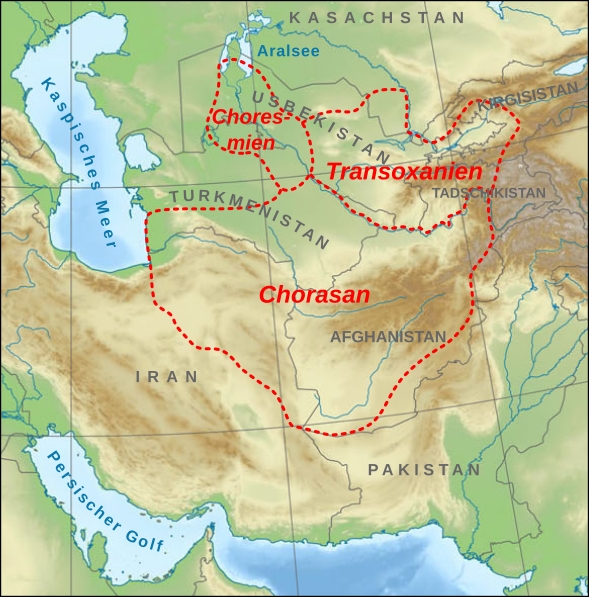
Image by Lencer, licensed under
CC BY-SA 3.0,
based on Relief Map of Middle East.jpg by User: Виктор and
Khorasan-Mawaralnahr-Khwarizm.jpg by User: Phoenix2,
via Wikimedia Commons
アル=フワーリズミー
アル=フワーリズミーは9世紀のイスラム世界の数学者で、数学・天文学・地理学に業績を残した。 彼は『アル=ジャブルとアル=ムカーバラの書』や 『インド数字による計算法』という数学書を書いた。 名前の「アル=フワーリズミー」は現代のアルゴリズムという言葉のもとになった。 もともとは「フワーリズム(ホラズム)出身」という意味である。
ユーリ「ある・いこーる・ふわーりずみー」
テトラ「途中のイコール(=)はイコールと読むわけじゃなくて、区切り文字ですね」
ユーリ「ある・ふわーりずみー」
テトラ「アラビア語で《アル》というのは英語の《the》に相当する定冠詞だそうです。 ですから、アラビア語に由来する言葉はよく『アル』で始まりますよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2025年3月21日)