![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
僕とテトラちゃんは、 村木先生の《カード》に書かれていたベクトル空間の定義を《二人三脚読み》してきた。 僕がぜんぶを教えるのではなく、 テトラちゃんと僕とで書かれていることを一緒に読もうというのだ。
僕たちは、 文章を細かく分解して読んだり(第385回参照)、 数学辞典を読んで例を作ったり(第386回参照)、 《である例》と《ではない例》を考えたり(第387回参照)、 写像の定義を《カード》にあてはめて考えたりしてきた(第388回参照)。 そしてようやく(1)〜(4)まで読み終えたところ(第389回参照)。
僕「……で、ここまでの準備を終えて、 (1)〜(4)の性質を持つスカラー倍が定義されているときの $V$ のことを《$K$ 上のベクトル空間》といえた。 これがベクトル空間の定義になるね」
テトラ「はい……その一つ一つはわかってるつもりです。 そうなんですが、全体としてはまだわかっていないみたいです。 《これ》がベクトル空間ですね! と手に取って眺めることができたらいいんですが……」
僕「じゃあ、手に取って眺めてみようよ」
テトラ「ど、どうやってですか?」
僕「もちろん、ベクトル空間の具体例を眺めるんだよ! 僕たちが読んできた、この《カード》に合致する例を見てみようよ」
テトラ「ああ、そうですね。《例示は理解の試金石》にしたがって、 あたしたちの——というか、あたしの理解をテストするわけですね。この《カード》の理解です」
僕とテトラちゃんはあらためて村木先生からの《カード》を読み返した。
村木先生の《カード》
(1)$K$ の任意の元 $a$ と、 $V$ の任意の元 $x,y$ に対して、$$a(x + y) = ax + ay$$が成り立つ。
(2)$K$ の任意の元 $a,b$ と、 $V$ の任意の元 $x$ に対して、$$(a + b)x = ax + bx$$が成り立つ。
(3)$K$ の任意の元 $a,b$ と、 $V$ の任意の元 $x$ に対して、$$(ab)x = a(bx)$$が成り立つ。
(4)$K$ の単位元を $1$ とすると、 $V$ の任意の元 $x$ に対して、$$1x = x$$が成り立つ。
※松坂和夫『代数系入門』を参考にしています。
僕「うん。例として、まず考えるのは……っとっとっと。 僕が例を出しちゃダメだった。テトラちゃん、どうぞ!」
テトラちゃんは、チャームポイントの大きな目をぱちぱちさせてから話し出した。
テトラ「はい。あたしが最初に確かめたいのはやはり、矢印との関係です。 あたしはベクトルといわれると、矢印を思い浮かべますから。 矢印の足し算は平行四辺形を使って対角線の矢印になる——みたいに」
矢印ベクトルの足し算

僕「うん、そうだよね」
テトラ「でも、先輩がおっしゃったように、 この《カード》に書かれているのは、矢印ベクトルよりも、もっと一般的なベクトルの定義ということですよね(第383回参照)」
僕「そうそう。僕たちがよく考えている矢印ベクトルはもちろんベクトルの一種なんだけど、 この《カード》では、もっと一般的にベクトルを定義している。 そして、ここで定義されているベクトルには矢印がまったく出てこない」
テトラ「はい、そこです! そこが、そもそものあたしの悩みどころでした。 《カード》を読んでいて、 いきなり、このような $V$ をベクトルと呼ぶ! とベクトルを定義したからです。 え、矢印はどこで出てきたの?!と思ってしまいました」
僕「びっくりしちゃうよね。ところで、テトラちゃんにあえてツッコミを入れるけど……」
テトラ「はい?」
僕「《カード》に出てきた $V$ はベクトルじゃなくて、ベクトル空間だよ。 $V$ がベクトルなんじゃなくて、 $V$ の元がベクトル」
テトラ「あ、そうですね。そうでした。大丈夫です。それはわかっています……ええと、 それで、矢印が、 ここで定義されているベクトルになっていることを確かめればいいんですね?」
僕「そう! そういうことになるね」
テトラ「は、はい。そうですね。ぜんぶ具体的に話せばいいんですよね。 では、ここでは平面上の矢印で考えることにしますっ!」
ミルカ「テトラの声が聞こえた」
背後から静かな声が聞こえて、僕はびっくりした。
ミルカさんはいつでも風のように現れる。
テトラ「ミルカさん!」
登場人物紹介(追加)
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
僕「驚いたよ……ぜんぜん気付かなかった」
ミルカ「今シーズン、出番がなさそうだから、せめてエピソード10には顔を出しておこうかと思ったんだ」
僕「メタ発言自重」
ミルカ「ベクトル空間?」
ミルカさんは、僕の肩越しに村木先生の《カード》をのぞき込んで言った。
テトラ「はい、そうです。ベクトル空間の定義を読んでいたんです」
僕「……」
僕は複雑な気持ちだった。
僕はミルカさんが来てくれてうれしいと思った。でも、それと同時にちょっと残念でもあった。
これまでテトラちゃんと僕は一歩一歩《二人三脚読み》をしてきた。 でもここで《饒舌才媛》のミルカさんがすらすらとベクトル空間の講義をしてしまったら、 何だか楽しみを奪われたような気持ちになりそうだからだ。
平面上の矢印が、確かにベクトルの定義に合致していることは僕にも確かめられるし……と、そんなふうに思う僕は、了見が狭いんだろうか。
もしかしたら僕はテトラちゃんに、僕の《いいところ》を見せたいだけなのか。
いや、そういう気持ちもなくはないけれど、それだけじゃない。
自分なりに考えたいところで、 誰かからポンと答えを見せられたらがっかりするだろう。
そして僕は気付く。 テトラちゃんが僕によそよそしい態度を取ったことがあった。 あれはまさに、いまの僕と同じ気持ちだったのかもしれない(第381回参照)。
そうだ。だとしたら僕は——言葉にして伝えるべきなんだ。
ミルカ「君は何をぼうっとしてるのか」
僕「うん、あのね、ミルカさん。 いまはちょうどベクトル空間の定義を読み終えて、 テトラちゃんが例を作るところだったんだ」
テトラ「そうです。平面上の矢印ベクトルが、本当にベクトルであることを確かめるんですっ!」
ミルカ「ふむ」
僕「それでね。ミルカさんはベクトル空間のことをよく知ってるだろうけれど——」
ミルカ「私はあまり余計な口出しをするな、と」
僕「言い方」
ミルカ「そんな野暮なことはしない。答えを先取りして言いたがるほど、私は子供じゃない」
(本当にそうかなあ)と思わないではないけれど、ともかく、僕の気持ちがミルカさんに伝わってよかった。
そうなんだ。ちゃんと言葉にして伝えれば無用な誤解は避けられる。 僕たちは数学を考える楽しみを知っている仲間だからだ。
ミルカ「私のことは気にしなくていい。続ければ?」
テトラ「は、はい。いまあたしがやろうとしているのは、 平面上の矢印を、この《カード》の定義に当てはめてみることです。 もしもぴったり当てはまるのであれば、平面上の矢印が確かにベクトルの例になっているといえて、矢印ベクトルの名前にふさわしくなります」
僕「そうだね」
テトラ「定義に当てはめて考えるというのは、 定義に出てくる文字や言葉が、矢印の場合は何に相当するかをいえばいい——わけですよね」
僕とミルカさんは黙って肯いた。
いまはテトラちゃんが語る番なのだ。
テトラ「《カード》では、 $K$ は体で、 $K$ の元をスカラーと呼んでいました。 あたしはこれを実数にして考えればいいと思います。 つまり $K$ として実数体 $\REAL$ を考え、実数のことをスカラーと呼ぶことにするんです。 どうしてそう思ったかというと、あたしは矢印ベクトルをスカラー倍することを知っていて、 そのときには実数を使ったからです。たとえば矢印ベクトルを $2$ 倍するとこうなります」
矢印ベクトルのスカラー倍($2$ 倍)

僕「うん」
ミルカ「……」
テトラ「それから《カード》では、 $V$ は加法群で、 $V$ の元をベクトルと呼んでいました。 ですから、あたしは $V$ を平面上の矢印全体の集合として考えればいいと思いました。 というのは、あたしはいま矢印のひとつひとつをベクトルのひとつひとつとしたいわけですから、 矢印をぜんぶ集めたものが $V$ ですよね?」
僕「そう! そうなる。 $V$ として平面上の矢印全体の集合を考える」
テトラ「そして、この $V$ 、つまり平面上の矢印全体の集合は足し算ができますから、加法群ということができます」
僕「うん、そうだね。 ちゃんと確かめるためには加法群の定義と照らし合わせることになるけれどね。 矢印同士の足し算、つまり加法が結合法則を満たしていて、 単位元に相当する矢印があって、どの矢印に対しても、逆元に相当する矢印がある——そのことを確かめれば群であることがいえる。 そして交換法則を満たしているかを確かめれば、さらに加法群だといえる。 平面上のすべての矢印——さまざまな長さの、さまざまな向きの無数の矢印——同士が自由に足し算できるイメージだね」
平面上のすべての矢印(のイメージ)

テトラ「そうですね」
ミルカ「そうかな?」
テトラ「え?」
ミルカ「いまの会話で疑問が生じた。 私は答えを知っているけれど、答えは言わない。口止めされたからな。 だが、疑問を提示するのはかまわないだろう?」
僕「もちろんいいけど、加法群であることを確かめるのは、交換法則が成り立つ群であることを確かめればいいはずだよね?」
ミルカ「疑問というのはそこじゃない。 テトラは——そして君も——平面上の矢印全体の集合を、《カード》に述べられた $V$ として考えたいようだ。 ところで矢印というのはどういう定義?」
テトラ「平面上にある矢印ですから、ええとですね。ある点から別の点に——ちょっと待ってください。 考えます…… はい、大丈夫です。平面上の二点があって、始点と終点だと考えて、その組を矢印だとすればいいですね」
僕「そうだね。矢印は始点と終点の組で考えればいい」
ミルカ「そうすると、始点と終点の組を $V$ の元と考えることになる」
テトラ「そうですね」
ミルカ「それでは、 $V$ の元同士の加法はどう定義する?」
テトラ「矢印同士の足し算は、平行四辺形の対角線で考えればいいのではないでしょうか」
ミルカ「二つの矢印の始点が一致するならそれでいい。しかし、こんな疑問が生じる。 始点が一致しない場合、二つの矢印はどうやって足せばいい?」
テトラ「それは、始点が一致するように矢印を平行移動してから足すんですよね?」
始点が一致しない矢印は、平行移動してから足す
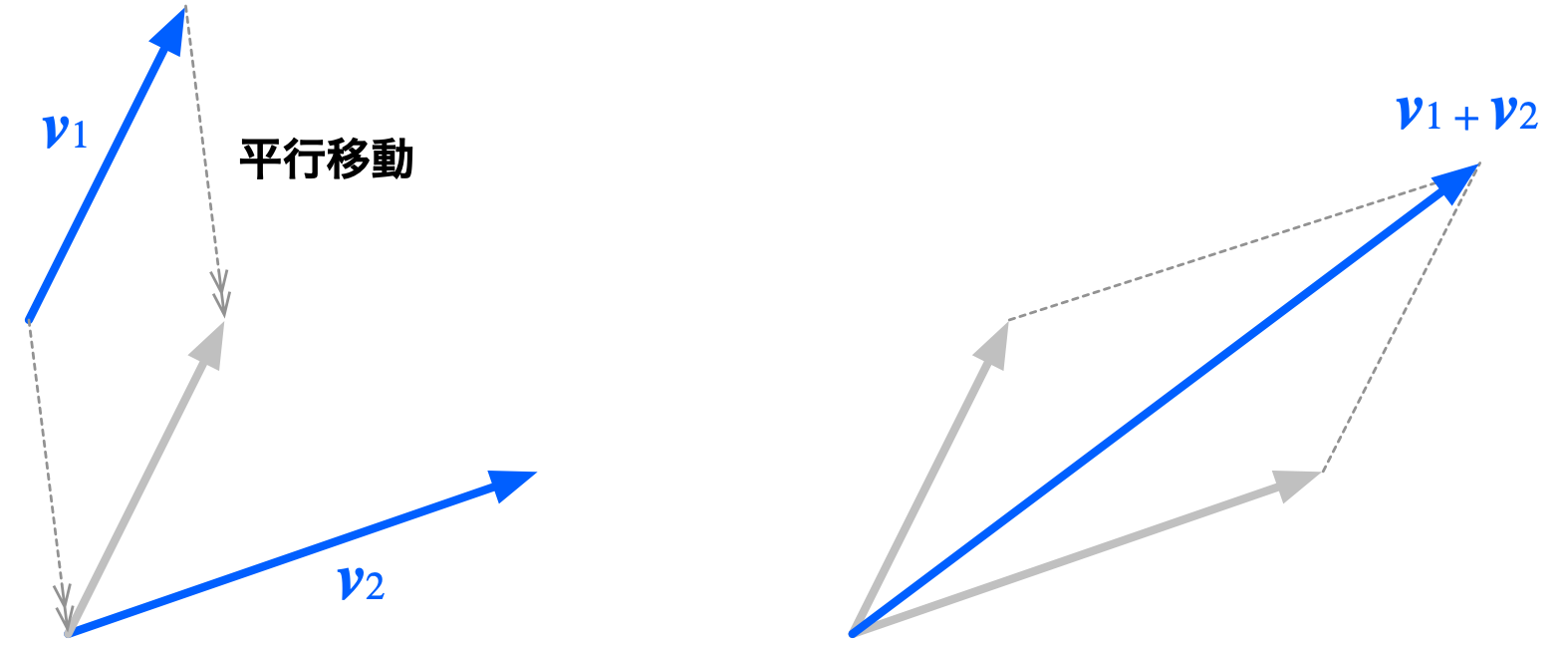
ミルカ「矢印 $\BV_1$ を平行移動して得られた矢印は、 $\BV_1$ と等しいといえるだろうか」
僕「そうか! 平行移動したときに重なる矢印同士は等しいと見なす必要があるんだった!」
ミルカ「私は答えを言ってない。君が言ったんだ」
テトラ「ああ……それ、もしかして、以前お聞きした同値関係で割るというお話ですか?」
ミルカ「その通り。 矢印をベクトルの定義に厳密に当てはめて考えるためには、 平行移動で一致する矢印を同一視する同値関係を定義して、 その同値関係で矢印全体の集合を割る。 そのときの同値類がベクトルとなる」
平行移動で一致する矢印を同一視する同値関係を使って、矢印全体の集合を割る
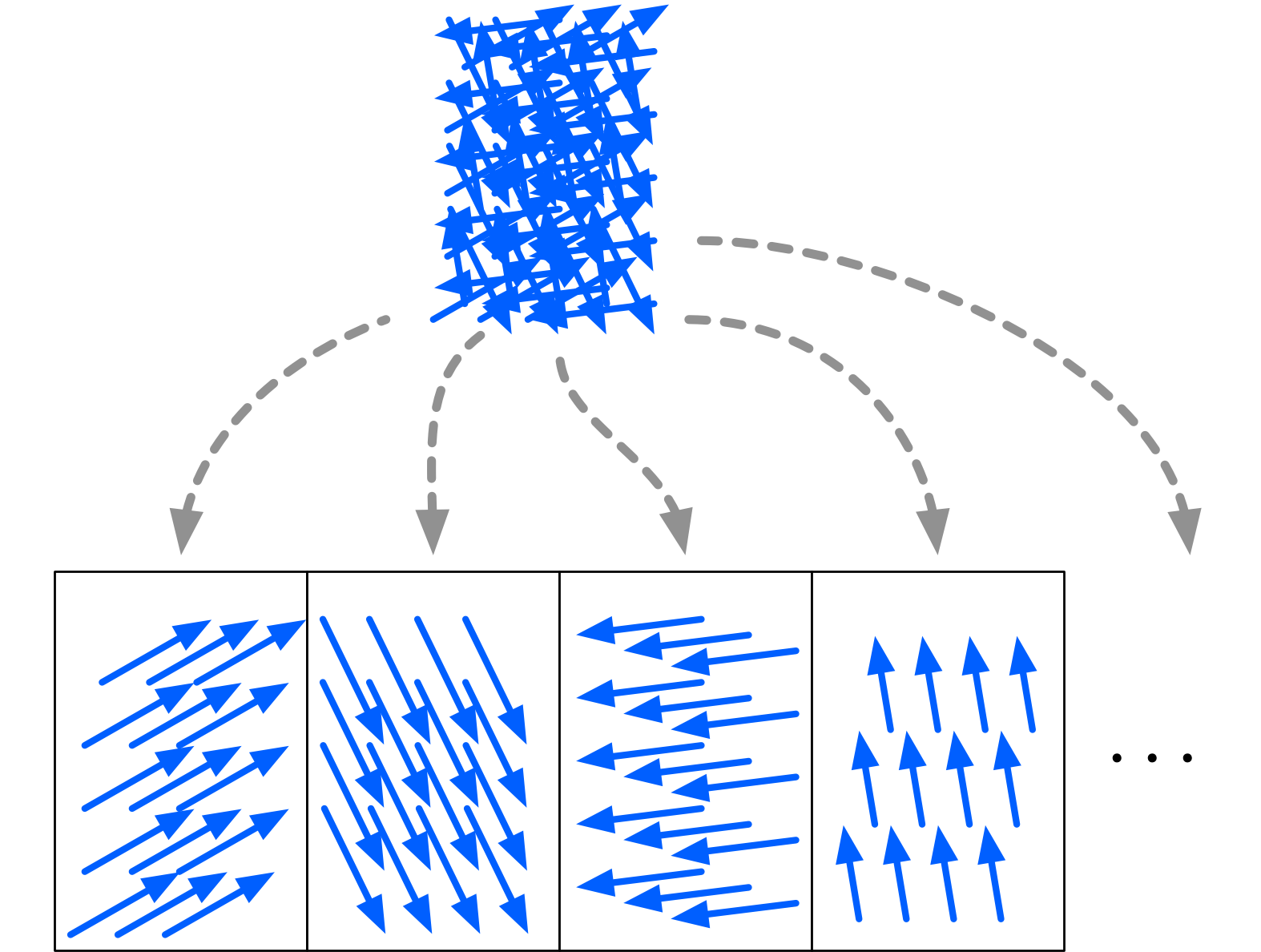
テトラ「ずいぶんやっかいな話になってしまうんですね」
ミルカ「ここでユーリのCMが入る」
【CM】
ユーリ「はーい、今回はCM担当のユーリでーす。 矢印同士の足し算をどう考えるか、引き算をどうするか、 そして同値関係で割るって何? というところまで突っ込んで考えるお話は、 『数学ガールの秘密ノート/ベクトルの真実』でどーぞ! ベクトルの真実がこの一冊に!」
僕「メタ発言自重……っと、 始点を原点に一致させた矢印だけを考えればもっとシンプルにいけるんじゃない?」
ミルカ「それはそう。座標平面上の点 $\VECV{x}{y}$ を一つのベクトルだと考えるわけだ。 それは、平行移動で一致するすべての矢印の集合——つまり先ほどの同値類から、 原点に始点を持つ矢印を代表元として選んだことに相当する」
原点を始点に持つ矢印だけを考えることにする
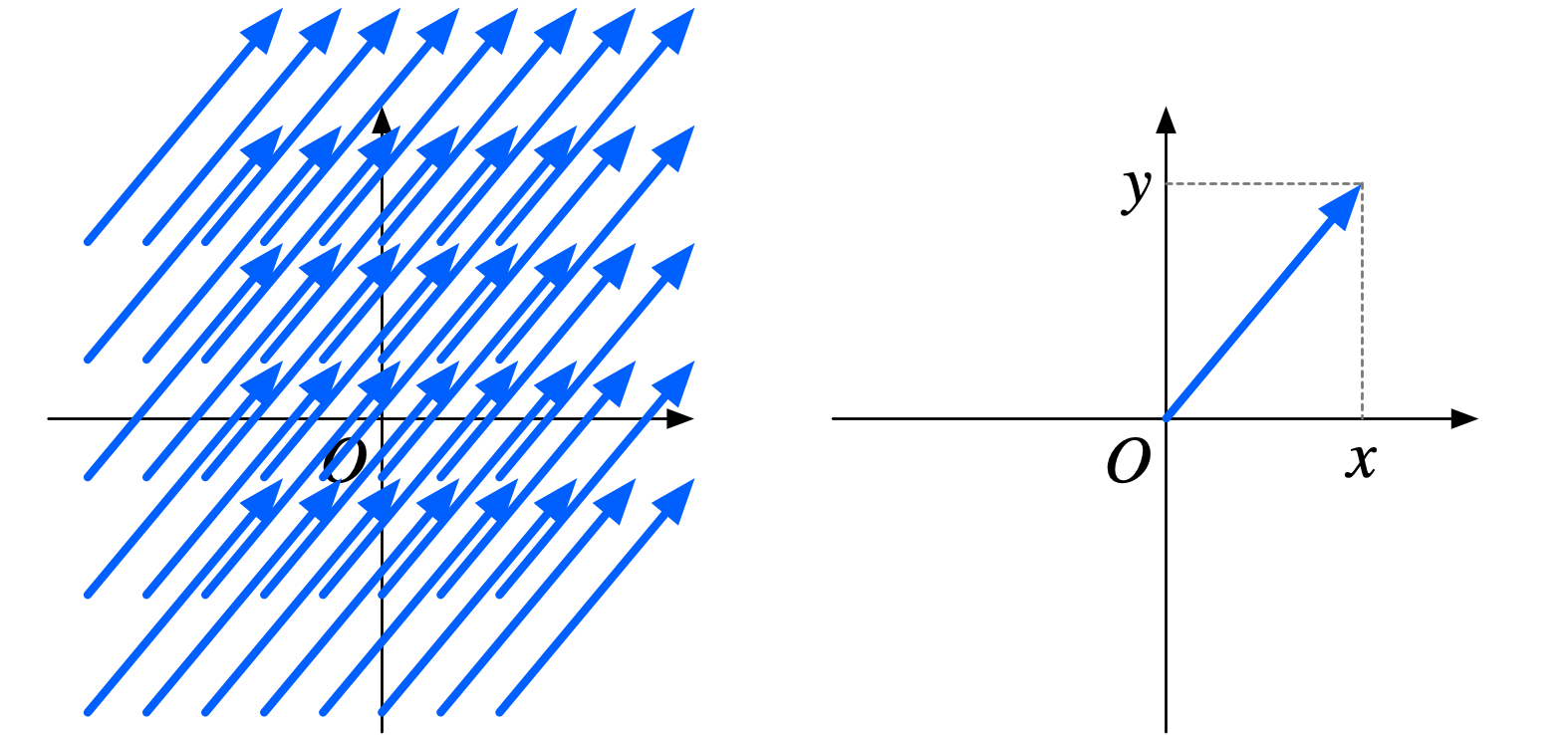
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2023年4月7日)