![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「お兄ちゃん! パスカルの三角形って知ってる?」
ユーリは僕のいとこ。
近所に住む中学生だ。
小さいときから一緒に遊んでいるから、 僕のことを《お兄ちゃん》と呼ぶ。
彼女は休みになるといつも僕の部屋に遊びに来るのだ。
僕「パスカルの三角形? もちろん、知ってるよ」
ユーリ「はいっ、一点減点!」
僕「ちょっと待った。僕はパスカルの三角形を知ってるって言ったんだよ。 どうしてそれで一点減点になるんだ?」
ユーリ「んーんんん? お兄ちゃん、何て言ったってー?」
僕「パスカルの三角形のことなら知ってるよって」
ユーリ「違う、違ーう! その前に《もちろん》って言ったでしょ。 それで一点減点。先生たるもの、そんなに簡単に《もちろん》なんて言っちゃいかんでしょ」
僕「どういう理屈なんだ、それ? そもそも先生じゃないし」
ユーリ「まーそりゃいいや。お兄ちゃんは、パスカルの三角形って知っているよね、もちろん」
僕「ユーリは《もちろん》って言ってもいいんかい」
ユーリ「ユーリは先生じゃないもん」
僕「僕だって先生じゃないよ」
ユーリ「いーから、とっとと数学を進めてくれたまえ。こーゆー小芝居を嫌う読者もいるのだよ」
僕「メタ発言自重」
ユーリ「とにかく、パスカルの三角形!」
僕「パスカルの三角形って、こういうものだね」
僕は、手元のA4コピー用紙にパスカルの三角形を書いた。
パスカルの三角形(Pascal's triangle)
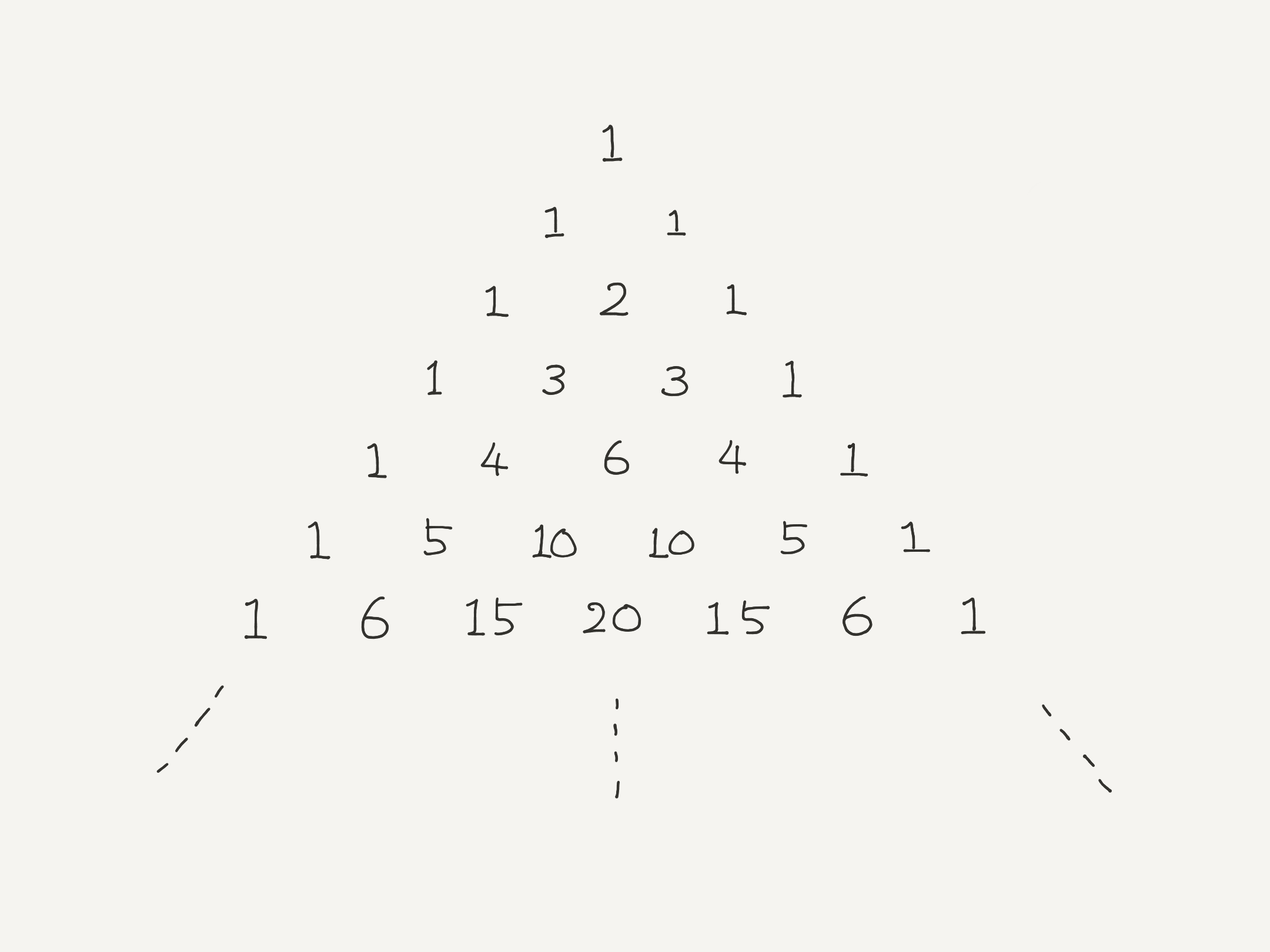
ユーリ「それそれ。 このパスカルの三角形って、 いまお兄ちゃんが書いた通り、 上の数を二つ足して下の数を作るわけでしょ? たとえば、ここの $4$ と $6$ を足して、すぐ下の $10$ を作るみたいに」
パスカルの三角形の作り方
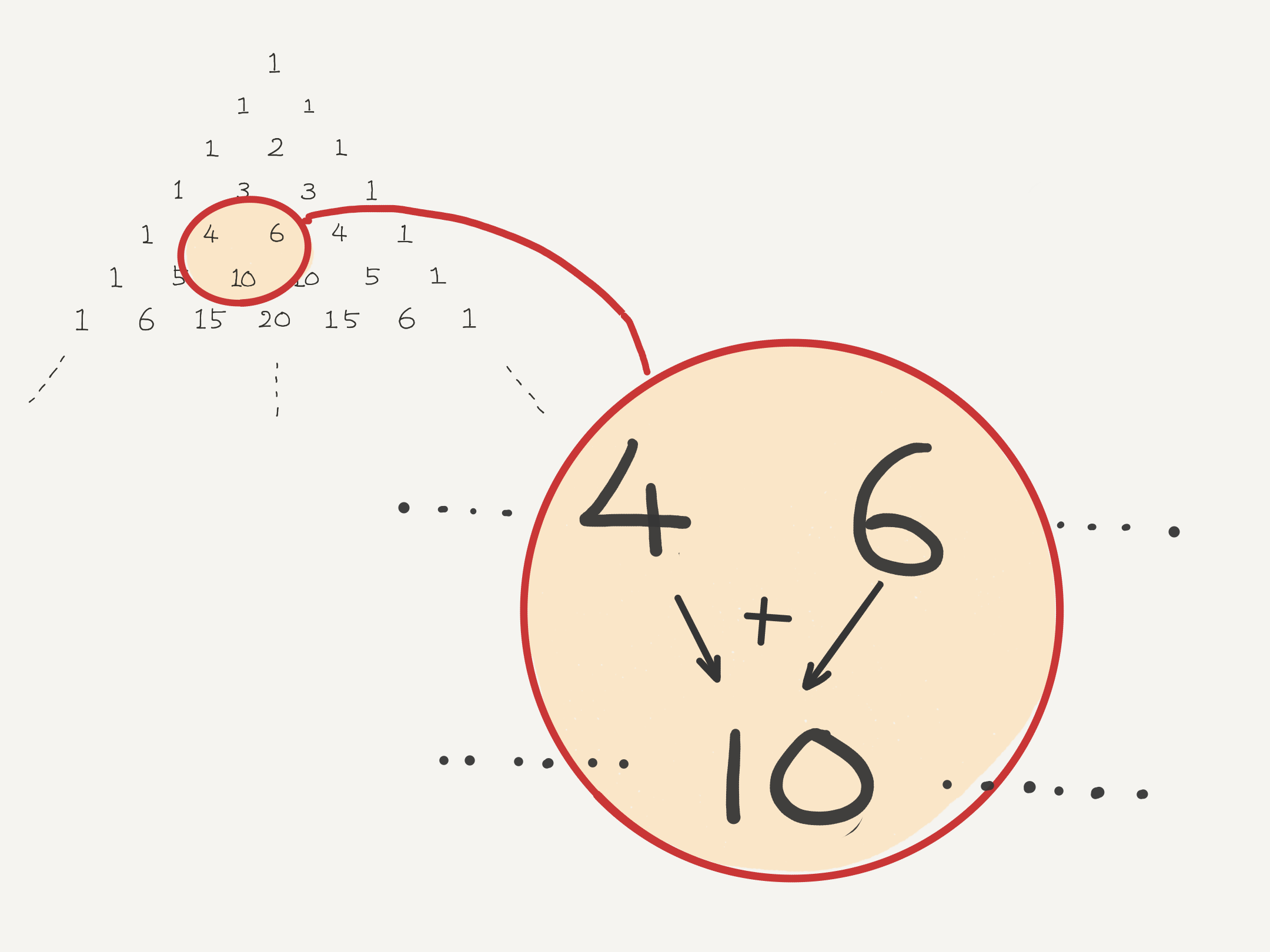
$$ 4 + 6 = 10 $$
僕「そうだね。パスカルの三角形は行ごとに作っていく。 上の行の数の並びから、下の行の数の並びを作って、下に進んでいく。 各行に並ぶ数はどうするかというと……
パスカルの三角形は行ごとに作っていく。
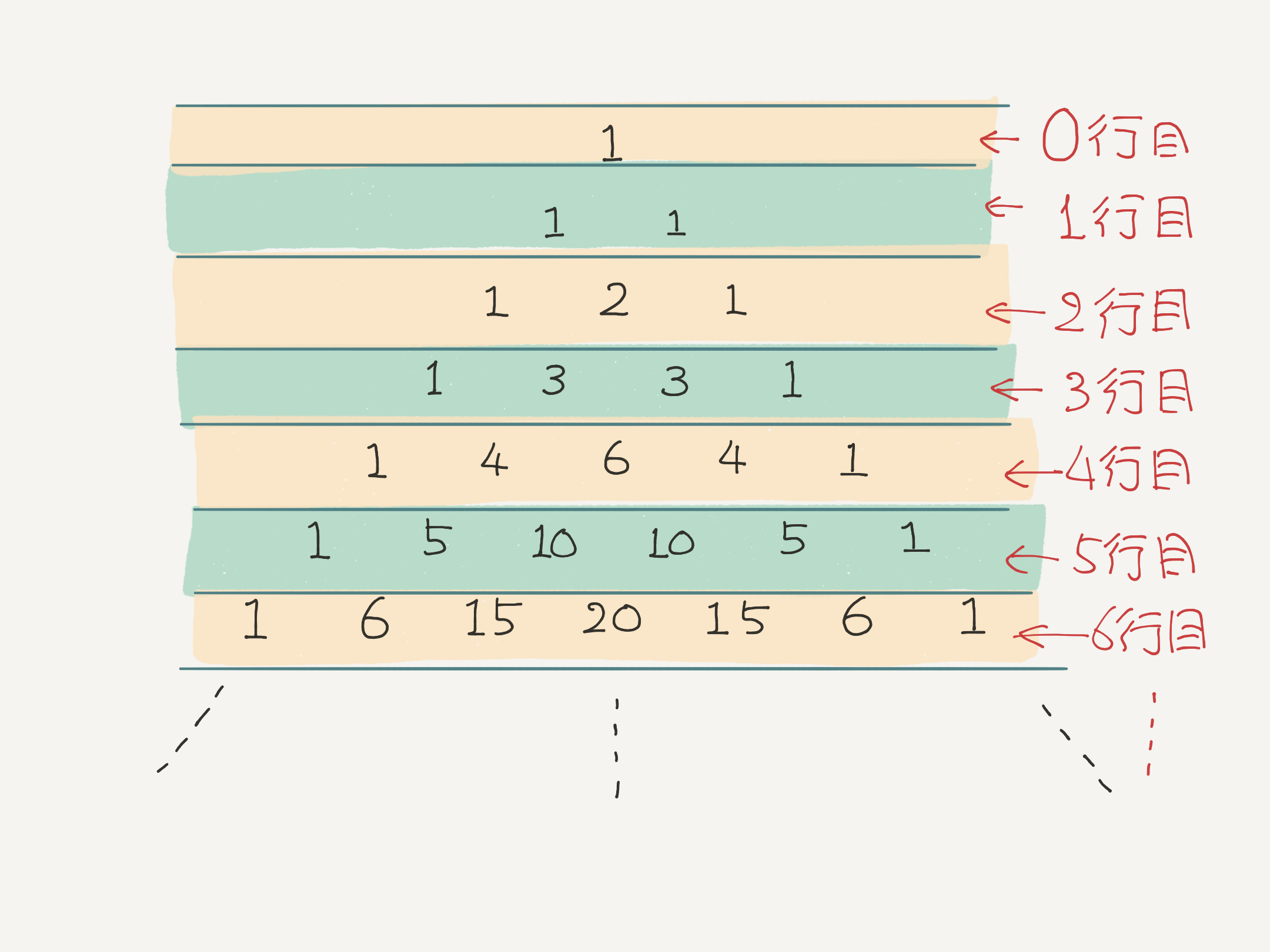
両端の数は、 $1$ にする。
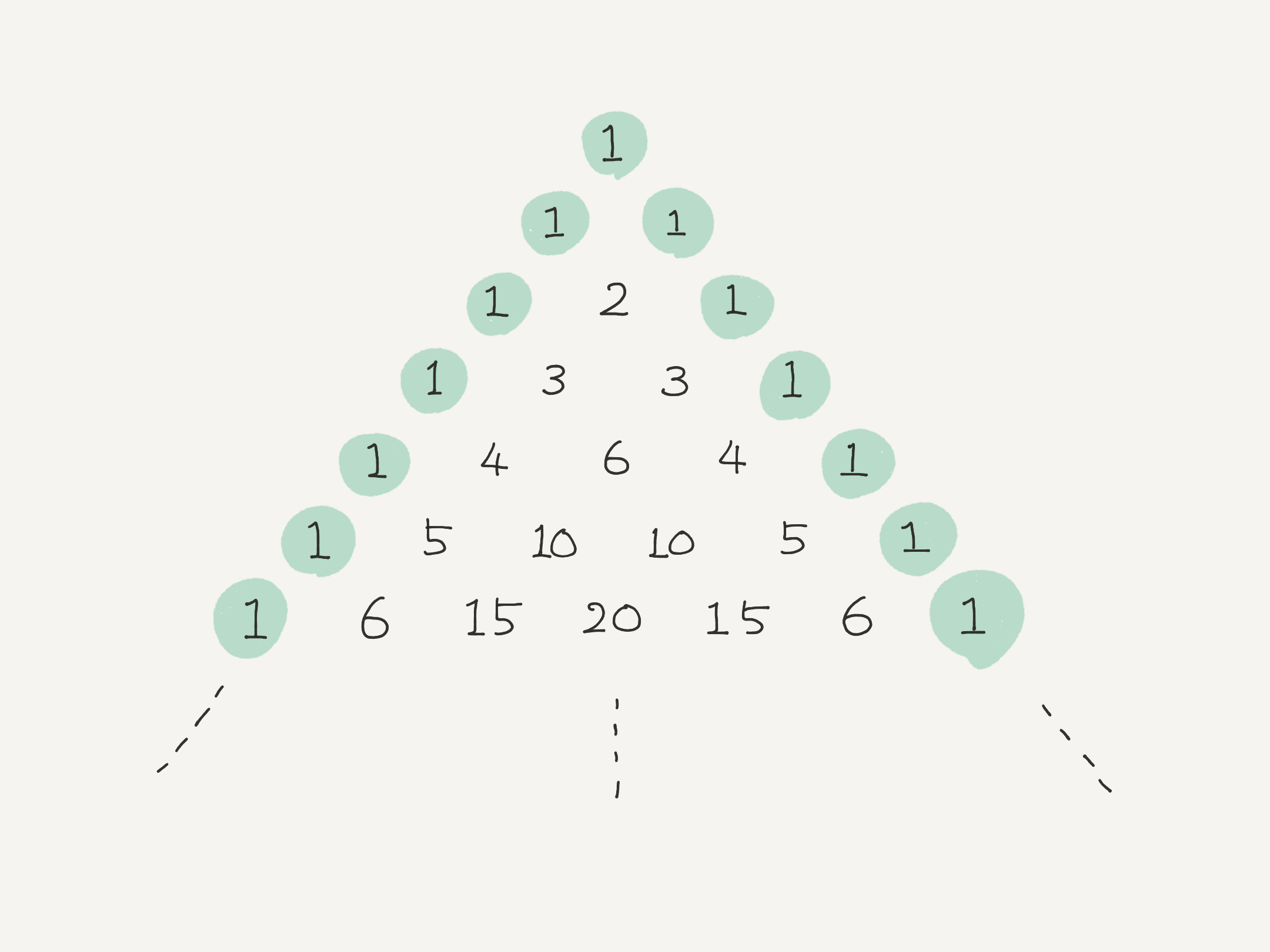
両端以外の数は、ちょうど上に並んだ二つの数を足し合わせた結果にする。
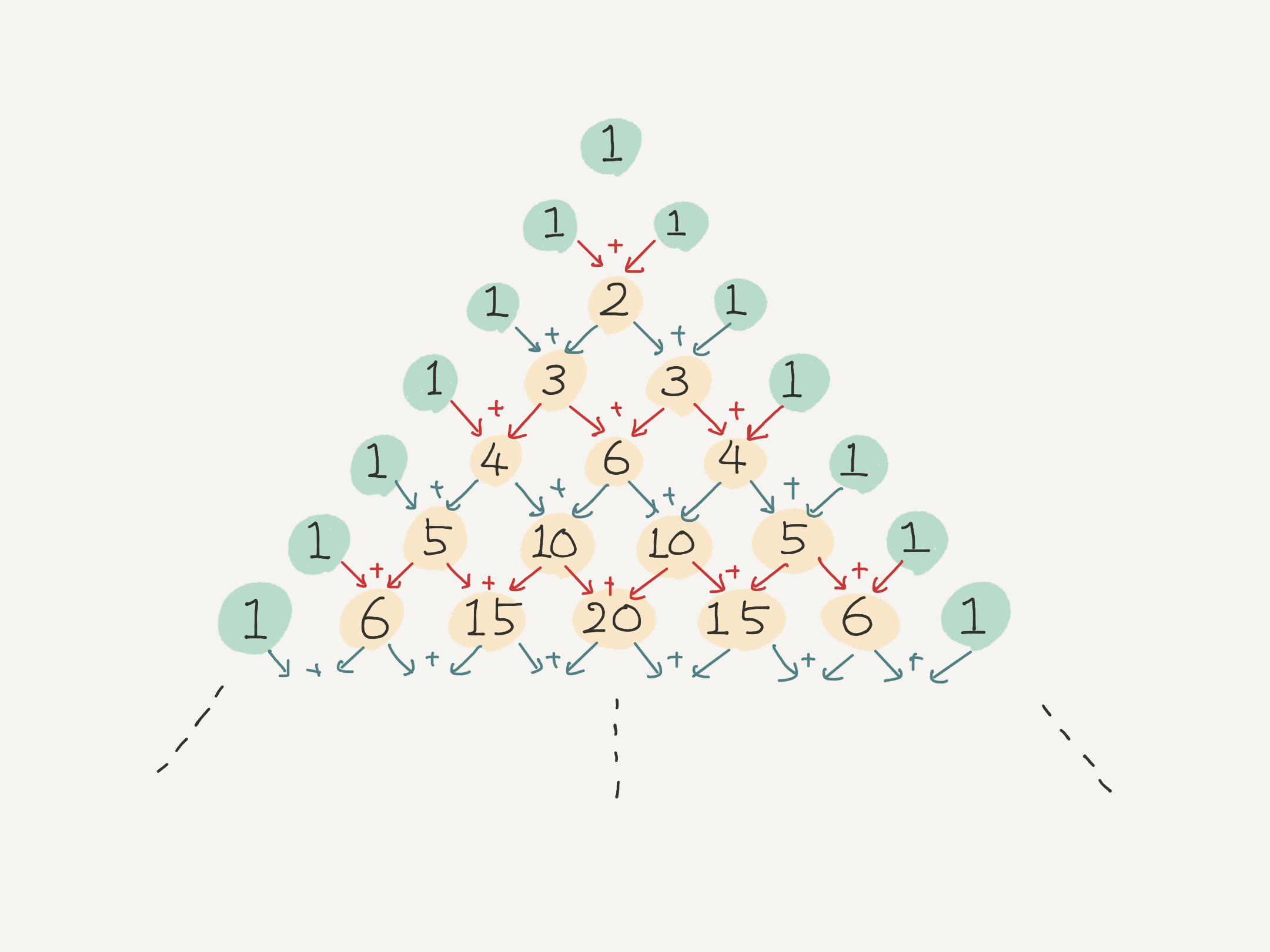
パスカルの三角形を書いていく様子(YouTube)
ユーリ「パスカルの三角形は、絶対に《できあがり》にはならないけどね」
僕「え?」
ユーリ「だって、ずっと続くんでしょ。だったらどこまで下に行っても終わらないじゃん?」
僕「まあそうだね。無限に続けていけるから、確かにパスカルの三角形をすべて書き上げることは不可能といえる。 でも、パスカルの三角形の各行をどんなふうに作っていくかははっきりしてる。 だから、どれだけ下の行を選んでも、そこにどんな数が並んでいるかはわかる——原理的には」
ユーリ「たとえば、 $12345$ 行目にどんな数が並ぶかとか、 $100$ 億行目にどんな数が並ぶかとか」
僕「そういうこと。 実際問題として、そこまでパスカルの三角形を書くことは難しいと思うけど、 その《難しさ》というのは、 時間がとんでもなく掛かるとか、そんなに書けるほど大きな紙がないといった難しさであって、 原理的にやり方がわからないという難しさじゃない」
ユーリ「ふむふむ。ごもっとも」
僕「ええと、それでパスカルの三角形がどうしたんだろう——ははあ、また例の彼氏と《数学対決》してるんだな、さては」
ユーリには、いつも《数学対決》しているボーイフレンドがいるのだ。
《数学対決》という謎の概念。
詳しくは知らないけど、 数学の問題を出し合って相手が解けるかどうかで勝負するんだろうな、たぶん。
16世紀のイタリアで数学の公開試合をやったみたいに。
※カッツ『数学の歴史』参照(p.408)。
ユーリ「んにゃ! あいつは関係ないの。それに彼氏じゃないし。ユーリは自主的研究中なのじゃ」
僕「おお! どんな研究?」
ユーリ「あのね、二つ足すだけなのに、どーして組み合わせの数になるの?」
僕「パスカルの三角形に出てくる数は、上の行の二つの数を足して作っている。 どうしてその作り方で《組み合わせの数》が出てくるのか——ユーリが考えているのはそういうこと?」
ときどきユーリは、説明が言葉足らずになることがある。だから僕は、彼女の言葉を補いつつ聞き返した。
ユーリ「うん。そゆこと。なんで?」
僕「それって、ユーリに教えたことあるよね。確か証明もしたような気がするけどな」
ユーリ「はいまた一点減点!」
僕「今度は何が減点対象なんだろう」
ユーリ「『それって教えたことあるよね。せっかくワシが教えたのに、覚えてないとはケシカラン!』なんて言うから減点」
僕「そんなこと言ってないからね」
ユーリ「でもさー『教えたことあるよね』って、そーゆー風に思っているみたいに聞こえるんだよー」
僕「今日はえらく突っかかってくるなあ」
ユーリ「突っかかるのは、お兄ちゃんを信頼してる証拠なのさ! 誰にでも突っかかるわけじゃないよん。 ……教えてくれたことあったかもしれないけど、忘れたんだもん!」
【CM】
テトラ「はい、ここでCMに入ります。 先輩がユーリちゃんにパスカルの三角形のお話をするようすは、 『場合の数』に出てきますね」
テトラ「それから、場合の数といえば確率。パスカルの三角形は『確率の冒険』にも出てきますよ!」
僕「うん、わかったわかった。 確かに、誰でも忘れることはある。 でもきっと考えればすぐに思い出すよ」
ユーリ「そっかなー」
僕「思い出さなくてもいいよ。もう一度、最初から一緒に考えていこうか。 いったんパスカルの三角形から離れて、 組み合わせの数の話をしよう」
ユーリ「うん! 組み合わせの数は知ってる!」
僕「ユーリは組み合わせの数は知ってる、と。じゃ、組み合わせの数について教えて」
ユーリ「たとえば、 $4$ 個のものから $2$ 個選ぶ組み合わせの数は、 $6$ 通りでしょ?」
僕「そうだね」
ユーリ「そーゆーこと!」
僕「いやいや、もうちょっと詳しく教えてほしいな。 $4$ 個のものから $2$ 個選ぶ組み合わせって、 たとえばどういうものなのか、具体的に話してほしいんだけど」
ユーリ「いーよん。たとえば $1,2,3,4$ の $4$ 個の数があるとするよね。 数字が書かれた紙が $4$ 枚あるみたいな状況……別に紙でなくてもいいけど、 とにかく $4$ 個の数がある」
$4$ 個の数がある
僕「うん。いいよ」
ユーリ「そんでね、その $4$ 個の数の中から $2$ 個を選ぶとする。 たとえば、 $1$ と $2$ を選ぶとか、 $1$ と $3$ を選ぶとかね。いろんな選び方があるわけじゃん?」
僕「そうだね」
ユーリ「あっ、そーだ。あのね、 $4$ 個のものから $2$ 個を選ぶんだけど、選ぶ順番はどーでもいいの」
僕「順番がどうでもいいというのは?」
ユーリ「$2$ と $3$ を選ぶのと、 $3$ と $2$ を選ぶのと同じってこと。 $2,3$ と $3,2$ は区別しない」
僕「なるほど。どういう順番で選んでも同じ選び方だと見なすってことだね」
ユーリ「そゆこと。そーやって $1,2$ とか $1,3$ とか $2,3$ とか……いろんな選び方がある。 その一つ一つが《$4$ 個から $2$ 個選ぶ組み合わせ》なんじゃよ」
$4$ 個から $2$ 個選ぶ組み合わせの例
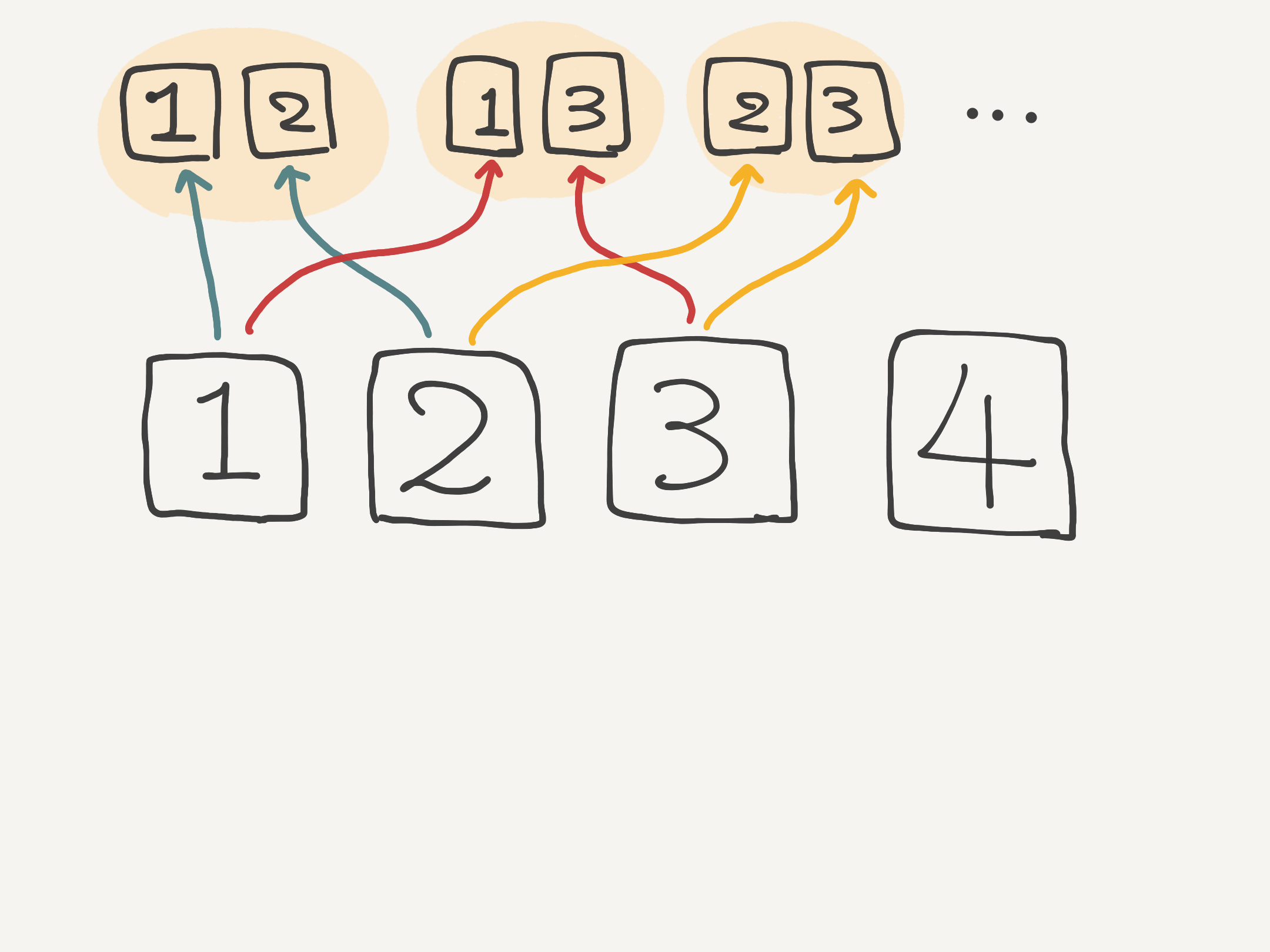
僕「うんうん、よくわかりましたよ。ユーリ先生。ところで、組み合わせを選ぶときは、 $1$ と $1$ を選んでもいいの?」
ユーリ「それはダメ。 $1,1$ とか、 $4,4$ みたいに同じものがだぶっちゃだめ」
僕「《$4$ 個から $2$ 個を選ぶ組み合わせ》といったときは異なる $2$ 個を選ぶ」
ユーリ「そーそー」
$4$ 個から $2$ 個選ぶ組み合わせでは、異なる $2$ 個を選ぶ
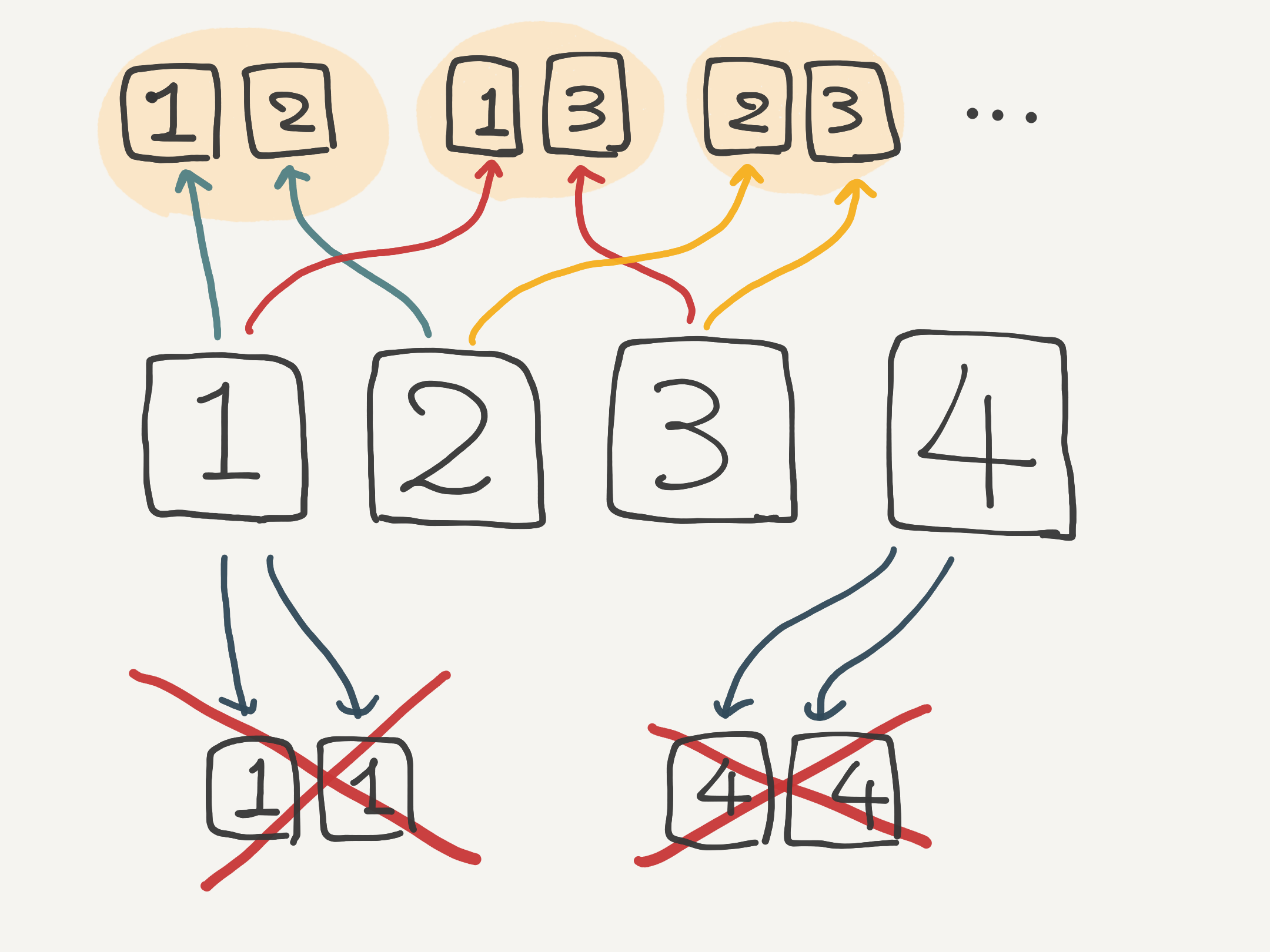
僕「$1,2,3,4$ の $4$ 個から、異なる $2$ 個を選ぶ。順番が違っていても同じ選び方だと見なして区別しない。 その $1,2$ や $1,3$ や $2,4$ という選び方の一つ一つが《$4$ 個のものから $2$ 個を選ぶ組み合わせ》なんだね」
ユーリ「うん。だから、 $1,2,3,4$ の $4$ 個から、 $2$ 個を選ぶ組み合わせは $6$ 通りでしょ?」
僕「その $6$ 通りある組み合わせは全部書ける?」
ユーリ「もちろん!」
$1,2,3,4$ という $4$ 個の数から $2$ 個を選ぶ組み合わせは $6$ 通りある
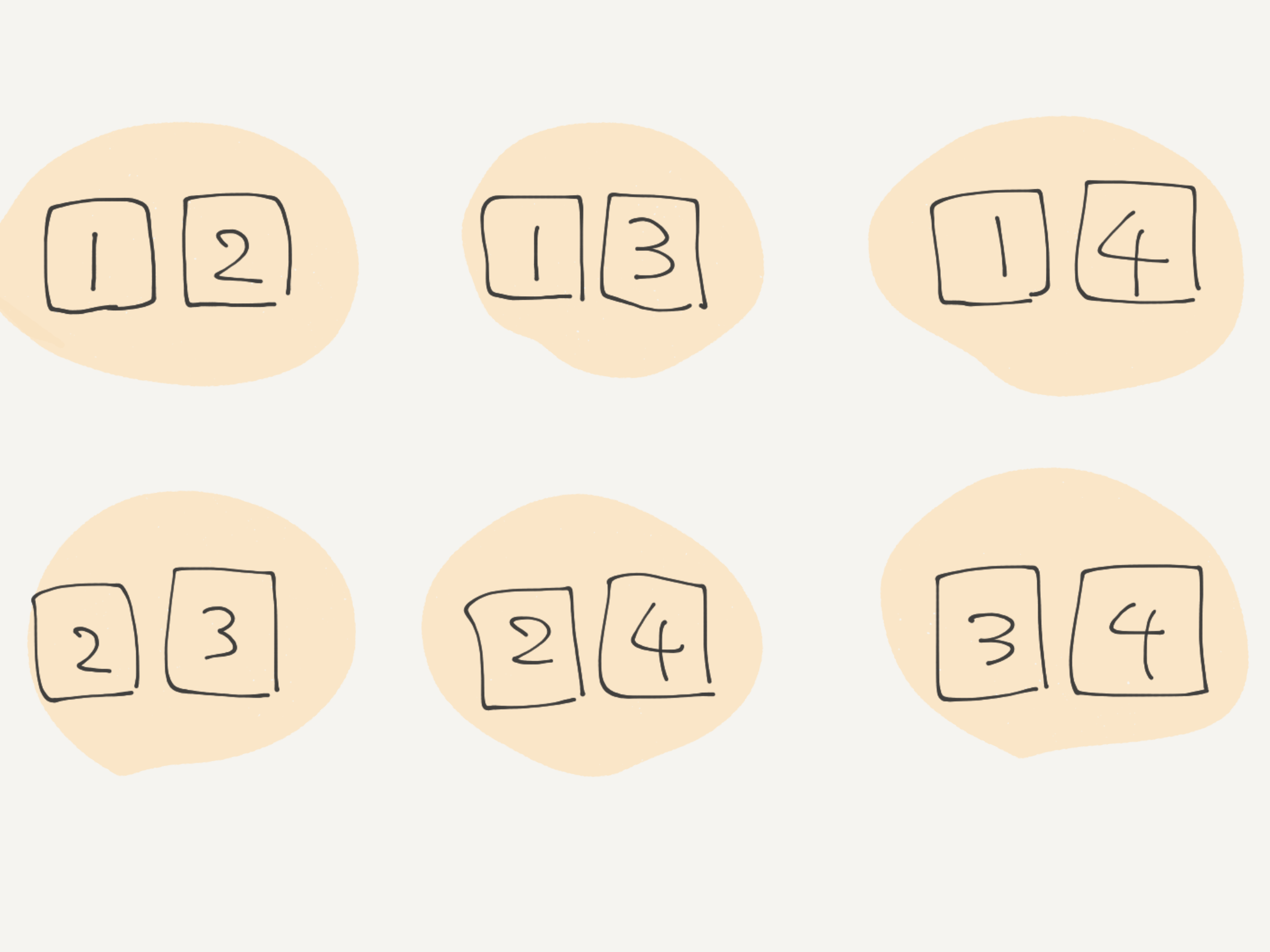
僕「なるほど。確かに $6$ 通りある。 $3,2$ が入っていないけど、大丈夫?」
ユーリ「だって、 $2,3$ があるもん。組み合わせは順番を考えないんだから、 $2,3$ と $3,2$ は同じ組み合わせでしょ。 $2,3$ と $3,2$ を両方入れたら二重に数えることになっちゃう」
僕「そうだね。ユーリは組み合わせの数のこと、ちゃんとわかってるね」
ユーリ「ふふん」
僕「そこまでわかってるんだったら、パスカルの三角形にどうして組み合わせの数が出てくるか、 すぐにわかると思うんだけどなあ……」
ユーリ「そーなの?」
僕「そうだよ。パスカルの三角形の作り方をもう一度なぞってみればよくわかる」
ユーリ「そーかにゃあ……」
僕「でもその前に、組み合わせについてもう少し聞いてもいい?」
ユーリ「どんとこい」
僕「ユーリはいま《$4$ 個から $2$ 個選ぶ組み合わせ》を $6$ 個全部書き上げたよね。 もしも誰かから『これで本当に全部の組み合わせを書き上げたの?』って言われたら何て答える?」
ユーリ「《$4$ 個から $2$ 個選ぶ組み合わせ》はこの $6$ 個以外にはないもん!……って答える。 $1,2$ と、 $1,3$ と、 $1,4$ と、 $2,3$ と、 $2,4$ と、 $3,4$ しかないでしょ?」
僕「そうだね。ユーリはすごく注意深くこの $6$ 個を書き上げている。 僕はこんなふうに読んだんだよ。 $1,2,3,4$ の $4$ 個から $2$ 個を選ぶ組み合わせを考えるとき——
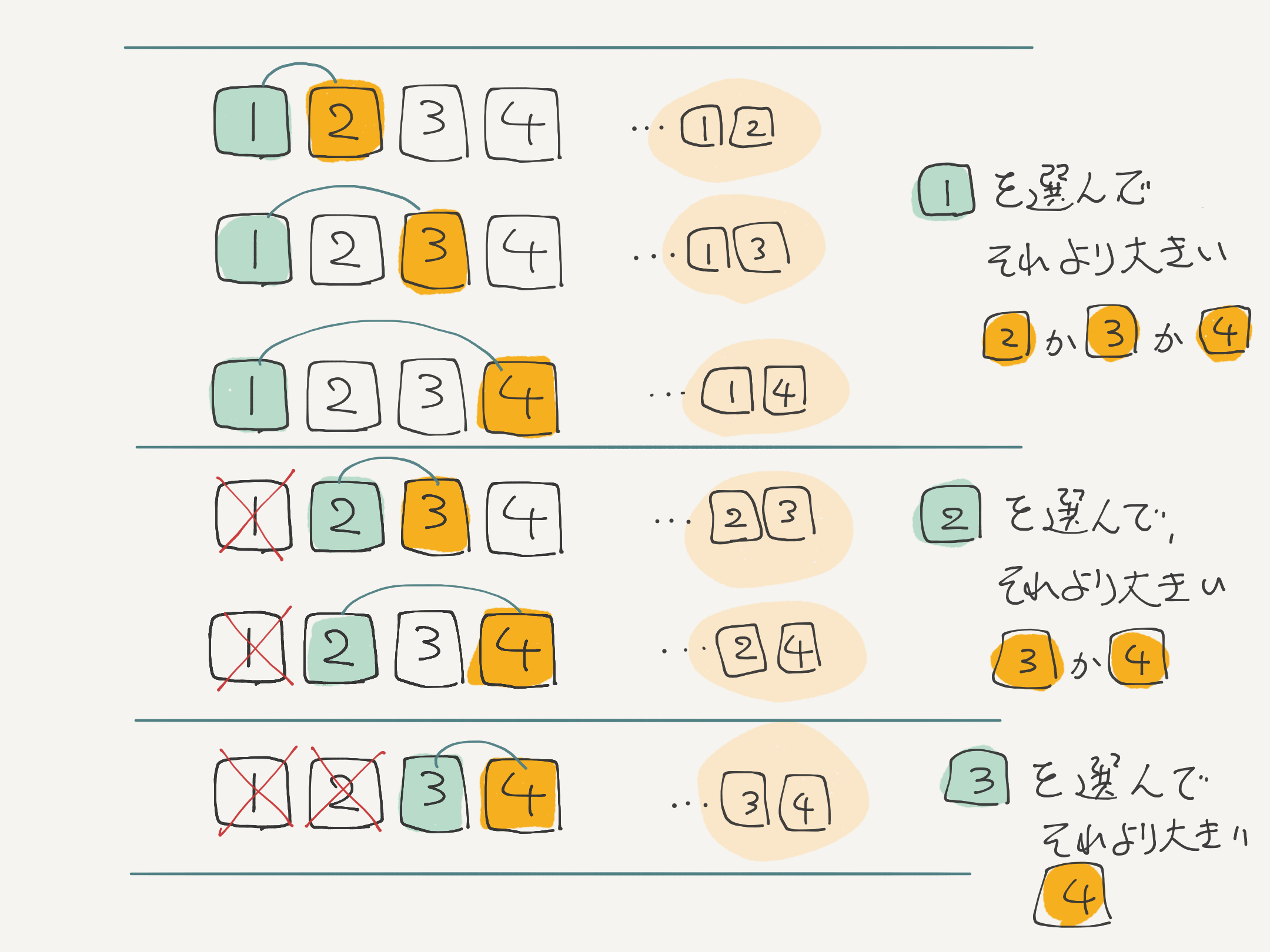
ユーリ「おー! そんなの、意識してなかったよー……でも、言われてみればそーかも!」
僕「ユーリが書き上げた組み合わせを見ていると、 $4$ 個の数 $1,2,3,4$ から $2$ 個の数の組み合わせ $x,y$ を選ぶときには、 必ず、 $$ x < y $$ という条件を満たすように選んでる。 $x < y$ という条件を付けることで、 $2,3$ と $3,2$ の両方をだぶって数える心配がない」
ユーリ「……」
僕「それから、 $x,y$ という組み合わせを並べるときには、 $x$ が小さい方を先に書いているし、 $x$ が等しい場合には $y$ が小さい方を先に書いている。 だから『ああ、すごく注意深く書いているな』と思ったんだ。 システマティックに列挙してるよね」
ユーリ「システマ何とか……ってどーゆー意味?」
僕「システマティックっていうのは、『系統立てている』という意味の英語だよ。 行き当たりばったりに書き並べたんじゃないってこと。 英和辞典で英単語がアルファベット順にならんでいるのと同じように、 組み合わせを列挙している」
ユーリ「いやー、全然意識してませんでしたぜ、ダンナ」
僕「誰がダンナだよ。 $6$ 個くらいならまだいいけど、 組み合わせを列挙していくときには、 システマティックに列挙しないとすぐに混乱してしまうから。 樹形図も、システマティックに考えるのにいいよね」
樹形図

ユーリ「樹形図は習ったよ。でもシステマティックって習ってない」
僕「システマティックに数えるっていうのは、このあいだテトラちゃんが言ってたんだ。 根気よく数えるために大事だって話だったかな。テトラちゃんはそういうのが好きなんだね」
ユーリ「テトラさん、言いそう」
僕「システマティックに数えたり、列挙したりする方法は他にもあるよ。たとえば……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第391回終わり)
(2023年5月19日)