第190回 シーズン19 エピソード10

数の謎、いにしえの謎

双倉図書館にて

ユーリ「お兄ちゃんもテトラさんも、早く早く！　たっくさんパネルがあるから、全部まわるのに時間足りなくなるよ！」

僕「そもそも、全部まわるなんて無理だって、ユーリ。 ミルカさんは古代バビロニアの方に行ったらしいから、そっちを見ようよ」

ユーリ「楔形文字（くさびがたもじ）は、さっき見たし……」

僕「古代バビロニアの部屋のパネル、全部は見てないよ」

テトラ「たくさんありましたものね」

古代バビロニアの部屋

ユーリ「あ、ミルカさまだ。パネルクイズを見てる！」

ユーリ「バビロニア……ってことは、六十進法？」

テトラ「そう書いてありますね」

僕「数の表ってことなのかな。ミルカさんはこのクイズを考えていたの？」

ミルカ「……」

ミルカ「……いや、私もいま見始めたところだよ」

ユーリ「六十進法だと、よくわかんない」

テトラ「いえ、じっと見ていると、わかることはありますね。 たとえば、いちばん右の第 $4$ 列を縦に読むと、 $1,2,3,\ldots,15$ と順番に数が並んでいます」

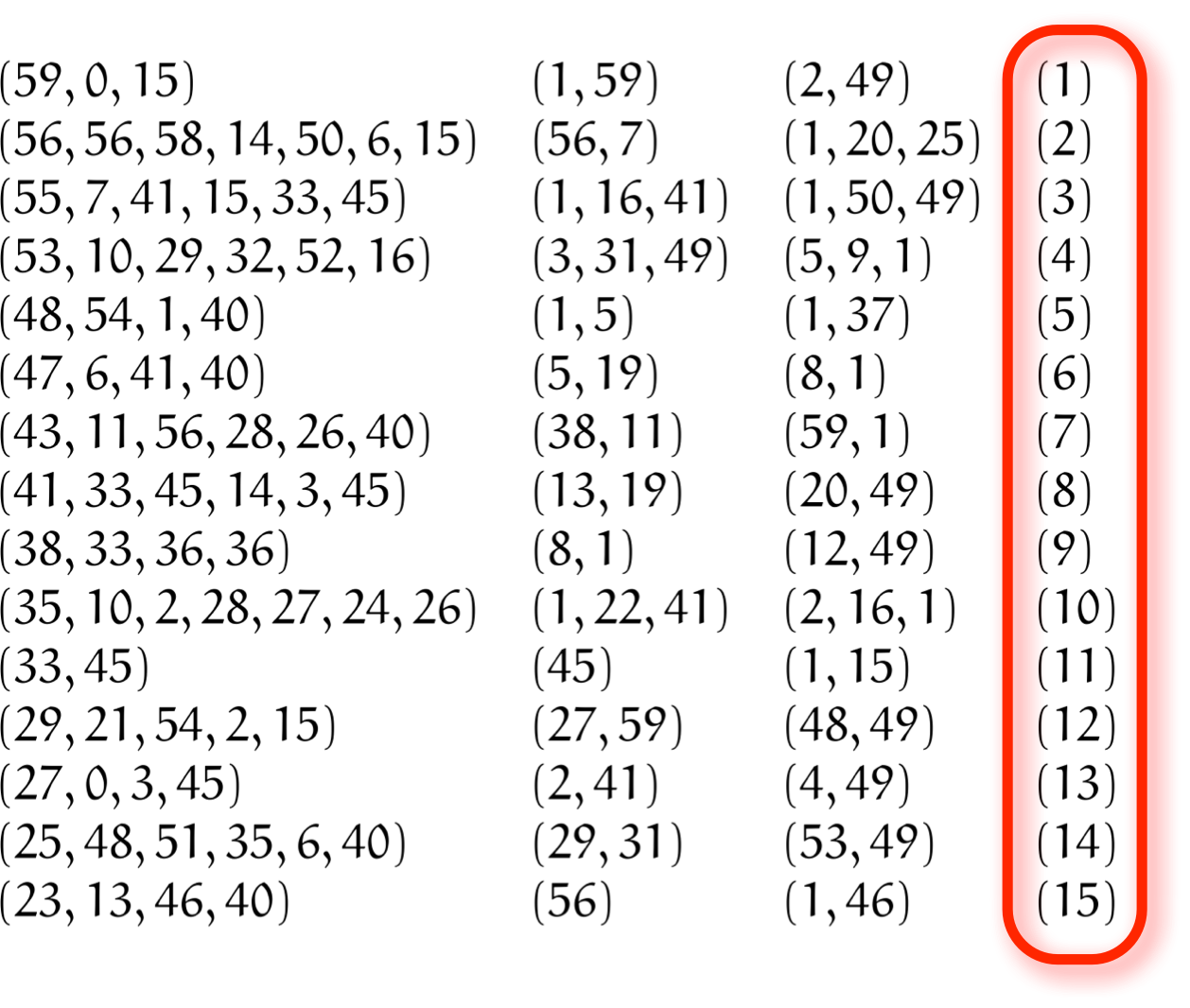
ユーリ「あ、そだね。六十進法だけど、各桁は十進法だから？ $0$ から $59$ までは十進法なんだよね」

僕「そうだったね」

ミルカ「他にもわかることはある。第 $1$ 列の最上位を縦方向に見てみると、 $59,56,55,\ldots,25,23$ のように大きい順に並んでいるように見える」

僕「確かに」

ミルカ「しかし、それ以上の観察はちょっと難しそうだ。リサはどこかにいないかな」

テトラ「リサちゃんは、さっき一瞬いましたけど」

リサ「《ちゃん》は不要」

テトラ「……って、いらしたんですね」

ミルカ「これを、十進法の位取り記数法に変換できる？」

リサ「可能」

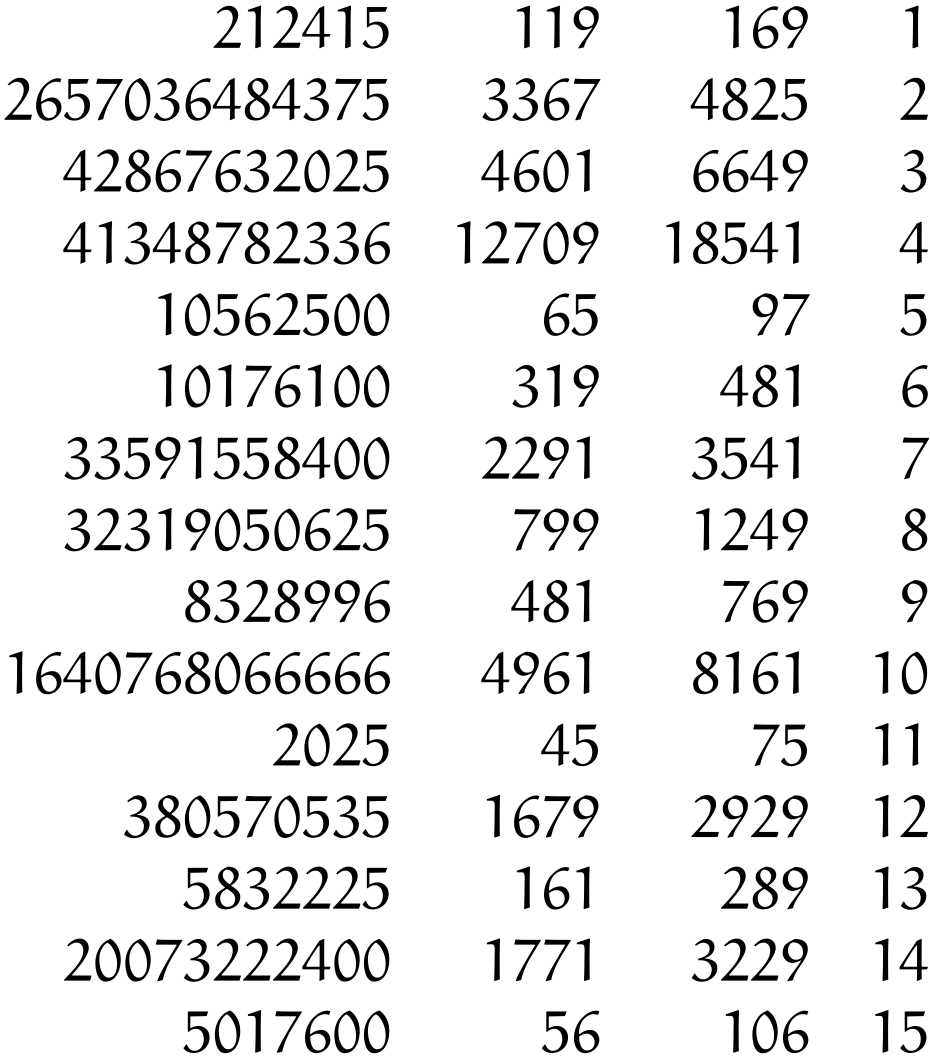
僕「うーん、ずいぶん眺めが変わるなあ」

ユーリ「第 $4$ 列は変わんないね。 $1,2,3,\ldots,15$ だから」

ミルカ「第 $1$ 列は極端に大きくなった」

テトラ「それに比べると、第 $2$ 列と第 $3$ 列は《だいたい同じくらいの大きさ》になっていますね。 たとえば、第 $1$ 行目は $119$ と $169$ で、およそ $100$ ですが、 第 $4$ 行目は $12709$ と $18541$ で、どちらもおよそ $10000$ です」

僕「確かに……」

ユーリ「シャキーン！　ユーリ、ひらめいちゃった！」

テトラ「なんでしょう」

ユーリ「あのね、数の列だから、これって数列じゃん？　数列ときたら階差数列をとってみなくちゃ！　たとえば、 この第 $2$ 列の階差数列！」

ユーリ「ありゃ？　めちゃめちゃ」

僕「うーん……これはちょっと違うんじゃないかな。 第 $2$ 列を縦に見ると、数十のものもあれば、一万超えるものもあるからなあ……」

ユーリ「そっか」

ミルカ「むしろ隣同士はどうだろう」

テトラ「あっ、あたしもそれをいま思っていました」

ユーリ「隣同士って？」

テトラ「あのですね。第 $2$ 列と第 $3$ 列はほぼ同じくらいの大きさの数じゃないですか。 これの差を求めてみるんですよ」

ユーリ「$119 - 169 = -50$ とか？」

テトラ「そうです」

ミルカ「リサに表の形にしてもらおう」

リサ「できてる」

僕「ああ、列に名前を付けたんだね、 $A,B,C,D,B-C$ って」

テトラ「これでは、 $B-C$ は全部マイナスになってしまいますね。 $B < C$ ですから」

リサ「$C - B$ に修正」

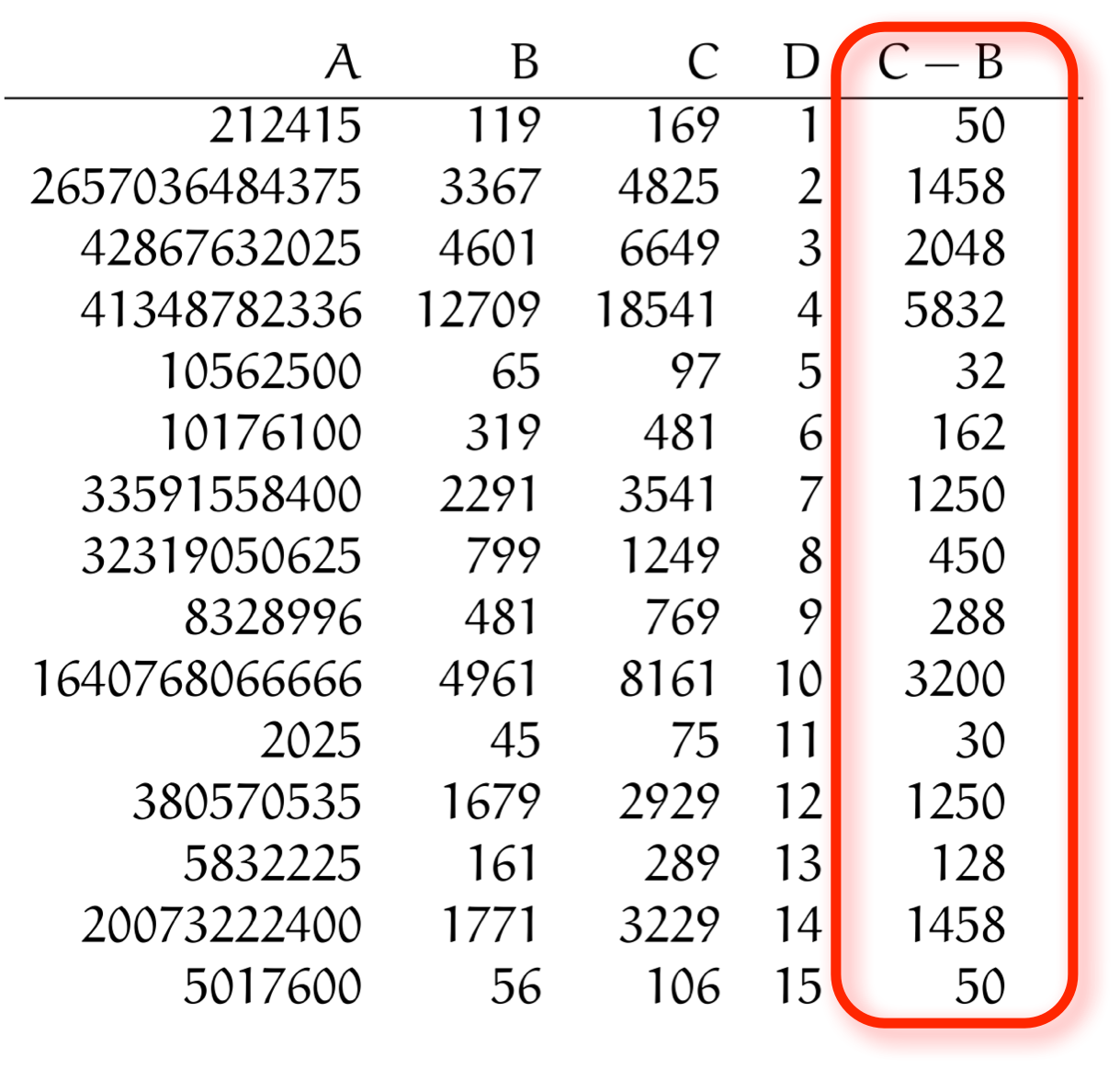
ユーリ「テトラさん、これも違うんじゃない？　 $50$ になったり、 $1458$ になったり……」

テトラ「それはそうなんですけど……」

ミルカ「$0$ か、 $2$ か、 $8$ になるのはなぜだろう」

テトラ「何の話ですか？」

ミルカ「$C - B$ をよく見る。一の位は必ず $0$ か $2$ か $8$ になっている」

ユーリ「$5\underline{0}, 145\underline{8}, 204\underline{8}, 583\underline{2}, \ldots$ ほんとだ、全部偶数！」

僕「でも、 $4$ や $6$ にはならない？」

テトラ「確かにそうですね」

僕「これは……」

ミルカ「これは、素因数分解したくなる」

リサ「$C - B$ の素因数分解」

ミルカ「なるほど」

ユーリ「？」

テトラ「？」

僕「うーん、 $C - B$ には、素因数が $2$ と $3$ と $5$ しか出てこないってこと？　たとえば、 $7$ も $11$ も出てこない」

テトラ「あっ、ほんとですね……でも、それは何を意味するんでしょうか」

ミルカ「私にもわからない。しかし、 $2,3,5$ は $60 = 2^2\times3\times5$ の素因数ではあるな」

僕「そうだ、 $C + B$ の素因数も同じじゃない？」

僕「ほらやっぱり！　 $C-B$ も $C+B$ も、素因数は $2,3,5$ だけなんだよ」

テトラ「でも、やっぱり……それが何を意味するか、あたしにはわかりません」

ミルカ「第 $11$ 行目はシンプルだな」

ユーリ「素数って、 $$ 2,3,5,7,11,\ldots $$ だよね……」

僕「六十進法に関連しているのかな……」

ユーリ「お兄ちゃん！　《逆数表》じゃない？」

僕「逆数表？」

ユーリ「ほら、バビロニアの《逆数表》には $7$ と $11$ がなかったじゃん？」

僕「うん、そうだったね。言い換えると、バビロニアの《逆数表》には $2,3,5$ を素因数に持つ数しか出てこない……か」

ミルカ「ふむ、なるほど。逆数が六十進法の有限小数で表記できる数になるということか」

テトラ「みなさん、ちょっとお待ちください。テトラは迷子になっています。 差を取ったり、和を取ったり、素因数分解したり、素因数の種類を調べたり……はいいのですが、 それで、 $B$ 列や $C$ 列はわかるんでしょうか」

ミルカ「わからないから、いろいろやってみるんだろう？　テトラ」

テトラ「そ、それはそうですね……」

僕「$C - B$ や $C + B$ は、素因数として $2,3,5$ 以外は持たない。 いいかえると、 $C - B$ も $C + B$ も、逆数を六十進法で表記したとき、有限小数で表記できる。 そして《逆数表》で逆数を計算しやすい数である……」

ユーリ「あれ？　素因数として $2,3,5$ 以外は持たないって、この表の数は全部そーなんじゃないの？」

僕「いや違うよ。たとえば $B$ 列の最初は、 $119 = 7\times17$ だから、 $7$ や $17$ という素因数が入ってる」

ユーリ「そっか……」

テトラ「$C - B$ と $C + B$ ばかり追ってていいんでしょうか。あまり先には進めないような気がするんですけれど」

ミルカ「いや。いま、二歩くらい進めたよ。ユーリが教えてくれた《逆数表》がヒントになった」

ユーリ「何がわかったんですか？」

ミルカ「リサ、 $C + B$ と $C - B$ を掛けてみると？」