![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
僕とユーリは双倉図書館(ならびくらとしょかん)で開催されているイベント《いにしえの数学》を見学中。
このイベントでは、さまざまな国の、古い時代の数学についてパネルが展示されている。
僕とユーリはバビロニアの数の表し方を学んだところ(第183回参照)。
バビロニアの記数法をそのまま使うと、 $3601$ と $61$ が紛らわしくなります。 そのため、アレクサンダー大王征服の時代までには、 空位を表す新しい記号が考案されました。
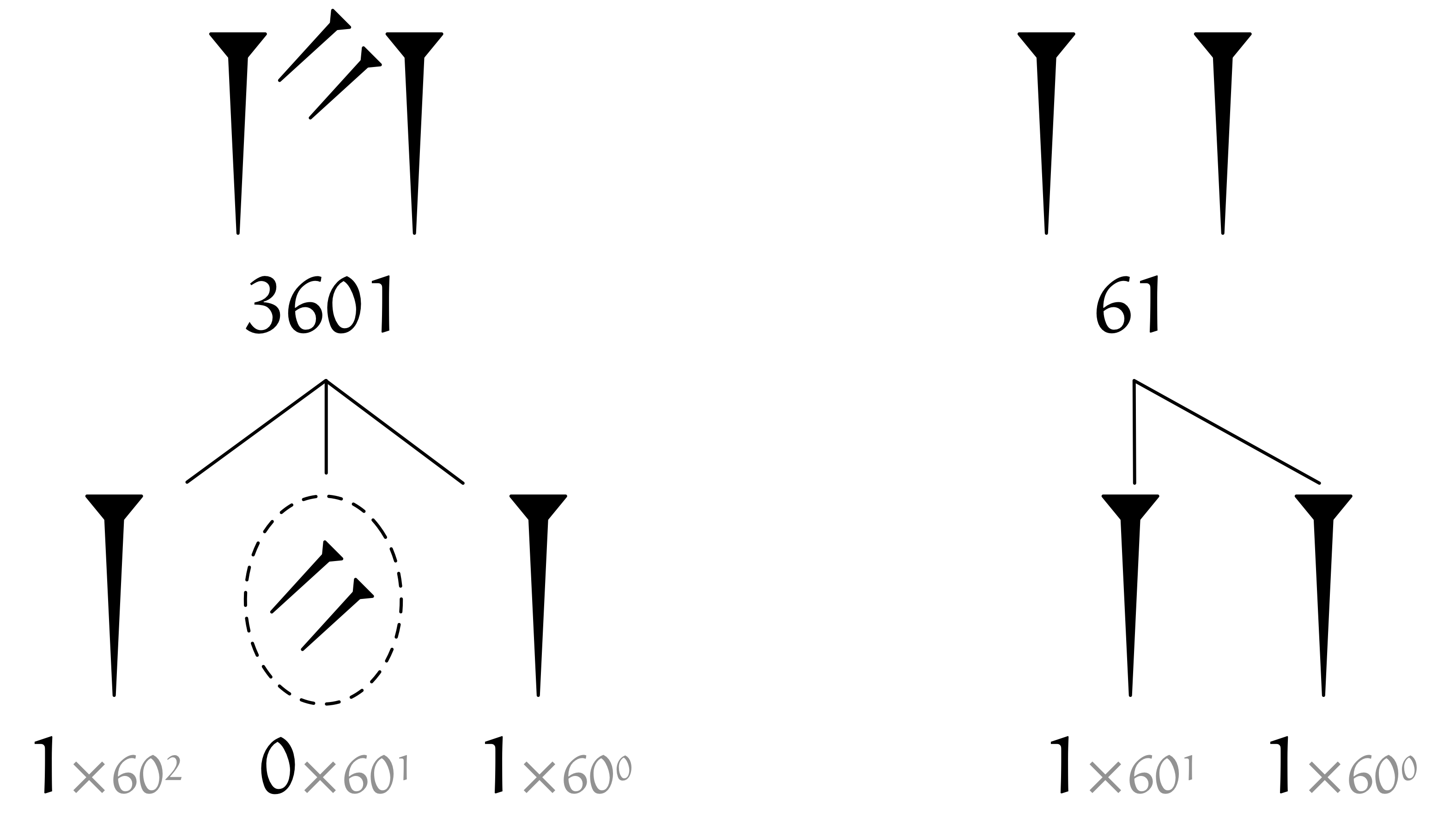
ただし、この記号は数字の末尾に使われることはありませんでした。
僕「なるほどね……ちゃんと対処されたんだ」
ユーリ「対処されてないじゃん! 数字の末尾に使われないんでしょ? だったら、やっぱり、 $1$ と $60$ は区別つかない!」
バビロニアの記数法、 $1$ と $60$

僕「確かに。 $1=1\times60^0$ と $60=1\times60^1+0\times60^0$ の区別が付かないな。 うーん、どうするんだろう」
ユーリ「パネルに解説ついてるみたい」
僕「なになに……『適切なスケールファクタ、 すなわち $60$ の冪指数は、文脈によって補うことになっており、 たとえば $2, 120, 7200, \frac1{30}$ などが、どれも同じ表記になっていた』そうだよ。 クヌース『The Art of Computer Programming Vol.2』より、と」
ユーリ「なにそれひどい! それで複雑な問題解けるの? 足し算とか掛け算とかめちゃくちゃになるじゃん!」
僕「いや、そうでもないんじゃないかな。二つの数を足すときには両方の桁が《そろっている》ことが大事だよね。 桁をずらして足しちゃまずいけど、そろっていれば大丈夫」
ユーリ「ちょっと待ってよー。だって、バビロニアだと $1$ と $60$ が同じなんだよ? だったら、 同じもの同士を足して $1+1=2$ と $60+60=120$ が同じなの? $2$ と $120$ が同じ?」
僕「同じだね。さっきの解説にも書いてあった。 $2,120,7200,\frac1{30}$ は同じ表記だって」
ユーリ「む……そっか、 $2, 120, 7200, \frac1{30}$ ってゆーのは、 $60$ 倍や $60$ 分の $1$ を繰り返したってことか……」
僕「そうだね。ほら、僕たちだって似たようなことやるよ」
ユーリ「やんないよー」
僕「やるって。たとえば、 $3000$ と $4000$ を足すとき、 両方のスケールファクタが $1000$ で同じだから、 $3+4=7$ という計算をして $7000$ という答えを出すよね。 $3+4=7$ の計算をするときには $1000$ をいったん忘れていたわけだ。 両方のスケールファクタがそろっているなら、うまく計算できる。 もちろん最後に実際のスケールファクタを思い出さなくちゃいけないけどね」
ユーリ「掛け算も?」
僕「うん、そうだね。僕たちが $1.23 \times 4.5$ のような掛け算をするときのことを考えればわかるよ。 いったん小数点のことを忘れて筆算をして、 最後に正しい位置に小数点をつけるよね。 だから掛け算途中では、 $123\times45$ なのか、 $1.23\times4.5$ なのか、 $12.3\times0.45$ なのかは気にしてないはず」
いったん小数点のことを忘れて筆算する
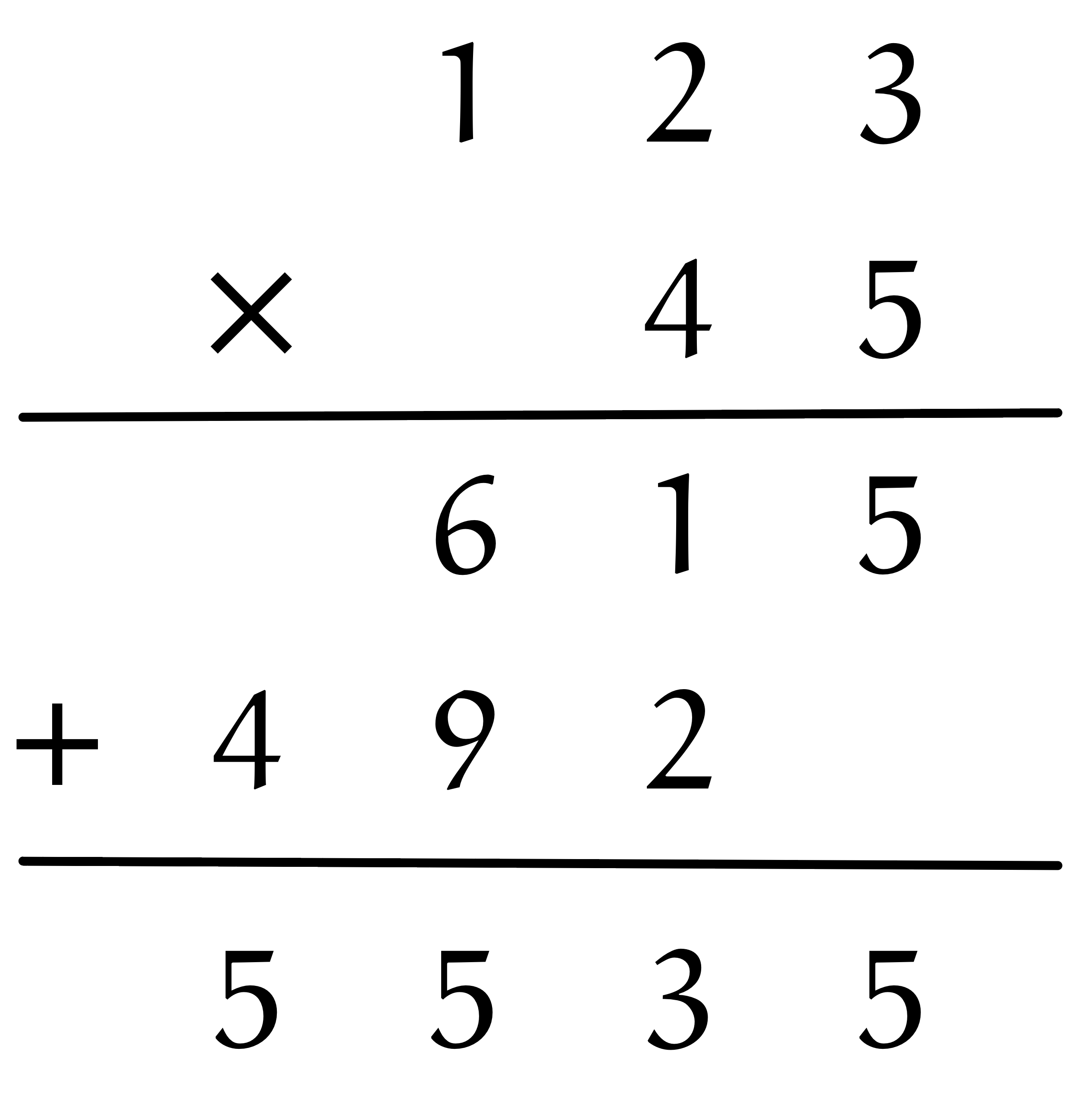
あとから正しい位置に小数点をつける
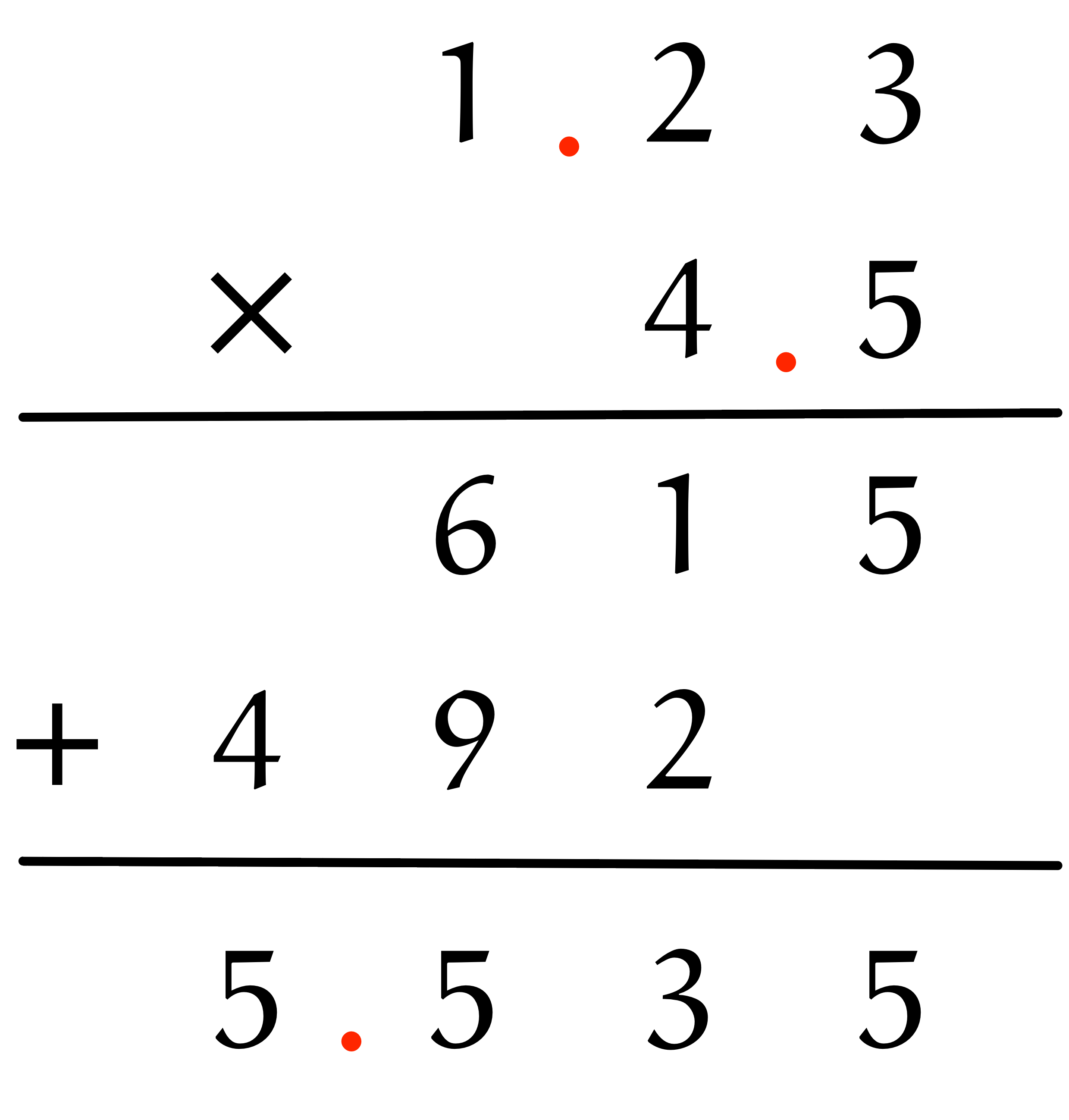
ユーリ「むー……確かにそーだけど」
僕「そろそろ、次のパネルに行ってみよう」
ユーリ「あ、クイズっぽいよ」
クイズ
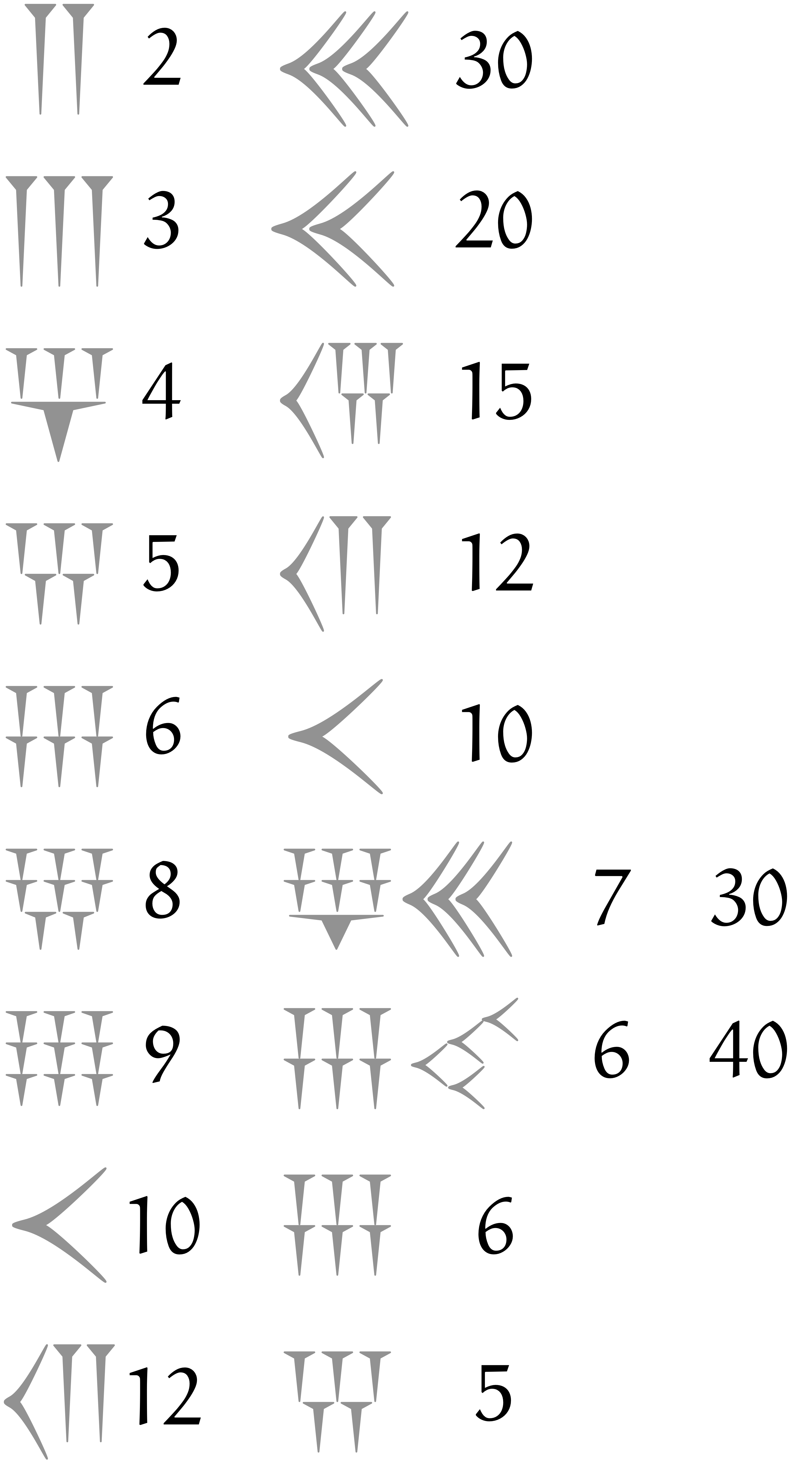
これはバビロニア人が計算で利用した数表の一部です。 いったい何の数表でしょうか。

僕「これは……」
ユーリ「またまた暗号解読!」

僕「まずは、僕たちの表記に直さないと」
ユーリ「まかせた」
僕「おいおい」
ユーリ「にゃるほど……わかったよん」
僕「早いな」
ユーリ「ユーリさまをナメないでよー。だって《$2$ と $30$》《$3$ と $20$》《$4$ と $15$》《$5$ と $12$》と見てきたら、 すぐにわかるもん。これって、《掛けたら $60$ になる数表》ってことでしょ?」
$$ \begin{align*} 2 \times 30 &= 60 \\ 3 \times 20 &= 60 \\ 4 \times 15 &= 60 \\ 5 \times 12 &= 60 \\ \end{align*} $$僕「うーん……僕もそう思ったんだけど……」
ユーリ「ぜんぶそーなってるもん! 《$6$ と $10$》も掛けたら $60$ だし、 $8$ と……あれ? $730$ ?」
僕「いや、 $730$ じゃないよ。ほら、バビロニアは《六十進法》なんだから、上の位の $7$ は $60$ 倍しないと、 $(7,30)_{60} = 7 \times 60 + 30 = 450$ ということだね」
ユーリ「$450$ でもだめじゃん。《掛けたら $60$ になる数表》だと思ったのになー! $8$ と $450$ 掛けても $60$ にならない……」
僕「掛けたらどうなるだろう」
$$ 8 \times 450 = 3600 $$ユーリ「$3600$ ……って、 $60\times60$ だよね?」
僕「そうか、この数表は《掛けたら $60$ になる数表》じゃない。《掛けたら $60^n$ になる数表》なんだ!」
ユーリ「えー? じゃ、次の試してみる。 $9$ と $6,40$ でしょ。 $(6,40)_{60} = 6 \times 60 + 40 = 400$ になる。 それで、 $9\times400$ を計算すると……」
$$ 9 \times 400 = 3600 $$僕「ほらね? $3600=60^2$ になった。やっぱり $60^n$ になる」
ユーリ「へー! 表の残りにある組は、掛けると $60$ になるよ。《$10$ と $6$》と《$12$ と $5$》だから。 このクイズの答えは《掛けると $60$ や $3600$ になる数表》じゃないの? お兄ちゃんは $60^n$ だっていったけど、 結局 $60$ と $3600$ しかないじゃん? 一般化しすぎだよー」
僕「そうかな……」
ユーリ「でも、なんで《掛けると $60$ や $3600$ になる数表》がいるんだろ? 計算に使ったって書いてあるけど」
僕「わかった! わかったよ、ユーリ。僕たちはバビロニアの気持ちになってなかった。 ユーリがいったように $1$ と $60$ は同じ書き方なんだ。だから、なるほどなあ!」
ユーリ「どーどー。ひとりで興奮しないで」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2017年2月3日)