![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕：数学が好きな高校生。
ユーリ：僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
テトラちゃん：僕の後輩。好奇心旺盛で根気強い《元気少女》。
リサ：自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
双倉図書館（ならびくらとしょかん）で開催されているイベント《いにしえの数学》では、 さまざまな国の、古い時代の数学についてパネルが展示されている。
テトラちゃんと合流できた僕とユーリは、 黄金比の研究に夢中になっていたけれど……
ユーリ「黄金比っておもしろいねー！（第187回参照）」
僕「そうだね！」
テトラ「ところで、先輩とユーリちゃんはもう《いにしえの数学》を全部ごらんになったんですか？」
僕「僕たちが回ったのは、 《古代エジプト》に、《バビロニア》に、それから《古代ギリシア》かな。 とても全部は回りきれないよね」
ユーリ「楔形文字で $\SQRT2$ の謎解きしたよ！（第184回参照）」
テトラ「順番はちがいますけど、 あたしもそっちは回りました。 あっちの《古代中国》に行きませんか？」
僕たち三人は、《古代中国》の部屋へ入っていった。
ユーリ「最初のパネルは、これ？」
テトラ「そうみたいですね。『中国文明は5000年以上さかのぼるという伝説があるものの、 この文明の確実な証拠で最も古いものは、黄河近くの安陽の発掘によるもので、紀元前1600年頃にさかのぼる』だそうです。 カッツ『数学の歴史』より」
僕「世界史に出てくるね。夏（か）、殷（いん）、周（しゅう）、春秋戦国時代、秦（しん）、漢（かん）……って時代を暗記したよ」
テトラ「パネルには、秦の始皇帝の話も書かれています。 『始皇帝は厳しい法律を強制し、均等税を賦課し、度量衡と貨幣、とりわけ文字の標準化を要求した。 また、始皇帝は反対者を弾圧するために古代から伝わるすべての書物を焼けと命じたと伝説は伝え……』」
ユーリ「えーっ！ 本を焼いちゃうの？」
僕「焚書坑儒（ふんしょこうじゅ）だね」
テトラ「『……と伝説は伝えるが（焚書坑儒）、この命令が実行に移されたか疑うべき理由もある』とありますね」
僕「へえ」
ユーリ「どーして、本を焼いたりするんだろ。 古代ギリシアでも記録がなくなっただの、紛失しただの、 あったよね（第185回参照）」
僕「そうだね」
テトラ「『始皇帝が紀元前210年に死去すると、秦王朝はすぐに倒れ、漢王朝がとって代わった。漢はその後約400年間続く』だそうです。 こちらもカッツ『世界の歴史』より。漢王朝は紀元前206年から紀元後220年までですね」
ユーリ「もしかして、『漢字』の『漢』って『漢王朝』のこと？」
僕「『漢』は『中国』の意味で使うことがあるよね。『漢語』とかも」
ユーリ「まーいーや。パネルクイズはないかにゃ？」
テトラ「あ、こちらには、漢王朝での数学の話が出てきましたよ。『漢は文官制度の確立を完成したが、 この文官制度を作り出すには教育制度が必要であった』なるほどです。 『この目的のために使われたテキストの中には、おそらく漢王朝初期に編纂された二つの数学書があった。 一つは『周髀算経（しゅうひさんけい）』で、もう一つは『九章算術（きゅうしょうさんじゅつ）』である』とのこと」
僕「なるほどね。教育のために数学のテキストをまとめたってことか」
テトラ「そのようですね」
ユーリ「ねーねー、あっちのパネルに行こーよ。クイズっぽいよ」
算木（さんぎ）
『九章算術』は漢王朝の時代に編纂された。中国最古ではないが、重要な古典である。 『九章算術』は紀元後3世紀の劉徽（りゅうき）など、多くの人の注釈で補充されてきた。
当時の中国では、算木を使って計算をおこなった。
算木は竹の棒で、大きさはさまざまだが、たとえば直径 $2.5$ mmで長さが $10$ 〜 $25$ cmのものがある。
$473$ という数は、算木で以下のように表すことができる。
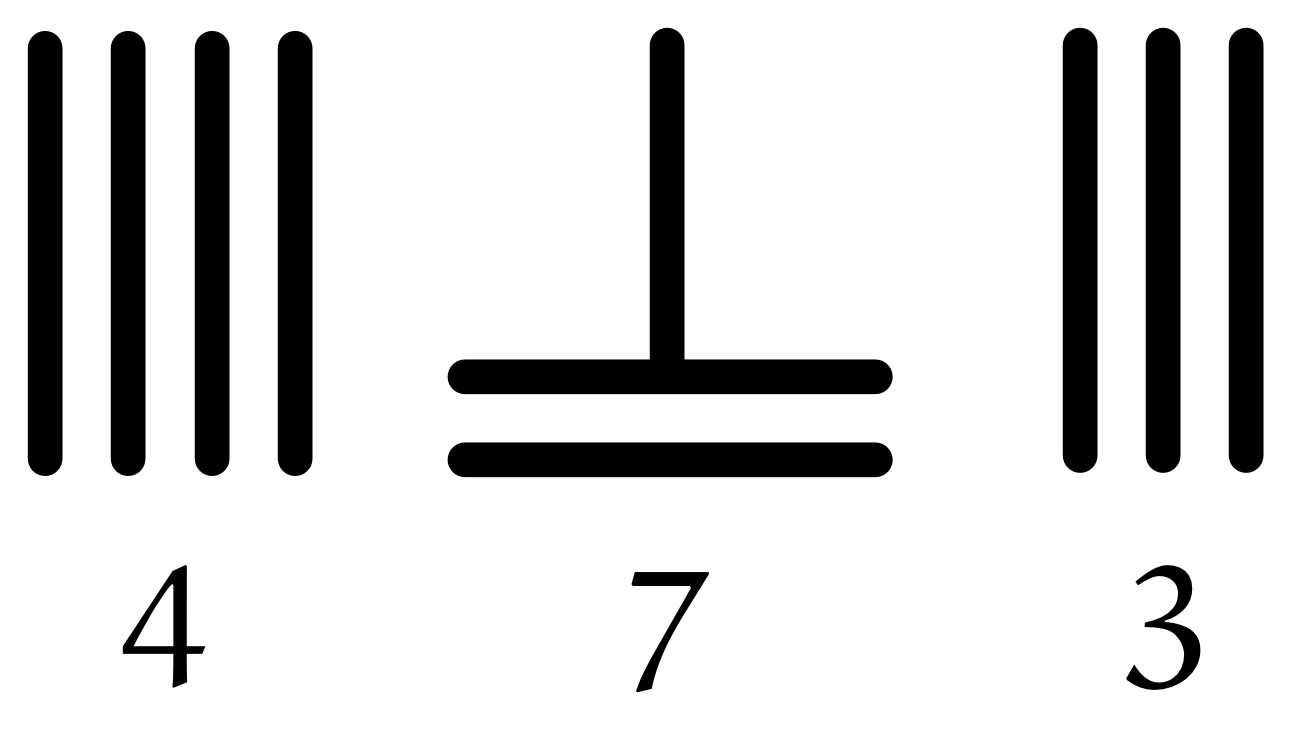
ユーリ「算木って、数字そのまんまだね。三本で $3$ 、四本で $4$ 。 $7$ は……これは $5+2$ ってことかにゃ？」
テトラ「こっちにクイズがありますよ」
クイズ（算木の色）
算木には《赤》と《黒》の二種類があった。 色の区別は何に使われたか。 想像しよう。
ユーリ「これはわかる！」
テトラ「わかりました」
僕「僕もわかったよ」
ユーリ「んじゃ、せーので答え合わせしよ？ せーの！」
テトラ「正負を表す？」
僕「正負の区別」
ユーリ「プラスとマイナス！」
クイズの答え（算木の色）
《赤》の算木は正の数を表し、 《黒》の算木は負の数を表した。 （『九章算術』の「正負術」より）
その他に、 末位の数に算木を斜めに重ねておいて負の数を表す場合もあった。
ユーリ「正解ですな！」
僕「こっちにもクイズがあるよ」
クイズ（算木の並べ方）
算木で数を表すときには、以下のような並べ方を使ったが、 並べ方には《縦式》と《横式》の二通りがあった。
《縦式》
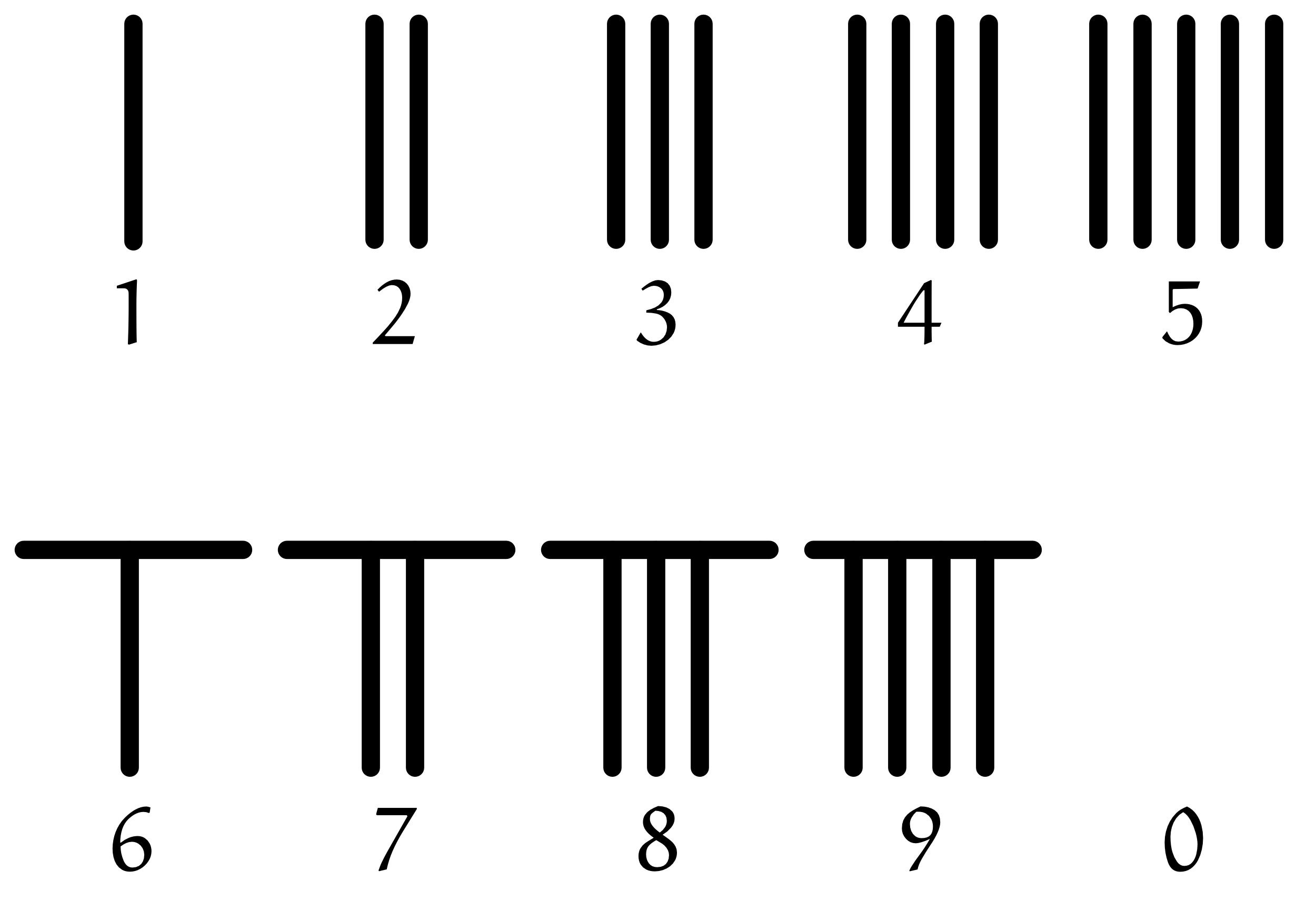
《横式》
並べ方に《縦式》と《横式》の二種類があるのは、何のためか。 想像しよう。
ユーリ「はあ？ また二種類あるの？ これもプラマイ？」
テトラ「いったい何のために、数が二種類も必要なんでしょう」
僕「いやいや、さっきヒントが出てたぞ……」
ユーリ「ヒントなんて出てたっけ。じょじゅちゅ、じょずつとりっく？」
僕「叙述トリックじゃなくてね」
ユーリ「わかんにゃい……」
テトラ「もしかして、ヒエログリフとヒエラティックのように、 使う人が違うとか？ 身分が高い人は《縦式》しか使わないみたいに」
僕「なるほど。それは古代エジプトの文字の話だね。 でも、僕はもっと簡単な話だと思う」
ユーリ「お兄ちゃんの答えは？」
僕「さっきのパネルに $473$ の例が出ていたよね。 あそこで、 $4$ と $3$ は、算木が《縦式》だったけど、 $7$ だけは《横式》だったんだよ」
算木で表した $473$
ユーリ「ほんとだ！」
テトラ「気付きませんでした……」
僕「だから、算木では《縦式》と《横式》を交互に使うんじゃないかな！」
ユーリ「なーるほど……って、 なんでわざわざそんな《めんどい》ことすんの？」
僕「……」
テトラ「……答えのパネル、見ましょうか」
クイズの答え（算木の並べ方）
算木で数を表すときには、以下のような並べ方を使ったが、 並べ方には《縦式》と《横式》の二通りがあった。
《縦式》
《横式》
一の位、百の位、万の位、百万の位……は《縦式》にする。
十の位、千の位、十万の位、千万の位……は《横式》にする。
つまり、一の位から《縦式》と《横式》を交互に使うので、 《$10$ の偶数乗》の位では《縦式》で、 《$10$ の奇数乗》の位では《横式》になる。
これによって、 $0$ を表す《空位》の有無がより明確になり、 誤りを減らすことができる。
たとえば、 $473, 4730, 4703, 4073, 40703$ はそれぞれ以下の通りになる。
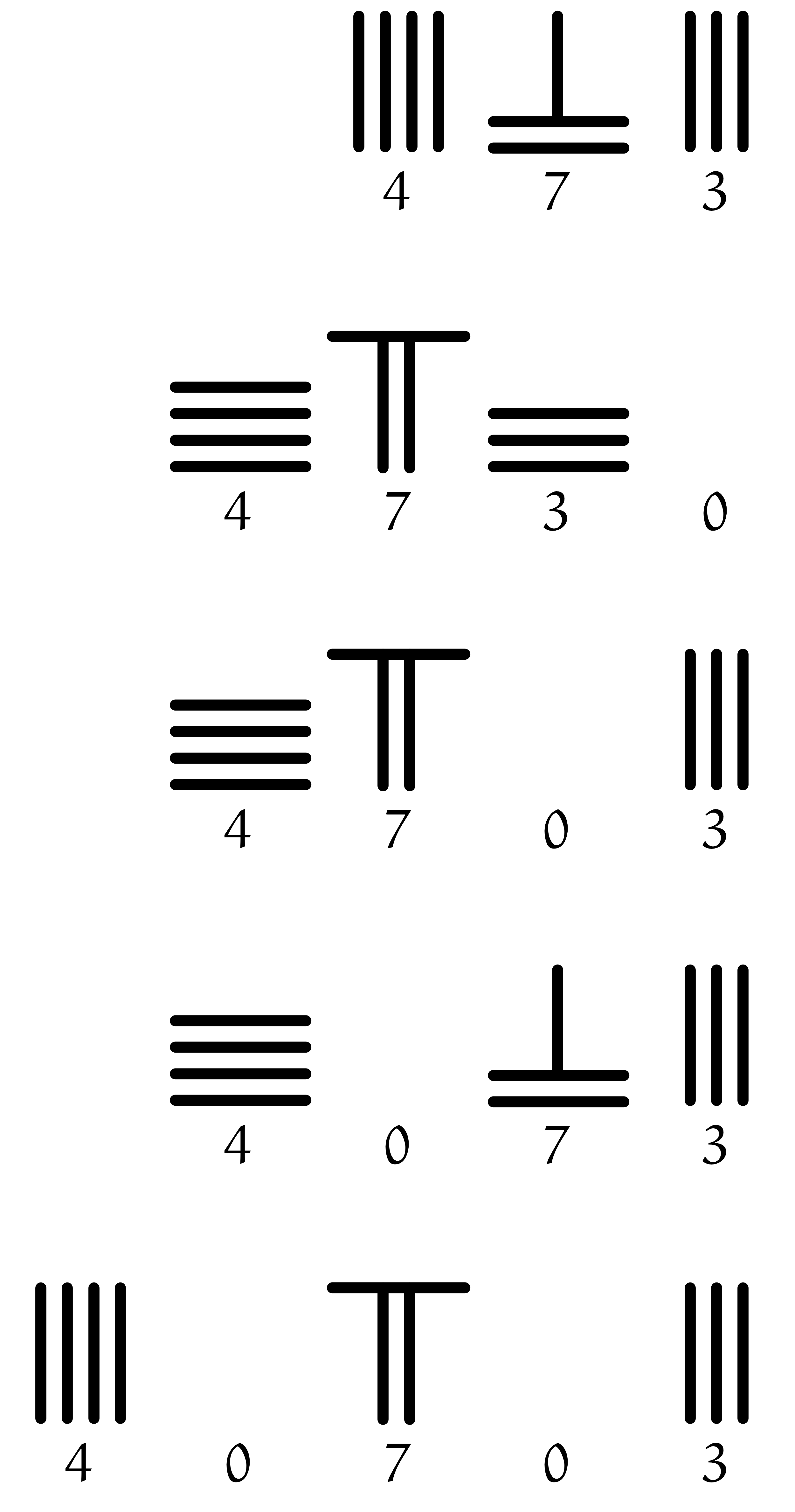
僕「なるほど！ 《縦式》と《横式》を交互にするルールにしておくと、 $0$ がどこにあるかわかりやすくなるんだね。たとえば、 $473$ と $4730$ は全然違う形になる」
テトラ「なるほどです。 十一万二千二百三十三（$112233$）はこうなりますね」
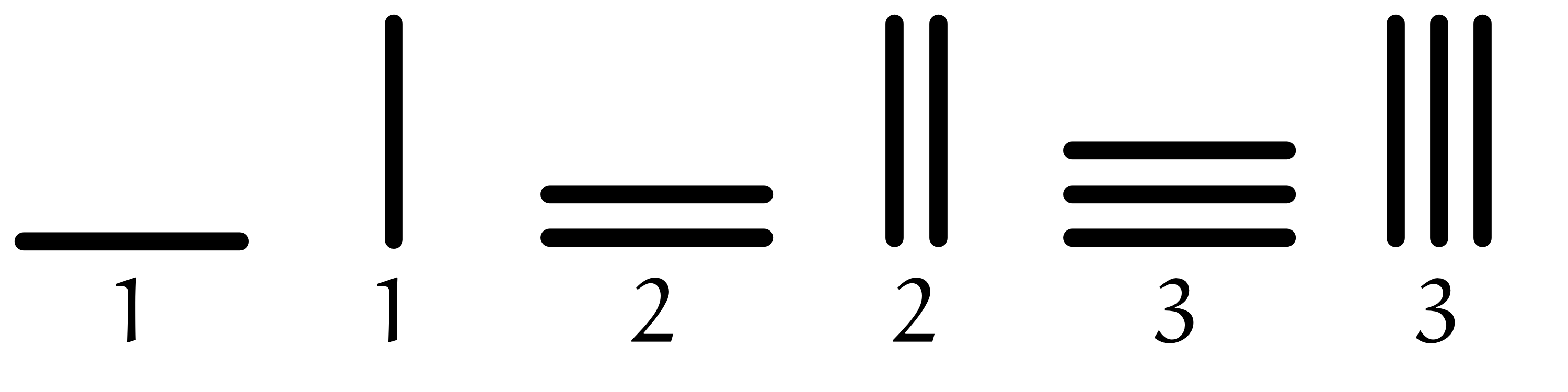
ユーリ「なるほどにゃあ！」
リサ「エラーチェック重要」
真っ赤なノートブック・コンピュータを抱えたリサが、 パネルに見入っている僕たちの後ろを早足で通り過ぎていった。
僕「うわっ」
ユーリ「もう行っちゃった……」
テトラ「こちらのパネルには『九章算術』についてもう少し詳しくあります」
『九章算術』
古代中国の数学書『九章算術』は、内容ごとに九つの章に分かれており、 二百問以上の問題が、問い・答え・解説の形式で書かれている。
『九章算術』の章ごとの内容は、以下の通り。
ユーリ「へー、いろんな問題が出てるんだ」
テトラ「平方根や立方根……それも算木で計算するんですか！」
僕「こっちにクイズパネルがある。これは乗算だね」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2017年3月3日）
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)