![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
『群論への第一歩』がすぐに《Web立ち読み》できます!
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕たちは、ユーリが持ち込んできた《格子点の世界》における《円》を議論していた(第411回参照)。
僕「距離なんだよ」
ユーリ「きょり?」
僕「僕たちは《平面の世界》で考えている距離という概念を、《格子点の世界》に移した。 それによって、《平面の世界》にある円が自然と《格子点の世界》の《円》に移ったんだ。 だから、 距離という概念は《平面の世界》と《格子点の世界》を行き来する《パスポート》のようなものなんだ!」
ユーリ「……」
僕「何を言ってるかわかる?」
ユーリ「うーん……わかるような、わからないような」
僕「円の定義を思い出せばわかるよ」
ユーリ「平面上で、一点から等距離にある点全体の集合。 ああ、等距離ってところ?」
僕「そう、そうなんだ。 《格子点の世界》での距離が定義できたから、 《半径》という概念を持ち込むことができて、 それで《円》という概念を持ち込むことができたといえる」
ユーリ「うん、それはわかる。だからこれは《円》になるんでしょ? 《中心》から $3$ 歩で行ける点の集まりだから」
《格子点の世界》における《半径》が $3$ 歩の《円》

僕「そういうこと。 ということは、距離を使って定義されている図形ならば、 円以外の図形も《格子点の世界》に持ってくることができることになる!」
ユーリ「距離を使って定義されてる図形……って、円以外にある?」
僕「もちろんあるよ。たとえば楕円だね」
楕円
ユーリ「楕円って、円をつぶした形だよね……距離って?」
僕「楕円の描き方を思い出せばわかるよ。手で楕円を描くときのこと」
ユーリ「楕円の描き方?……あ! 二本のピンに糸を張る奴! 思い出した!」
僕「そうだね。平面上で、固定した二点からの距離の和が一定の点全体の集合。それは楕円になる。
ユーリ「そかそか。格子点を二つ決めて、同じことやればいいんだね!」
僕「うん。距離は歩数で考える。 つまり、二点を $A$ と $B$ にすれば、 $A$ から歩いて《楕円》上の点まで行って、 そこから戻って $B$ まで来たときに一定の歩数になればいい」
ユーリ「行って戻る……それでうまく描ける?」
ユーリは空中で指を動かしながら首を傾げる。
きっと、彼女の目にはたくさんの格子点が浮かんでいるんだろうな。
僕「ええと、そうだなあ。 $A$ から行って $B$ に戻るんじゃない方がいいかな。 $A$ から $a$ 歩の点をぜんぶ描きあげて、 $B$ から $b$ 歩の点をぜんぶ描きあげて、 両方の共通部分を考えた方がいいかも。 つまり、二つの《円》を描くわけだ。《半径》が $a$ と $b$ の《円》だね」
ユーリ「二つの《円》……」
僕「そして $a + b$ が一定の数になるような $a$ と $b$ の組み合わせをぜんぶ考える」
ユーリ「あっ、お兄ちゃん。もう何も言わないで。言っちゃダメ。ユーリ完全に理解した。描いてみる!」
僕「はいはい」
ユーリは紙をつかんでさっそく描き出した。
やってみよう
あなたも、 二点 $A$ と $B$ からの歩数ではかった距離の和が一定の値になる点の集合を描いてみましょう。
それは《格子点の世界》の《楕円》といえます。

※こちらにPDFを用意しました。ダウンロードして自由にご利用ください。

ユーリ「$A$ から $a$ 歩で、 $B$ から $b$ 歩で、 $a+b$ を一定にするんだよね。えーと……何歩にすればいい?」
僕「……」
ユーリ「ねー! 無視しないでよー!」
僕「何も言っちゃ駄目なんだろ?」
ユーリ「意地悪」
僕「とりあえず、 $a+b$ をあまり小さくしたらまずいよね。 $A$ と $B$ の距離 $AB$ がそもそも $4$ だから……」
ユーリ「そっか。 $AB=4$ だから、 $a+b$ は $4$ 以上じゃないとまずいか……だって、 $a+b = 4$ になる点は、 ちょうど真ん中にある一点しかないもんね?」
僕「え?」
ユーリ「え、違う? $A$ から $2$ 歩と、 $B$ から $2$ 歩……じゃない?」
$a+b=4$ になる点は一つしかない?
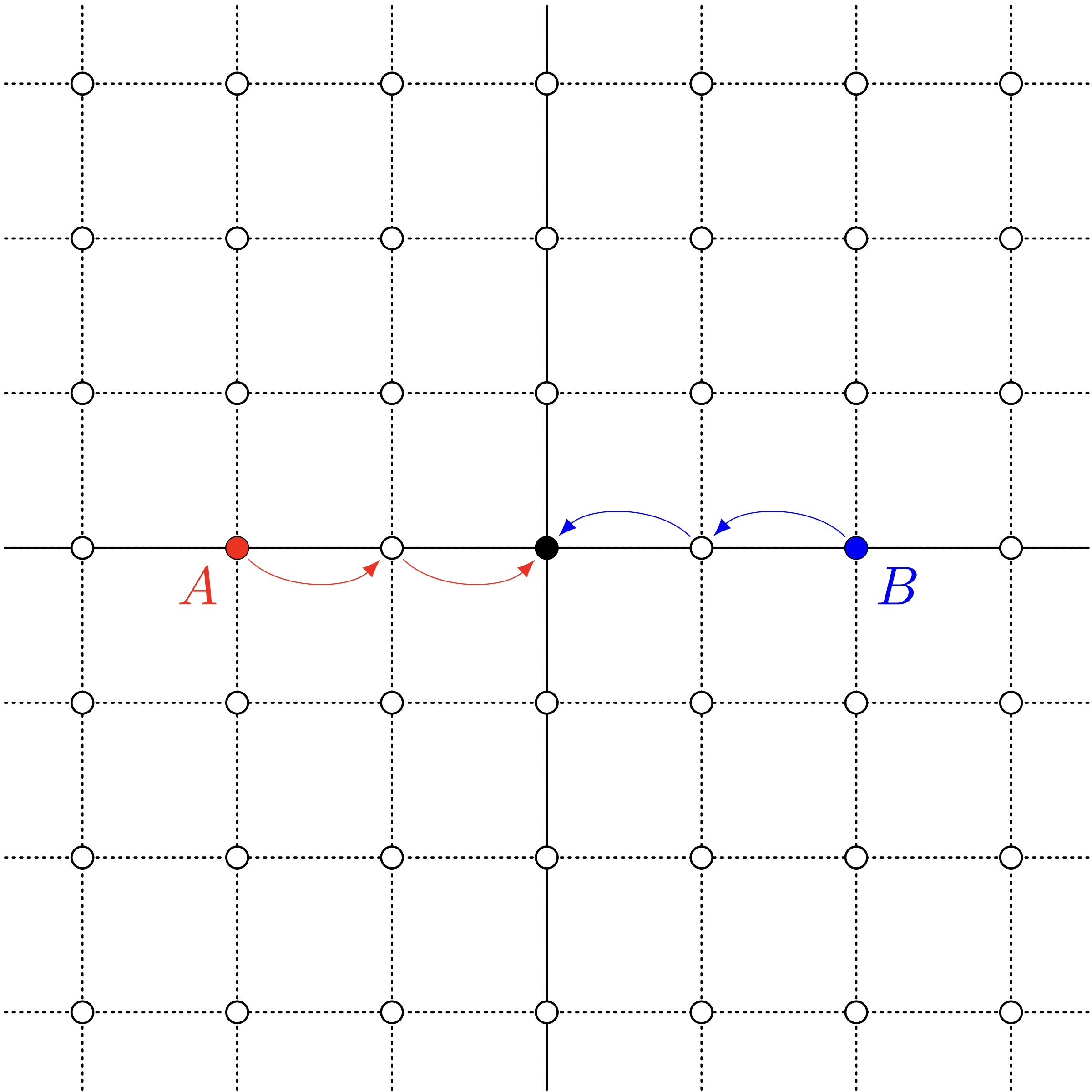
僕「$a=2,b=2$ の場合は確かに $a+b=4$ になるけど、 $a=1,b=3$ でも $a+b=4$ になるよ」
$a=1, b=3$ のとき、 $a+b=4$ になる
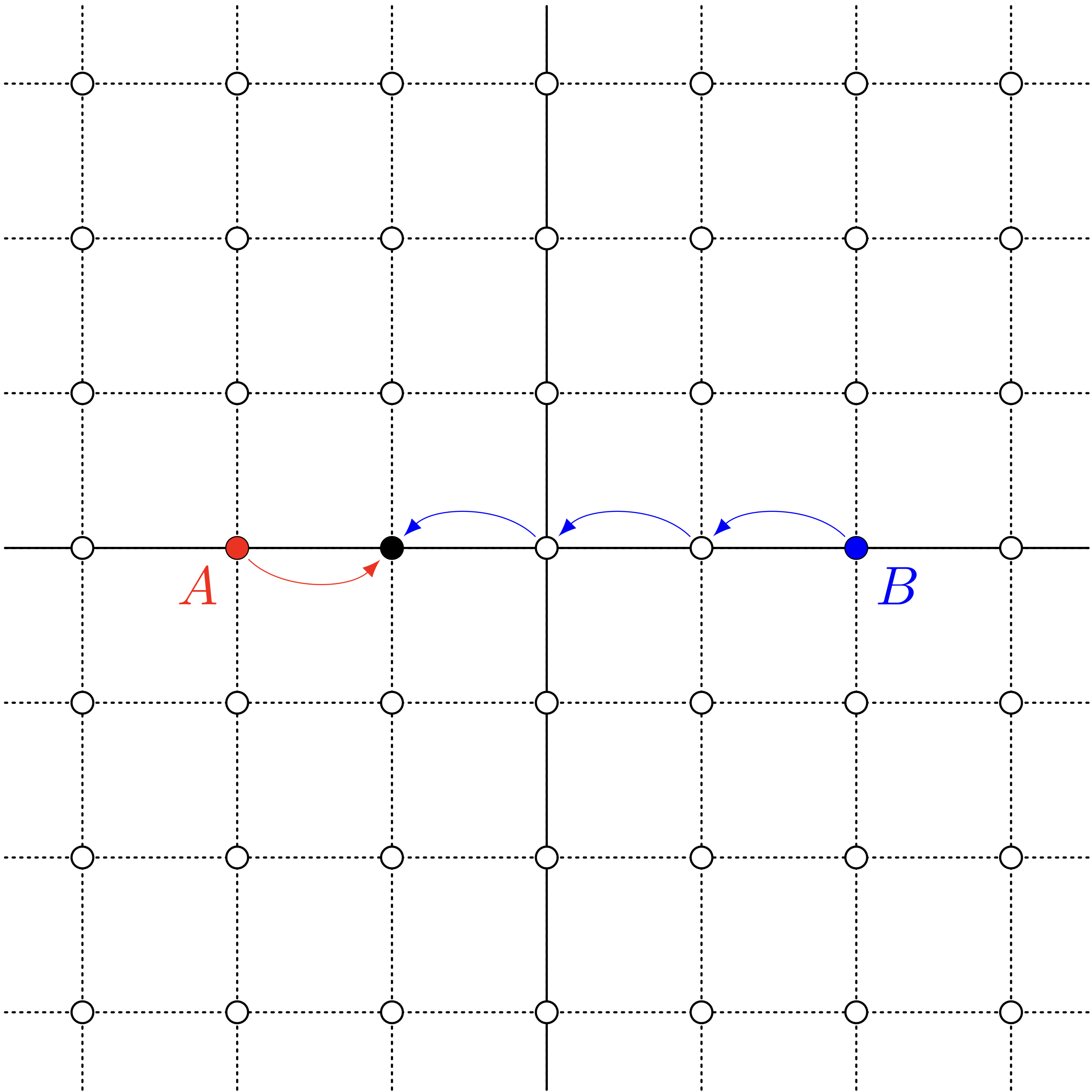
ユーリ「あっ、そーか。だったら——」
僕「それからさらに、 $a=0,b=4$ でも $a+b = 4$ になる」
ユーリ「いま、ユーリがそれ言おうと思ったのに!」
僕「はいはい」
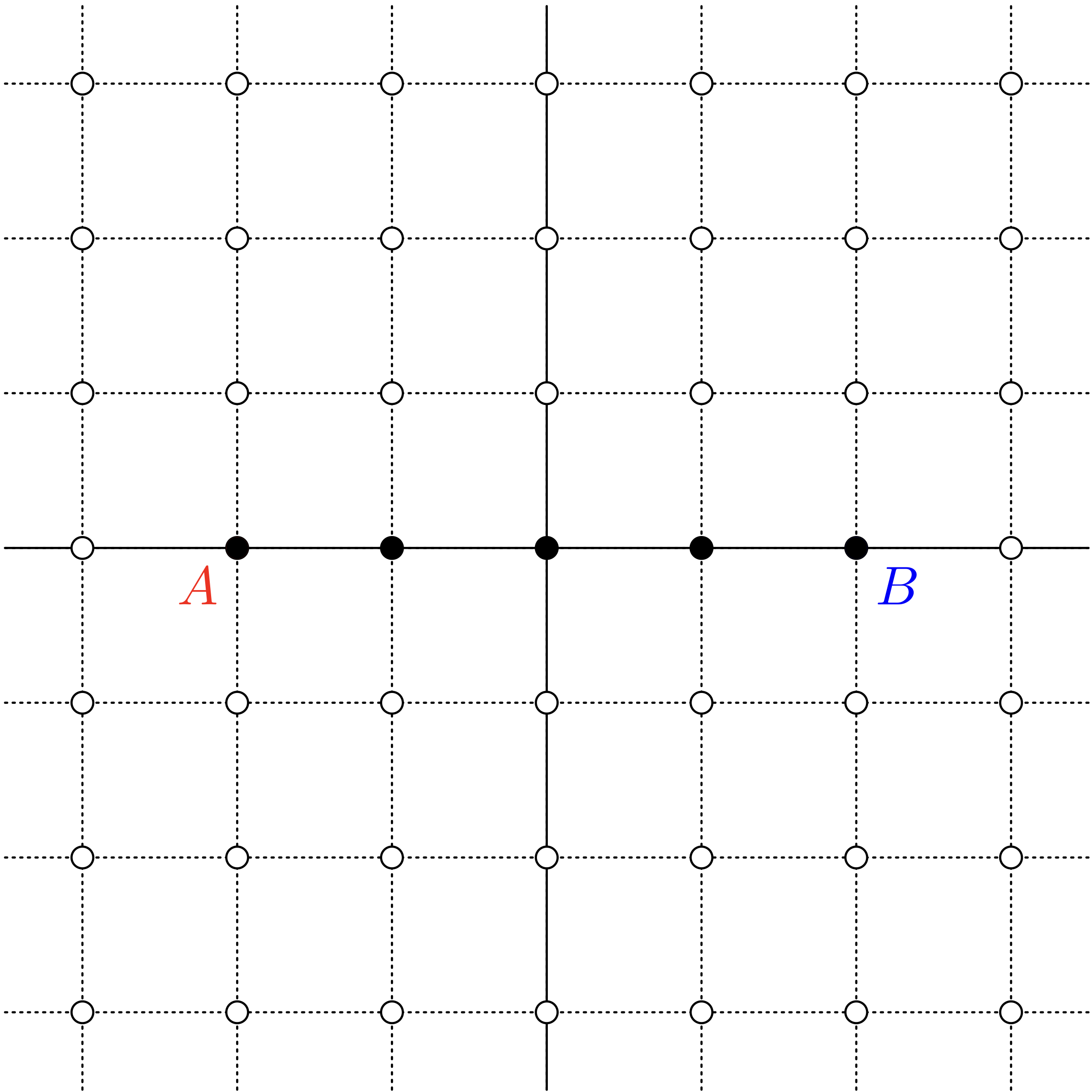
$a=0,b=4$ のとき、 $a+b=4$ になる
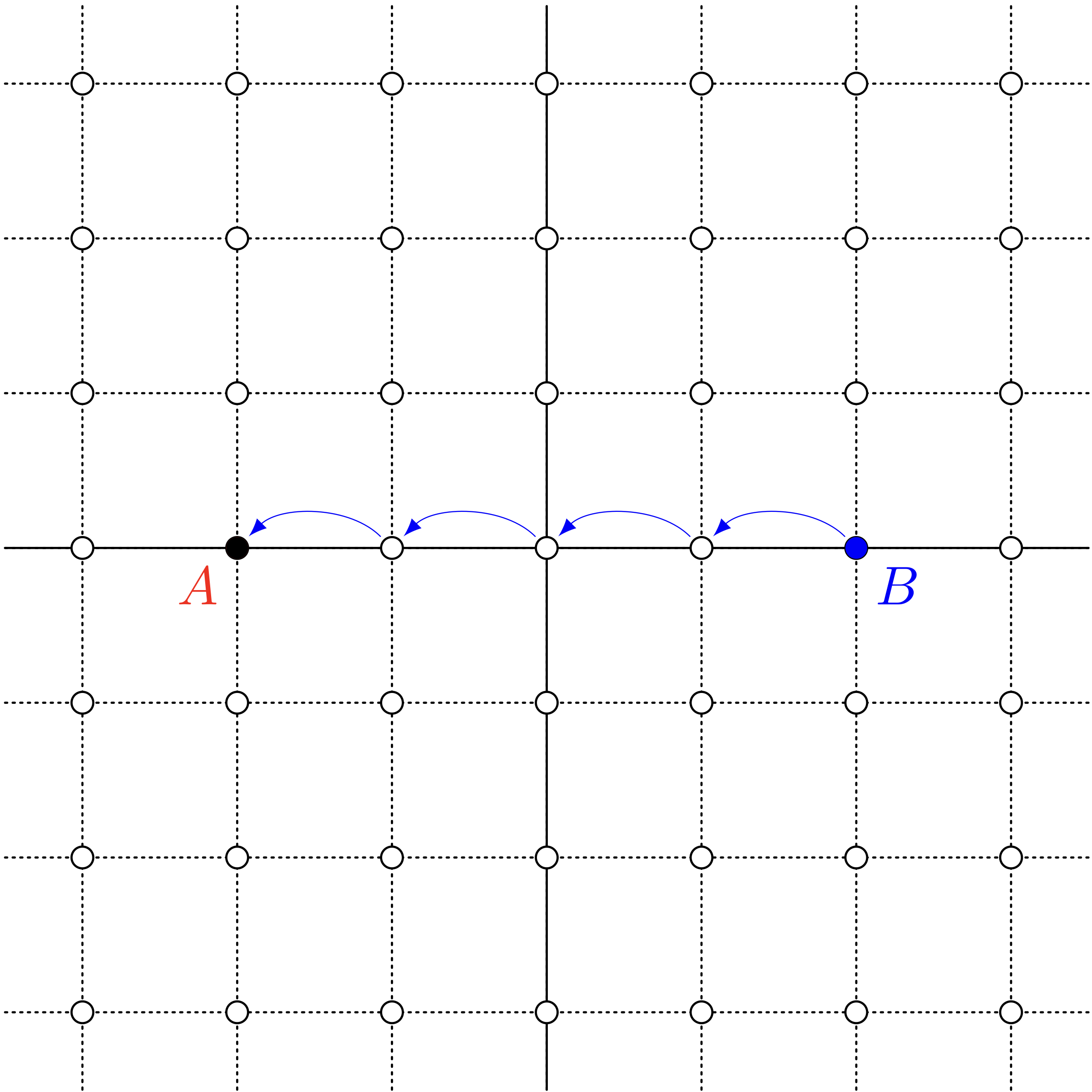
ユーリ「……ってことは、 $a + b = 4$ になる《楕円》は、 この $5$ 点ってことかにゃ?」
$a+b=4$ となる《楕円》がわかった
僕「そうなるね」
ユーリ「ぜんぜん楕円っぽくなーい!」
僕「それは二点間の距離 $AB$ と $a+b$ が等しいからだね。 普通の平面上に描く楕円でいうなら、二つのピンに渡す糸が全然たるんでいない状態と同じだ」
ユーリ「あー確かに!ぺしゃんこになったのかー。 もうちょい、ゆとりがいるんだね。じゃあ、 $a+b = 4$ じゃなくて、 $a+b=5$ でやってみるー。 何もヒント言っちゃ駄目だかんね」
僕「はいはい」
ユーリは、しばらく無言で描いていたけれど、 やがて、うーうー言い出した。
ユーリ「うー……おかしい」
僕「$a+b=5$ だと《楕円》はどうなった?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年1月19日)