![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
ここは僕の部屋。 さっきまで本を読んでいたユーリがこんなことを言い出した。
ユーリ「ねー、お兄ちゃん。楕円描ける?」
僕「こうだろ?」
僕はノートの端に楕円を描いてみせた。……少なくとも僕は楕円のつもりだった。
僕がフリーハンドで描いた楕円
ユーリ「いやいやいや、そーゆー適当なのじゃなくて、もっとちゃんとしたの」
僕「え? フリーハンドにしては結構うまく描けたと思うけどなあ」
ユーリ「そーじゃなくて! ユーリは楕円の描き方知ってるかって聞いているの!」
僕「ああ、そういうことか。知ってるよ。こうだろ?」
楕円の描き方
1. ピンを二本立てる。
2. 糸を輪にしてピンに掛ける。
3. 糸がたるまないようにしながら、シャープペンでぐるっと一回りする。
4. 楕円のできあがり。
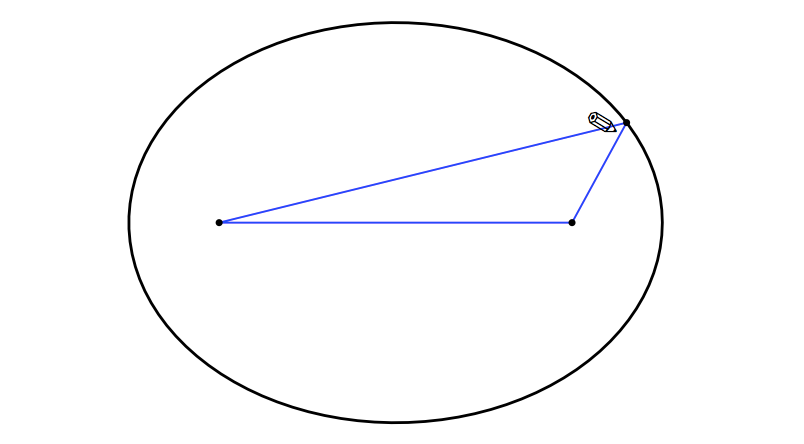
ユーリ「ちぇっ、知ってたか」
僕「高校生だからね。そのくらい知っているよ」
ユーリ「でも、ユーリが知ってるのと少しやり方違う。 糸を輪にするんじゃなくて、二本のピンのあいだに糸を張るんじゃなかったっけ」
僕「どっちでも同じだけど、糸を輪にしたほうが簡単だし、綺麗に描けるよ。糸を張ってしまうと、 糸がピンに絡むからぐるっと一回りできないし」
ユーリ「あ、そっか」
僕「二本のピンを離して描いたときと、近づけて描いたときでは楕円の形が変わるよね」
ユーリ「うん、そーだね」
二本のピンを離して描いた楕円
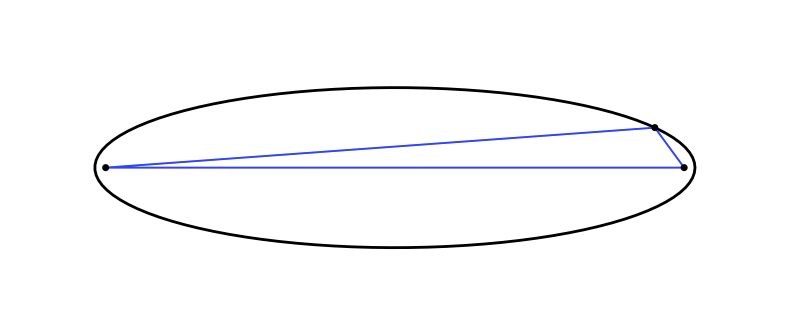
二本のピンを近づけて描いた楕円
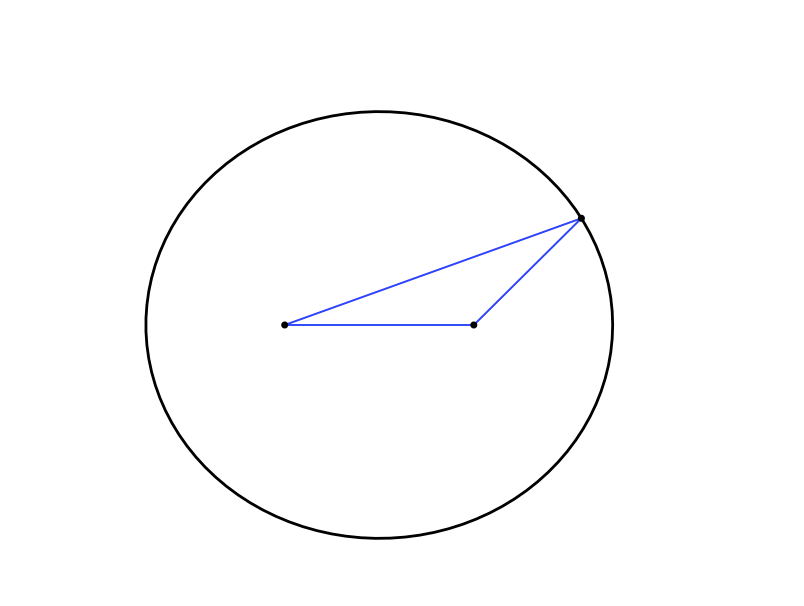
僕「二本のピンをずっと近づけて距離を $0$ にしたらどうなる? つまり、二本のピンが重なって一本になったとき」
ユーリ「簡単! 円になる!」
二本のピンを重ねて描いた楕円は円になる
僕「そうだね。だから《円は楕円の特別な場合》といってもいいわけだ」
ユーリ「それって《正方形は長方形の特別な場合》というのとおんなじ!」
僕「そうそう、そういうことだね」
僕「ところでユーリは《円の定義》って知ってる?」
ユーリ「そんなの知ってるよ。半径があって、円周がぐるっと丸い形でしょ?」
僕「……言いたいことはわかるけど、それを定義にするのはつらいなあ。 円というのがどういう図形か、いいかえると《どんな条件を満たす点の集合なのか》を言わなきゃ。 ほらほら、ユーリが好きな《バシッと》決めるのはいまだよ」
ユーリ「あ、思い出してきた。中心だ。《中心から半径だけ離れた点の集合》だね!」
僕「うん、さっきよりずっといい。少し言葉を補って定義の形にするとこうだよ。 円とは……」
円の定義
平面上で、ある一点からの距離が一定である点全体の集合を円という。
この《ある一点》のことを円の中心という。
この《一定の距離》を円の半径という。
ユーリ「ふーん。《平面上で》とわざわざ言ったのはなんで?」
僕「何でだと思う?」
ユーリ「そうしないと《球》になっちゃうから?」
僕「そうだね! 同じ定義で《平面上で》を《空間で》にしたら球になっちゃう。 ちゃんと円を定義するには《平面上で》と断る必要がある」
ユーリ「そだね」
僕「そして、この《円の定義》から《円の方程式》もすぐにわかるよ」
ユーリ「円のほーてーしき……」
僕「そうそう。《円の方程式》というのは、 円の上にある点を $(x,y)$ としたとき、 $x$ と $y$ はどういう条件を満たすかを数式で表したものだね」
ユーリ「出たな数式マニア」
僕「話を簡単にするために、中心が原点 $(0,0)$ にあって、 半径が $1$ になる円を考えてみよう。まずね」
ユーリ「ちょっと待ってよ、お兄ちゃん」
僕「がく。どうした?」
ユーリ「さっさかさっさか先に進まないでよ。 お兄ちゃんよく《ナントカを考えてみよう》って言うよね。 学校の先生もよく言うセリフ。すんごく先生っぽい」
僕「まあ、そうかもね」
ユーリ「何か問題が出てれば《考えてみよう》ってわかるけど、 《円を考えてみよう》って言われてもなー……って思うの」
僕「ほほう」
ユーリ「考えてみようと言われても、 何だかどこにもイキバのないヤルセナイ思いがアフレてくるみたいな」
僕「何だか意味不明なこと言い出したな」
ユーリ「へへ」
僕「でも、これはお兄ちゃんの言い方が悪かったよ。 ちゃんと問題を出してたつもりだったけど、はっきり言ってなかった。 《円を考えてみよう》というとき、実は問題は出てるんだよ」
ユーリ「どゆこと? どんな問題が出てるの?」
僕「《中心が原点 $(0,0)$ にあって、半径が $1$ になる円の方程式を求めよ》という問題。 もう少し言葉を補うと、こういう問題」
問題1(円の方程式)
中心が原点 $(0,0)$ にあって、半径が $1$ になる円の方程式を求めよ。
(すなわち、中心が原点 $(0,0)$ にあって、半径が $1$ になる円上にある点を $(x,y)$ としたとき、 $x$ と $y$ が満たしている関係式を求めよ。)
ユーリ「ふんふん。これなら確かに問題だね!」
僕「で。このような円を描いてみることになる。図形問題だから、図を描かなくちゃね。ポリアの《図をかけ》という問いかけ通り」
中心が原点 $(0,0)$ にあって、半径が $1$ になる円
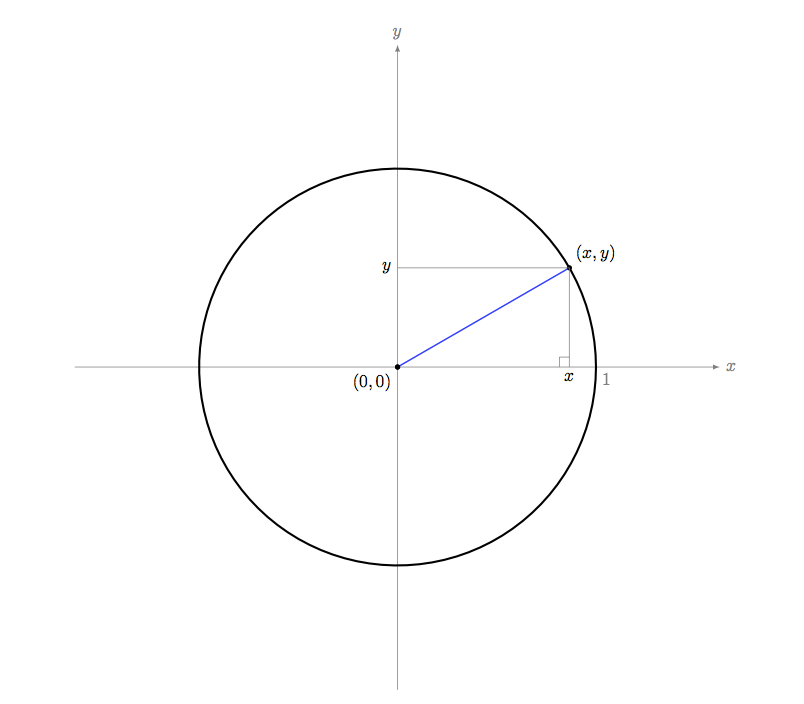
ユーリ「それで、円の方程式を求める?」
僕「そうそう。円上にある点を $(x,y)$ としたとき、 $x$ と $y$ にどんな関係がありますかということ。 これは直角三角形が見えているからすぐにわかるよね」
ユーリ「ピタゴラスの定理でしょ?」
僕「そう。ピタゴラスの定理(三平方の定理)から、こんな式が成り立つことがわかる。直角に向かい合っている辺、つまり斜辺の長さが $1$ に等しいから」
$$ x^2 + y^2 = 1^2 $$
解答1(円の方程式)
中心が原点 $(0,0)$ にあって、半径が $1$ になる円の方程式は、
$$ x^2 + y^2 = 1 $$
である。
ユーリ「え、これで終わり?」
僕「これで終わり。この円上にある点 $(x,y)$ は $x^2 + y^2 = 1$ を満たすし、 逆にこの式を満たしている点 $(x,y)$ はこの円上にあるから」
ユーリ「ふむふむ」
僕「ところでこの《円の方程式》を求めるときに、さっきの《円の定義》がちゃんと出てきているよね。 $x^2 + y^2 = 1$ というのは《点 $(x,y)$ は、原点 $(0,0)$ から一定の距離 $1$ にありますよ》ということを 表している式に読めるから。少し補うとすれば、こういう式で、 《原点 $(0,0)$ と点 $(x,y)$ の距離は $1$ に等しい》という関係が表現できる」
原点 $(0,0)$ と点 $(x,y)$ の距離は $1$ に等しい
$$ \SQRT{(x - 0)^2 + (y - 0)^2} = 1 $$
僕「一般に、二点 $(x,y)$ と $(a,b)$ のあいだの距離は、ピタゴラスの定理を使えばすぐに求まるよね」
二点 $(x,y)$ と $(a,b)$ の距離
$$ \SQRT{(x - a)^2 + (y - b)^2} $$
ユーリ「……」
僕「だから、一般的にいえば、点 $(a,b)$ を中心にして半径 $r$ になる《円の方程式》は $(x-a)^2 + (y-b)^2 = r^2$ ということになるね」
ユーリ「……ねー」
僕「何?」
ユーリ「その円の方程式って、 $\SQRT{(x-a)^2 + (y-b)^2} = r$ って書いちゃだめ?」
僕「え……そうか、うん。それでもいいね。どちらにしても半径 $r$ は負じゃないから、そう書いても正しい。 まあ教科書なんかにはその形では書いてないけど」
ユーリ「だってさー、 $\SQRT{(x-a)^2 + (y-b)^2} = r$ の方が《距離が一定》じゃん?」
僕「確かに。二点間の距離が一定で、半径 $r$ に等しいんだから、円の定義そのままだね」
僕「《円の方程式》がわかったら、《楕円の方程式》もすぐにわかるよ」
ユーリ「楕円にも方程式ってあるの?……そりゃあるか」
僕「そうだね。こんな楕円を考えよう。いいかい」
ユーリ「ほらまた!《ナントカを考えよう》が出た!」
僕「はいはい。それじゃ、問題問題」
問題2(楕円の方程式)
中心が原点 $(0,0)$ で半径が $1$ の円の、
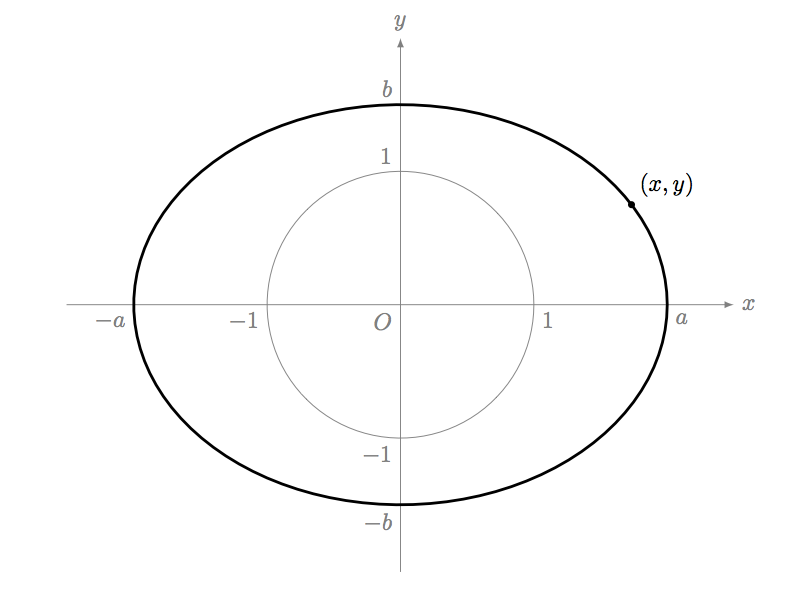
ユーリ「$x$ 座標を $a$ 倍し、 $y$ 座標を $b$ 倍した図形……?」
僕「つまり、横方向と縦方向に拡大縮小した図形ということだね。この図では両方拡大してるけど」
ユーリ「にゃるほど。円をぎゅうっと伸ばしたり縮めたりして楕円を作るんだね!」
僕「そうそう。これは簡単に求められるよ」
ユーリ「またピタゴラスの定理?」
僕「いや、そうじゃなくて、いまユーリが言ったように《円を伸ばしたり縮めたりする》んだ。 《円の方程式》はもうわかっているからすぐにできる」
ユーリ「方程式を伸ばすってどーすんの?」
僕「方程式を伸ばすというのとは違って……まあやってみようか。 まずはこの問題文の通りに式を立ててみるんだ。 これから図形……まあ楕円なんだけど……の上にある点を $(x', y')$ と置くことにする。 円の上にある点は $(x,y)$ で、楕円の上の点は $(x',y')$ ということだよ」
ユーリ「ふんふん?」
僕「それでと。《$x'$ は $x$ を $a$ 倍したもの》で《$y'$ は $y$ を $b$ 倍したもの》だよね。 だから、 $x$ と $x'$ の関係や $y$ と $y'$ の関係は式を使って書ける」
$$ \left\{\begin{array}{llll} x' &= ax \\ y' &= by \\ \end{array}\right. $$
ユーリ「ほほー。そのまんまだね」
僕「僕たちが求めたいのは、 $x'$ と $y'$ がどういう関係式を満たしているか、だ。 僕たちはその答えをまだ知らない。 $x'$ と $y'$ はどんな式を満たしているんだろう……でも、知っていることもある。 $x'$ と $y'$ の関係は知らないけど、 $x$ と $y$ の関係は知っているよね!」
ユーリ「$x$ と $y$ って何だっけ……円上の点だっけ」
僕「そうそう。だから、僕たちの問題2はこう言い換えられる」
$a,b,x,y,x',y'$ について、
$$ \left\{\begin{array}{llll} x^2 + y^2 &= 1 \\ x' &= ax \\ y' &= by \\ \end{array}\right. $$
が成り立つとき、 $x'$ と $y'$ の関係を表す式を求めよ。 ただし、 $a \geqq b > 0$ とする。
ユーリ「へー! 数式だけになった」
僕「さて」
ユーリ「これって、連立方程式を解くってこと?」
僕「うん。まあそういってもいいね。ここから消去するのは $x$ と $y$ だよ。 そうすれば $x'$ と $y'$ の関係式が出てくる」
ユーリ「えーと、 $x = \dfrac{x'}{a}$ と $y = \dfrac{y'}{b}$ を $x^2 + y^2 = 1$ に入れればいいの?」
僕「そうそう。ユーリ、いまさっと $a$ や $b$ で割ったけど、割ってもいいの?」
ユーリ「割っちゃいけないの? あ! 大丈夫。ゼロ割りにはならないよん。 だって、 $a$ も $b$ も $0$ より大きいから!」
僕「いいね!」
ユーリ「そんで……これでいい?」
$$ \begin{align*} x^2 + y^2 &= 1 \qquad \textbf{円の方程式} \\ \left(\dfrac{x'}{a}\right)^2 + \left(\dfrac{y'}{b}\right)^2 &= 1 \qquad \textbf{$x = \dfrac{x'}{a}, y = \dfrac{y'}{a}$を代入した} \\ \end{align*} $$
僕「うん、それでいいよ」
ユーリ「次は?」
僕「これでおしまい。だって、ほら、 $x'$ と $y'$ の関係式がもうできただろ? だから、楕円上の点を $(x',y')$ と置くと、 楕円の方程式は $\left(\dfrac{x'}{a}\right)^2 + \left(\dfrac{y'}{b}\right)^2 = 1$ となるんだね。 ふつうは図形の方程式は $(x,y)$ で表すから、 $\left(\dfrac{x}{a}\right)^2 + \left(\dfrac{y}{b}\right)^2 = 1$ が楕円の方程式」
解答2(楕円の方程式)
中心が原点 $(0,0)$ で半径が $1$ の円の、
$$ \left(\dfrac{x}{a}\right)^2 + \left(\dfrac{y}{b}\right)^2 = 1 $$

ユーリ「……」
僕「ほら、この《楕円の方程式》を見ても、円が楕円の特別な場合であることがわかるね。 この問題では $a \geqq b$ としたけど、ちょうど $a = b$ のときが円になる」
ユーリ「……」
僕「ユーリ、どうした?」
ユーリ「……お兄ちゃん、まちがってない?」
僕「いや、まちがってないと思うけど」
ユーリ「お兄ちゃんはこの問題2で《楕円の方程式》を求めるっていってたけど、 これは円を変形した図形の方程式だよね?」
僕「そうだよ」
ユーリ「でも、ほら、さっきお兄ちゃんがピンを二つ立てて描いた図形が楕円でしょ? 《二本ピンを立てて、糸を輪にしてぐるっと描いた図形》と 《円をタテヨコに変形した図形》って、どーして同じになるの? 同じっていえるの? ぜんぜん違う話じゃん!」
ユーリはそういうと、ふむっ!と鼻を鳴らして腕組みをした。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年7月18日)