![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「これ、なーんだ!」
ユーリは、出し抜けにそう言うと、僕の前に一枚の紙を置いた。

僕「何だと言われても……紙、だよね」
ユーリ「そーじゃなくって! この伏せた紙の表に何が描いてあるかを当てるの! アキネータークイズ、知らない?」
僕「ああ、はいはい。そういうことか。それは、生き物ですか?」
ユーリ「いーえ!」
中学生のユーリが僕にふっかけてきたのは、最近流行っている当て物クイズだ。
彼女は《何か》を紙に描いて伏せている。
僕は「それは○○ですか?」のような問いかけを繰り返し、 ユーリからの答えを聞いて《何か》が何であるかを当てるクイズ——というか、ゲームだな。
僕「それは、食べ物ですか?」
ユーリ「いーえ!」
僕「それは……コンビニで売ってますか?」
ユーリ「いーえ!」
僕「ユーリ、うれしそうだな」
ユーリ「お兄ちゃん、かすりもしてないからにゃ」
ユーリは、近所に住んでいる僕のいとこの中学生。
小さい頃からいっしょに遊んできたから、僕のことをお兄ちゃんと呼ぶ。
僕「それじゃ、もっと大きく行こうかな。それは物体ですか?」
ユーリ「いーえ!!」
僕「物体じゃない……ということは、それは概念ですか?」
ユーリ「えーと、たぶんそう」
僕「ああ、そうか。それは——数学に関係ありますか?」
ユーリ「はい。やっと来た」
僕「それは、フィボナッチ数列ですね!」
ユーリ「違いまーす。なんでやねん」
僕「ピンポイントで当てられると思ったんだよ……じゃ、数式ですか?」
ユーリ「違う」
僕「定理ですか」
ユーリ「違ーう」
僕「じゃあ……図形ですか?」
ユーリ「はい!!」
僕「それは、放物線ですね!」
ユーリ「違うって。なんで一発で当てようとするかなー」
僕「図形だよね……平面図形ですか?」
ユーリ「はい」
僕「対称性がありますか?」
ユーリ「はい」
僕「わかった。円ですか?」
ユーリ「はい、正解! やれやれだぜ」
わざとらしく肩をすくめてみせるユーリ。
僕「いや、意外に難しいんだよ、これ」
ユーリ「でもね、お兄ちゃんが驚くのはこれからだよん」
僕「驚くって、円を見て驚くってこと?」
ユーリ「そうでーす。さあ驚け! じゃじゃーん!」
ユーリはそういうと、大げさに紙を裏返す。
そこには——こんな図形(?)が描かれていた。

僕「え? これは円じゃないよね。点が並んでいるだけだ」
ユーリ「驚いた?」
僕「驚きはしないよ。ああ、この一個一個が円になってるってこと?」
ユーリ「違う違う。これ全体が一つの《円》なんだよん。ここからが本当の謎! さーさー、お兄ちゃん、わかるかにゃ?」
相変わらずユーリは、猫語でぐいぐい煽ってくるなあ。
僕「うーん、これは菱形に並んだ点だよね。菱形というか、正方形というか。 この形は、常識で考えると円とは言わない……」
ユーリ「そこで非常識で考えると……」
問題
ユーリは、この図形が《円》だという。それはどういう意味だろうか。


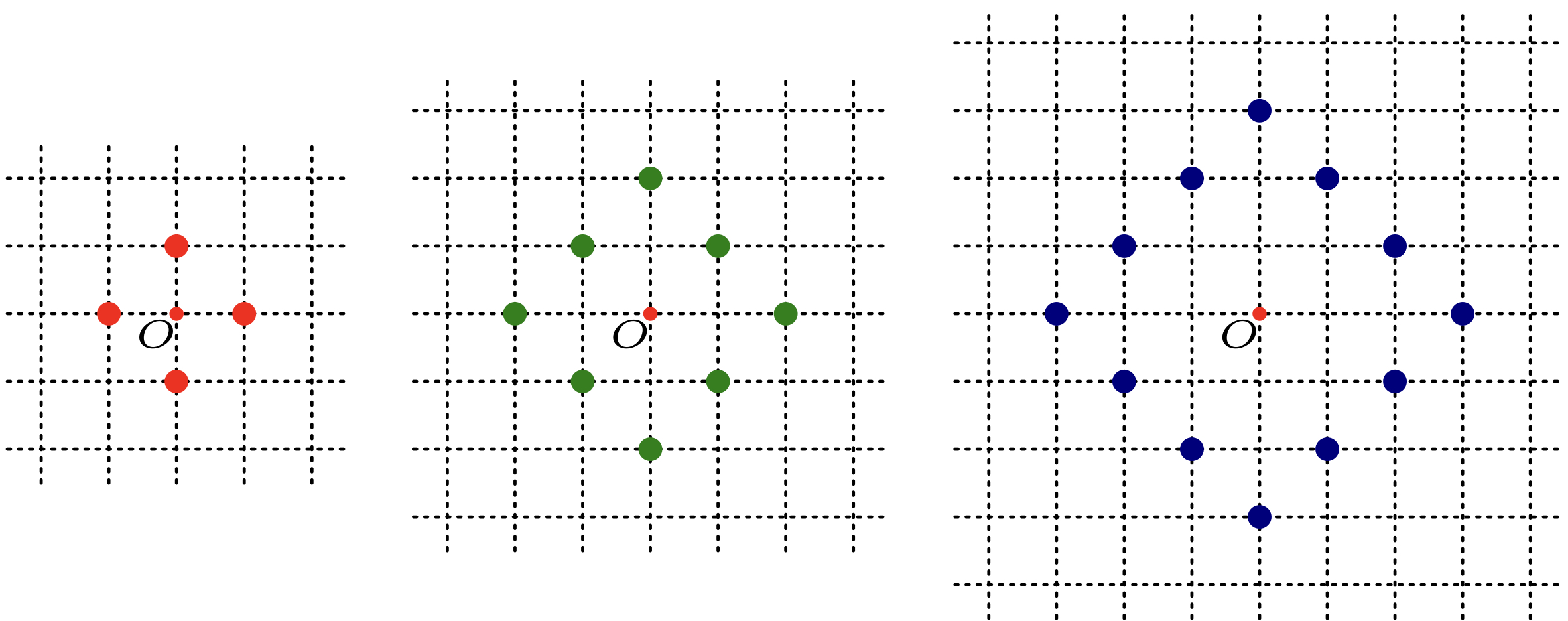
僕「この点は $12$ 個ある。この個数は重要かな……いや、重要じゃないな、きっと。 個数じゃなくて、点が並んでる形に意味があるんだよね?」
ユーリ「さっすがお兄ちゃん、いーとこ突いてきますなあ……その通り、形が重要だよん。 たとえば、こーゆーのも全部《円》になるのさ!」
これらもそれぞれ《円》になる
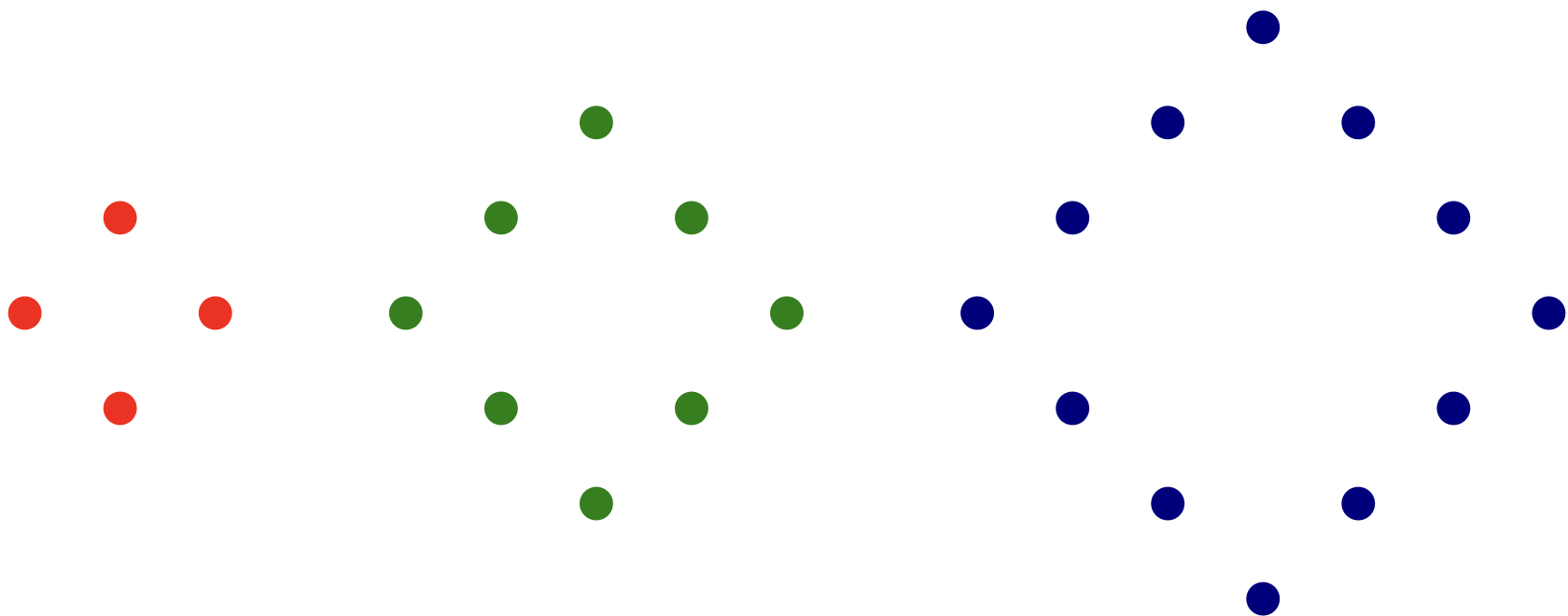
僕「なんでこれが円なんだ……」
ユーリ「やっぱ、そー言いたくなるよねー。ユーリもそーだったよ」
僕「ははーん。出題元は例のボーイフレンドか!」
ユーリには「数学対決」しているボーイフレンドがいるのだ。
……「数学対決」って何だよ。
ユーリ「ボッ、ボーイフレンドとか、そーゆーんじゃないからね、言っとくけど。 で、どーしてこれが《円》になるかわかった? 答え言ってもいい?」
僕「だめ。ちゃんと考えさせてほしい。絶対わかるから」
ユーリ「ちぇっ」
僕は深い思考モードに入る。
そうか。 これはパズルや謎解きじゃなくて、数学として考えるべきなんだ。
僕「……」
ユーリ「おーい」
僕「わかった!」
ユーリ「早!」
僕「わかったよ。 マス目が描かれてないのは、ミスリーディングだなあ」
ユーリ「みすりーでぃんぐって何?」
僕「誤解を招きやすくしているってこと。 こんなふうに線を描くのを思いついたら、意味がわかった」
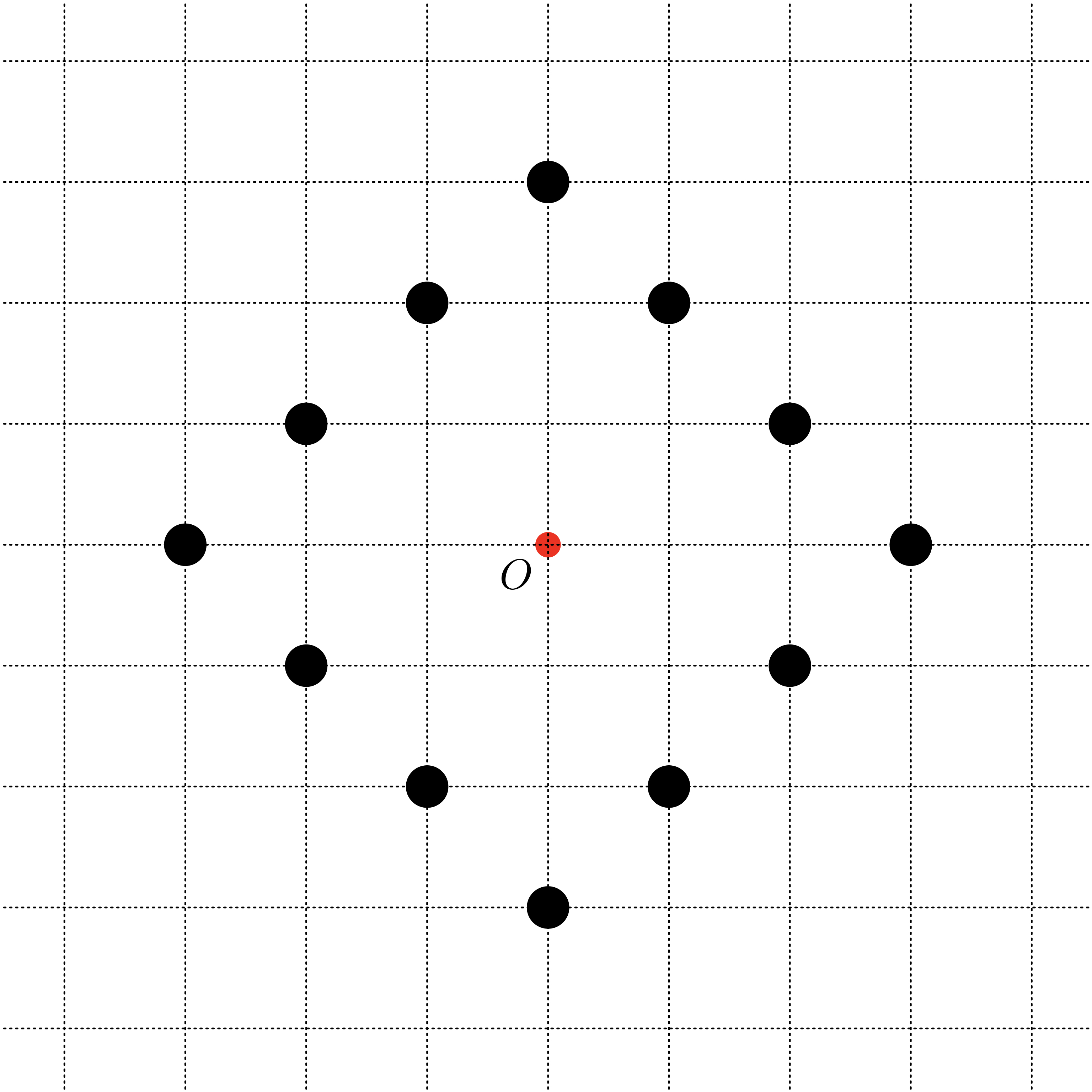
ユーリ「おー、さすがお兄ちゃん」
僕「線に沿って、 $1$ 目盛り進むことを『$1$ 歩』と考えることにする。 この線を格子状になった道だと考えるんだね。 歩く向きを変えることができるのは、道が交わった十字路のところだけ。 菱形に並んだこの点はどれも、点 $O$ から『$3$ 歩』のところにあるといえる。 だから、この菱形の図形はいわば半径が $3$ 歩の《円》と呼べるって言いたいんだね」
半径が $3$ 歩の《円》

ユーリ「そだねー」
僕「面白いなあ。もちろんいわゆる丸い円じゃないけど、 これは、格子点の世界で考えた《円》というわけだ」
ユーリ「こーしてん?」
僕「格子点は、座標平面で $x$ 座標と $y$ 座標がどちらも整数になる点のこと。 点を $(x,y)$ で表したとき、 $(0,0)$ や $(3,2)$ は格子点だけど、 $(0,0.5)$ や $(3.1,2.3)$ は格子点じゃない」
格子点
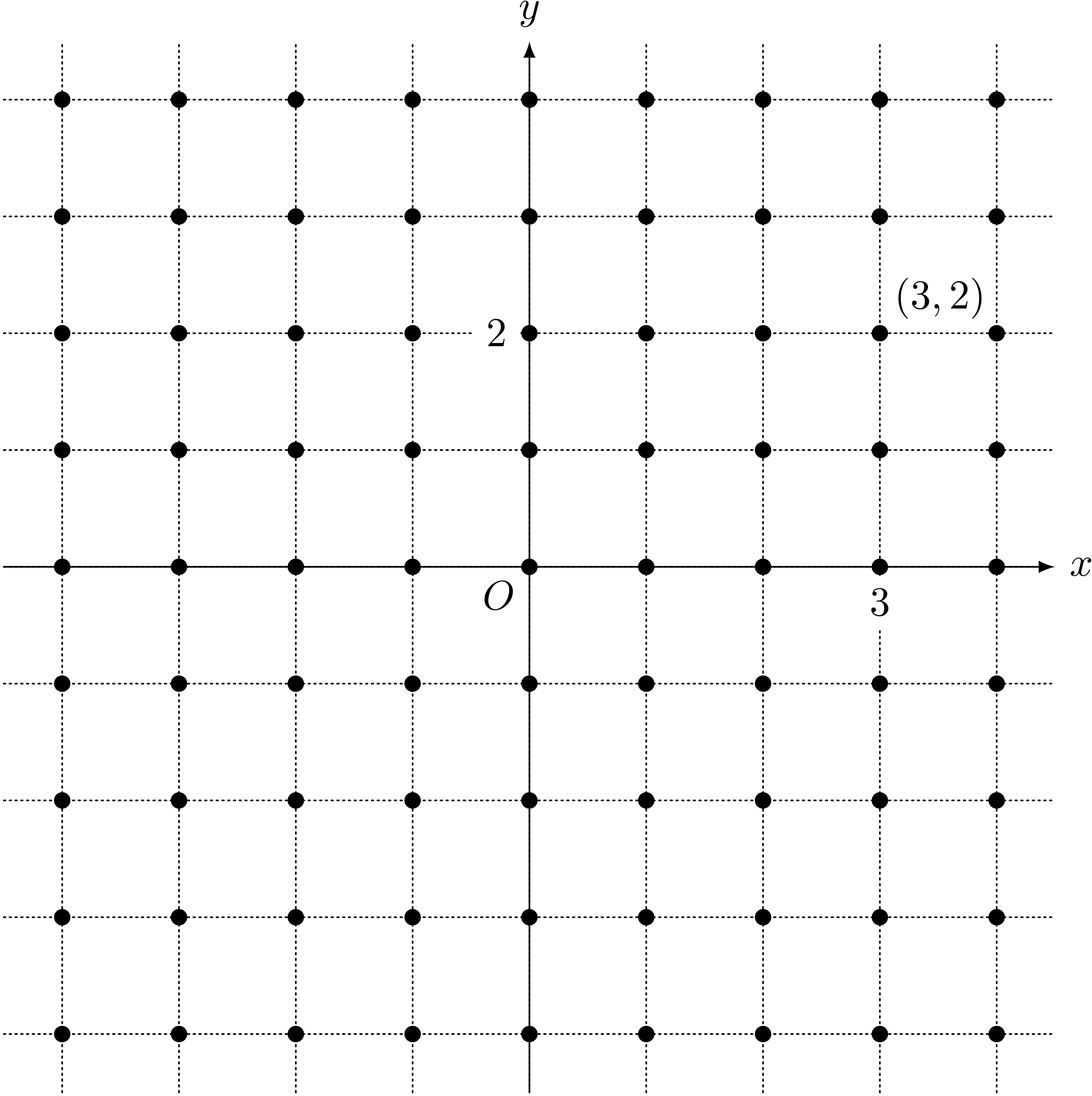
ユーリ「格子点……」
僕「円とは何か。その円の定義を別世界に持っていったんだよね。 通常の平面の世界の円から、格子点の世界の《円》に……」
ユーリ「そっか、そー考えるのか……」
僕「何だ、彼氏は説明してくれなかったの?」
ユーリ「説明してたけど、よくわかんなかった。あっと、彼氏じゃないけどね」
僕「『円とは何か』というのは、 別の言い方をすると『円の定義を述べよ』ということになるよね」
ユーリ「ふんふん。それはわかる」
僕「円の定義は、なーんだ」
ユーリ「わかる。一点から等距離にある点ぜんぶの集合だよね?」
僕「惜しい」
ユーリ「ん? あーそだそだ。平面上でが抜けてた」
僕「そうだね。円というのは『平面上で、一点から等距離にある点全体の集合』。それが通常の円の定義だね」
ユーリ「あれでしょ? 『平面上で』が抜けると、『球』になっちゃうかもしれないってことでしょ?」
僕「そういうこと。『平面上で』を『三次元空間で』に変えて、 『三次元空間で、一点から等距離にある、点全体の集合』となると、 それは通常は、円という平面図形じゃなくて、球と呼ぶ空間図形になる。空間図形というか立体というか。 ユーリはよくわかってるなあ」
ユーリ「ふふん」
円と球
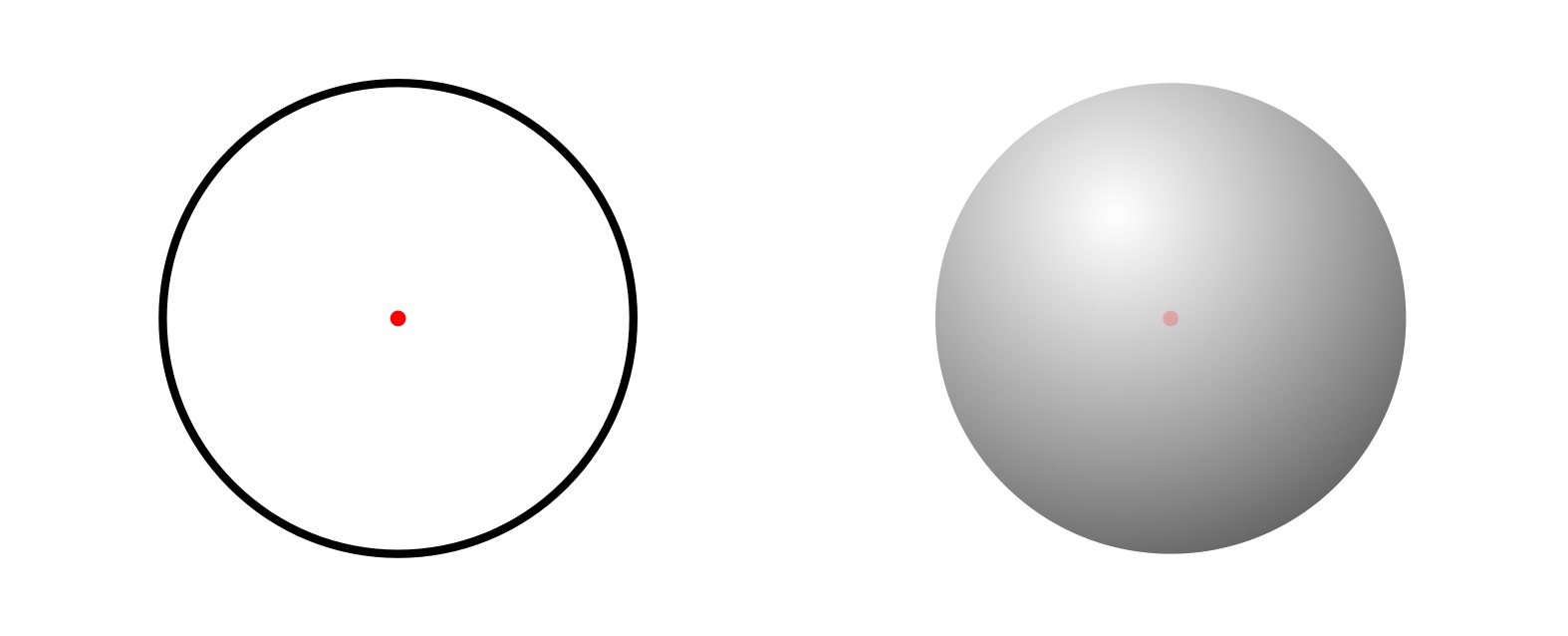
僕「でも、円と球は定義を見比べるとそっくりだといえる」
ユーリ「そーゆーふーに並べるんだったら、『平面上で』は『二次元空間で』の方がいい?」
僕「おお。まさにそう。そういうこと!」
ユーリ「へへん」
僕「こんなふうに並べると、『円』と『球』の違いというのは、 どういう空間で考えているかの違いといえる。 別の言い方をすると、 いわゆる円は『二次元空間における《球》』だし、 いわゆる球は『三次元空間における《円》』といえる」
ユーリ「おーおー、なるほど!」
僕「どの空間で考えるかを切り換えることで、 球と円を同一視できるといってもいい」
ユーリ「どーいつし?」
僕「一見すると違うように見えるものを、同じものだと見なすこと」
ユーリ「ああ、同一視ね」
僕「ユーリのクイズも、これと同じ話だよ」
ユーリ「へ? 何が同じなの?」
僕「ユーリが描いたその菱形に並んだ図形は、《格子点の世界》における《円》といえる」
ユーリ「たーしーかーに! 確かに! めっちゃわかった。 えっと、ユーリもわかってたんだよ。でも、お兄ちゃんにそー言われると、すごく納得」
僕「《平面の世界》の円と、《格子点の世界》の《円》をつないだことになる。 こういう《二つの世界》をつなぐ話はすごく楽しいよね!」
ユーリ「わかるー」
僕「考えてみると、さっき『半径が $3$ 歩の《円》』と言ったときの『半径』という言葉も、 《平面の世界》から《格子点の世界》にするっと移っていった言葉だよね」
ユーリ「えっと——」
そこで急にユーリは無言になる。
軽口を叩いていても、思考モードに入るとスッと口を閉じる。
話しながら考えるときもあるけれど、 自分の中で納得ポイントを探っているときには自然と無言になる。
それは僕もユーリも変わらない。
たぶん、心の中での探索作業が忙しくて、発言まで手が回らないのだろうな。
僕「……」
ユーリ「——そだね」
僕「ユーリはいまの時間で、どういう納得ポイントにたどり着いたの?」
ユーリ「確かに、半径は $3$ 歩だなって」
僕「それだけ?」
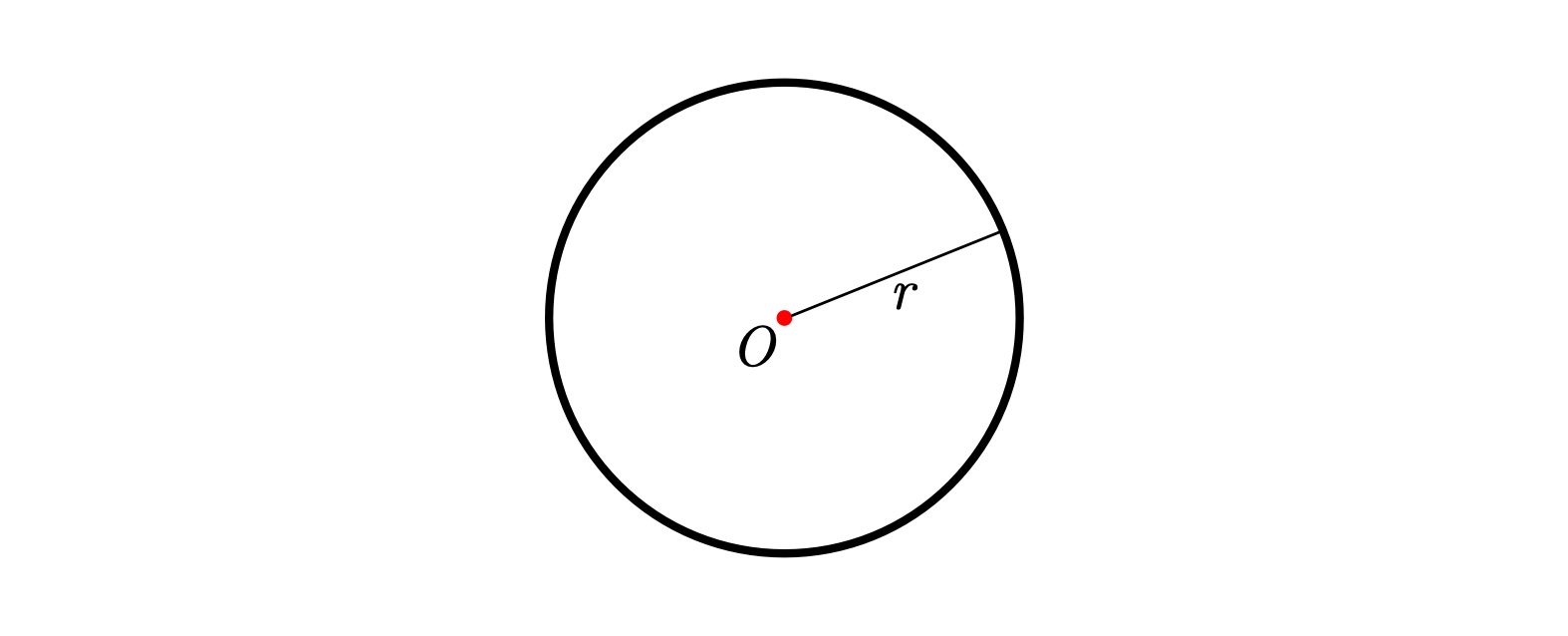
ユーリ「えーとねー『半径の定義』を考えてたの。 円の半径は、中心からの距離のことでしょ?」
僕「そうだね」
円の中心と半径
ユーリ「うん。だから、 さっき見せた三つの《円》は《格子点の世界》で半径が $1,2,3$ の《円》だよねー」
半径が $1,2,3$ の《円》
と、そこで何かが僕の心を打った。
僕「……」
ユーリ「お兄ちゃん?」
僕「……ねえ、ユーリ? 僕たちは《平面の世界》と《格子点の世界》とを行き来しているよね」
ユーリ「だね」
僕「いまさらだけど、二つの世界を行き来するための《パスポート》に気付いたよ」
ユーリ「何それ」
僕「《パスポート》でも《チケット》でもいいけど、つまり、《二つの世界》を行き来するために大切なもの。 これ、なーんだ?」
ユーリ「それは……図形ですか?」
僕「いいえ」
ユーリ「それは、数式ですか?」
僕「たぶんそう、部分的にそう」
ユーリ「それは、概念ですか?」
僕「はい」
ユーリ「それは、コンビニで売ってますか?」
僕「いいえ。おいおい、答え言ってもいい?」
ユーリ「よかろう」
僕「距離なんだよ」
ユーリ「きょり?」
僕「僕たちは《平面の世界》で考えている距離という概念を、《格子点の世界》に移した。 それによって、《平面の世界》にある円が自然と《格子点の世界》の《円》に移ったんだ」
ユーリ「……」
僕「何を言ってるかわかる?」
ユーリ「うーん……わかるような、わからないような」
僕「円の定義を思い出せばわかるよ」
ユーリ「平面上で、一点から等距離にある点全体の集合。 ああ、等距離ってところ?」
僕「そう、そうなんだ。 《格子点の世界》で距離が定義できたから、 《半径》という概念を持ってくることができて、 それで《円》という概念を持ち込むことができたといえる」
ユーリ「うん、それはわかる」
僕「ということは、距離を使って定義されている図形ならば、 円以外の図形も《格子点の世界》に持ってくることができることになる!」
ユーリ「距離を使って定義されてる図形……って、円以外にある?」
僕「もちろんあるよ。たとえば——」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第411回終わり)
(2024年1月12日)