![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕たちは、ユーリが持ち込んできた《格子点の世界》における《円》を議論していた(第411回参照)。
《異なる二点からの距離の和が一定》になる図形として楕円を思い付き、 試行錯誤しながら、僕たちはなんとか《格子点の世界》における《楕円》を描くことができた(第412回参照)。
ユーリ「……そんでもって、 結局 $a+b=6$ になる《楕円》はこうなった! 完成! たとえばこの点 $Q$ は $A$ から $2$ 歩、 $B$ から $4$ 歩のところにある!」
$a+b=6$ の《楕円》
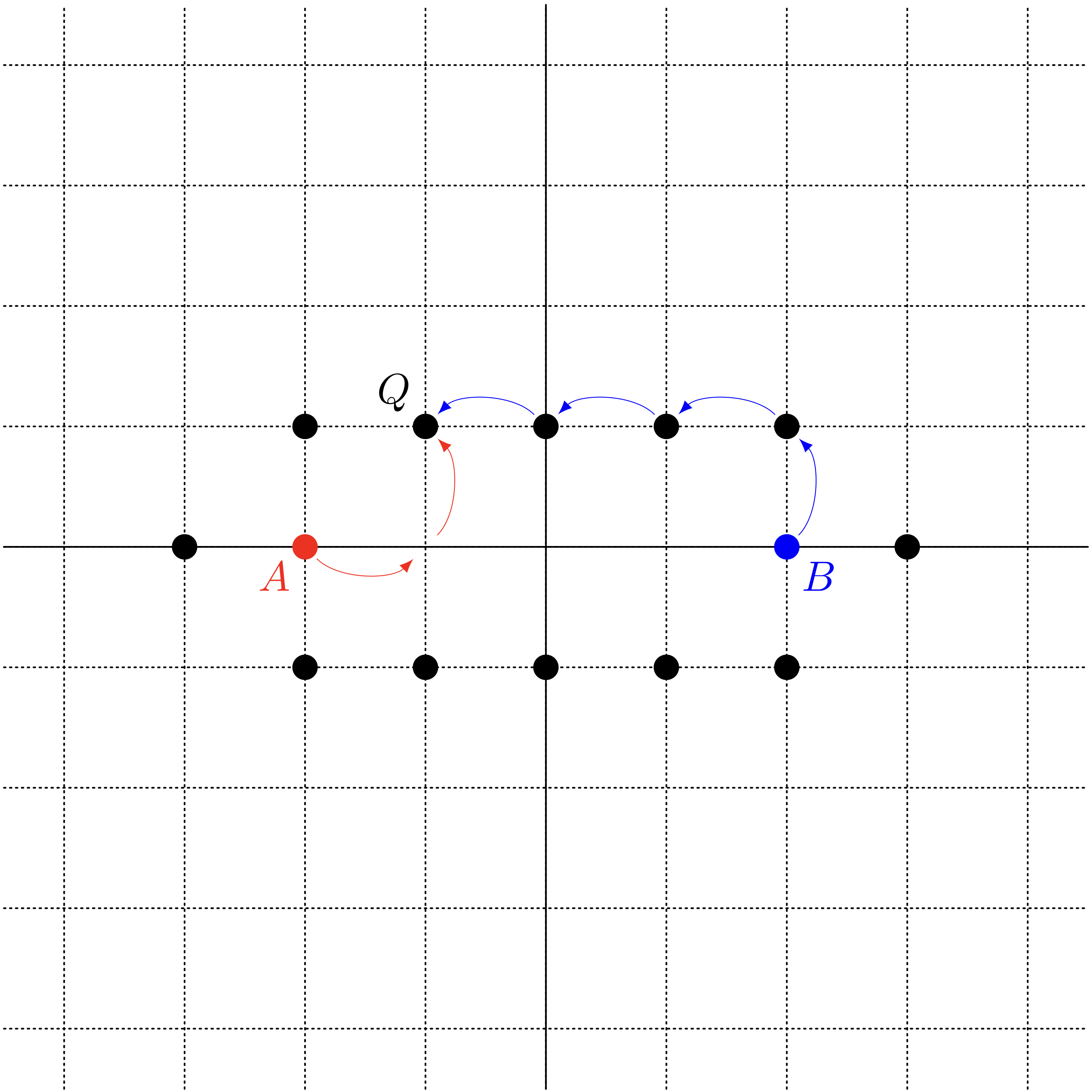
僕「……この《格子点の世界》の《楕円》は、《平面の世界》における楕円の面影があるなあ」
楕円の面影を感じる
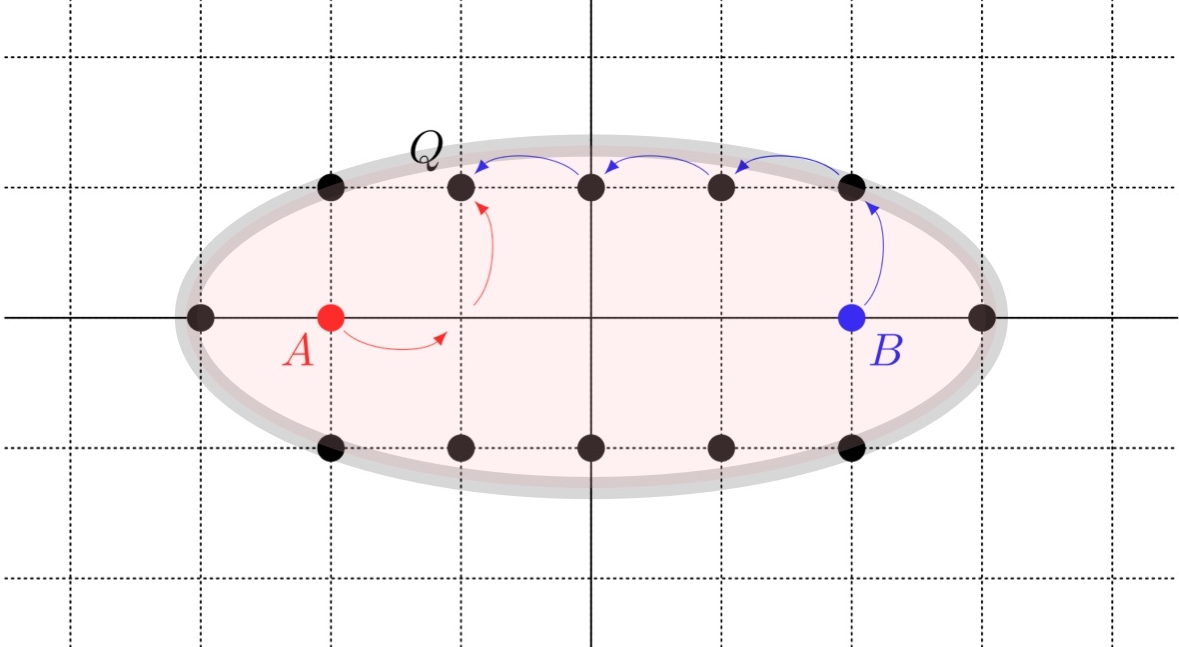
ユーリ「んー、でもこの大きさだと、小さくってちょっと物足りない感じ。 たとえば $a+b=8$ なら、もっと大きな《楕円》になるよね?」
僕「もちろん、そうなるね。そして $a+b$ を大きくすればするほど《楕円》は《円》に近づくんじゃないかな?」
ユーリ「$a+b=8$ の《楕円》を描いてみる! 《半径》が $a$ の《円》と、 《半径》が $b$ の《円》を描けばいいから、すぐできる!」
やってみよう
あなたも、 二点 $A$ と $B$ からの歩数ではかった距離の和が一定の値($8$)になる点の集合を描いてみましょう。
それは《格子点の世界》の《楕円》といえます。

※こちらにPDFを用意しました。ダウンロードして自由にご利用ください。

僕「どう?」
ユーリ「$a = 1$ と $b = 7$ だと交点ができなかったけど、 $a = 2$ と $b = 6$ なら、こんな感じになったよ」
《格子点の世界》における二つの《円》($a = 2$ と $b = 6$)

僕「なるほど。《格子点の世界》なら、 $a=2,b=6$ の二つの《円》は $5$ 個の点を共有するんだね。 《平面の世界》だと、二つの円が $5$ 個の点を共有するなんてことはありえない。 $0$ 個か、 $1$ 個か、 $2$ 個かしかありえない」
《平面の世界》での二つの円
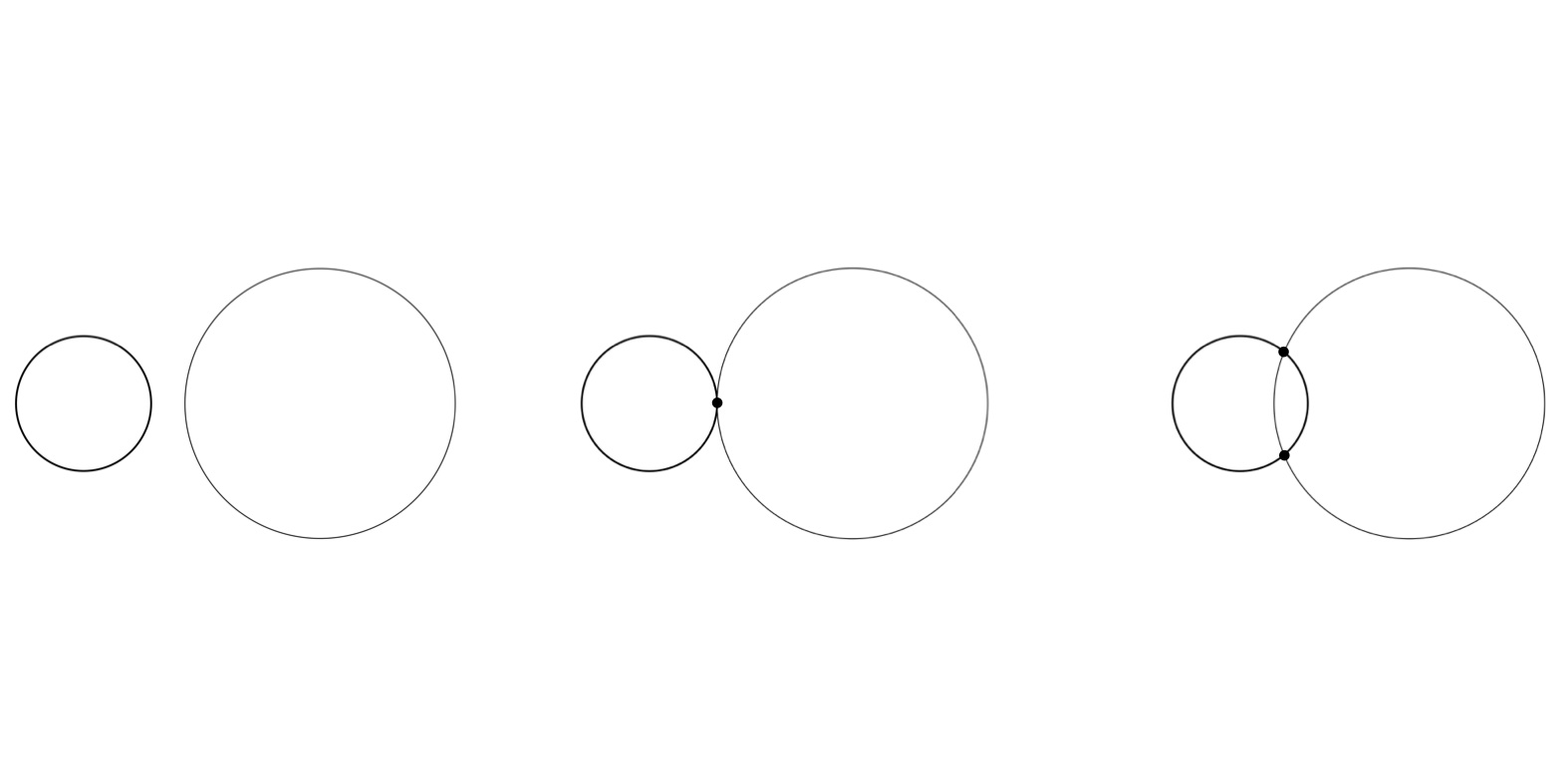
ユーリ「んーにゃ、違うね! 《平面の世界》だったら無限個の点を共有すること、あるじゃん」
僕「ん? ああ、確かに。中心が同じで半径が等しい二つの円が一致するときだね。 確かにそれは無数の点を共有してるといえる。鋭いな、ユーリ」
ユーリ「ふふーん……それにしてもさー、これ面白いよね。 二つの《円》は $5$ 個の点を共有していて——これって、面白いね!」
くすくす笑い出すユーリ。
二つの《円》が共有している $5$ 個の点

僕「何が? 何がそんなに面白い?」
ユーリ「あの、あのね。 この $5$ 個の点って——《半円》だよね!」
《平面の世界》の円と半円
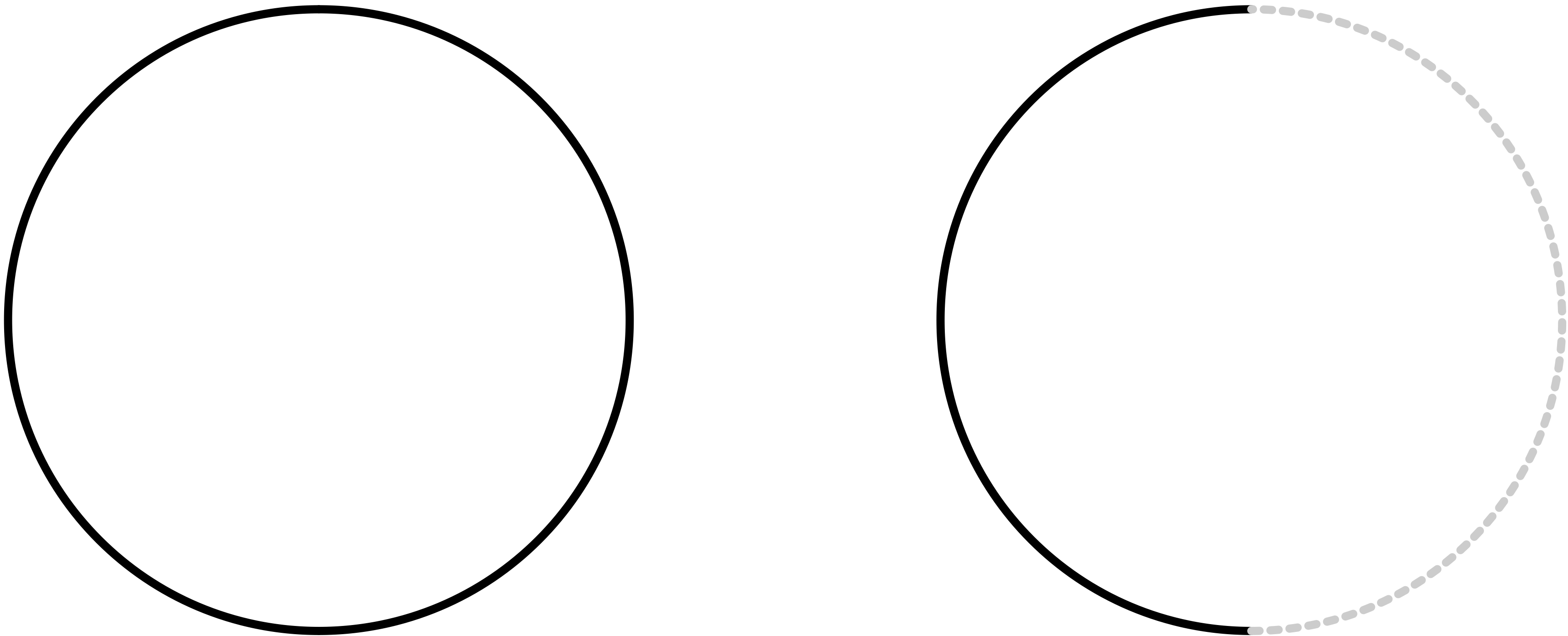
《格子点の世界》の《円》と《半円》
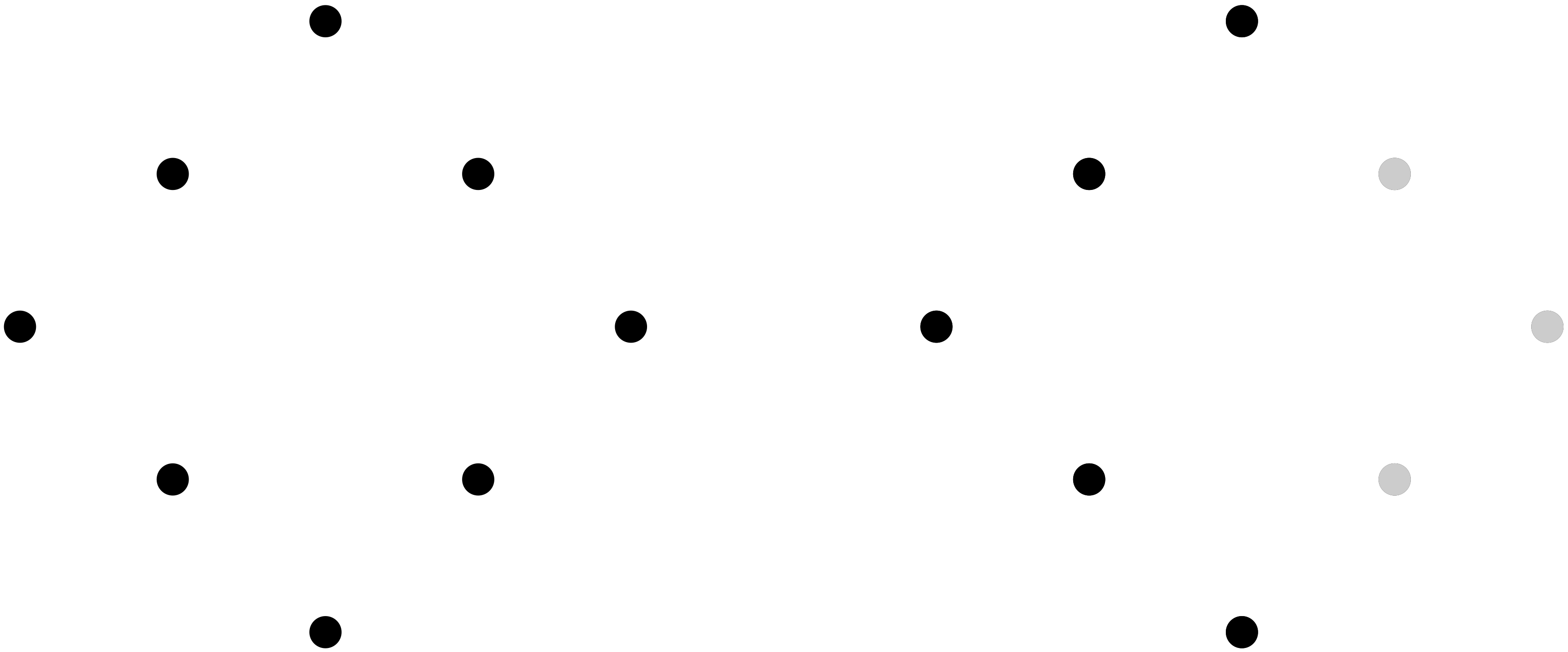
僕「あはは! まったくだ。《半円》だね! ということは、 $a=2,b=6$ は半円で接してるんだ!」
ユーリ「だよね! ものすごい接し方! 《半円》で接するんだって、あはは!」
僕とユーリは、しばらく笑いがとまらなかった。
後から落ち着いて考えると、 何がおもしろいのか自分たちでもわからなかったけど、 不思議な笑いのツボにはまったのだ。
僕「……ああ、笑った。いったい何がおかしいんだろう」
ユーリ「お兄ちゃんがゲラゲラ笑うから、つられてユーリも笑ったじゃん!」
僕「いやいや。いまは $a+b=8$ の《楕円》を描こうとしてたんだよね。ぜんぜん進まないなあ」
ユーリ「ちゃちゃっと描く! $a = 3$ で $b = 5$ だと、 二つの《円》は二点で交わるよ。こーなった」
二つの《円》($a = 3$ と $b = 5$)

※ $a=2,b=6$ で見つかった $5$ 点はグレーにしています。
僕「$a = 4$ と $b = 4$ は僕も描きたいな」
ユーリ「描かせてあげよう!」
二つの《円》($a = 4$ と $b = 4$)

※ $a=2,b=6$ で見つかった $5$ 点と、 $a=3,b=5$ で見つかった $2$ 点はグレーにしています。
僕「あとは左右の対称性から、 $a+b=8$ の《楕円》全体を描くことができるな。 たとえばこの点 $Q$ は点 $A$ から $3$ 歩、点 $B$ から $5$ 歩になっていて、 $3+5=8$ だ。 他の点もぜんぶ $a+b=8$ になっている。 確かにこれも楕円の面影がある。……ユーリ?」
$a+b=8$ の《楕円》

ユーリ「……」
僕「ユーリは何を考えてるんだろう」
ユーリ「……あのね。ユーリ、見えちゃったよ」
僕「何が?」
ユーリ「《格子点の世界》の《垂直二等分線》!」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年1月26日)