![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ある日の放課後、僕がいつものように図書室に行くと、 テトラちゃんがノートに向かい、うなっていた。
僕「今日は《ライオンテトラ》なの?」
テトラ「あ、先輩! 《ライオンテトラ》とは何でしょうか?」
僕「いや、ガルルル……ってうなってたからね。 テトラちゃんが《ライオン》になったのかなって思ったんだ」
テトラ「《ライオンテトラ》よりも《テトライオン》がいいですね——って、テトラはライオンじゃありませんし、 ガルルルなんてうなってませんようっ! ……うなってました?」
僕「ちょっとね」
テトラ「あたしは、 村木先生からの《カード》で式の計算をしてたんです」
僕「ああ、カージオイドの続き?(第367回参照)」
テトラ「あ、いえ、そうじゃありません。村木先生から、こんな問題を新たにいただいたんです」
テトラちゃんがもらった《カード》
平面上に二点 $F_1(-a, 0),F_2(a, 0)$ があります。 $a$ は正の実数です。
《線分 $PF_1$ と線分 $PF_2$ の長さの積は $a^2$ に等しい》という条件を満たす点 $P$ が作る曲線を $L$ とします。
曲線 $L$ について自由に考察してください。
僕「なるほど。曲線 $L$ は楕円かな?」
テトラ「えっ!」
僕「おっと、違うね。一定なのは《和》じゃなくて《積》か。ごめんごめん。楕円じゃなかった」
テトラ「ああ、びっくりです。一瞬で答えがわかる問題なのかと思っちゃいました」
僕「もしも $PF_1$ と $PF_2$ の《和》が一定の点 $P$ を考えるなら、 点 $P$ が作る曲線は楕円になる。 だから、二つのピンに糸を張って、糸がたるまないようにして線を描くと、楕円が描ける」
テトラ「ああ、それは聞いたことがあります」
僕「うん、でも、この《カード》に書かれているような《積》が一定の場合は知らないなあ。曲線 $L$ はどんな曲線なんだろう……」
$PF_1\cdot PF_2$ という《積》が一定の点 $P$ が描く曲線 $L$ は、どんな曲線?
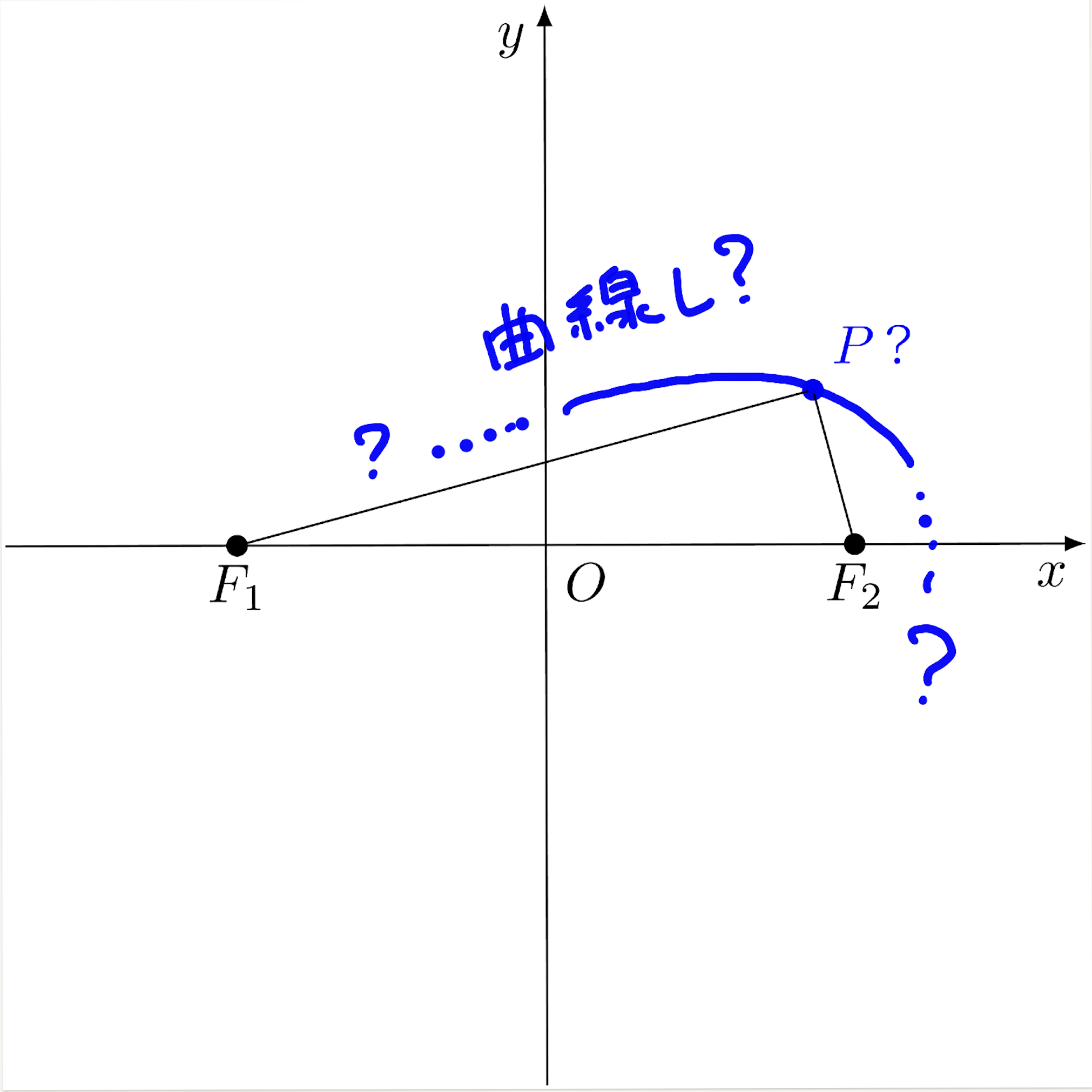
テトラ「はい。あたしも『$L$ って、どんな曲線になるんだろう』と思いました」
僕「線分 $PF_1$ と線分 $PF_2$ の長さの積が一定値 $a^2$ に等しい……つまり、こういうことだね」
$$ PF_1\cdot PF_2 = a^2 $$テトラ「そうです。あたしも、これと同じ式を立てて計算を進めていたんです……けれど、 まだ全然《わかった感じ》がしていません。そうだ! あたしがどんなふうに考えたか、 話を聞いていただけますか?」
僕「もちろん!」
テトラ「あたしはまず《カード》に書かれている二点 $F_1(-a, 0), F_2(a, 0)$ を描きました。 それから適当なところに点 $P$ を描いて、その座標を $P(x, y)$ と表すことにしました」
点 $F_1(-a, 0)$ と、点 $F_2(a, 0)$ と、点 $P(x, y)$
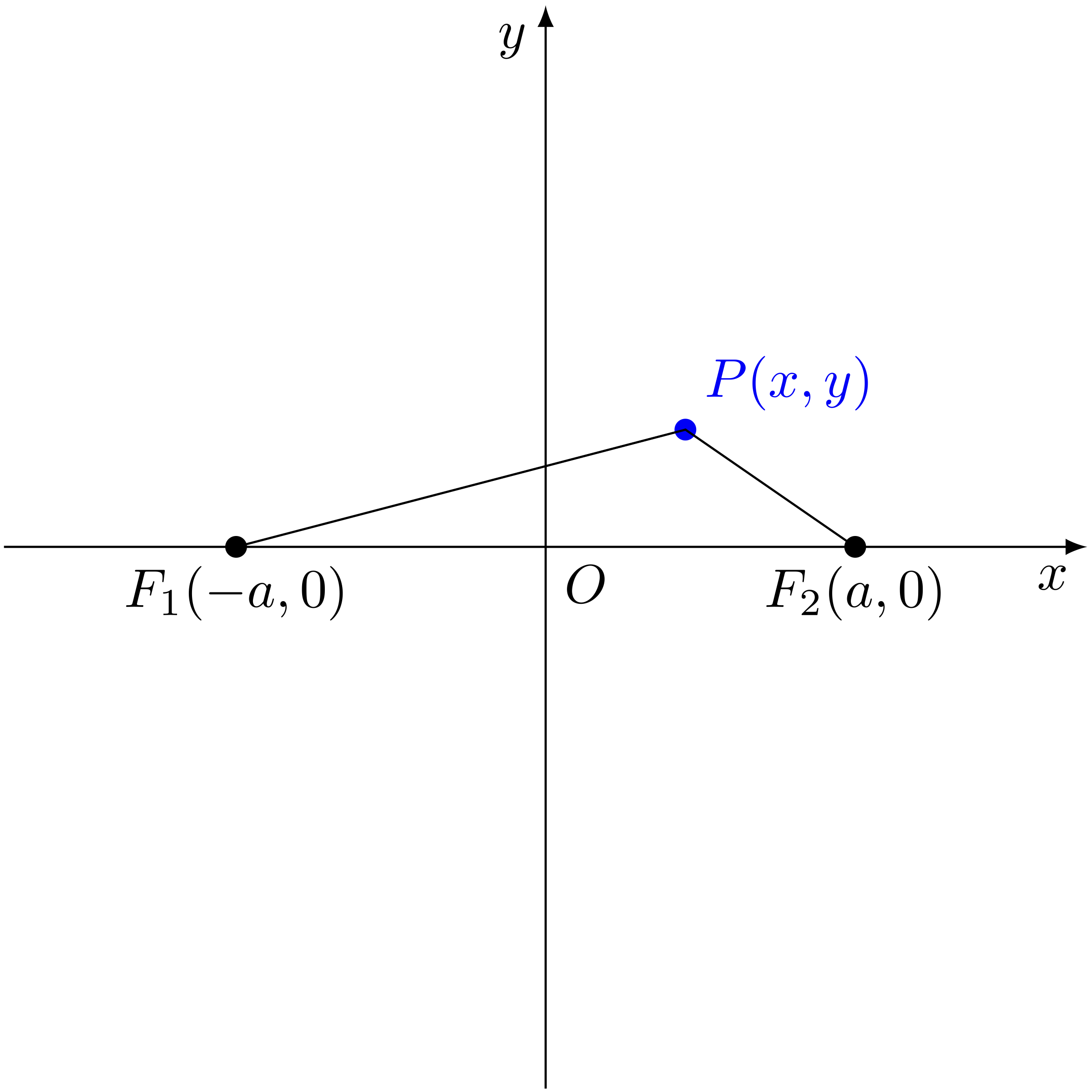
僕「うん、いいよ」
テトラ「それから、《カード》に書かれている条件を、 $a, x, y$ を使った数式で表そうと思いました」
僕「うんうん、自然な流れだ」
テトラ「先輩は先日、
数式で表現することは《お友達》になったしるしの一つ
とおっしゃってましたよね(第368回参照)。 だから、この点 $P$ や曲線 $L$ と《お友達》になるために数式で書こうと思ったんです」
僕「なるほど」
テトラ「《カード》に書かれている条件というのは、
《線分 $PF_1$ と線分 $PF_2$ の長さの積は $a^2$ に等しい》
というものですが、これはさっき先輩が書いてくださった、 $$ PF_1 \cdot PF_2 = a^2 $$ と式で表せます。ですからこの式を $x, y, a$ を使った式に書き換えていきます」
僕「うん」
テトラ「まず線分 $PF_1$ の長さは、 $$ PF_1 = \SQRT{(x - (-a))^2 + (y - 0)^2} $$ になります。ごちゃごちゃしてますけど、いまは勘違いしないようにわざと冗長に書いているんです」
僕「いやいや、よくわかるよ。点 $P(x, y)$ と点 $F_1(-a, 0)$ の距離だ。 ココとココに $-a$ と $0$ をそのまま入れたという意味だよね」
$$ PF_1 = \SQRT{(x - \FOCUS{(-a)})^2 + (y - \FOCUS{0})^2} $$テトラ「はいはい、そうです。また、線分 $PF_2$ の長さも同じように考えて、 $$ PF_2 = \SQRT{(x - a)^2 + (y - 0)^2} $$ になります。点 $F_2$ の座標は $(a, 0)$ だからです。 これで、 $PF_1 \cdot PF_2 = a^2$ は $x,y,a$ を使った式に書き換えることができます。 つまり…… $$ \begin{align*} PF_1 \cdot PF_2 &= a^2 \\ \SQRT{(x - (-a))^2 + (y - 0)^2}\cdot \SQRT{(x - a)^2 + (y - 0)^2} &= a^2 \\ \SQRT{(x + a)^2 + y^2}\cdot \SQRT{(x - a)^2 + y^2} &= a^2 \end{align*} $$ ……ということです」
線分 $PF_1$ と線分 $PF_2$ の長さの積は $a^2$ に等しい(点 $P$ が満たすべき条件)
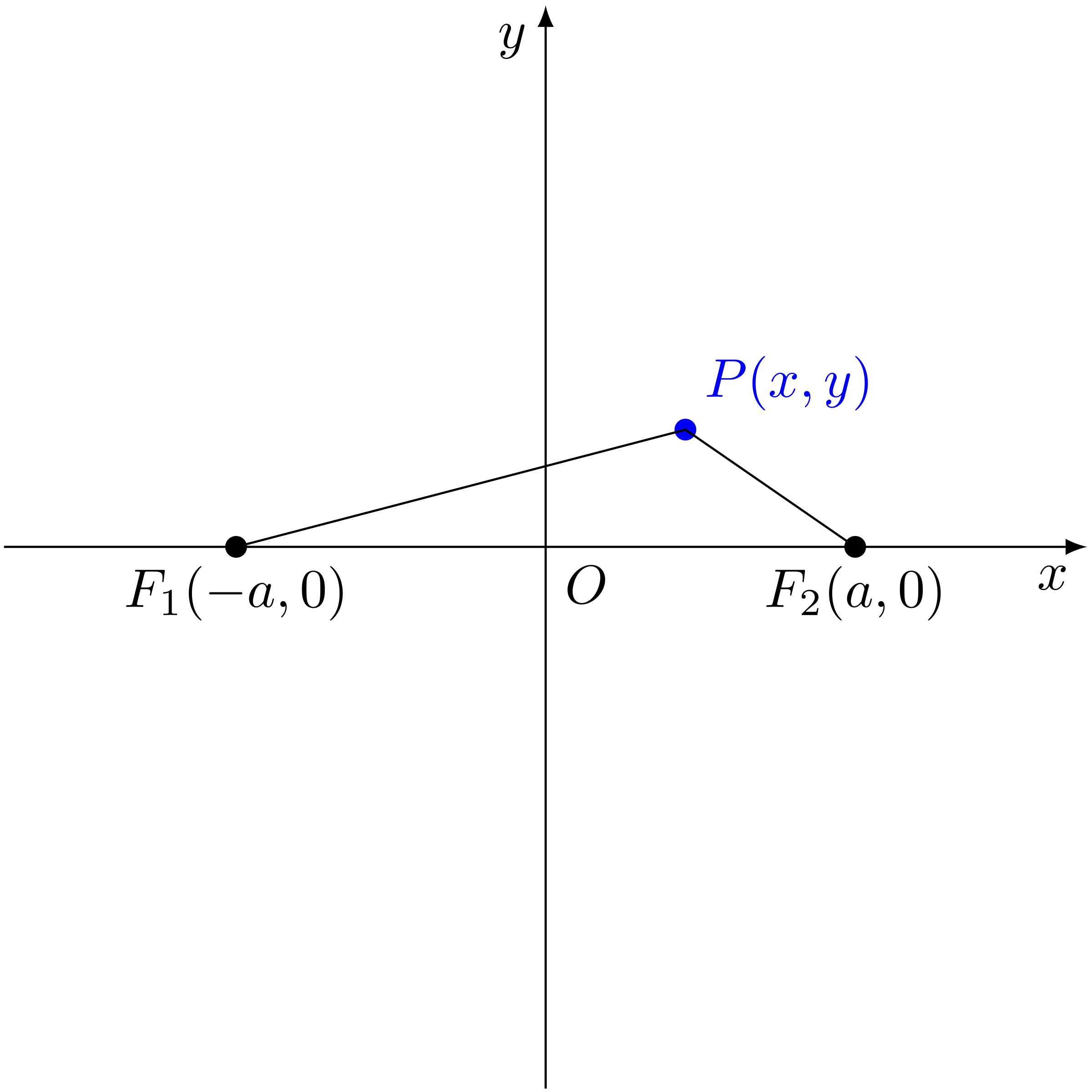
$$ PF_1 \cdot PF_2 = a^2 $$
$$ \SQRT{(x + a)^2 + y^2}\cdot \SQRT{(x - a)^2 + y^2} = a^2 \qquad \cdots\cdots\heartsuit $$
僕「うんうん。着々と計算が進んでいるね」
テトラ「はい。この $\heartsuit$ の式、 $$ \SQRT{(x + a)^2 + y^2}\cdot \SQRT{(x - a)^2 + y^2} = a^2 $$ で《カード》に書かれた条件はすべて表されていると思いました。 つまり、ポリア先生の《条件はすべて使ったか》という問いかけへの答えはYesです」
僕「おお!」
テトラ「それはいいんですが、 $\heartsuit$ の式を見てもさっぱり《わかった感じ》がしません。 なので——この左辺の式を計算することで、もっと簡単な式が作れるんじゃないかと思いました。 『$L$ って、そういう曲線なんですね!』 と声を上げたくなるような式です」
僕「そこで、計算を始めた……と」
テトラ「はい、そうです。 $\heartsuit$ の式全体に、 $x, y, a$ という文字が散らばっていますので、 計算を進めていって、文字を整理すれば《何か》がわかるはずだと思ったんです」
僕「すばらしいな!」
テトラ「き、恐縮です」
僕「テトラちゃんは、自分の考えた道筋を言葉にして表現できるんだね。 だから、いま話を聞いていて、テトラちゃんがどんなふうに考えたかがよくわかったよ」
テトラ「そんなこと言われると……何だか照れちゃいます」
僕「僕も、いまのテトラちゃんと同じように考えることがよくあるよ。 文字が散らばっていたり、式が整理されていなかったりするとき、 まずは式をちゃんと整理してみようと思うんだ。 そうすれば、きっと、面白いことが《何か》見つかるはずだと考える」
テトラ「はい……」
僕「それで、この $\heartsuit$ から計算を進めていったんだね」
$$ \SQRT{(x + a)^2 + y^2}\cdot \SQRT{(x - a)^2 + y^2} = a^2 \qquad \cdots\cdots\heartsuit $$テトラ「はいっ! そうです、そうです」
テトラちゃんは元気よくそう言うと、進めていた計算を見せてくれた。

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年9月16日)