![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
僕とテトラちゃんの《力学トーク》は続く。
回転運動をしているおもりのクイズ(第375回参照)を発端として、 遠心力という《見かけの力》について話していた(第376回参照)。 ニュートンの運動方程式が成り立つ慣性系と、 成り立たない非慣性系の関係を話し(第377回参照)、 等速円運動している質点の運動を定量的に追っていたところ(第378回参照)。
僕「うん。だから、等速円運動では、加速度ベクトルの《向き》は、回転中心を原点にした位置ベクトルの《向き》とは逆向きだとわかるよね? $-\omega^2$ は負だから」
等速円運動している質点の位置ベクトル $\vec x$ と、速度ベクトル $\vec v$ と、加速度ベクトル $\vec a$ の向き
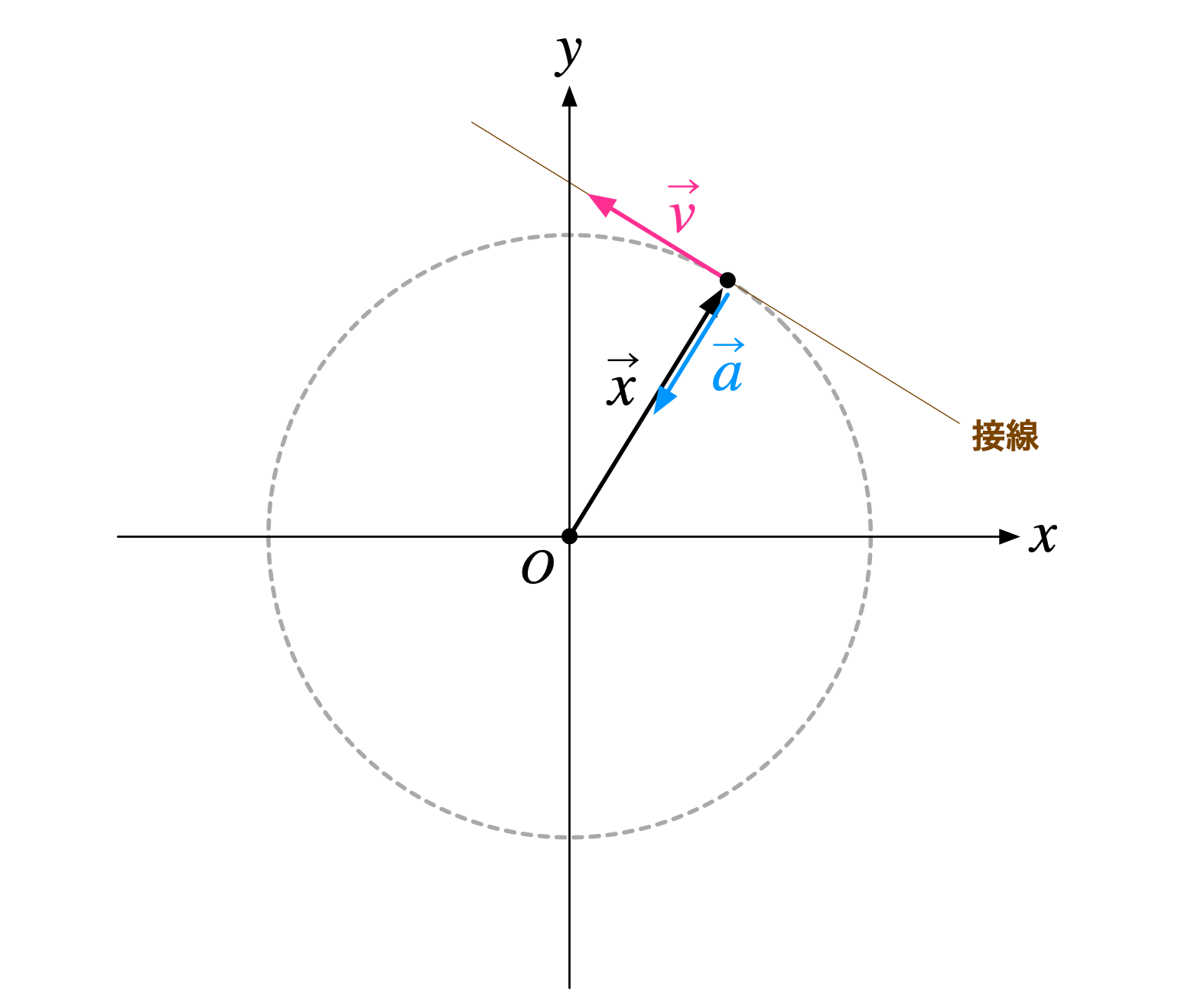
テトラ「加速度ベクトルの向きは、位置ベクトルの逆向き……あっ!!!! もしかしてこれって、 おもりに掛かる力が常に回転中心に向かっているということ?」
僕「まさに、そう! ニュートンの運動方程式から、加速度ベクトルの向きは力のベクトルの向きと一致する。 僕たちは、等速円運動している質点の位置から計算していって、 $$ \vec a = -\omega^2\vec x $$ を得た。これとニュートンの運動方程式 $\vec F = m\vec a$ から《等速円運動している質点に掛かる力は常に中心に向いている》ことが示されるんだよ!」
$$ \vec F = m\vec a = -m\omega^2\vec x $$テトラ「力 $\vec F$ と位置ベクトル $\vec x$ は逆向きになるから……なるほど、おもしろいです。本当におもしろいですっ!」
僕たちが話しているところに、ミルカさんがやってきた。
ミルカ「今日は何を話している?」
テトラ「あ、ミルカさん! 回転運動についてです。 等速円運動をしている質点の物理量の関係、それを計算していました。 これって、おもしろいですよね」
ミルカさんは肯いて、僕の方を向く。
ミルカ「君が好きそうな話だ。直線運動と円運動という《二つの世界》の対比、あるいは類比」
僕「そうだけど、ミルカさんも好きだよね」
ミルカ「嫌いではない」
テトラ「《二つの世界》の対比というのは、たとえば位置と角度のことですね? こんなふうに並べて見比べることができます」
ミルカ「ふむ」
テトラ「等速円運動を定量的に考えると、 速度ベクトル $\vec v$ を時刻 $t$ で微分して加速度ベクトル $\vec a$ が得られて、その向きを考えると、 質点に掛かる《力》のベクトルがちゃんと中心に向かうことが求められました(第378回参照)」
ミルカ「その対比を続けて《力》を考えるなら——直線運動で加速度を生むものを《力》だと考えたとき、円運動で《力》に対応するものは?」
テトラ「え? 力に何種類もあるんですか?」
ミルカ「そうではない。 速度を変化させることに寄与する物理量を《力》だと考えるなら、 角速度を変化させることに寄与する物理量は何か、という問いだ。 《二つの世界》の対比を続けて、速度に角速度を対比させたとき、 《力》に対比する物理量は何か」
テトラ「……でも、すでに力が回転に寄与しているのはわかっています。 たとえば糸から質点に掛かる力だけですよね?」
僕「求心力だね」
ミルカ「等速円運動における求心力は、速度の《向き》を変えることには寄与するが、 速度の《大きさ》を変えることには寄与していない。 同じことだが、角速度の変化には寄与していない」
テトラ「……そうですね。等速円運動では速さは一定ですし、角速度も一定です。 $v = r\omega$ ですから」
僕「たとえば角速度 $\omega$ がだんだん大きくなっていくような運動を考えるってことだよね。 そのときには質点の速さ $v = r\omega$ もだんだん大きくなっていく。だからその要因はもちろん《力》なんだけど、 直線運動と円運動の対応を意識して答えるなら、角速度に寄与するのは、もちろん——答えてもいいのかな?」
テトラ「あ、はい。お願いします」
僕「それは力のモーメントだよね! 回すことに寄与する《力》に相当するものは《力のモーメント》になる(第373回参照)」
テトラ「《力のモーメント》……力のモーメントというのは、距離と力の積でしたっけ?」
僕「そうだね。まず、回転運動を考えるときは《回転軸》、 つまり回転の中心を決めておく。テコでいうなら《支点》だね。 その上で《回転軸からの距離》と《回転に寄与する力》の積を考える。 その積が力のモーメントになる」
テトラ「はい……」
僕「テコの原理の図で、棒が回り出さないのは力のモーメントの総和がゼロになるとき(第373回参照)」
棒が回りださない条件
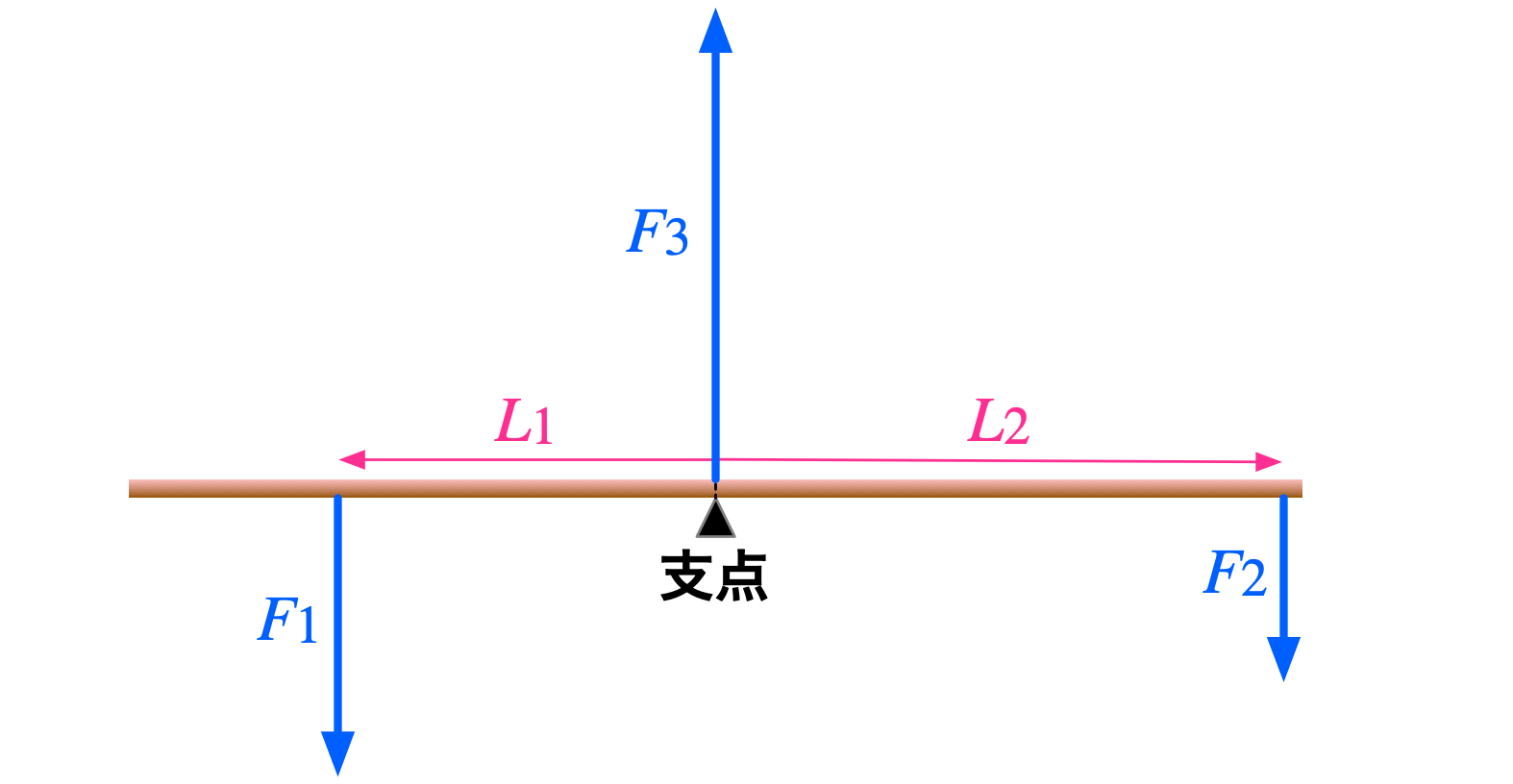
力のモーメントの総和が $0$ のとき、静止している棒は回り出さない。 $$ F_1L_1 - F_2L_2 + F_3L_3 = 0 $$ ($L_3 = 0$ に注意)
テトラ「はい。その《力のモーメント》が回転に寄与する力に相当する物理量なんですね? ……ちょっとまだ、《力》と《力のモーメント》が、心にうまく収まっていないみたいです」
ミルカ「対比を強調して考えるときには《力のモーメント》は《トルク》と一単語で呼んだ方がわかりやすい」
テトラ「トルク……」
ミルカ「《トルク》というのは《力のモーメント》の別名だ。 テコが動かないのはトルクの和がゼロになるとき。 なぜ《力》と別に《トルク》を考えるかというと——」
僕「物理量として便利だからじゃない?」
ミルカ「そういうこと。 直線運動を考えるときに《力》が重要な役割を果たすのと同じように、 回転運動を考えるときには《トルク》が重要な役割を果たす」
テトラ「トルク……って英語ですよね。スペルは?」
ミルカ「torqueだ。t-o-r-q-u-e」
テトラちゃんは辞書を引く。
テトラ「回すための力。ねじる力」
ミルカ「辞書で言葉の意味を調べるのはいいが、それに縛られないように」
テトラ「はい、それはわかっている……つもりです。 あたし、言葉の意味に引っ張られ過ぎるときがあるのは自覚があります」
僕「《力のモーメント》つまり《トルク》の僕の理解はこうだよ。 直線運動を考えるときは、力をそのまま扱うだけでいい。 回転運動を考えるときにも、力をそのまま扱ってもいい。 だけど、回転軸からの距離を考慮した物理量、つまりトルクを考えた方が便利なことがある」
テトラ「トルクを考える?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年12月16日)