![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
僕とテトラちゃんの《力学トーク》は続いている。
いまはテトラちゃんがまちがったという物理学のクイズ、 すでに正解は出ているけれど、 その理由について議論をしているところ。
クイズ(再掲)(第375回参照)
図のように、糸の付いたおもりが滑らかな机の上で一定の速さで円を描いて回転しています。
固定点には机にピンが打ってあり、糸はおもりと固定点にあるピンを結んでいます。
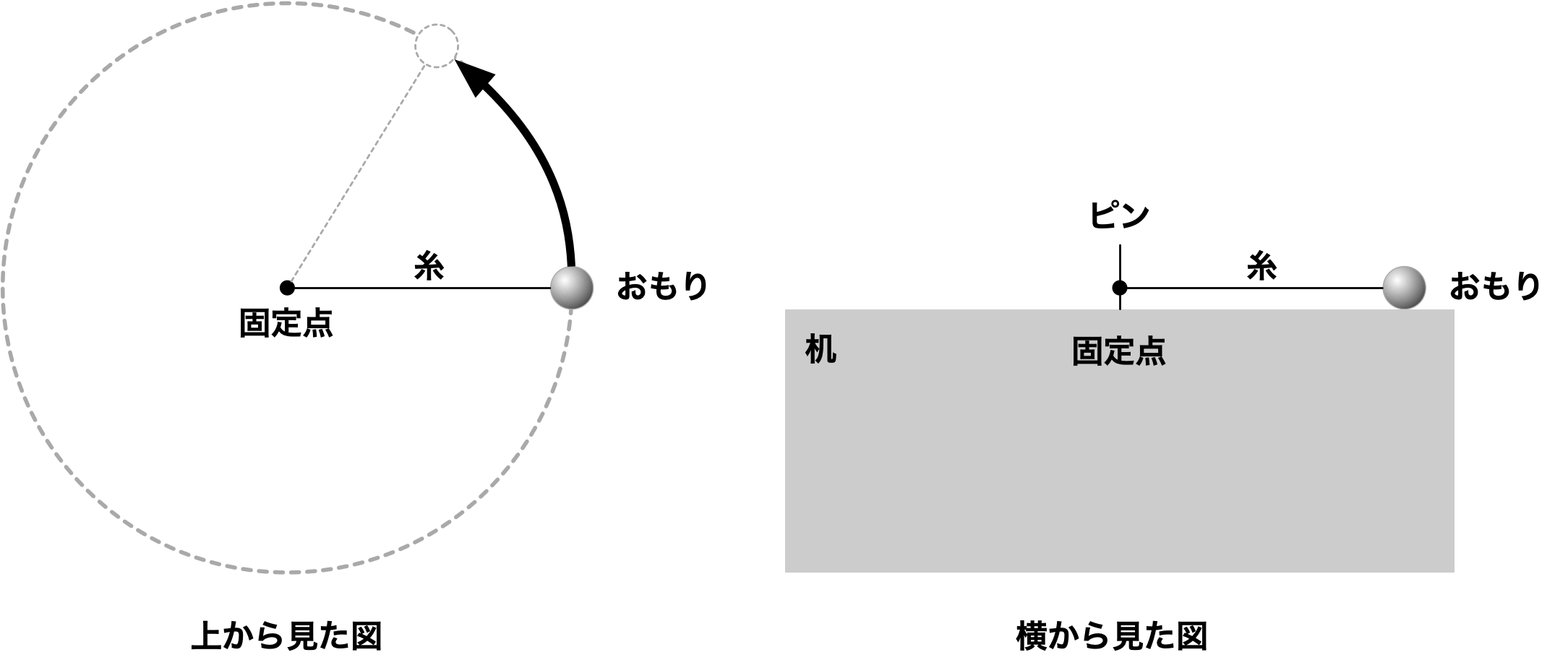
さて、ある瞬間に糸が切れたとします。切れた瞬間の位置から、おもりはどの向きに飛んでいくでしょうか。

糸の伸び縮み、空気の抵抗、糸とピンの摩擦、机とおもりの摩擦は考えないものとします。

クイズの答え
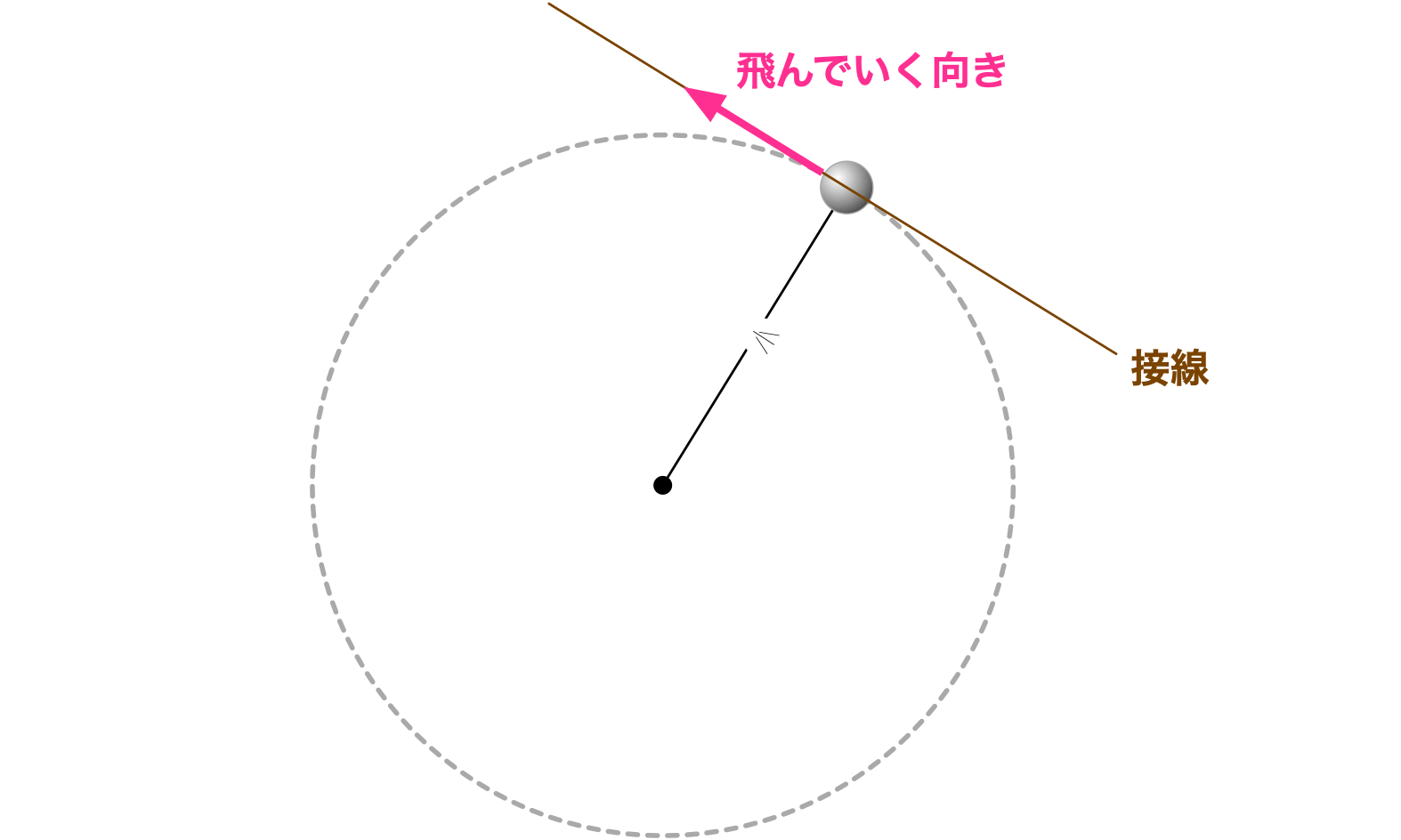
いま、僕とテトラちゃんは糸が切れる前におもりに働く力をすべて見つける考察を済ませ、 最後にはたった一つの力が残った。糸からの張力だ(第375回参照)。
僕が、遠心力は《見かけの力》だと伝えると、テトラちゃんはショックを受けた。
糸からおもりに働く力

テトラ「……あたしには、どこがおかしいか、まだわからないようです。 遠心力がないと言われると、かなりショックです」
僕「いや、遠心力という概念がないわけじゃないよ。説明を続けていけば《見かけの力》として、ちゃんと出てくる」
テトラ「遠心力は……見かけの力?」
僕「そうだね。でも《見かけの力》について話す前に、 まずは《糸からおもりに働く力》だけで回転運動していることをちゃんと理解しないとね」
テトラ「はい……あたしは《糸からおもりに働く力》だけなら、 おもりはピンのある固定点に向かうんじゃないかと考えてしまうんです。 だから、反対方向の力がある……つまり遠心力があると思ってしまいます」
僕「うん。あのね……もしもおもりが静止していたとしたら、 《糸からおもりに働く力》によっておもりはピンのある固定点に向かって動き始めることになる。 それはそうだよ。でも、このおもりは回転運動をしている。 つまりこのおもりは、円の接線方向への速度を持っているわけだ。 それが大きな違いになる」
テトラ「あたし……おもりが回転運動しているときに、 何が起こっているかうまく言えませんね」
僕「おもりが回転運動をしているときに何が起きているのか。 それは物理量を表す言葉で表現できる。 いまから、おもりの運動をあらわすためにいろんな言葉を再確認していこうか。 まずは、位置と速度から。どちらもベクトルで表せるから、位置ベクトルと速度ベクトルになる」
テトラ「はい……」
僕「時刻ごとに、おもりには位置がある。 この時刻にはこの位置にあり、別の時刻には別の位置にある。 このおもりの場合には、位置は二次元ベクトルで考えることができる。 時刻 $t_1$ の位置は $\vec x_1$ で、時刻 $t_2$ の位置は $\vec x_2$ のようにね」
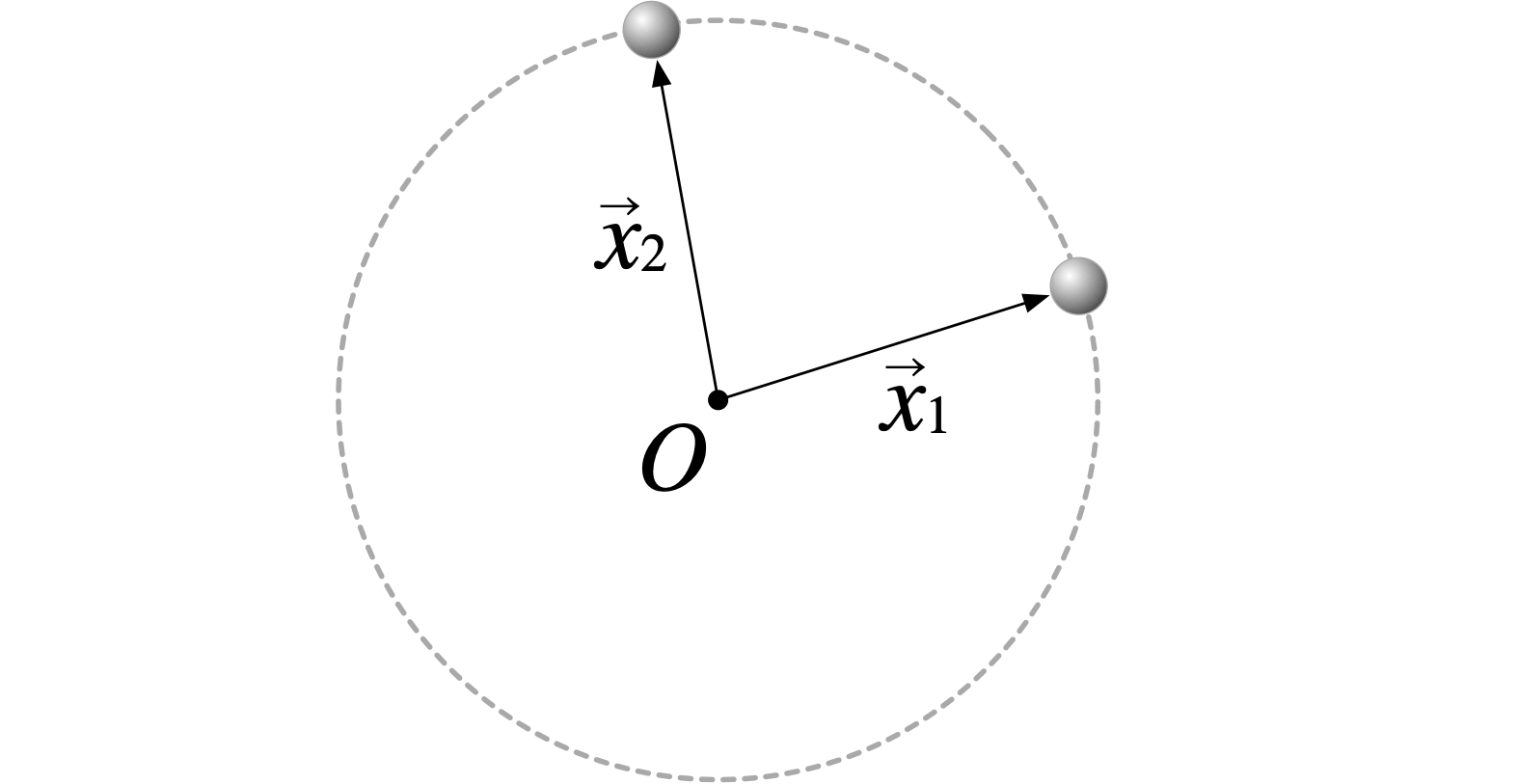
テトラ「はい、それは大丈夫です。原点をピンの位置に取ったわけですよね?」
僕「うん、そうそう。 そして、時刻 $t_1$ から時刻 $t_2$ までの《平均の速度》は《変位を掛かった時間で割ったもの》になる。 変位というのは位置ベクトルの変化のことで、これもベクトル。つまり変位ベクトルだね。 変位ベクトルは、 $$ \vec x_2 - \vec x_1 $$ で、その変化に掛かった時間は、 $$ t_2 - t_1 $$ なので、平均の速度は $$ \frac{\vec x_2 - \vec x_1}{t_2 - t_1} $$ になる。平均の速度もベクトルだよ」
テトラ「えっと……ちょっと自信がなくなってきました」
僕「《向き》と《大きさ》があるものはぜんぶベクトル。位置も変位も速度もすべてベクトル」
テトラ「は、はい……」
僕「具体的に変位ベクトルの図を描いてみようか。時刻 $t_1$ と $t_2$ における位置の変化というのは、 要するにこういうベクトルのこと。これが変位ベクトル $\vec x_2 - \vec x_1$ になる」
変位ベクトル $\vec x_2 - \vec x_1$

テトラ「あ、ベクトルの差だからそうなりますね。 そして変位という気持ちもわかりました。 時刻 $t_1$ のとき位置から時刻 $t_2$ の位置までの矢印で、 位置がどう変わったかを表しているんですね」
僕「そうだね。ここまでが変位ベクトルの話」
テトラ「はい」
僕「そして、ここから速度ベクトルの話。 速度ベクトルの向きに関してはこの変位ベクトルの向きと同じでいいんだけど、 速度ベクトルの大きさ——つまり速さ——については、 この変位ベクトルの大きさを掛かった時間で割る。 だからたとえば、こんな矢印のようになる。向きは変位ベクトルと同じだけど、長さが違う」
平均の速度ベクトル $(\vec x_2 - \vec x_1)/(t_2 - t_1)$
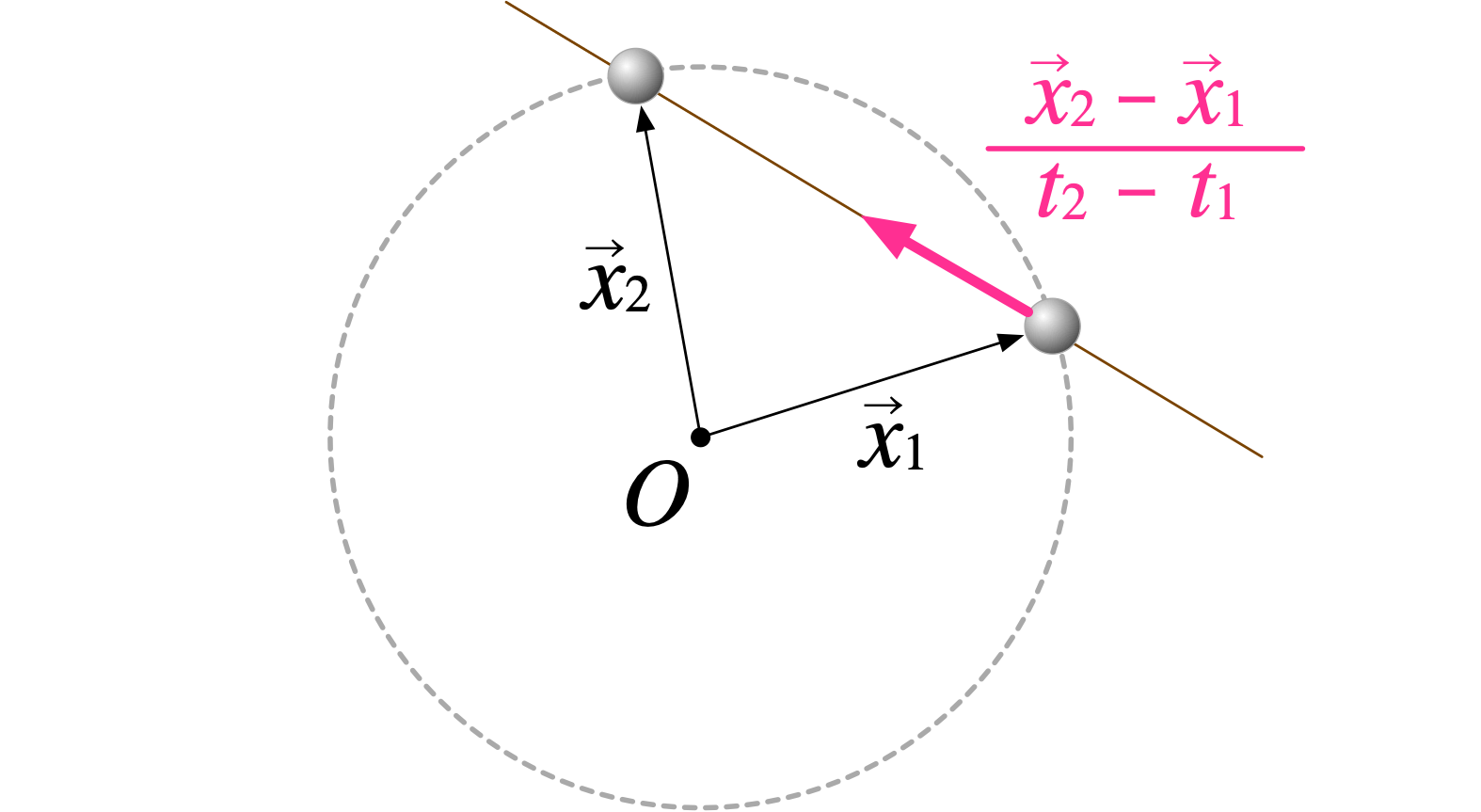
テトラ「でも、おもりがこんなふうに斜めにジャンプするわけではない……ですよね?」
僕「そうだね。おもりが斜めにジャンプするかのように見えるのは、時刻 $t_1$ と時刻 $t_2$ のようにジャンプした二つの時刻で考えたから」
テトラ「ははあ……」
僕「実際に回転運動しているおもりは瞬間瞬間に進む向きを変えている。 だから $t_2 - t_1$ が大きくなると、実際の動きとのずれも大きくなる。 そこで数学が出てくる」
テトラ「もしかしてですけど……極限が出てきますか?」
僕「そうそう! $t_2$ を $t_1$ に近づけていったとき、平均の速度ベクトルはどのようなベクトルに限りなく近づくかという極限を考えることになる。 ちゃんとテトラちゃんは重要概念をおさえているね」
テトラ「き、恐縮です」
僕「時刻 $t_2$ を、時刻 $t_1$ に近づけたとき 平均の速度ベクトルが限りなく近づくベクトル。それが、時刻 $t_1$ における瞬間の速度ベクトルになる。 それは結局、おもりの変位ベクトル $\vec x$ を時刻 $t$ で微分する計算になるわけだけど……でも、 図で見るとかなり直感的にわかるよ」
テトラ「?」
僕「というのは、 $t_2$ を $t_1$ に近づけていくようすをこんなふうに描いてみれば、 $t_1$ における瞬間の速度ベクトルは接線方向になると想像がつくから」

テトラ「はい、はい、そうです。そもそも接線というのがそういうものでしたし、あたしが極限というキーワードを思い出したのも、 こういうイメージがあったからです……」
僕「と、ここまでが、おもりが持っている速度ベクトルの話。数式できちんと示したわけではないけれど、 回転運動しているおもりの位置ベクトルと速度ベクトルがどんな様子をしているかの説明」
そこでテトラちゃんが手を挙げる。
テトラ「確認したいことがあります」
僕「はいはい、どうぞ」
テトラ「速度ベクトルはおもりの位置が変われば変わりますよね?」
僕「うん、もちろん。一定の速さで回転運動しているおもりだから、速度ベクトルの《大きさ》はいつも一定だけど、 速度ベクトルの《向き》は時々刻々変わっていくよ。そして一回転したら、最初の向きと同じ向きになっている」
テトラ「ちょ、ちょっとしつこくてすみませんが、もう一つ確認してもいいですか」
僕「どうぞどうぞ」
テトラ「おもりの位置ベクトルも刻々と変わりますよね。そして一回転したら最初の向きと同じ向きですね?」
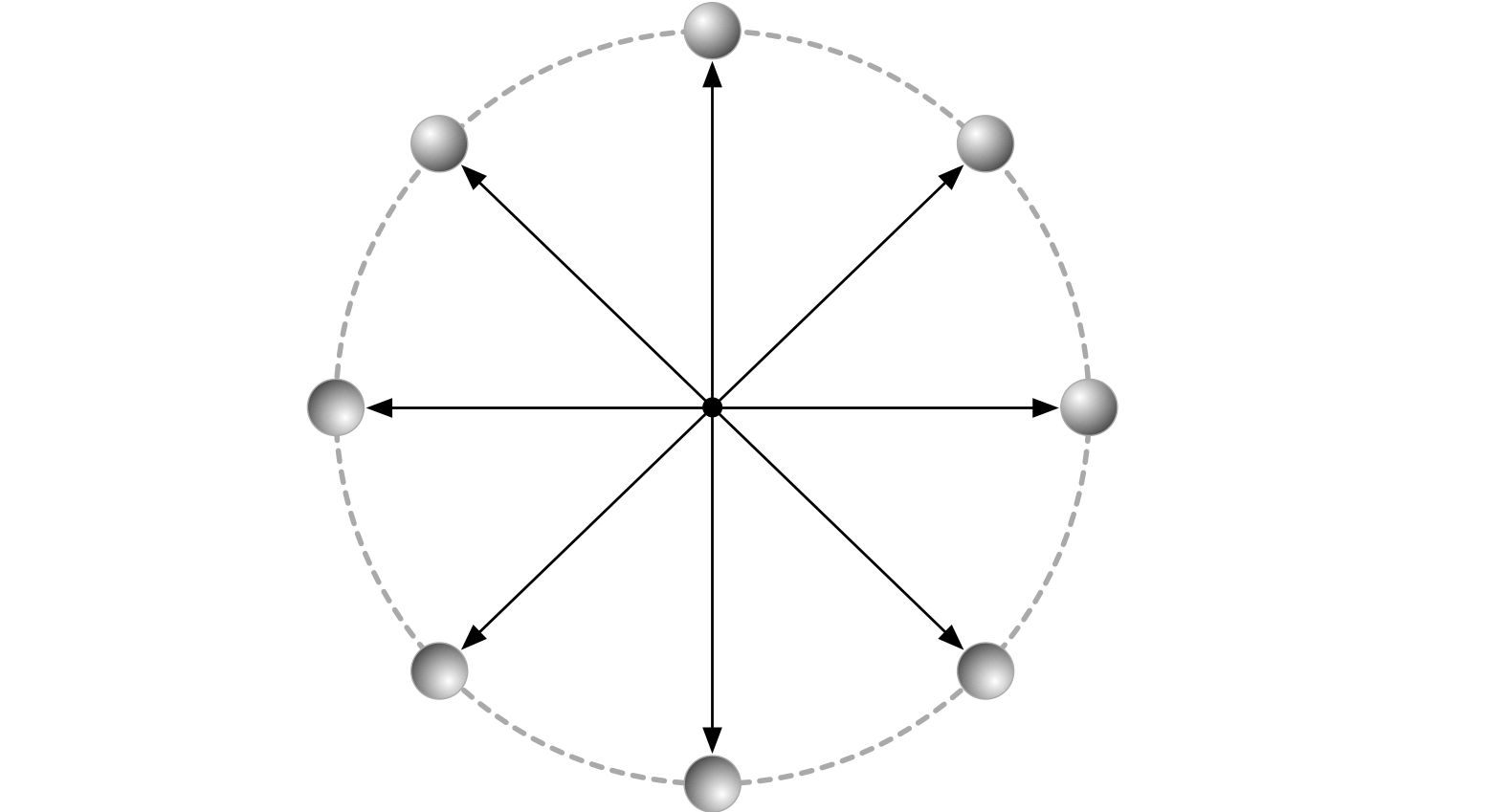
僕「そうそう。いまは固定点を原点に取っているから、 位置ベクトルの《大きさ》はいつも一定。この円運動の半径そのものになる。 でも位置ベクトルの《向き》は時々刻々変わっている」
位置ベクトルの変化のようす
速度ベクトルの変化のようす
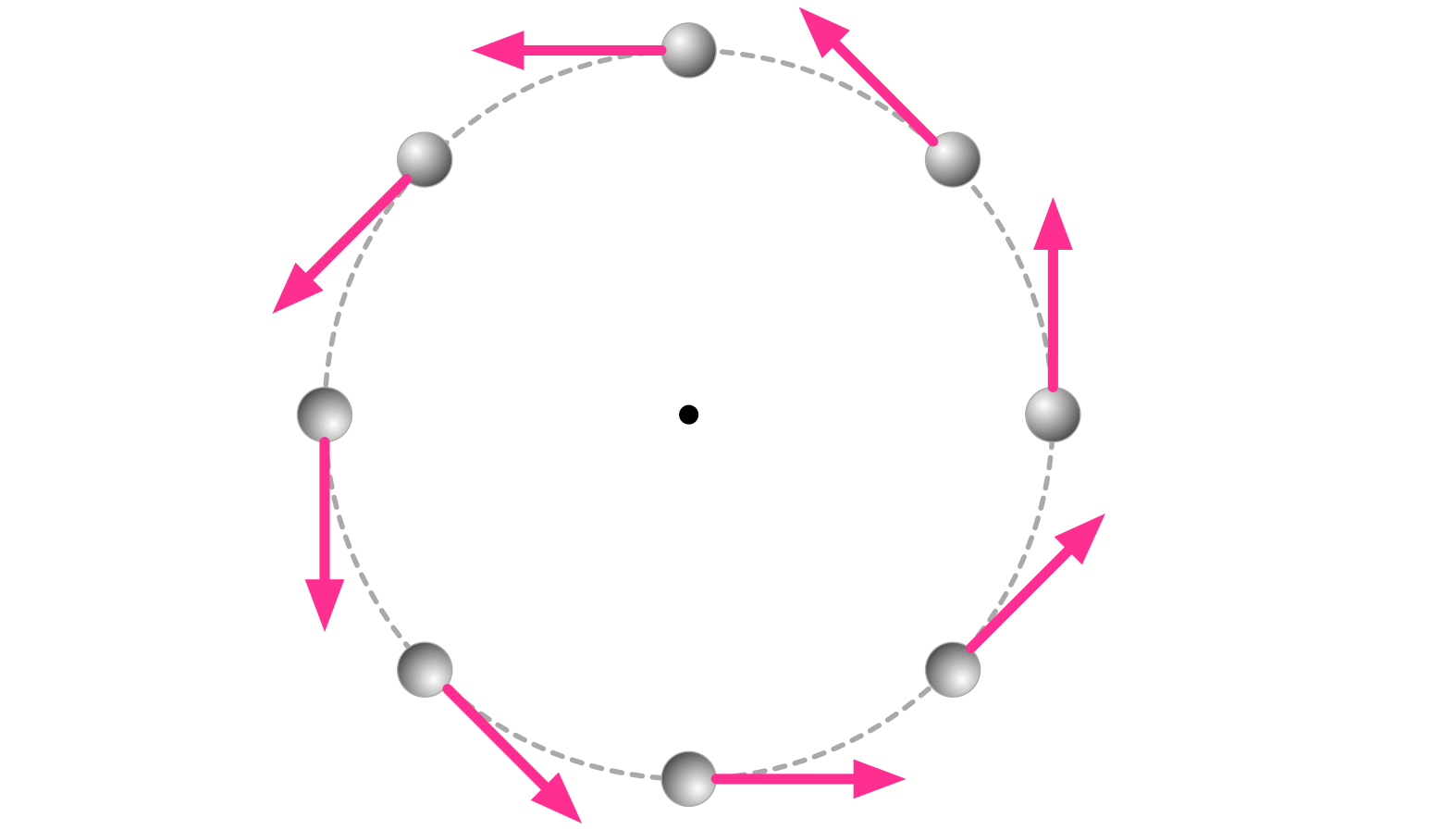
テトラ「はい……はい……ここまで、あたしは理解していると思います。 一定の速さで円運動をしているおもりがあって、位置ベクトルの変化と速度ベクトルの変化、どちらも想像できています」
僕「いいね! あとは力との関係を押さえればいい!」
テトラ「力との関係……」
僕「ニュートンの運動方程式で表される運動の法則だね。それは力と加速度の関係を表している」
運動の法則(ニュートンの運動方程式)
質量が $m$ の質点に対して力 $\vec F$ が掛かっているとき、 質点の加速度を $\vec a$ とすると、 $$ \vec F = m \vec a $$ が成り立つ。
テトラ「はい。ニュートンの運動方程式については知っていますが……知っていると思いますが……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年11月25日)