第377回 シーズン38 エピソード7

「回る」と「回す」（前編）

図書室にて

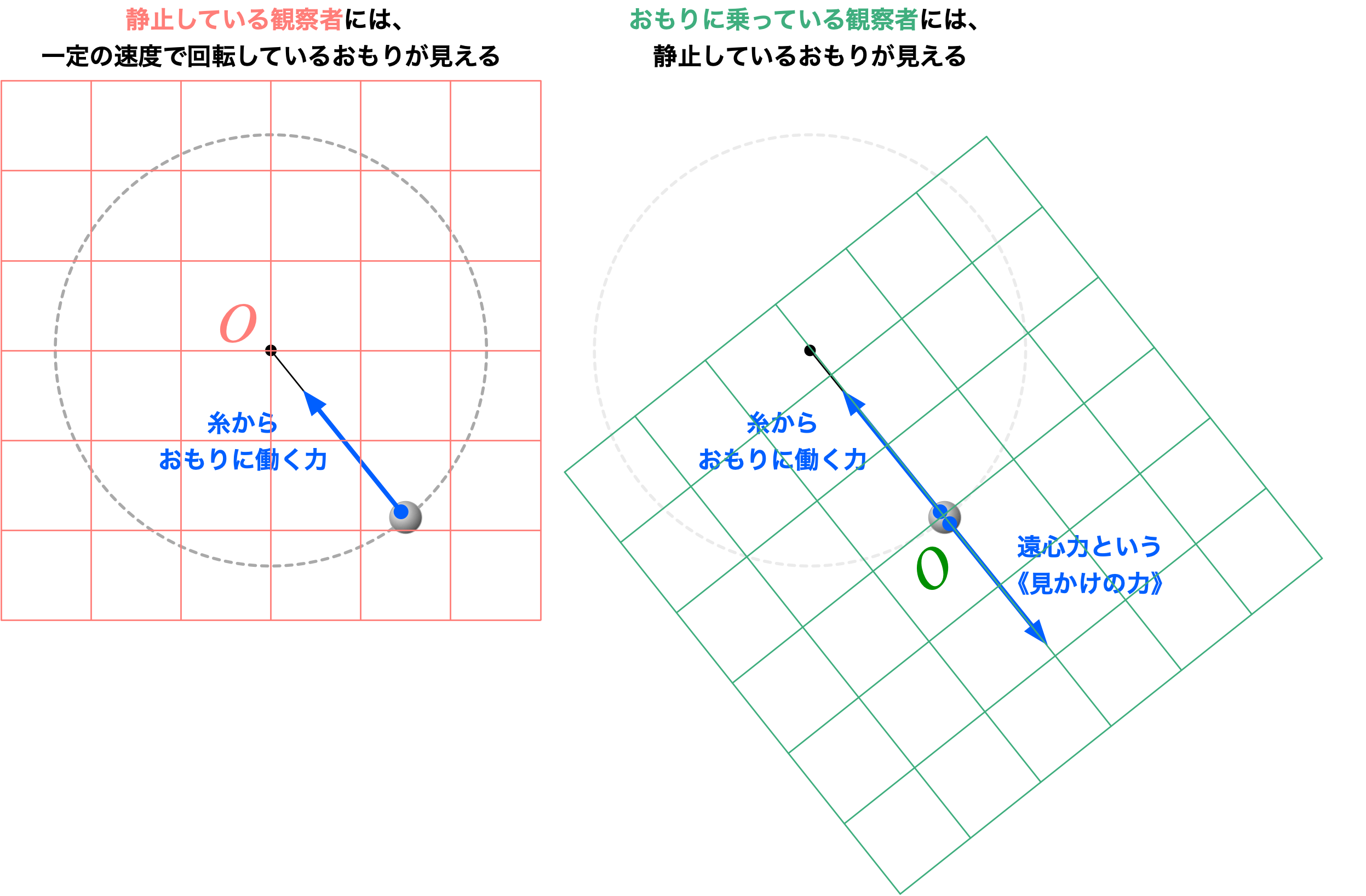
テトラ「……なるほどです！　いま、初めてあたし《見かけの力》の意味がわかったように思いますっ！」

僕「それはよかった。もう一つは？」

テトラ「もう一つ？」

僕「二つの疑問のもう一つ」

テトラ「ああ、はい。あのですね。先ほど先輩がおっしゃった《便利》という言葉に引っかかりました」

僕「遠心力という力が働いていると考えると非常に便利」

テトラ「それです！　便利ってどういうことでしょう」

僕「それははっきりしているよ。ニュートンの運動方程式が使えて便利という意味」

テトラ「？？？？」

僕「ど、どうしたの？」

テトラ「だってそれでは……それではまるでニュートンの運動方程式が使えるときと使えないときがあるみたいに聞こえたので」

僕「うん、そうだよ。 $\vec F = m \vec a$ というニュートンの運動方程式は、 《静止しているか、等速直線運動している座標系》——慣性系（かんせいけい）——でのみ使えるんだ」

テトラ「！！！！」

テトラ「ニュートンの運動方程式は、 座標系によって成り立ったり成り立たなかったりするんですか……成り立たない場合があるなんて、 そんなの、想像したこともなかったです！」

僕「だから《加速度運動している座標系》——非慣性系（ひかんせいけい）——ではそのままではニュートンの運動方程式は使えない。 だから、回転している座標系で考えているときは、ニュートンの運動方程式は使えない。 たとえば、おもりに乗っている座標系の場合のことだね（第376回参照）」

テトラ「……そうなんですね」

座標系自体の加速度から《見かけの力》へ

僕「でもすべてがめちゃくちゃになるわけじゃないよ。 ニュートンの運動方程式に出てくる加速度は《観測されている加速度》だけど、 そこに《座標系自体の加速度》 の項を付け加えればいい」

テトラ「加速度を付け加える？」

僕「うん、座標系自体が持つ加速度を加味して、《見かけの力》が働いていると考えるなら、 非慣性系でも、ニュートンの運動方程式が最初から成り立っているかのように式を立てることができる。 そこが《見かけの力》の便利な点」

テトラ「え……よくわかりませんでした」

僕「じゃ、ちゃんと式で書いて説明するね。 通常のニュートンの運動方程式は、 $$ \vec F = m \vec a $$ という式だけど、 もしも、この加速度 $\vec a$ が《加速度運動している座標系》、つまり非慣性系で表したものだとすると、この式は成り立たない」

テトラ「はい。おもりに乗っている人の座標系……ですね」

僕「そうそう。そこで《加速度運動している座標系》自体の加速度を $\vec A$ とする。 静止している観測者が《回転するおもりに貼り付けたグラフ用紙》を見たときの加速度をイメージすればいいね（第376回参照）。 そうすると、ニュートンの運動方程式は、 $$ \vec F = m (\vec A + \vec a) $$ になる。これは静止している人が見た状況、つまり慣性系なので成り立つ」

テトラ「ああ……」

僕「だから、この式を展開してやると、 $$ \vec F = m \vec A + m \vec a $$ となる。ここで $m \vec A$ という式はちょうど《質量×加速度》という形だから、あたかも《力》であるように見なせることがわかる」

テトラ「力と……見なせる」

僕「そこで、 $m \vec A$ を移項する。加速度の側から力の側に移すんだ。 移項と言っちゃったけど、移項することに特別な意味はないよ。単に等式の両辺に $- m \vec A$ を加えただけで、物理的に特別なことをしたわけじゃない。 力と見なすことを強調したいだけのこと。そこで $- m \vec A$ が《見かけの力》になる。たとえば、僕たちが考えてきた遠心力がこの《見かけの力》になる（第376回参照）」

テトラ「何だか、あれよあれよという間に《見かけの力》が出てきました……」

僕「そして、この式は確かに $$ \overbrace{\vec F + \underbrace{(- m \vec A)}_{\textbf{見かけの力}}}^{\textbf{おもりに働くすべての力}} = m \vec a $$ となって、ニュートンの運動方程式の形になっている。 これが『《見かけの力》を考えることによって、ニュートンの運動方程式が使えて便利』という話の流れだね」

テトラ「あの……式変形は移項だけでしたから何も難しくありませんし、《見かけの力》と見なす部分もよくわかりました。 でも、一つだけわからないのが、最初のこの式です。 $$ \vec F = m (\vec A + \vec a) $$ これはどこから出てきたんでしたっけ？」

僕「ああ、これは簡単だよ。加速度は速度を $t$ で微分したものだし、速度は位置を $t$ で微分したものだよね」

テトラ「は、はい。 $t$ は時刻ですね？　位置を $t$ で微分して速度、速度を $t$ で微分して加速度。はい、それは理解しています」

僕「いまは位置も速度も加速度もベクトルだけど、話としては同じ。成分ごとに微分するだけのことだから」

テトラ「はい」

僕「いま、位置 $\vec x$ というのは、加速度運動している座標系での位置と考える。 たとえば、おもりの位置だとすると $\vec x$ は原点にじっとしているわけだ」

テトラ「ああ……はいはい。そうですね。おもりはぐるんぐるん回っていますけど、 おもりの上に貼り付けたグラフ用紙——加速度運動している座標系——で調べると、 おもりは原点でじっとしています。貼り付けてるので！」

僕「そういうこと。もちろんおもり以外のものすべての位置も $\vec x$ で表せる。 その位置 $\vec x$ は、あくまでおもりに貼り付けたグラフ用紙を使って表すことになる」

テトラ「はい、わかります。おもりに乗ったつもりになってあたりを見たとき、まわりにあるものの位置が $\vec x$ ですね」

僕「そうそう。さてそこで《静止している座標系》に対して《加速度運動している座標系》自体の位置を $\vec X$ とする。 この $\vec X$ は静止している観測者が見た位置だよ。図にした方がいいね。こういうイメージ」

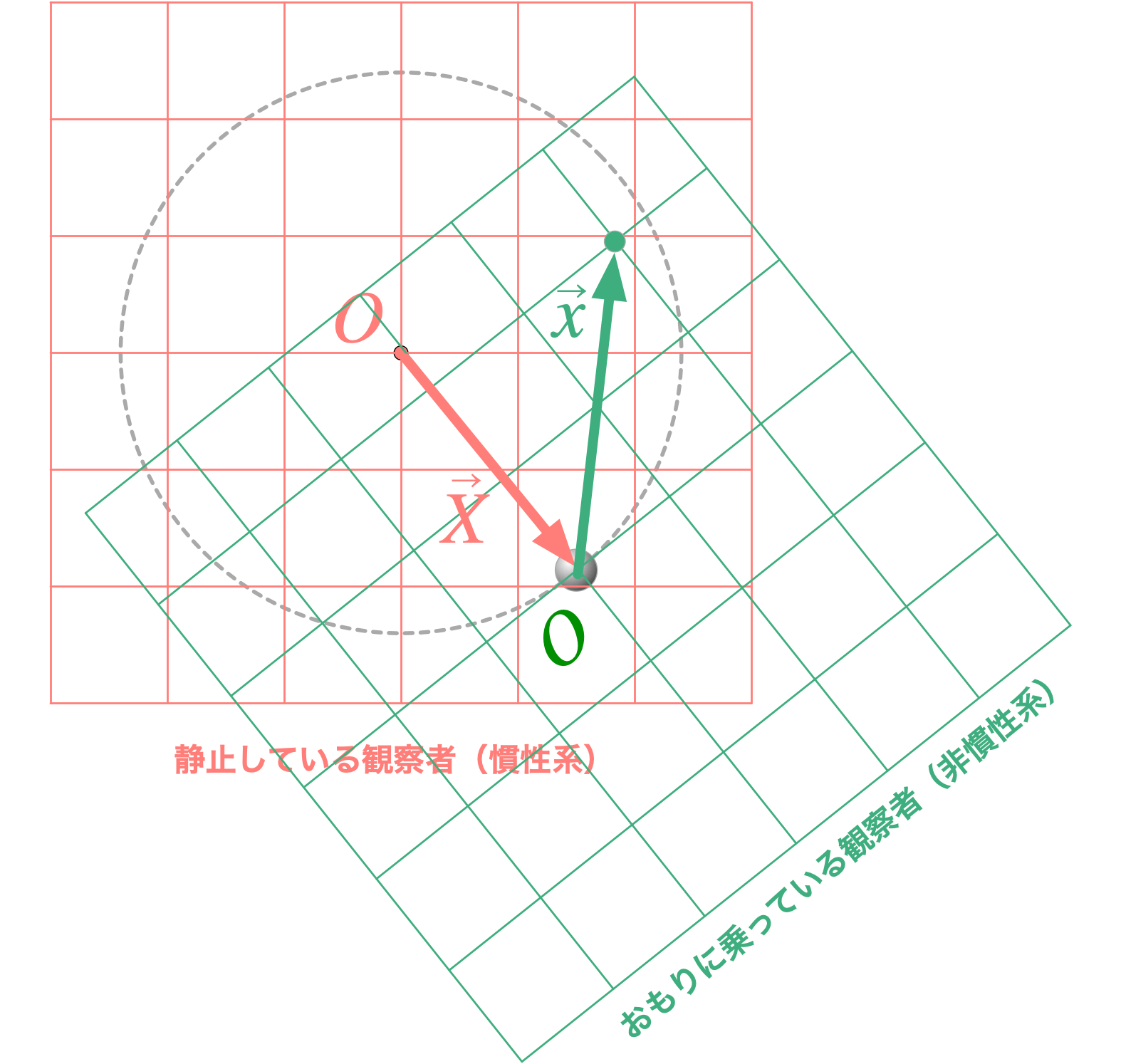
テトラ「はい」

僕「加速度運動している座標系での位置 $\vec x$ は、 $$ \vec X + \vec x $$ としてやれば、静止している座標系における位置に座標変換できることになる」

テトラ「はいはい。矢印をつないで考えるわけですね。わかります」

僕「そうそう。《加速度運動している座標系自体の位置》を加えてやれば、《静止している座標系における位置》がわかる。それが、 $$ \vec X + \vec x $$ だね。 これが位置。位置を $t$ で微分したものが速度だけど、微分は線形性を持っているから、 $$ \frac{d}{dt}(\vec X + \vec x) = \frac{d}{dt}\vec X + \frac{d}{dt}\vec x $$ となる」

テトラ「あ……えっと、これは、 $$ (\vec X + \vec x)' = (\vec X)' + (\vec x)' $$ と同じですよね？《和の微分は微分の和》」

僕「そうだね。 $\prime$ を《時刻 $t$ の微分》であることを忘れなければ、それでいいよ。 それで書くなら、加速度は、 $$ \begin{align*} (\vec X + \vec x)'' &= ((\vec X + \vec x)')' \\ &= ((\vec X)' + (\vec x)')' \\ &= (\vec X)'' + (\vec x)'' \\ &= \vec A + \vec a \end{align*} $$ になる。つまり、 $$ (\vec X + \vec x)'' = (\vec X)'' + (\vec x)'' = \vec A + \vec a $$ となる」

テトラ「ははあ、なるほど。わかってきました」

僕「ニュートン運動方程式は、静止している座標系で見て、 $$ \vec F = m (\vec X + \vec x)'' $$ になる。微分の線形性を使うと、 $$ \vec F = m ((\vec X)'' + (\vec x)'') $$ がいえる。だから結局、 $$ \vec F = m (\vec A + \vec a) $$ と書けることがこれでわかったね。これがスタートポイントだったんだ」

テトラ「わかりました！　あたしの理解したことはこうですっ！」