$
\newcommand{\TEXT}[1]{\textbf{#1}}
\newcommand{\REMTEXT}[1]{\textbf{#1}}
\definecolor{CUD-GREEN}{rgb}{0.012,0.686,0.478}% 3,175,122
\newcommand{\MARK}[1]{\textcolor{red}{#1}}
\newcommand{\MARKA}[1]{\textcolor{red}{#1}}
\newcommand{\MARKB}[1]{\textcolor{blue}{#1}}
\newcommand{\MARKC}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\GEQ}{\geqq}
\newcommand{\LEQ}{\leqq}
\newcommand{\NEQ}{\neq}
\newcommand{\FOCUS}[1]{\fbox{ $#1$ }}
\newcommand{\REDFOCUS}[1]{\textcolor{red}{#1}}
\newcommand{\GREENFOCUS}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUEFOCUS}[1]{\textcolor{blue}{#1}}
\newcommand{\BROWNFOCUS}[1]{\textcolor{brown}{#1}}
\newcommand{\REDHEART}{\REDFOCUS{\heartsuit}}
\newcommand{\REDTEXT}[1]{\textcolor{red}{#1}}
\newcommand{\GREENTEXT}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUETEXT}[1]{\textcolor{blue}{#1}}
\newcommand{\ABS}[1]{|#1|}
\newcommand{\PHANTOMEQ}{\phantom{{}={}}}
\newcommand{\SQRT}[1]{\sqrt{#1}}
\newcommand{\PS}[1]{\left(#1\right)}
\newcommand{\SGN}{\textrm{sgn}}
\newcommand{\DOTNAME}[1]{\quad\cdots(#1)}
\newcommand{\BAR}[1]{\overline{#1}}
\newcommand{\TRIANGLE}{\triangle}
\newcommand{\TT}[1]{\textrm{#1}}
\newcommand{\TTred}[1]{\textcolor{red}{\textrm{#1}}}
\newcommand{\TTblue}[1]{\textcolor{blue}{\textrm{#1}}}
\newcommand{\ANGLE}[1]{\angle\textrm{#1}}
\newcommand{\TRI}[1]{\triangle\textrm{#1}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\PB}{\TT{PB}}
\newcommand{\BQ}{\TT{BQ}}
\newcommand{\QC}{\TT{QC}}
\newcommand{\CR}{\TT{CR}}
\newcommand{\RA}{\TT{RA}}
\newcommand{\AA}{\TT{AA}}
\newcommand{\AB}{\TT{AB}}
\newcommand{\AC}{\TT{AC}}
\newcommand{\CA}{\TT{CA}}
\newcommand{\AD}{\TT{AD}}
\newcommand{\AE}{\TT{AE}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\AQ}{\TT{AQ}}
\newcommand{\AR}{\TT{AR}}
\newcommand{\PQ}{\TT{PQ}}
\newcommand{\QR}{\TT{QR}}
\newcommand{\BC}{\TT{BC}}
\newcommand{\CA}{\TT{CA}}
\newcommand{\LONGVEC}[1]{\overrightarrow{#1}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vPB}{\LONGVEC{\PB}}
\newcommand{\vBQ}{\LONGVEC{\BQ}}
\newcommand{\vQC}{\LONGVEC{\QC}}
\newcommand{\vCR}{\LONGVEC{\CR}}
\newcommand{\vRA}{\LONGVEC{\RA}}
\newcommand{\vAA}{\LONGVEC{\AA}}
\newcommand{\vAB}{\LONGVEC{\AB}}
\newcommand{\vBC}{\LONGVEC{\BC}}
\newcommand{\vCA}{\LONGVEC{\CA}}
\newcommand{\vDE}{\LONGVEC{\DE}}
\newcommand{\vAD}{\LONGVEC{\AD}}
\newcommand{\vAE}{\LONGVEC{\AE}}
\newcommand{\vAC}{\LONGVEC{\AC}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vAQ}{\LONGVEC{\AQ}}
\newcommand{\vAR}{\LONGVEC{\AR}}
\newcommand{\vPQ}{\LONGVEC{\PQ}}
\newcommand{\vQR}{\LONGVEC{\QR}}
\newcommand{\avAP}{\ABS{\vAP}}
\newcommand{\avPB}{\ABS{\vPB}}
\newcommand{\avBQ}{\ABS{\vBQ}}
\newcommand{\avQC}{\ABS{\vQC}}
\newcommand{\avCR}{\ABS{\vCR}}
\newcommand{\avRA}{\ABS{\vRA}}
\newcommand{\va}{\vec{a}}
\newcommand{\vb}{\BLUEFOCUS{\vec{b}}}
\newcommand{\vc}{\REDFOCUS{\vec{c}}}
\newcommand{\vZ}{\vec{0}}
\newcommand{\CHOTEN}{\REDFOCUS{\textbf{頂点}}}
\newcommand{\KOUTEN}{\BLUEFOCUS{\textbf{交点}}}
\definecolor{MUTE-COLOR}{rgb}{0.6,0.6,0.6}%
\definecolor{NOMUTE-COLOR}{rgb}{0.0,0.0,0.0}%
\definecolor{REDNOMUTE-COLOR}{rgb}{1.0,0.0,0.0}%
\newcommand{\MUTE}[1]{\textcolor{MUTE-COLOR}{\TT{#1}}}
\newcommand{\NOMUTE}[1]{\textcolor{NOMUTE-COLOR}{\TT{#1}}}
\newcommand{\REDNOMUTE}[1]{\textcolor{REDNOMUTE-COLOR}{\TT{#1}}}
\newcommand{\mvAA}{\LONGVEC{\MUTE{A}\NOMUTE{A}}}
\newcommand{\mvAB}{\LONGVEC{\MUTE{A}\NOMUTE{B}}}
\newcommand{\mvAC}{\LONGVEC{\MUTE{A}\NOMUTE{C}}}
\newcommand{\mvAP}{\LONGVEC{\MUTE{A}\NOMUTE{P}}}
\newcommand{\mvAQ}{\LONGVEC{\MUTE{A}\NOMUTE{Q}}}
\newcommand{\mvAR}{\LONGVEC{\MUTE{A}\NOMUTE{R}}}
\newcommand{\mvAV}{\LONGVEC{\MUTE{A}\NOMUTE{V}}}
\newcommand{\mvRevAB}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{B}}}
\newcommand{\mvRevAC}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{C}}}
\newcommand{\mvAD}{\LONGVEC{\MUTE{A}\NOMUTE{D}}}
\newcommand{\mvAE}{\LONGVEC{\MUTE{A}\NOMUTE{E}}}
\newcommand{\mvAF}{\LONGVEC{\MUTE{A}\NOMUTE{F}}}
\newcommand{\BP}{\TT{BP}}
\newcommand{\vBP}{\LONGVEC{\BP}}
\newcommand{\NEAREQ}{\fallingdotseq}
\newcommand{\DE}{\TT{DE}}
\newcommand{\CD}{\TT{CD}}
\newcommand{\BE}{\TT{BE}}
\newcommand{\AF}{\TT{AF}}
\newcommand{\BF}{\TT{BF}}
\newcommand{\FB}{\TT{FB}}
\newcommand{\BE}{\TT{BE}}
\newcommand{\CF}{\TT{CF}}
\newcommand{\AG}{\TT{AG}}
\newcommand{\BG}{\TT{BG}}
\newcommand{\DB}{\TT{DB}}
\newcommand{\FE}{\TT{FE}}
\newcommand{\EC}{\TT{EC}}
\newcommand{\CG}{\TT{CG}}
\newcommand{\GB}{\TT{GB}}
\newcommand{\BA}{\TT{BA}}
\newcommand{\DF}{\TT{DF}}
\newcommand{\FC}{\TT{FC}}
\newcommand{\EA}{\TT{EA}}
\newcommand{\vAF}{\LONGVEC{\AF}}
\newcommand{\vBF}{\LONGVEC{\BF}}
\newcommand{\vBE}{\LONGVEC{\BE}}
\newcommand{\vCF}{\LONGVEC{\CF}}
\newcommand{\vCD}{\LONGVEC{\CD}}
\newcommand{\vAG}{\LONGVEC{\AG}}
\newcommand{\vBG}{\LONGVEC{\BG}}
$
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。
好奇心旺盛で根気強い《元気少女》。言葉が大好き。
図書室にて
ここは高校の図書室。いまは放課後。
僕は後輩のテトラちゃんといっしょに図形の問題をベクトルを使って考えていた。
証明が終わったところでテトラちゃんは何かを思いついたようだ。
問題
平面上に三角形 $\TT{ABC}$ がある。
辺 $\BC$ と平行な直線が、
直線 $\AB,\AC$ と交わる点をそれぞれ点 $\TT{D},\TT{E}$ とする。
線分 $\CD$ と線分 $\BE$ の交点を $\TT{F}$ とする。
直線 $\AF$ と辺 $\BC$ の交点を $\TT{G}$ とする。
このとき、点 $\TT{G}$ は辺 $\BC$ の中点であることを証明せよ。
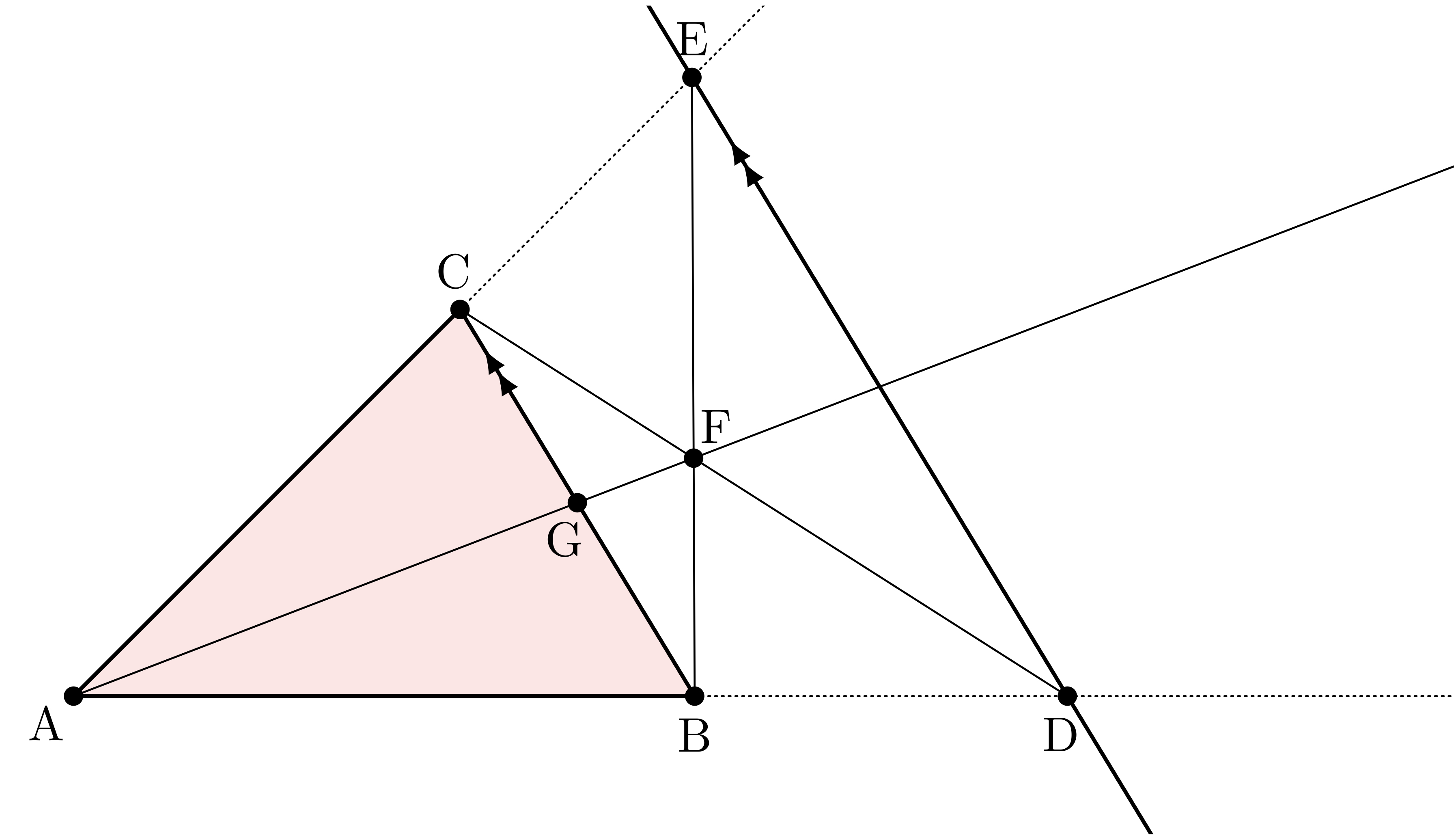
参考:モノグラフ『ベクトル』(科学新興社)
テトラ「でも、先輩。
これで証明はできました(第435回参照)が、
なかなか大変ですね……」
僕「そうだねえ、
一次独立な二つのベクトル $\vb$ と $\vc$ で表して、計算に持ち込むのはいいけれど、
大変なのは確かだ」
テトラ「先輩? いまの問題でふと思ったことがあるんですけど……」
僕「思ったこと?」
テトラ「はい。この図には、三角形の二辺と交わる直線があるのが見つかります。
いままでは $\TRI{ABC}$ に注目していましたが、 $\TRI{ABE}$ と直線 $\CD$ に注目するんです」
$\TRI{ABE}$ と直線 $\CD$ に注目する

僕「うん? ……ああ、なるほど。メネラウスの定理を使うつもり?」
テトラ「はいっ! その通りです」
僕「なるほどね。僕はメネラウスの定理を証明するときに、
《補助線を使う証明》をしたあとで《ベクトルを使う証明》に気付いたけど(第432回参照)、
テトラちゃんは反対のパターンをやろうと思ったんだ」
テトラ「ですです。確かにベクトルも面白いんですが、
この図を見ていると、いかにもメネラウスの定理が使えそうです。
つまり、 $\TRI{ABE}$ と直線 $\CD$ に対して、
- $\CHOTEN$ は $\TT{A},\TT{B},\TT{E}$
- $\KOUTEN$ は $\TT{D},\TT{F},\TT{C}$
になりますよね」
頂点と交点

僕「そうだね。あれ……でも……」
テトラ「大丈夫です。
$$
\CHOTEN \to \KOUTEN \to
\CHOTEN \to \KOUTEN \to
\CHOTEN \to \KOUTEN
$$
の順番でたどれば、
メネラウスの定理を間違えることはありません!」
$\TRI{ABE}$ と直線 $\CD$ にメネラウスの定理をあてはめる(図1)

$\TRI{ABE}$ と直線 $\CD$ についてメネラウスの定理より、

が成り立つ。
僕「テトラちゃん、テトラちゃん、これはまずくない?」
テトラ「先輩、先輩、どうしてでしょう? 間違ってませんよね?」
僕「うん、メネラウスの定理はまちがっていないし、
$\TRI{ABE}$ と直線 $\CD$ にあてはめるのもまちがっていない。
でも、それはいまの問題解決には役立たないような気がするんだけど」
テトラ「いまの問題解決には役立たないとは……あっ! 確かに」
僕「だよね」
メネラウスの定理を使って証明したい
問題(再掲)
平面上に三角形 $\TT{ABC}$ がある。
辺 $\BC$ と平行な直線が、
直線 $\AB,\AC$ と交わる点をそれぞれ点 $\TT{D},\TT{E}$ とする。
線分 $\CD$ と線分 $\BE$ の交点を $\TT{F}$ とする。
直線 $\AF$ と辺 $\BC$ の交点を $\TT{G}$ とする。
このとき、点 $\TT{G}$ は辺 $\BC$ の中点であることを証明せよ。

参考:モノグラフ『ベクトル』(科学新興社)
テトラ「いま確かめたいのは点 $\TT{G}$ が辺 $\BC$ の中点になるか?ということでした。
$\CG:\GB = 1:1$ になること、
つまり、
$$
\frac{\CG}{\GB} = 1
$$
を確かめるんですが、あたしのメネラウスの定理は点 $\TT{G}$ をスルーしちゃってましたっ!」
点 $\TT{G}$ をスルーしている

僕「うん、でもテトラちゃんのアイディアは素晴らしいよ。
僕はベクトルを使うことばかり考えていて、メネラウスの定理を使ってみようとは思わなかったから」
テトラ「$\CG:\GB = 1:1$ を調べたいのであれば、
点 $\TT{G}$ がうまく交点になるような三角形と直線を見つけ出す必要があるんですね」
僕「$\frac{\CG}{\GB}$
が出てくるように
メネラウスの定理を当てはめられる
三角形と直線——あ、すぐに見つかるね!」

三角形を見つけよう
テトラ「あたしも見つけました! $\TRI{CBD}$ と直線 $\AF$ を使えば、
うまく $\CG:\GB$ が出てきます」
$\TRI{CBD}$ と直線 $\AF$ に注目

$\TRI{CBD}$ と直線 $\AF$ にメネラウスの定理を当てはめる(図2)

$\TRI{CBD}$ と直線 $\AF$ についてメネラウスの定理より、
$$
\frac{\BA}{\AD}
\times
\frac{\DF}{\FC}
\times
\FOCUS{\frac{\CG}{\GB}}
=
1
$$
が成り立つ。
僕「そうだね」
テトラ「これで調べたい $\FOCUS{\frac{\CG}{\GB}}$ は出てきましたが……
$$
\frac{\BA}{\AD}
\quad\textrm{や}\quad
\frac{\DF}{\FC}
$$
はわからないままですね」
僕「……」
テトラ「だとしたら、ダメでしたか……」
僕「僕は見つけてしまった」
テトラ「え?」
異なる三角形を見つけよう
僕「図2の場合とは異なる三角形に、メネラウスの定理を当てはめられるよ。
しかもまた、
$\frac{\CG}{\GB}$
が出てくる三角形と直線がある」
テトラ「い、言わないでください。あたしも見つけたい!」
$\frac{\CG}{\GB}$ が出てくる三角形、見つかる?


僕「見つかった?」
![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」











