![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリはメネラウスの定理の証明に取り組んでいた。
僕たちは、それぞれ違う補助線を引いて証明ができたところ(第431回参照)。
メネラウスの定理
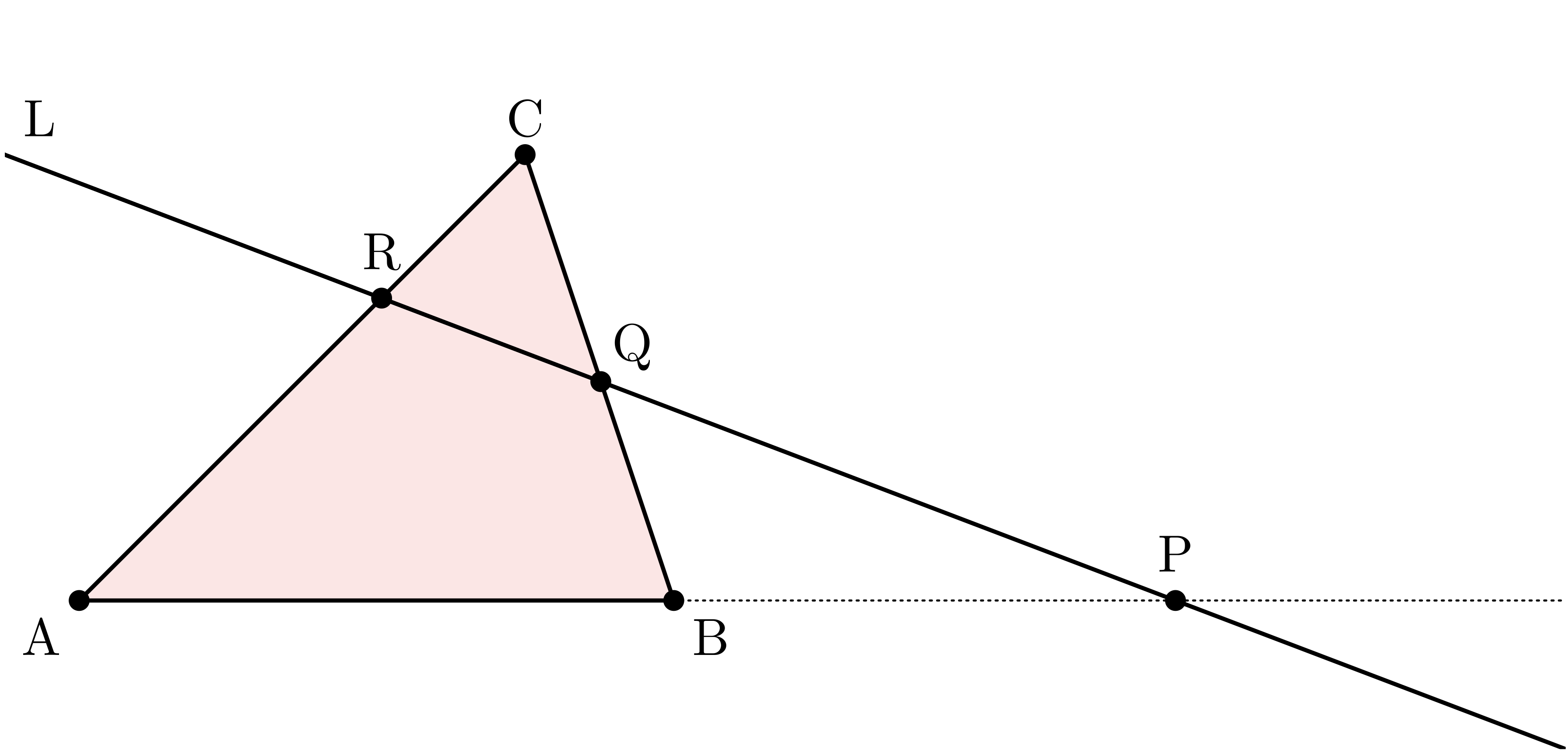
平面上に三角形 $\TT{ABC}$ がある。
また図のように、 辺 $\BC$ と辺 $\CA$ に交わる直線 $\TT{L}$ がある。
このとき、
$$ \frac{\AP}{\PB} \times \frac{\BQ}{\QC} \times \frac{\CR}{\RA} = 1 $$
が成り立つ。
僕「ユーリはなかなかうまい補助線を引いたよね(第431回参照)」
ユーリ「うまく見つけられれば、うまい補助線になるもん!」
そこで僕は、あることに気付いた。
僕「ねえユーリ。気付いたことがある」
ユーリ「なになに? もっとうまい補助線? もっと簡単になる?」
僕「いや、たぶん簡単にはならない」
ユーリ「だったら意味ないじゃん!」
僕「簡単じゃない。でも、 補助線がたとえ見つけられなくても構わない。 補助線を使わなくても、メネラウスの定理は証明できる……と思う」
ユーリ「『と思う』なんだ」
僕「最後まで見通しているわけじゃないからだよ。 どうすればいいかというと、ベクトルを使う」
ユーリ「べくとる」
僕「ユーリはベクトルを知ってるよね。このあいだ教えたし」
【CM】
テトラ「はいっ、ここでお知らせがあります。 先輩とユーリちゃんの活躍は 『数学ガールの秘密ノート/ベクトルの真実』をお読みくださいね!」
テトラ「ベクトルの真実ですよ! ベクトル真実ちゃんじゃありませんからね……」
ユーリ「テトラさん、定番ギャグを飛ばしてる」
僕「メタ発言自重」
ユーリ「何の話だっけ」
僕「ともかく、ベクトルを使ってメネラウスの定理を証明できると思った——という話」
ユーリ「ふーん。じゃ、やってみて」
僕「ただ、ちょっと問題がある。 たぶん、ややこしい計算が出てくると思うから、かなり《腕力》がいるかな」
ユーリ「数学やるのに腕力がいるの?」
僕「《腕力》というのはたとえだよ。 長くてややこしい計算をまちがえなくこなす必要があるってこと」
ユーリ「何でわざわざそんな方法を選ぶの? 補助線引いて証明できたのに」
僕「補助線を引いて証明するには《ひらめき》がいる。 でもメネラウスの定理をベクトルで証明するには《腕力》があればたぶん行けると思う。 《ひらめき》が要らない……とまでいえるかどうかはわからないけど」
ユーリ「《腕力》とか《ひらめき》とか意味不明すぎ」
僕「補助線を引く《ひらめき》というのは、その問題固有の方法になるよね。 つまり、その問題だけの方法。同じ方法を他の問題には使えない」
ユーリ「平行線を引くとか、二等分線を引くとか、そんなもんだけどね」
僕「メネラウスの定理をベクトルで証明する方法は、 《連立方程式を立てる》みたいに、いろんな問題に使える方法になる……と思う」
ユーリ「まだ証明してないのに、何でそんなこと言えんの?」
僕「ベクトルを使って図形問題を解いたり証明したりするのは、 何回かやったことがあるからだよ。 うまくベクトルを使うと、うまく解けるんだ」
ユーリ「また出た。 うまく使えばうまく解けるなんて、あたりまえじゃん。 うまく解けるのがうまい使い方なのじゃよ。 ごちゃごちゃ言ってないで、証明してみせたまえ!」
僕「よーし、やってみるか!」
こんなふうにして、 僕はもう一度、メネラウスの定理を証明することになった。
今度は、ベクトルを使うのだ。
ユーリ「そもそもさー、ベクトルを使うってどーゆーこと? ベクトルって矢印でしょ?」
僕「そうだね。いまからメネラウスの定理を証明するけど、 そこでは頂点や交点や直線がたくさん出てくる」
ユーリ「三角形とか」
僕「そういうこと。そこで基本になるのはやっぱり点だよね。 しかも点と点の位置関係が大事になる。 ベクトルを使って考えるというのは、その《点と点の位置関係》をベクトルで表すこと——まずは」
ユーリ「それって、こーゆーこと?」
メネラウスの定理の図に矢印を入れ込む
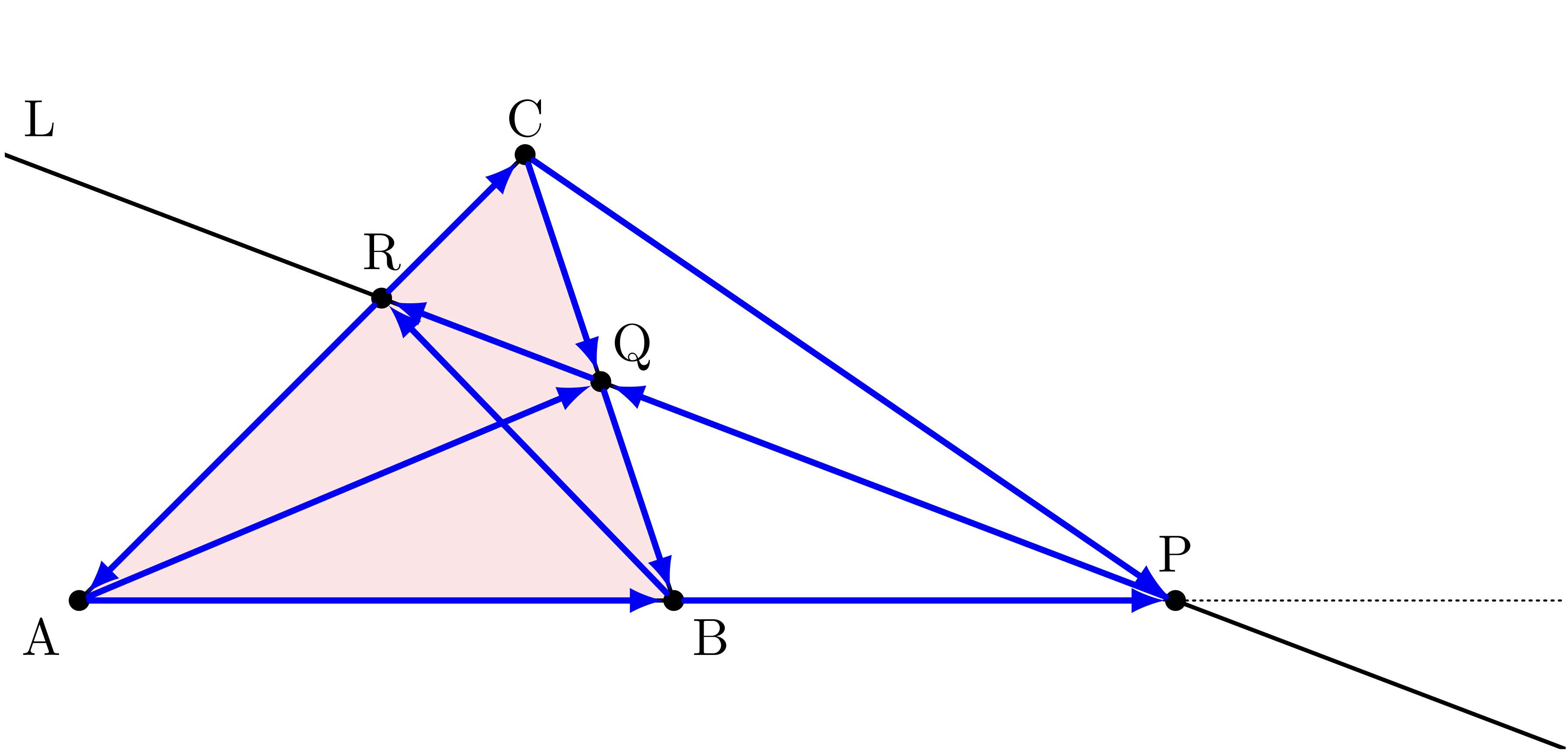
僕「まさに、そういうこと」
ユーリ「うーん……でも、単にごちゃごちゃするだけでは?」
僕「それは図に矢印を一気にたくさん描いたからだよ。 一気に進むと混乱するし、 僕もまだ、うまくいくかどうかわかっていない。 考えながら、少しずつ証明していこう」
ユーリ「ユーリさあ……ベクトルのこと、あんまり覚えてないかも」
僕「わからないところがあったら説明するよ。 まずはメネラウスの定理をもう一度確認しよう」
メネラウスの定理(再掲)
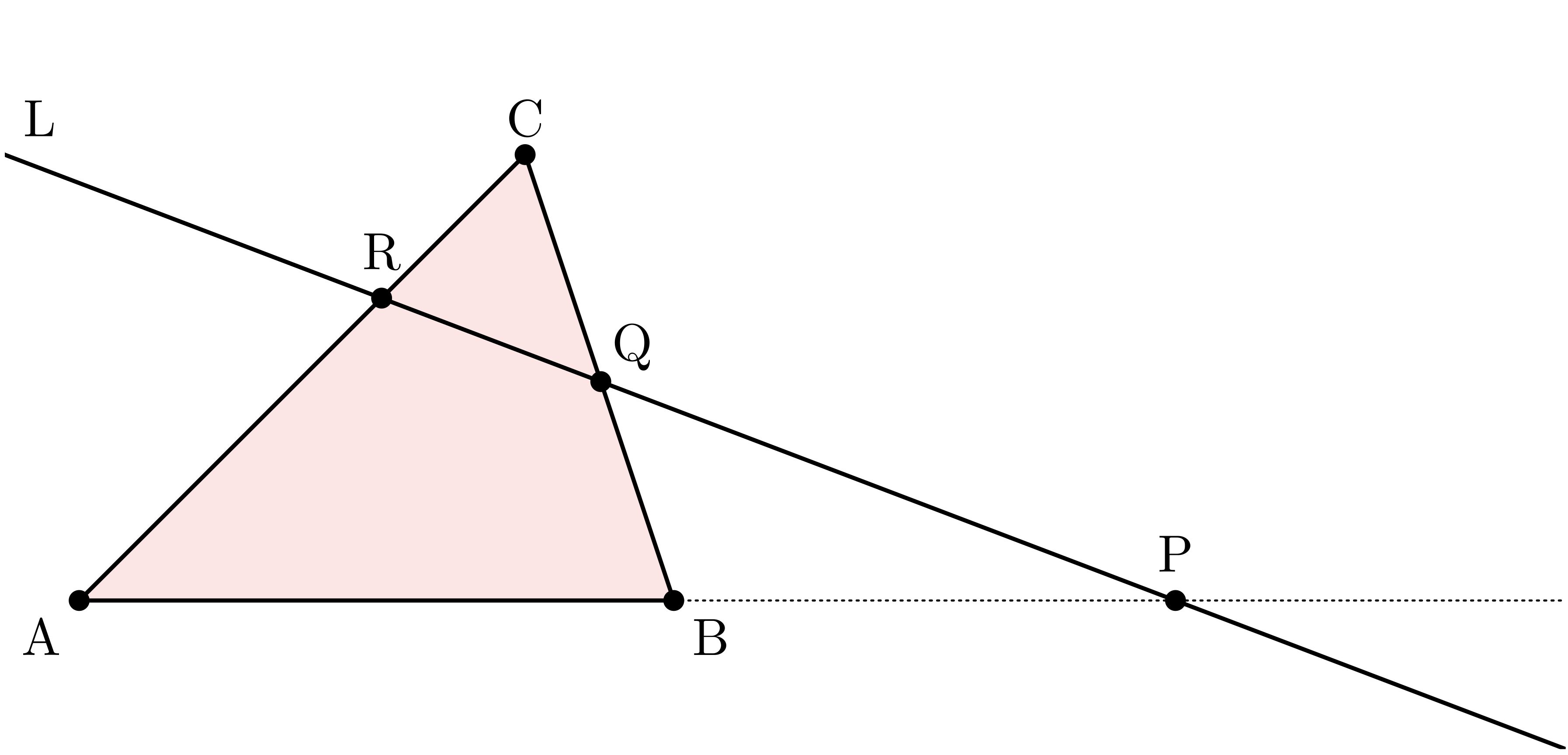
平面上に三角形 $\TT{ABC}$ がある。
また図のように、 辺 $\BC$ と辺 $\CA$ に交わる直線 $\TT{L}$ がある。
このとき、
$$ \frac{\AP}{\PB} \times \frac{\BQ}{\QC} \times \frac{\CR}{\RA} = 1 $$
が成り立つ。
ユーリ「そんで、《ベクトルで考える》とどーなんの?」
僕「まずは証明したい式を見る。ここに出てくる $$ \frac{\AP}{\PB} \times \frac{\BQ}{\QC} \times \frac{\CR}{\RA} $$ というのは《線分の長さの比》を使って計算しているよね」
ユーリ「そだね。 $\AP$ の長さ割る $\PB$ の長さとか……掛け算すると $1$ になる」
僕「たとえば、 $$ \frac\AP\PB $$ に注目する」
ユーリ「ふむふむ?」
僕「$\frac\AP\PB$ に出てくる $\TT{A},\TT{P},\TT{B}$ は一本の直線上にある異なる三点だよね。 そのことはベクトルを使って、 $$ \vAP = p\vPB $$ という実数 $p$ が存在すると言い換えられる」
ユーリ「なんで?」
僕「$\vAP$ と $\vPB$ という二つのベクトルを図に描いてみると、 こんな風になる。
二つのベクトル $\vAP$ と $\vPB$
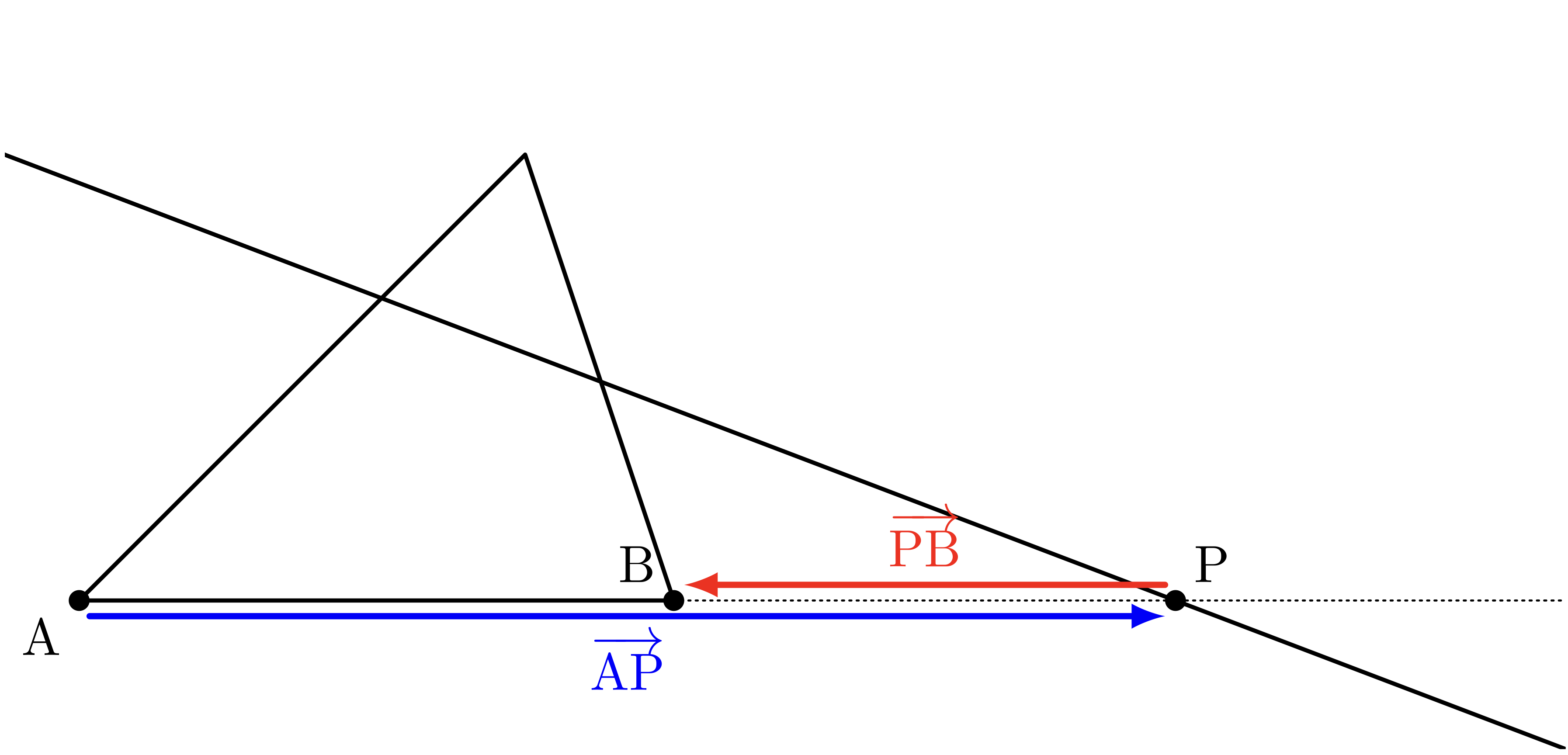
僕「つまり、 $\vAP$ と $\vPB$ のベクトルの方向は同じだけど、 大きさは同じかどうかわからない。 でも $\vPB$ を $p$ 倍してやれば $\vAP$ と等しくなるような実数 $p$ がある」
ユーリ「$\vAP$ と $\vPB$ って反対向きじゃん」
僕「《向き》は反対だけど《方向》は同じだよ。でもその指摘はとても重要。さすがユーリだ。 向きが逆というのは、さっきの実数 $p$ が $p < 0$ であることに対応しているから」
ユーリ「$\vAP = p\vPB$ で $p$ がマイナスだと反対向きのベクトル……あ、何だか思い出してきた。 数をベクトルに掛けると伸び縮みするんじゃなかったっけ?」
僕「その通り。 ベクトルのスカラー倍だね。 たとえば、 $\vAB$ を同じ向きで $2$ 倍の大きさにしたベクトルは $2\vAB$ と表す。 $\vAB$ 自身は $1\vAB$ ということ。そして同じ大きさで反対向きだったら $-1\vAB$ で、 これは普通は $-\vAB$ と表す」
$\vAB$ のスカラー倍
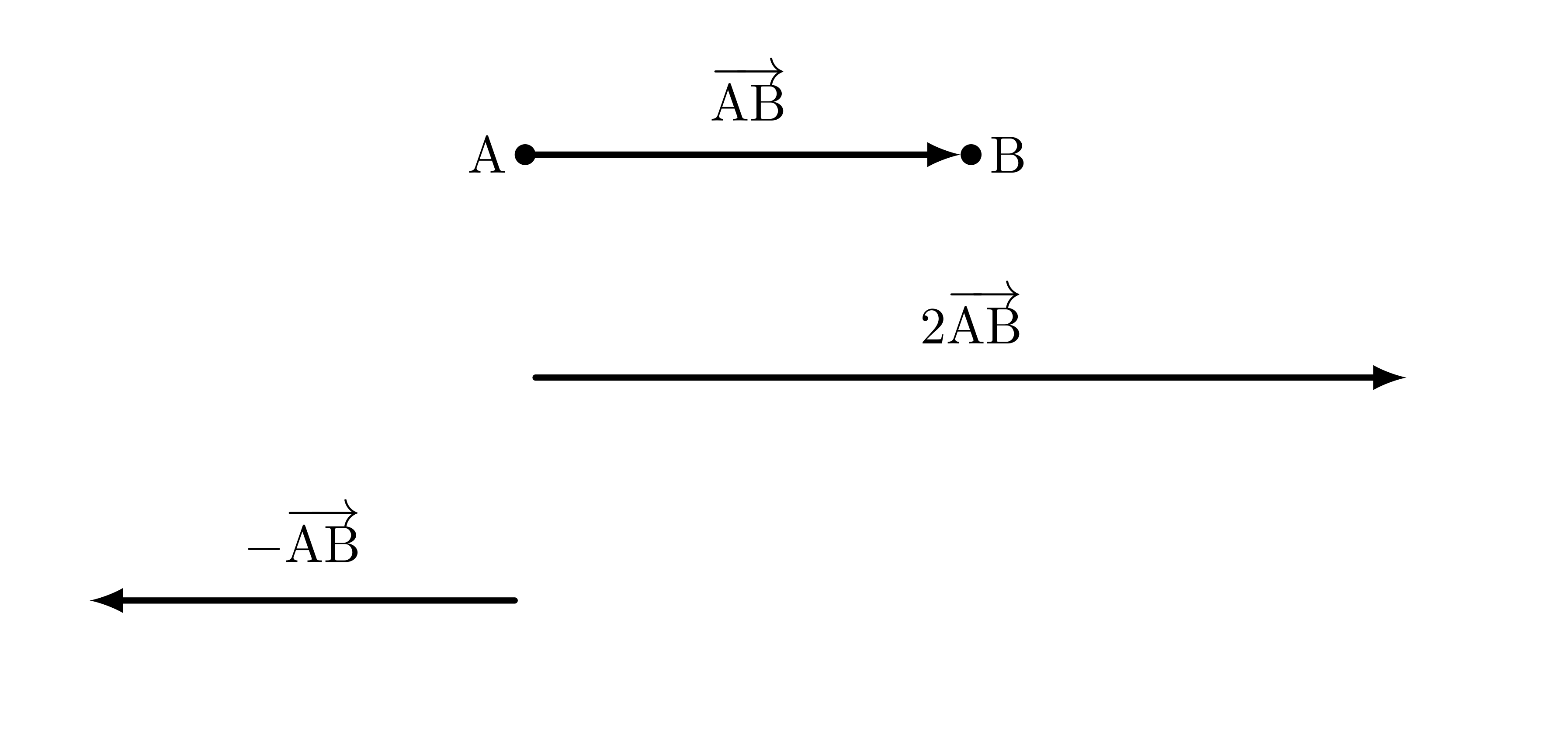
僕「そしてベクトルのスカラー倍を使うと、 $\TT{A},\TT{P},\TT{B}$ という異なる $3$ 点が《直線上にある》ということは、 $$ \vAP = p\vPB $$ という実数 $p$ が存在すると表現できる——これは、 $\TT{A},\TT{P},\TT{B}$ の位置関係をベクトルを使って表したことになる」
ユーリ「ちょっとわかった。それが《ベクトルで考える》ってことだ!」
僕「そうだね」
ユーリ「でも、めんどくさ! なんでそんなことすんの?」
僕「計算に持ち込むためだよ。図形的に $3$ 個の点を考えるのではなく、 $\vAP = p\vPB$ を満たす実数 $p$ という数に置き換えて考える。あとで、この $p$ を計算しようという心づもりがある」
ユーリ「図形を計算するってこと? ヤバくない?」
僕「別にヤバくはないよ。ところで話を戻すと 僕たちは、 $$ \frac\AP\PB $$ を考えたいんだった。この分数の値は、
《$\PB$ の長さ》を何倍したら《$\AP$ の長さ》になるか
を意味しているよね」
ユーリ「えーと? たとえばもしも $\PB = 3$ で $\AP = 6$ だったら、 $$ \frac\AP\PB = \frac{6}{3} = 2 $$ だから、《$\PB$ の長さ》を $2$ 倍したら《$\AP$ の長さ》になる。了解、了解」
僕「具体的に考えてみたのは偉いな」
ユーリ「こんなのは基本ですゼ。分子と分母をうっかりまちがえないよーに」
僕「だから《$\PB$ の長さ》を $\frac\AP\PB$ 倍したら《$\AP$ の長さ》になる」
ユーリ「むむむ? それって $p$ じゃないの? だって $\vAP = p\vPB$ なんだから」
僕「そうかな? $p < 0$ だよ?」
ユーリ「あっ、違った。絶対値だ! だから、 $$ \frac\AP\PB = \ABS{p} $$ になる!」
僕「その通り。 $\AP = \avAP$ で $\PB = \avPB$ と表すと、 $$ \frac\AP\PB = \frac\avAP\avPB = \ABS{p} $$ ということになる」
ユーリ「ごちゃごちゃしてきた」
僕「表記がいろいろでてきたからね。いったんここまでを整理しようか」
異なる $3$ 点 $\TT{A},\TT{P},\TT{B}$ が一つの直線上にあることは、 $$ \vAP = p\vPB $$ という実数 $p$ が存在することである。
ベクトルの大きさ(長さ)
ベクトル $\vAP$ の大きさを $\avAP$ と表す。これは点 $\TT{A}$ と $\TT{P}$ の距離に等しい。 すなわち、線分 $\AP$ の長さに等しい。 $$ \AP = \avAP $$
ユーリ「だいぶ思い出してきた。要するに矢印じゃんね」
僕「じゃあ、またメネラウスの定理に戻るよ。いま僕たちは、 三点 $\TT{A},\TT{P},\TT{B}$ が一直線上にあることから、 $$ \vAP = p\vPB $$ という式を満たす実数に $p$ という名前をつけたところ。 どうしてそんな数を考えるかというと、 $$ \REDFOCUS{\frac\AP\PB} = \ABS{p} $$ が成り立つから。 つまり、証明したい式に出てくる、 $\frac{\AP}{\PB}$ のところを攻略したわけだ。 $\ABS{p}$ になる」
$$ \underbrace{\REDFOCUS{\frac{\AP}{\PB}}}_{=\ABS{p}} \times \frac{\BQ}{\QC} \times \frac{\CR}{\RA} $$ユーリ「わかった! ズバリ、残り二つの分数にも同じことをするでしょー!」
僕「その通り!」
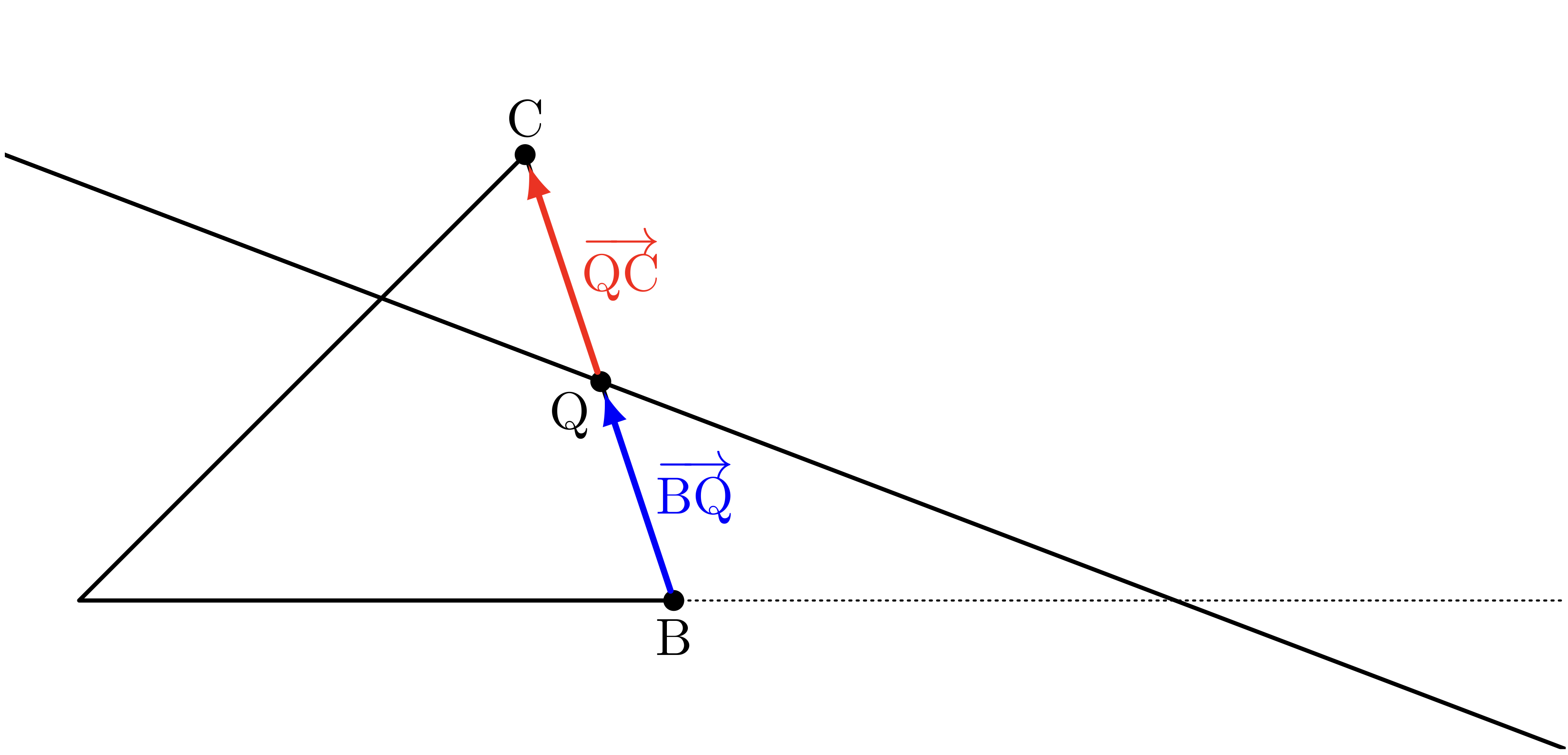
僕「$\frac\BQ\QC$ に出てくる $\TT{B},\TT{Q},\TT{C}$ は一直線上にある。 だから今度は実数 $q$ を使って、 $$ \vBQ = q\vQC $$ と表せる。 これで $\frac{\BQ}{\QC}$ は $\ABS{q}$ ということになるね。 さっきと同じ考え方だ」
$$ \underbrace{\frac{\AP}{\PB}}_{=\ABS{p}} \times \underbrace{\REDFOCUS{\frac{\BQ}{\QC}}}_{=\ABS{q}} \times \frac{\CR}{\RA} $$ユーリ「ふーん……ねえお兄ちゃん。 今度は $q > 0$ だよね。だって、 $\vBQ$ と $\vQC$ は同じ向きだから」
僕「その通り!」
ユーリ「だったら、 $\ABS{q}$ じゃなくて、 $q$ でも同じだよね?」
僕「うん、そうだよ。でもいまは点の位置関係を気にしたくないから $\ABS{q}$ のままにしておく。いい?」
ユーリ「まーよかろー」
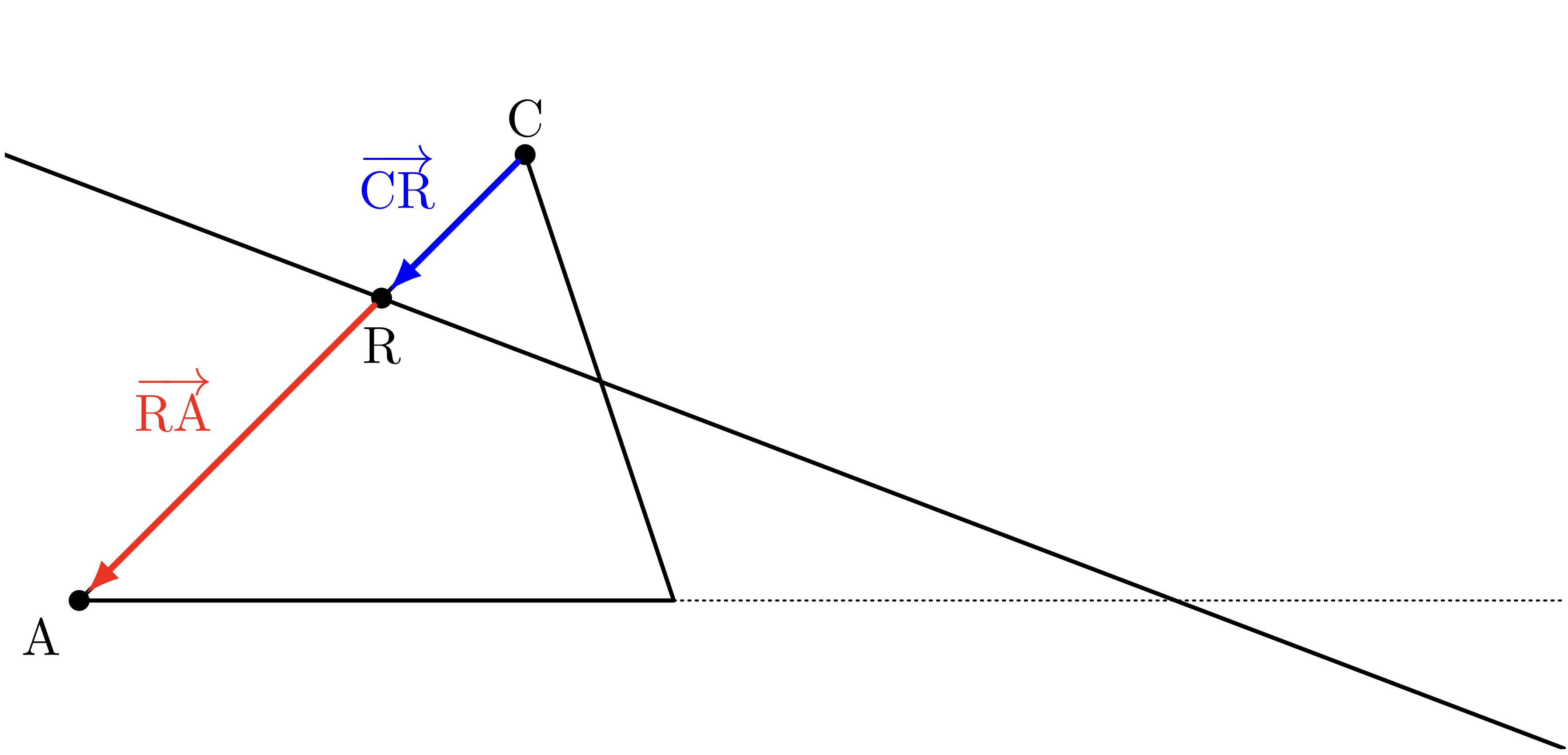
僕「$\frac\CR\RA$ に出てくる $\TT{C},\TT{R},\TT{A}$ は一直線上にある。 これまでと同様に考えて——」
ユーリ「実数 $r$ を使って、 $$ \vCR = r\vRA $$ でしょ? 同じこと三回繰り返してる」
$$ \underbrace{\frac{\AP}{\PB}}_{=\ABS{p}} \times \underbrace{\frac{\BQ}{\QC}}_{=\ABS{q}} \times \underbrace{\REDFOCUS{\frac{\CR}{\RA}}}_{=\ABS{r}} $$僕「そうだね。同じことを繰り返している。 さて、ここからどうするのか……」
ユーリ「計算して $1$ になればいいんじゃないの?」
僕「いや、まだそれは無理だよ。 $p,q,r$ という三つの実数が出てきただけで、 まだ何も計算はできないから」
ユーリ「やっぱり《ひらめき》がいるんじゃないの?」
僕「おかしいな……ああ、わかった。《与えられた条件をすべて使ったか》という問いかけを忘れていた。 まだ使ってない条件があった」
ユーリ「メネラウスの定理で?」
僕「そうだよ。わかる?」
ユーリ「えーっと……使ってない条件とな?」
メネラウスの定理(再再掲)

平面上に三角形 $\TT{ABC}$ がある。
また図のように、 辺 $\BC$ と辺 $\CA$ に交わる直線 $\TT{L}$ がある。
このとき、
$$ \frac{\AP}{\PB} \times \frac{\BQ}{\QC} \times \frac{\CR}{\RA} = 1 $$
が成り立つ。

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年9月20日)