$
\newcommand{\TEXT}[1]{\textbf{#1}}
\newcommand{\REMTEXT}[1]{\textbf{#1}}
\definecolor{CUD-GREEN}{rgb}{0.012,0.686,0.478}% 3,175,122
\newcommand{\MARK}[1]{\textcolor{red}{#1}}
\newcommand{\MARKA}[1]{\textcolor{red}{#1}}
\newcommand{\MARKB}[1]{\textcolor{blue}{#1}}
\newcommand{\MARKC}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\GEQ}{\geqq}
\newcommand{\LEQ}{\leqq}
\newcommand{\NEQ}{\neq}
\newcommand{\FOCUS}[1]{\fbox{ $#1$ }}
\newcommand{\REDFOCUS}[1]{\textcolor{red}{#1}}
\newcommand{\GREENFOCUS}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUEFOCUS}[1]{\textcolor{blue}{#1}}
\newcommand{\BROWNFOCUS}[1]{\textcolor{brown}{#1}}
\newcommand{\REDHEART}{\REDFOCUS{\heartsuit}}
\newcommand{\REDTEXT}[1]{\textcolor{red}{#1}}
\newcommand{\GREENTEXT}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUETEXT}[1]{\textcolor{blue}{#1}}
\newcommand{\ABS}[1]{|#1|}
\newcommand{\PHANTOMEQ}{\phantom{{}={}}}
\newcommand{\SQRT}[1]{\sqrt{#1}}
\newcommand{\PS}[1]{\left(#1\right)}
\newcommand{\SGN}{\textrm{sgn}}
\newcommand{\DOTNAME}[1]{\quad\cdots(#1)}
\newcommand{\BAR}[1]{\overline{#1}}
\newcommand{\TRIANGLE}{\triangle}
\newcommand{\TT}[1]{\textrm{#1}}
\newcommand{\TTred}[1]{\textcolor{red}{\textrm{#1}}}
\newcommand{\TTblue}[1]{\textcolor{blue}{\textrm{#1}}}
\newcommand{\ANGLE}[1]{\angle\textrm{#1}}
\newcommand{\TRI}[1]{\triangle\textrm{#1}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\PB}{\TT{PB}}
\newcommand{\BQ}{\TT{BQ}}
\newcommand{\QC}{\TT{QC}}
\newcommand{\CR}{\TT{CR}}
\newcommand{\RA}{\TT{RA}}
\newcommand{\AA}{\TT{AA}}
\newcommand{\AB}{\TT{AB}}
\newcommand{\BA}{\TT{BA}}
\newcommand{\AC}{\TT{AC}}
\newcommand{\CA}{\TT{CA}}
\newcommand{\AD}{\TT{AD}}
\newcommand{\AE}{\TT{AE}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\AQ}{\TT{AQ}}
\newcommand{\AR}{\TT{AR}}
\newcommand{\PQ}{\TT{PQ}}
\newcommand{\QR}{\TT{QR}}
\newcommand{\BC}{\TT{BC}}
\newcommand{\CB}{\TT{CB}}
\newcommand{\DA}{\TT{DA}}
\newcommand{\CA}{\TT{CA}}
\newcommand{\LONGVEC}[1]{\overrightarrow{#1}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vPB}{\LONGVEC{\PB}}
\newcommand{\vBQ}{\LONGVEC{\BQ}}
\newcommand{\vQC}{\LONGVEC{\QC}}
\newcommand{\vCR}{\LONGVEC{\CR}}
\newcommand{\vRA}{\LONGVEC{\RA}}
\newcommand{\vAA}{\LONGVEC{\AA}}
\newcommand{\vAB}{\LONGVEC{\AB}}
\newcommand{\vBA}{\LONGVEC{\BA}}
\newcommand{\vBC}{\LONGVEC{\BC}}
\newcommand{\vCB}{\LONGVEC{\CB}}
\newcommand{\vDA}{\LONGVEC{\DA}}
\newcommand{\vCA}{\LONGVEC{\CA}}
\newcommand{\vDE}{\LONGVEC{\DE}}
\newcommand{\vAD}{\LONGVEC{\AD}}
\newcommand{\vAE}{\LONGVEC{\AE}}
\newcommand{\vAC}{\LONGVEC{\AC}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vAQ}{\LONGVEC{\AQ}}
\newcommand{\vAR}{\LONGVEC{\AR}}
\newcommand{\vPQ}{\LONGVEC{\PQ}}
\newcommand{\vQR}{\LONGVEC{\QR}}
\newcommand{\avAP}{\ABS{\vAP}}
\newcommand{\avPB}{\ABS{\vPB}}
\newcommand{\avBQ}{\ABS{\vBQ}}
\newcommand{\avQC}{\ABS{\vQC}}
\newcommand{\avCR}{\ABS{\vCR}}
\newcommand{\avRA}{\ABS{\vRA}}
\newcommand{\va}{\vec{a}}
\newcommand{\vb}{\BLUEFOCUS{\vec{b}}}
\newcommand{\vc}{\REDFOCUS{\vec{c}}}
\newcommand{\vZ}{\vec{0}}
\newcommand{\CHOTEN}{\REDFOCUS{\textbf{頂点}}}
\newcommand{\KOUTEN}{\BLUEFOCUS{\textbf{交点}}}
\definecolor{MUTE-COLOR}{rgb}{0.6,0.6,0.6}%
\definecolor{NOMUTE-COLOR}{rgb}{0.0,0.0,0.0}%
\definecolor{REDNOMUTE-COLOR}{rgb}{1.0,0.0,0.0}%
\newcommand{\MUTE}[1]{\textcolor{MUTE-COLOR}{\TT{#1}}}
\newcommand{\NOMUTE}[1]{\textcolor{NOMUTE-COLOR}{\TT{#1}}}
\newcommand{\REDNOMUTE}[1]{\textcolor{REDNOMUTE-COLOR}{\TT{#1}}}
\newcommand{\mvAA}{\LONGVEC{\MUTE{A}\NOMUTE{A}}}
\newcommand{\mvAB}{\LONGVEC{\MUTE{A}\NOMUTE{B}}}
\newcommand{\mvAC}{\LONGVEC{\MUTE{A}\NOMUTE{C}}}
\newcommand{\mvAP}{\LONGVEC{\MUTE{A}\NOMUTE{P}}}
\newcommand{\mvAQ}{\LONGVEC{\MUTE{A}\NOMUTE{Q}}}
\newcommand{\mvAR}{\LONGVEC{\MUTE{A}\NOMUTE{R}}}
\newcommand{\mvAV}{\LONGVEC{\MUTE{A}\NOMUTE{V}}}
\newcommand{\mvOA}{\LONGVEC{\MUTE{O}\NOMUTE{A}}}
\newcommand{\mvOB}{\LONGVEC{\MUTE{O}\NOMUTE{B}}}
\newcommand{\mvOC}{\LONGVEC{\MUTE{O}\NOMUTE{C}}}
\newcommand{\mvOD}{\LONGVEC{\MUTE{O}\NOMUTE{D}}}
\newcommand{\mvRevAB}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{B}}}
\newcommand{\mvRevAC}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{C}}}
\newcommand{\mvAD}{\LONGVEC{\MUTE{A}\NOMUTE{D}}}
\newcommand{\mvAE}{\LONGVEC{\MUTE{A}\NOMUTE{E}}}
\newcommand{\mvAF}{\LONGVEC{\MUTE{A}\NOMUTE{F}}}
\newcommand{\BP}{\TT{BP}}
\newcommand{\vBP}{\LONGVEC{\BP}}
\newcommand{\NEAREQ}{\fallingdotseq}
\newcommand{\DE}{\TT{DE}}
\newcommand{\CD}{\TT{CD}}
\newcommand{\BE}{\TT{BE}}
\newcommand{\AF}{\TT{AF}}
\newcommand{\BF}{\TT{BF}}
\newcommand{\FB}{\TT{FB}}
\newcommand{\BE}{\TT{BE}}
\newcommand{\CF}{\TT{CF}}
\newcommand{\AG}{\TT{AG}}
\newcommand{\BG}{\TT{BG}}
\newcommand{\DB}{\TT{DB}}
\newcommand{\FE}{\TT{FE}}
\newcommand{\EC}{\TT{EC}}
\newcommand{\CG}{\TT{CG}}
\newcommand{\GB}{\TT{GB}}
\newcommand{\BA}{\TT{BA}}
\newcommand{\DF}{\TT{DF}}
\newcommand{\FC}{\TT{FC}}
\newcommand{\EA}{\TT{EA}}
\newcommand{\vAF}{\LONGVEC{\AF}}
\newcommand{\vBF}{\LONGVEC{\BF}}
\newcommand{\vBE}{\LONGVEC{\BE}}
\newcommand{\vCF}{\LONGVEC{\CF}}
\newcommand{\vCD}{\LONGVEC{\CD}}
\newcommand{\vAG}{\LONGVEC{\AG}}
\newcommand{\vBG}{\LONGVEC{\BG}}
\newcommand{\VECA}{\LONGVEC{\TT{A}}}
\newcommand{\VECB}{\LONGVEC{\TT{B}}}
\newcommand{\VECC}{\LONGVEC{\TT{C}}}
\newcommand{\VECD}{\LONGVEC{\TT{D}}}
$
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。
好奇心旺盛で根気強い《元気少女》。言葉が大好き。
図書室にて
ここは高校の図書室。いまは放課後。
僕は後輩のテトラちゃんといっしょに図形の問題をベクトルを使って考えていた(第436回参照)。
ひとしきり笑った後、テトラちゃんは真面目な顔になる。
テトラ「ところで先輩。そもそもの質問で申し訳ないんですが——」
僕「テトラちゃんの質問は『そもそも』が似合うよね」
テトラ「はい?」
僕「テトラちゃんの質問は、根源的なものが多いから」
テトラ「す、すみません。いつも話を振り出しに戻すみたいな質問ばかりで……」
僕「いやいや、とんでもない。
僕はテトラちゃんの質問から学んでいるような気がするんだ。
で、質問って?」
テトラ「あのですね、やっぱりあたしは『どうしてベクトルというものを考えるのか』が気になっています。
先輩のお話で、ベクトルを使うと図形の問題も計算に持ち込めるというお話はありましたけれど(第435回参照)」
僕「うん。
もちろん問題によるけど、
図形的な問題を解く手がかりを得られる点はあると思う。
補助線を発見できないときでも、とっかかりを見つけられるみたいに」
テトラ「確かにそうなんですけど、
でも計算で《腕力》が必要になったりします。
また、どのベクトルに注目するかにもよるので、
結局は何かを見つける必要はありそうに感じました」
僕「うんうん。それは僕もそう思う。だからベクトルを考えればすべてが解決するみたいな万能薬じゃないのは確か。
新しい視点で考えられるというのはあるかもしれないけど……」
テトラ「わかります。ベクトルで考えているときは、別の頭を使っているような気がします」
僕「そういえば、ベクトルを使う問題で、簡単だけどおもしろいものを思い出したよ。
ベクトルを使って考える意味が少しわかるかも」
テトラ「ベクトルを使って考える意味! それは何ですか?」
僕「それを説明する前に、簡単な問題を解いてみない?」
テトラ「もちろんですっ!」
僕「こういう問題だよ」
問題に挑戦
問題1
四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ に対して、
$$
\vAB + \vCD = \vAD + \vCB
$$
が成り立つことを証明せよ。

テトラ「問題文が短いので、私でも解けそうです」
僕「いやいや、問題文の長さで問題の難しさを判定するのは危険だと思うよ。
あ、ごめんごめん。考えの邪魔しちゃいけないね」
テトラ「はい、大丈夫です。
まずは、図形問題のセオリー通りに進むことにします。
ポリア先生の《図をかけ》ですね。ええと——四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ に対して、
この問題に出てくるベクトル、
$$
\vAB, \vCD, \vAD, \vCB
$$
をまずは描いてみます」
テトラちゃんの図
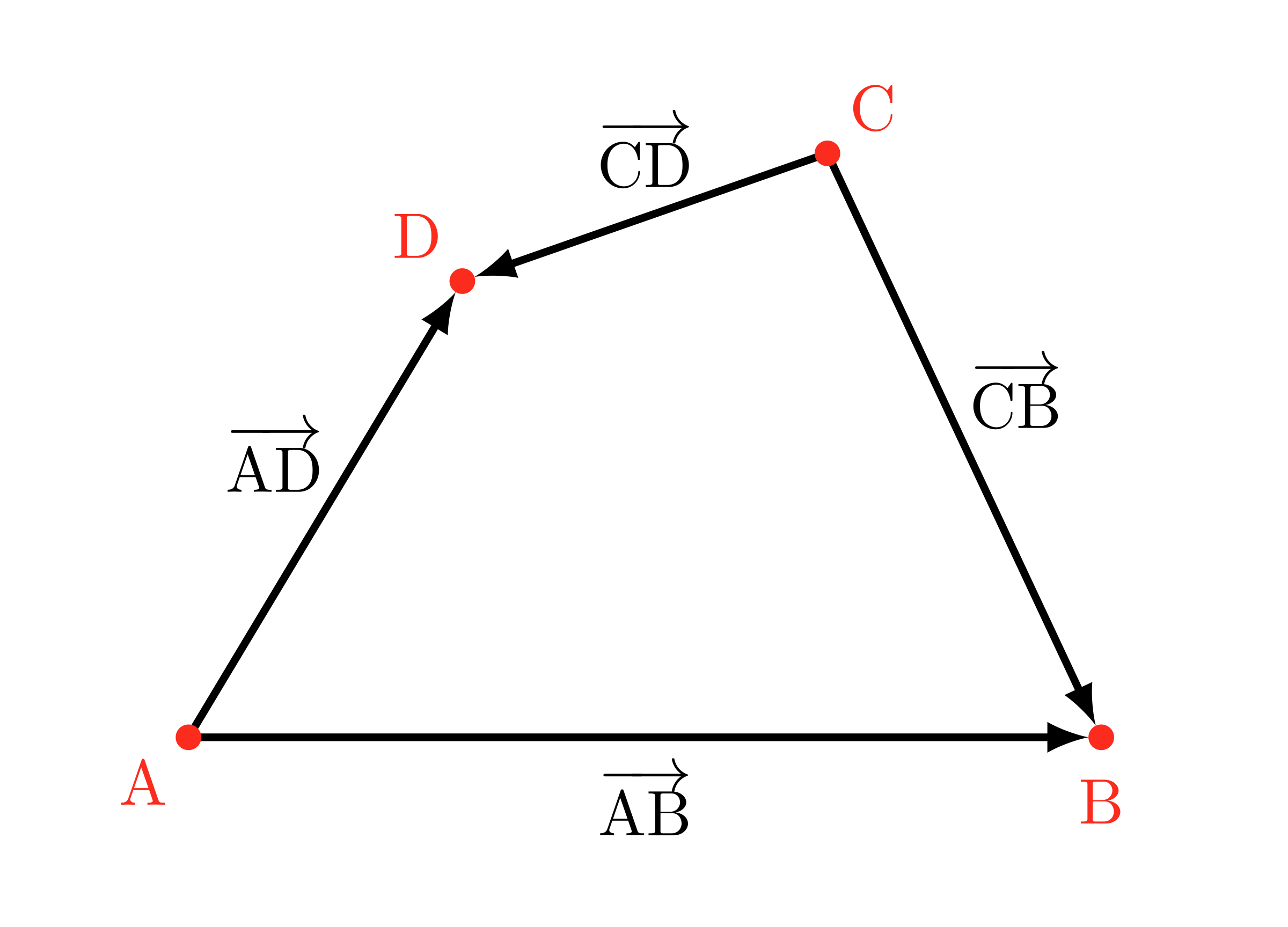
僕「……」
テトラ「はい、矢印で台形ができました。
あっ、じゃないじゃない。
台形とは限りません。台形は向かい合うひと組の辺が平行じゃなくちゃいけません。
これは、ただの四角形です」
僕「うん、そう。問題文には、四点に対する条件がまったくついてないから」
テトラ「それで《求めるものは何か》といえば、
$$
\vAB + \vCD = \vAD + \vCB
$$
という等式が成り立つということを示したい……はい、では、
すべてのベクトルを一つの点を基準にする方向で考えてみます」
僕「おお、学んだことをさっそく応用!」
一つの点を基準にする
テトラ「点 $\TT{A}$ を基準にして、
四つのベクトル $\vAB, \vCD, \vAD, \vCB$ をすべて書き換えますと……
$$
\begin{cases}
\vAB &= \mvAB \\
\vCD &= \mvAD - \mvAC \\
\vAD &= \mvAD \\
\vCB &= \mvAB - \mvAC \\
\end{cases}
$$
……となります。ということは、
$$
\begin{cases}
\vAB + \vCD &= \mvAB + \underbrace{\mvAD - \mvAC}_{\vCD}
= \mvAB - \mvAC + \mvAD \\
\vAD + \vCB &= \mvAD + \underbrace{\mvAB - \mvAC}_{\vCB}
= \mvAB - \mvAC + \mvAD
\end{cases}
$$
ということですから、確かに、
$$
\vAB + \vCD = \vAD + \vCB
$$
がいえました! これでいいですよね」
僕「《一つの点を基準にする》というベクトルの考え方を試して、見事に解決。お見事!
いまは $\TT{A}$ を基準にした《位置ベクトル》を考えたことになるけど、
もちろん $\TT{A},\TT{B},\TT{C},\TT{D}$ のどれを基準にしてもいい。
それからまったく関係がない新しい点 $\TT{O}$ をどこかに置いて、
それを基準にしても同じ結果になるよ」
新しい点を基準にする
テトラ「あ、そうなんですか!
勝手な点 $\TT{O}$ を使ってもうまくいくっておもしろいですね。
こういうことですか」
勝手な点 $\TT{O}$ を基準にして考えてみる
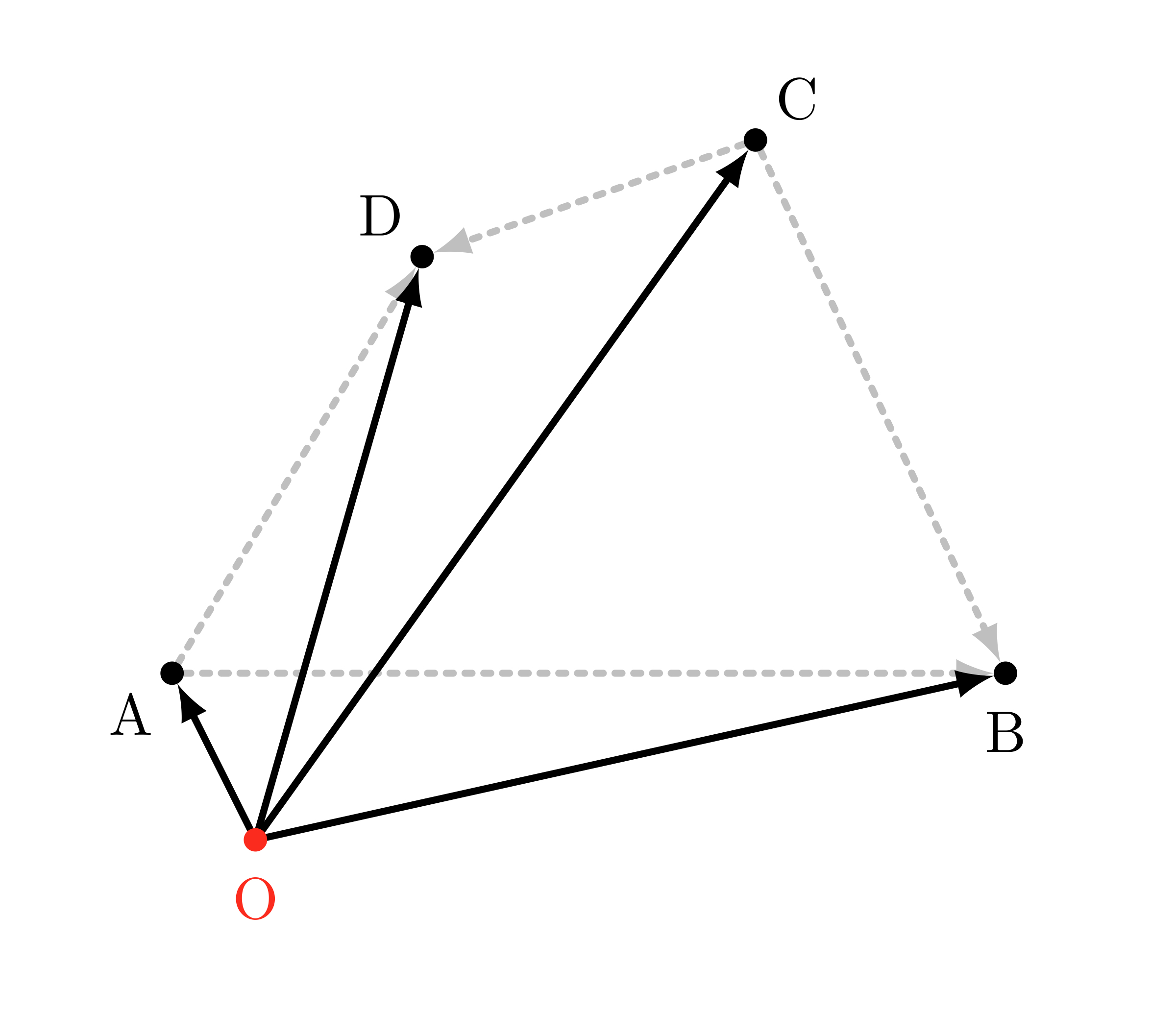
僕「そうそう」
テトラ「先ほどと同じように、計算してみます!
点 $\TT{O}$ を基準にして、
四つのベクトル $\vAB, \vCD, \vAD, \vCB$ をすべて書き換えます。
$$
\begin{cases}
\vAB &= \mvOB - \mvOA \\
\vCD &= \mvOD - \mvOC \\
\vAD &= \mvOD - \mvOA \\
\vCB &= \mvOB - \mvOC \\
\end{cases}
$$
……となります。ということは、
$$
\begin{cases}
\vAB + \vCD &= \underbrace{\mvOB - \mvOA}_{\vAB} + \underbrace{\mvOD - \mvOC}_{\vCD}
= -\mvOA + \mvOB - \mvOC + \mvOD \\
\vAD + \vCB &= \underbrace{\mvOD - \mvOA}_{\vAD} + \underbrace{\mvOB - \mvOC}_{\vCB}
= -\mvOA + \mvOB - \mvOC + \mvOD
\end{cases}
$$
ということです。はい、確かに
$$
\vAB + \vCD = \vAD + \vCB
$$
がいえました! これって、先ほどとほとんど同じです!」
僕「そうだね」
テトラちゃんの気付き
テトラ「先輩……点 $\TT{A}$ を基準にしたときには気付かなかったんですが、
点 $\TT{O}$ を基準にして気が付いたことがあります。
$$
\vAB = \mvOB - \mvOA
$$
ということは、ベクトルの始点と終点に注目すればいいことになります。
始点にはマイナスがついて、終点にはマイナスがつかないからです。
そこで始点と終点に注目して、証明したかった式を見ると……
$$
\vAB + \vCD = \vAD + \vCB
$$
……左辺に出てくる始点は $\TT{A}$ と $\TT{C}$ で、右辺に出てくる始点は $\TT{A}$ と $\TT{C}$ なので同じです。
左辺に出てくる終点は $\TT{B}$ と $\TT{D}$ で、右辺に出てくる終点は $\TT{D}$ と $\TT{B}$ でやっぱり同じ。
なので、これは当たり前……といっていいかどうかわかりませんが、当たり前なのですね」
点の計算
僕「いまテトラちゃんが言ってくれた通りなんだけど、
勝手な点 $\TT{O}$ を基準にするということは、もう《矢印ベクトルの計算》をしているというよりも
《点の計算》をしているように見える。
始点はもう $\TT{O}$ に決まっているから、わざわざいわなくてもいい。つまり、
$$
\begin{cases}
\VECA &= \mvOA \\
\VECB &= \mvOB \\
\VECC &= \mvOC \\
\VECD &= \mvOD
\end{cases}
$$
のようにおく。そうすると、
$$
\begin{align*}
-\VECA + \VECB - \VECC + \VECD &= -\VECA + \VECB - \VECC + \VECD \\
-\mvOA + \mvOB - \mvOC + \mvOD &= -\mvOA + \mvOB - \mvOC + \mvOD \\
-\mvOA + \mvOB - \mvOC + \mvOD &= -\mvOA + \mvOD - \mvOC + \mvOB \\
\vAB + \vCD &= \vAD + \vCB
\end{align*}
$$
のようになって証明できる」
テトラ「はいはい、よくわかります」
矢印の向き
僕「いまのはテトラちゃんの証明を逆にたどっただけだけど、
こんなふうに考えることもできるよ。
テトラちゃんが最初に描いた図を見る」
テトラちゃんの図(再掲)

テトラ「はい。問題文を見ながら描いたものです」
僕「この図で、 $\vCB$ と $\vAD$ の矢印を逆向きにすると、点 $\TT{A}$ からぐるっと一回りできることがわかる。
矢印を逆向きにするというのは始点と終点を交換するということ。
要するに、
$$
\vAB + \vBC + \vCD + \vDA = \vZ
$$
ということ。ここから
$$
\vAB - \vCB + \vCD - \vAD = \vZ
$$
となって、
$$
\vAB + \vCD = \vAD + \vCB
$$
がいえる。いろんな示し方があるね」
ぐるっと一回り
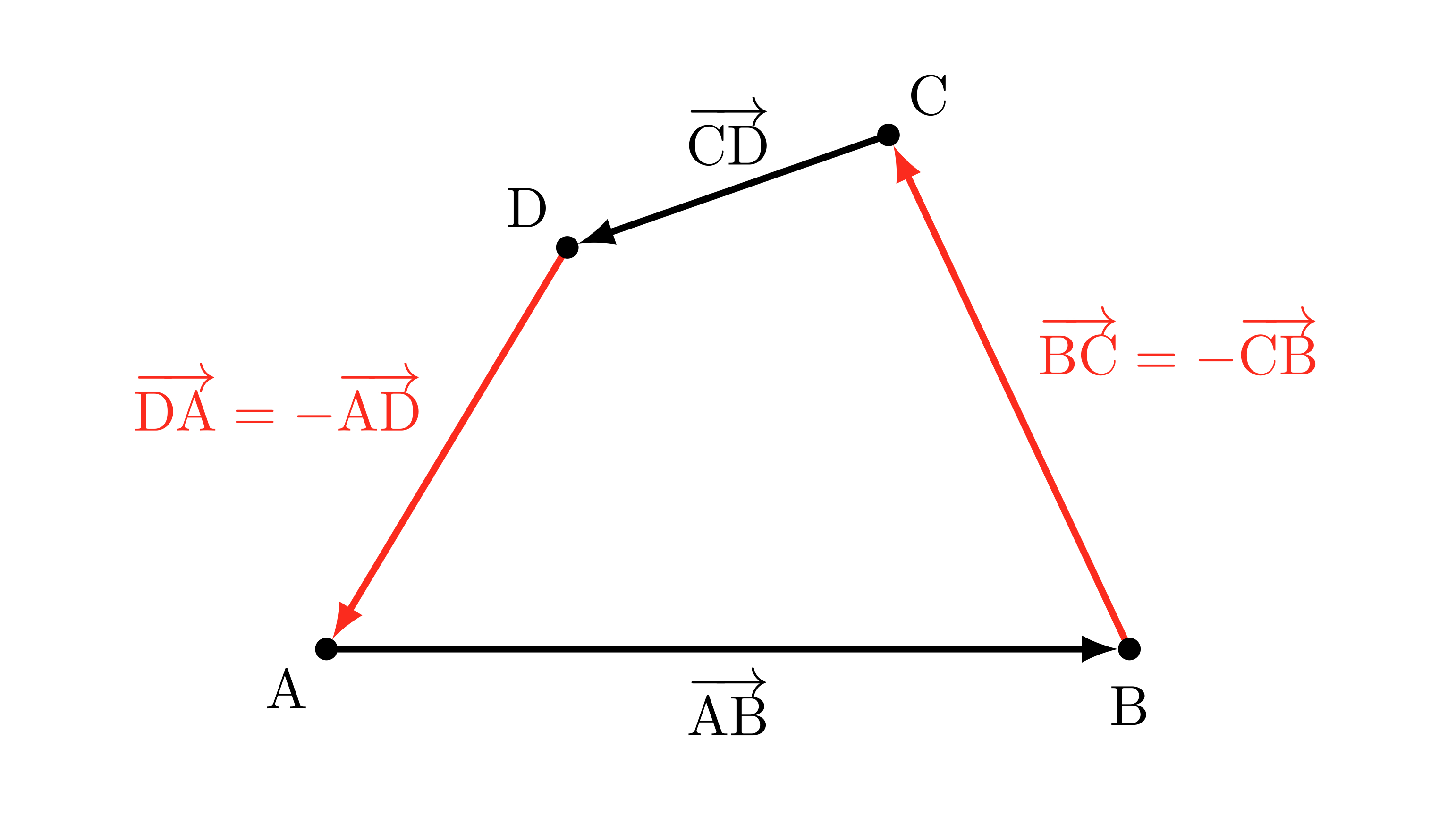
テトラ「言われてみれば、その通りです……あの、でも、先輩? これは、はじめからベクトルの問題ですから、
ベクトルのいろんな使い方ができるというのは、
当たり前のような気がします。
《ベクトルを使う意味》の話から、ちょっとズレちゃいましたよね」
僕「いやいや、実は、ベクトルを使う意味の話はここからなんだ」
テトラ「はい?」
![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」




