$
\newcommand{\TEXT}[1]{\textbf{#1}}
\newcommand{\REMTEXT}[1]{\textbf{#1}}
\definecolor{CUD-GREEN}{rgb}{0.012,0.686,0.478}% 3,175,122
\newcommand{\MARK}[1]{\textcolor{red}{#1}}
\newcommand{\MARKA}[1]{\textcolor{red}{#1}}
\newcommand{\MARKB}[1]{\textcolor{blue}{#1}}
\newcommand{\MARKC}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\GEQ}{\geqq}
\newcommand{\LEQ}{\leqq}
\newcommand{\NEQ}{\neq}
\newcommand{\FOCUS}[1]{\fbox{ $#1$ }}
\newcommand{\REDFOCUS}[1]{\textcolor{red}{#1}}
\newcommand{\GREENFOCUS}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUEFOCUS}[1]{\textcolor{blue}{#1}}
\newcommand{\BROWNFOCUS}[1]{\textcolor{brown}{#1}}
\newcommand{\REDHEART}{\REDFOCUS{\heartsuit}}
\newcommand{\REDTEXT}[1]{\textcolor{red}{#1}}
\newcommand{\GREENTEXT}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUETEXT}[1]{\textcolor{blue}{#1}}
\newcommand{\ABS}[1]{|#1|}
\newcommand{\PHANTOMEQ}{\phantom{{}={}}}
\newcommand{\SQRT}[1]{\sqrt{#1}}
\newcommand{\PS}[1]{\left(#1\right)}
\newcommand{\SGN}{\textrm{sgn}}
\newcommand{\DOTNAME}[1]{\quad\cdots(#1)}
\newcommand{\BAR}[1]{\overline{#1}}
\newcommand{\TRIANGLE}{\triangle}
\newcommand{\TT}[1]{\textrm{#1}}
\newcommand{\TTred}[1]{\textcolor{red}{\textrm{#1}}}
\newcommand{\TTblue}[1]{\textcolor{blue}{\textrm{#1}}}
\newcommand{\ANGLE}[1]{\angle\textrm{#1}}
\newcommand{\TRI}[1]{\triangle\textrm{#1}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\PB}{\TT{PB}}
\newcommand{\BQ}{\TT{BQ}}
\newcommand{\QC}{\TT{QC}}
\newcommand{\CR}{\TT{CR}}
\newcommand{\RA}{\TT{RA}}
\newcommand{\AA}{\TT{AA}}
\newcommand{\AB}{\TT{AB}}
\newcommand{\AC}{\TT{AC}}
\newcommand{\CA}{\TT{CA}}
\newcommand{\AD}{\TT{AD}}
\newcommand{\AE}{\TT{AE}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\AQ}{\TT{AQ}}
\newcommand{\AR}{\TT{AR}}
\newcommand{\PQ}{\TT{PQ}}
\newcommand{\QR}{\TT{QR}}
\newcommand{\BC}{\TT{BC}}
\newcommand{\CA}{\TT{CA}}
\newcommand{\LONGVEC}[1]{\overrightarrow{#1}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vPB}{\LONGVEC{\PB}}
\newcommand{\vBQ}{\LONGVEC{\BQ}}
\newcommand{\vQC}{\LONGVEC{\QC}}
\newcommand{\vCR}{\LONGVEC{\CR}}
\newcommand{\vRA}{\LONGVEC{\RA}}
\newcommand{\vAA}{\LONGVEC{\AA}}
\newcommand{\vAB}{\LONGVEC{\AB}}
\newcommand{\vBC}{\LONGVEC{\BC}}
\newcommand{\vCA}{\LONGVEC{\CA}}
\newcommand{\vDE}{\LONGVEC{\DE}}
\newcommand{\vAD}{\LONGVEC{\AD}}
\newcommand{\vAE}{\LONGVEC{\AE}}
\newcommand{\vAC}{\LONGVEC{\AC}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vAQ}{\LONGVEC{\AQ}}
\newcommand{\vAR}{\LONGVEC{\AR}}
\newcommand{\vPQ}{\LONGVEC{\PQ}}
\newcommand{\vQR}{\LONGVEC{\QR}}
\newcommand{\avAP}{\ABS{\vAP}}
\newcommand{\avPB}{\ABS{\vPB}}
\newcommand{\avBQ}{\ABS{\vBQ}}
\newcommand{\avQC}{\ABS{\vQC}}
\newcommand{\avCR}{\ABS{\vCR}}
\newcommand{\avRA}{\ABS{\vRA}}
\newcommand{\va}{\vec{a}}
\newcommand{\vb}{\BLUEFOCUS{\vec{b}}}
\newcommand{\vc}{\REDFOCUS{\vec{c}}}
\newcommand{\vZ}{\vec{0}}
\definecolor{MUTE-COLOR}{rgb}{0.6,0.6,0.6}%
\definecolor{NOMUTE-COLOR}{rgb}{0.0,0.0,0.0}%
\definecolor{REDNOMUTE-COLOR}{rgb}{1.0,0.0,0.0}%
\newcommand{\MUTE}[1]{\textcolor{MUTE-COLOR}{\TT{#1}}}
\newcommand{\NOMUTE}[1]{\textcolor{NOMUTE-COLOR}{\TT{#1}}}
\newcommand{\REDNOMUTE}[1]{\textcolor{REDNOMUTE-COLOR}{\TT{#1}}}
\newcommand{\mvAA}{\LONGVEC{\MUTE{A}\NOMUTE{A}}}
\newcommand{\mvAB}{\LONGVEC{\MUTE{A}\NOMUTE{B}}}
\newcommand{\mvAC}{\LONGVEC{\MUTE{A}\NOMUTE{C}}}
\newcommand{\mvAP}{\LONGVEC{\MUTE{A}\NOMUTE{P}}}
\newcommand{\mvAQ}{\LONGVEC{\MUTE{A}\NOMUTE{Q}}}
\newcommand{\mvAR}{\LONGVEC{\MUTE{A}\NOMUTE{R}}}
\newcommand{\mvAV}{\LONGVEC{\MUTE{A}\NOMUTE{V}}}
\newcommand{\mvRevAB}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{B}}}
\newcommand{\mvRevAC}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{C}}}
\newcommand{\mvAD}{\LONGVEC{\MUTE{A}\NOMUTE{D}}}
\newcommand{\mvAE}{\LONGVEC{\MUTE{A}\NOMUTE{E}}}
\newcommand{\mvAF}{\LONGVEC{\MUTE{A}\NOMUTE{F}}}
\newcommand{\BP}{\TT{BP}}
\newcommand{\vBP}{\LONGVEC{\BP}}
\newcommand{\NEAREQ}{\fallingdotseq}
\newcommand{\DE}{\TT{DE}}
\newcommand{\CD}{\TT{CD}}
\newcommand{\BE}{\TT{BE}}
\newcommand{\AF}{\TT{AF}}
\newcommand{\BF}{\TT{BF}}
\newcommand{\BE}{\TT{BE}}
\newcommand{\CF}{\TT{CF}}
\newcommand{\CD}{\TT{CD}}
\newcommand{\AG}{\TT{AG}}
\newcommand{\BG}{\TT{BG}}
\newcommand{\vAF}{\LONGVEC{\AF}}
\newcommand{\vBF}{\LONGVEC{\BF}}
\newcommand{\vBE}{\LONGVEC{\BE}}
\newcommand{\vCF}{\LONGVEC{\CF}}
\newcommand{\vCD}{\LONGVEC{\CD}}
\newcommand{\vAG}{\LONGVEC{\AG}}
\newcommand{\vBG}{\LONGVEC{\BG}}
\newcommand{\NONAMACROBASE}[2]{\texttt{..}{\scriptstyle #1}#2}
\newcommand{\NONAMACROBASEREV}[2]{#1{\scriptstyle #2}\texttt{..}}
\newcommand{\NONAMACRO}[1]{\NONAMACROBASE{#1}{#1}}
\newcommand{\NONAMACROREV}[1]{\NONAMACROBASEREV{#1}{#1}}
\newcommand{\NONA}{\NONAMACROBASE{\textrm o}{\textrm O}}
\newcommand{\NONAX}{\NONAMACROBASE{\textrm x}{\textrm X}}
\newcommand{\NONAQ}{\NONAMACRO{?}}
\newcommand{\NONAQREV}{\NONAMACROREV{?}}
\newcommand{\NONAEX}{\NONAMACRO{!}}
\newcommand{\NONAHEART}{\NONAMACRO{\heartsuit}}
$
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。
好奇心旺盛で根気強い《元気少女》。言葉が大好き。
図書室にて
テトラ「おもしろいですっ! 秘密の宝物を発見したみたいですね……」
僕「秘密の宝物?」
ここは高校の図書室。いまは放課後。
僕は後輩のテトラちゃんと話をしていた。
いとこのユーリといっしょに証明したメネラウスの定理についてだ(第431回参照)。
テトラ「はい、そうです。メネラウスの定理で $1$ になるところが、
ベクトルを使うと $-1$ になる。
それは《向きも考えたメネラウスの定理》や《外分点の個数も考えたメネラウスの定理》
のように解釈できる……すごく、おもしろいと思いますっ!(第434回参照)」
テトラちゃんはそういうと、元気よく両手を挙げた。
きっと、おもしろさを表現しているのだろう。
僕「うん、そうだよね。僕も知らなかったよ。
たまたま、メネラウスの定理をベクトルで証明して気付いたんだけどね」
テトラ「あたしも、その場でユーリちゃんといっしょに考えてみたかったです……」
テトラちゃんはそういうと、眉根を寄せて口をとがらせた。
今度は、不満を表現しているのだろう。
僕「じゃあ、いっしょに考える?」
テトラ「え?」
僕「いま話したのはメネラウスの定理の証明だけど、
後でベクトルを使って考えてみようと思ってた図形の問題があるんだよ。
そんなに難しくないと思うな」
テトラ「はいはいはいはいっ! ぜひぜひぜひぜひっ!」
テトラちゃんは右手を大きく挙げて、身を乗り出してきた。
そんなふうにして、
僕はテトラちゃんといっしょに図形の問題を考えることになった。
図形の問題で最初にやることは?
僕「こういう問題だよ」
問題
平面上に三角形 $\TT{ABC}$ がある。
辺 $\BC$ と平行な直線が、
直線 $\AB,\AC$ と交わる点をそれぞれ点 $\TT{D},\TT{E}$ とする。
線分 $\CD$ と線分 $\BE$ の交点を $\TT{F}$ とする。
直線 $\AF$ と辺 $\BC$ の交点を $\TT{G}$ とする。
このとき、点 $\TT{G}$ は辺 $\BC$ の中点であることを証明せよ。
参考:モノグラフ『ベクトル』(科学新興社)

テトラ「なるほどです。
これをベクトルを使って証明すればいいんですよね。
三つのベクトル $\vAB$ と $\vBC$ と $\vCA$ を考えて——」
僕「おっとっと! テトラちゃん、ちょっと待って!」
テトラ「はい?」
僕「考え始めようとしているのに止めちゃってごめんね。
ベクトルを使うかどうかによらず、
図形の問題の最初は、ちゃんとセオリー通りに進もうよ」
テトラ「セオリー通りといいますと?」
僕「図形の問題が出たときに、一番最初にやることは何?」
テトラ「一番最初にやること……ああ、図を描くことですか!」
僕「そうだね。
《図をかけ》
はポリアの『いかにして問題をとくか』にもある。大事だよね」
テトラ「失礼しました。先輩の解き方を見ていて、
あたしもベクトルを使って《腕力》を振るう計算をするつもりでしたので、
つい先走りをしてしまいました。
図を描かずに図形の問題を考え始めるのは無茶ですね」
僕「図を一歩一歩描いていくのは、問題を把握するためにも有効だし」
テトラ「では、問題を読みながら、一歩一歩描いていきますっ!」
図を描こう
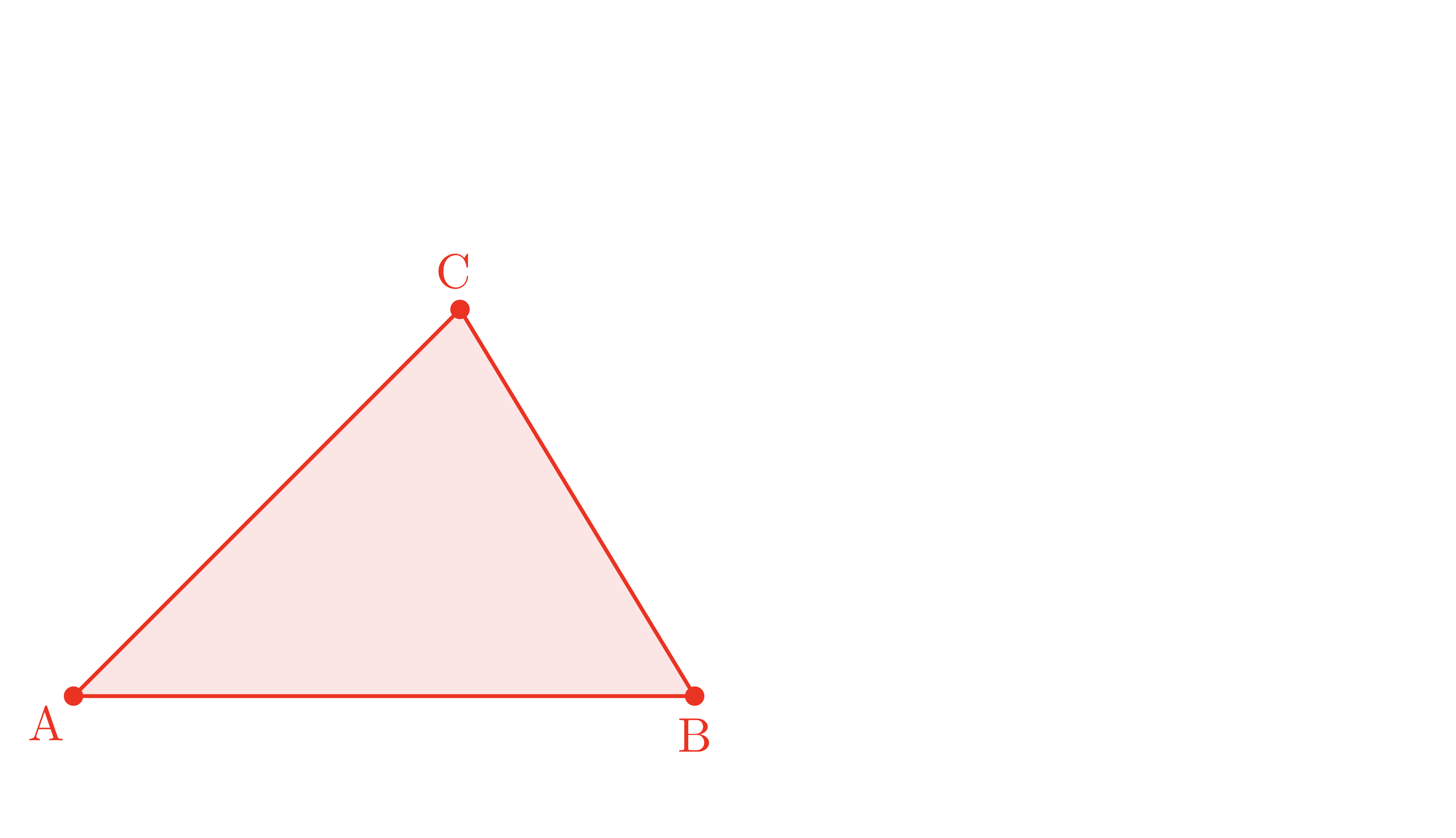
【1歩目】(三角形 $\TT{ABC}$)
平面上に三角形 $\TT{ABC}$ がある。
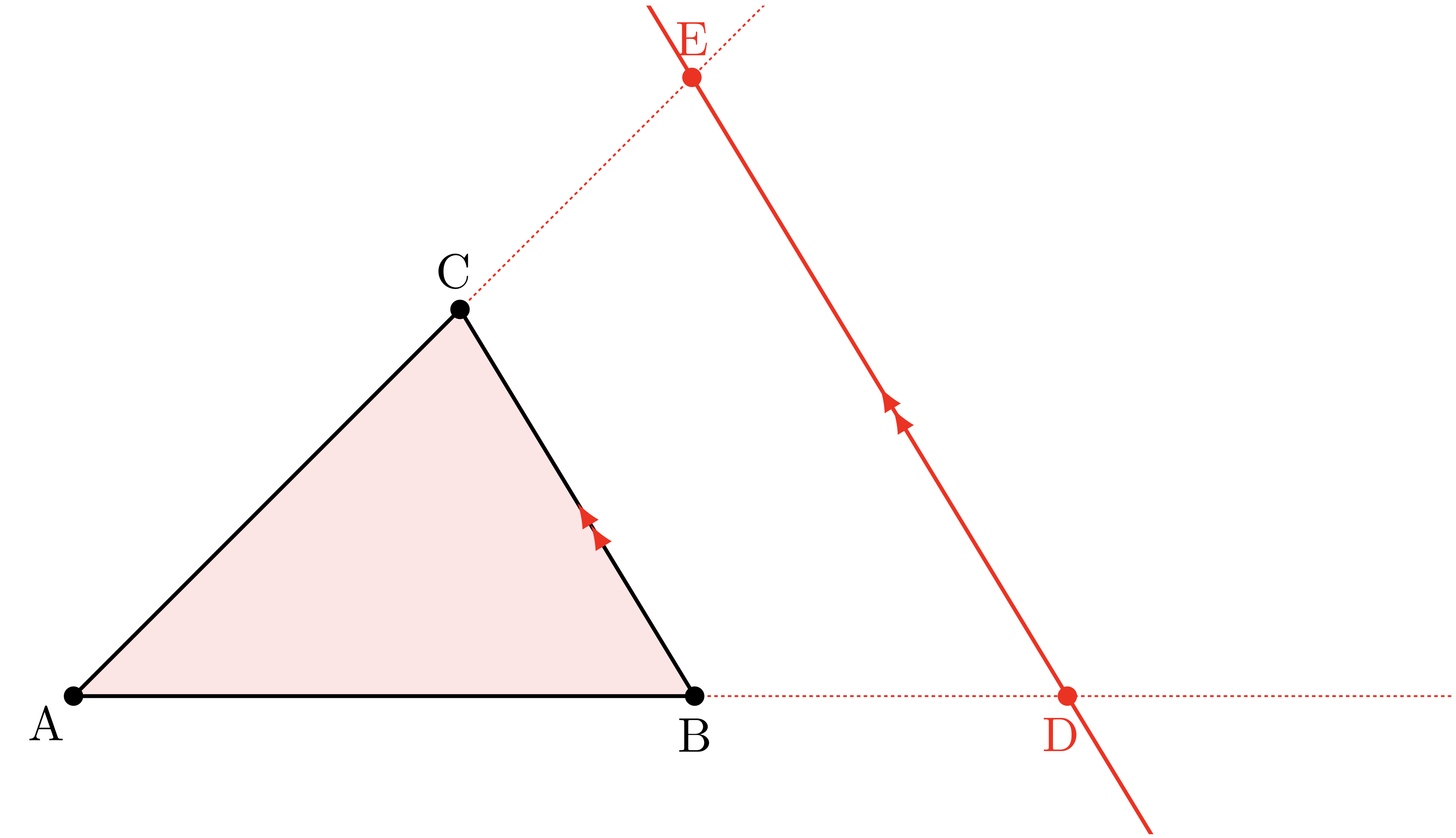
【2歩目】(二点 $\TT{D},\TT{E}$)
辺 $\BC$ と平行な直線が、
直線 $\AB,\AC$ と交わる点をそれぞれ点 $\TT{D},\TT{E}$ とする。
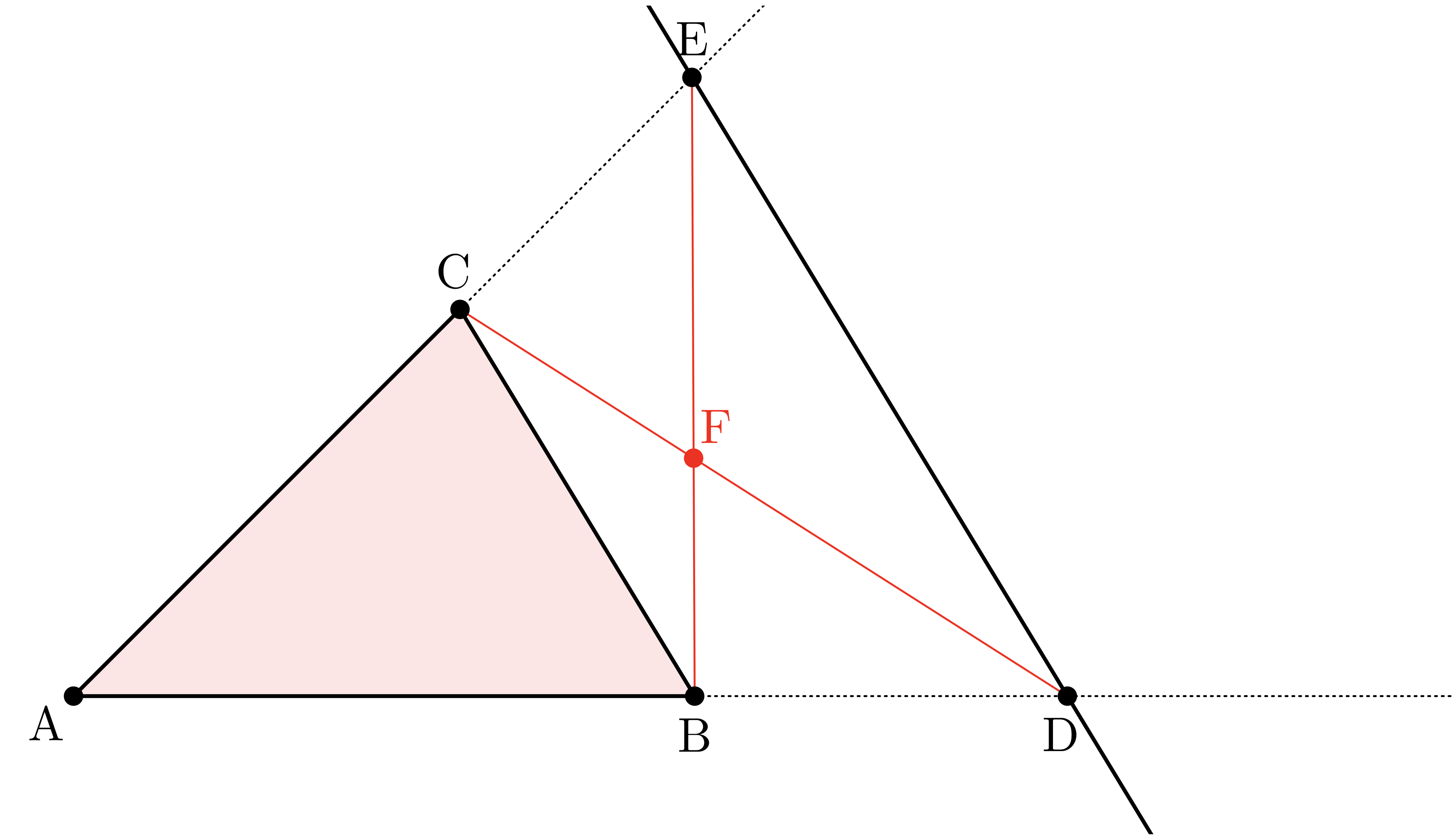
【3歩目】(点 $\TT{F}$)
線分 $\CD$ と線分 $\BE$ の交点を $\TT{F}$ とする。
【4歩目】(点 $\TT{G}$)
直線 $\AF$ と辺 $\BC$ の交点を $\TT{G}$ とする。
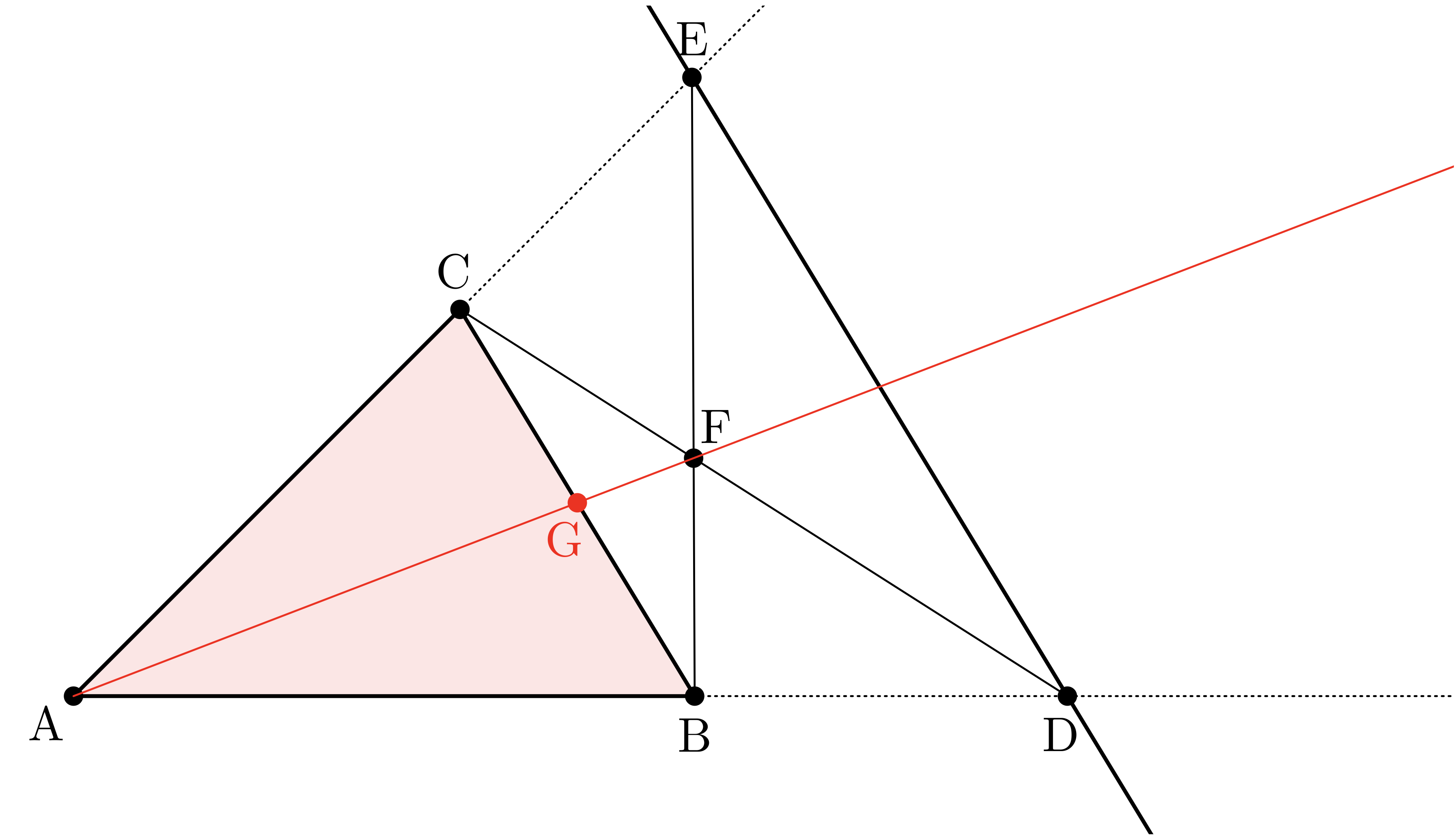
【5歩目】(点 $\TT{G}$ は辺 $\BC$ の中点?)
このとき、点 $\TT{G}$ は辺 $\BC$ の中点であることを証明せよ。
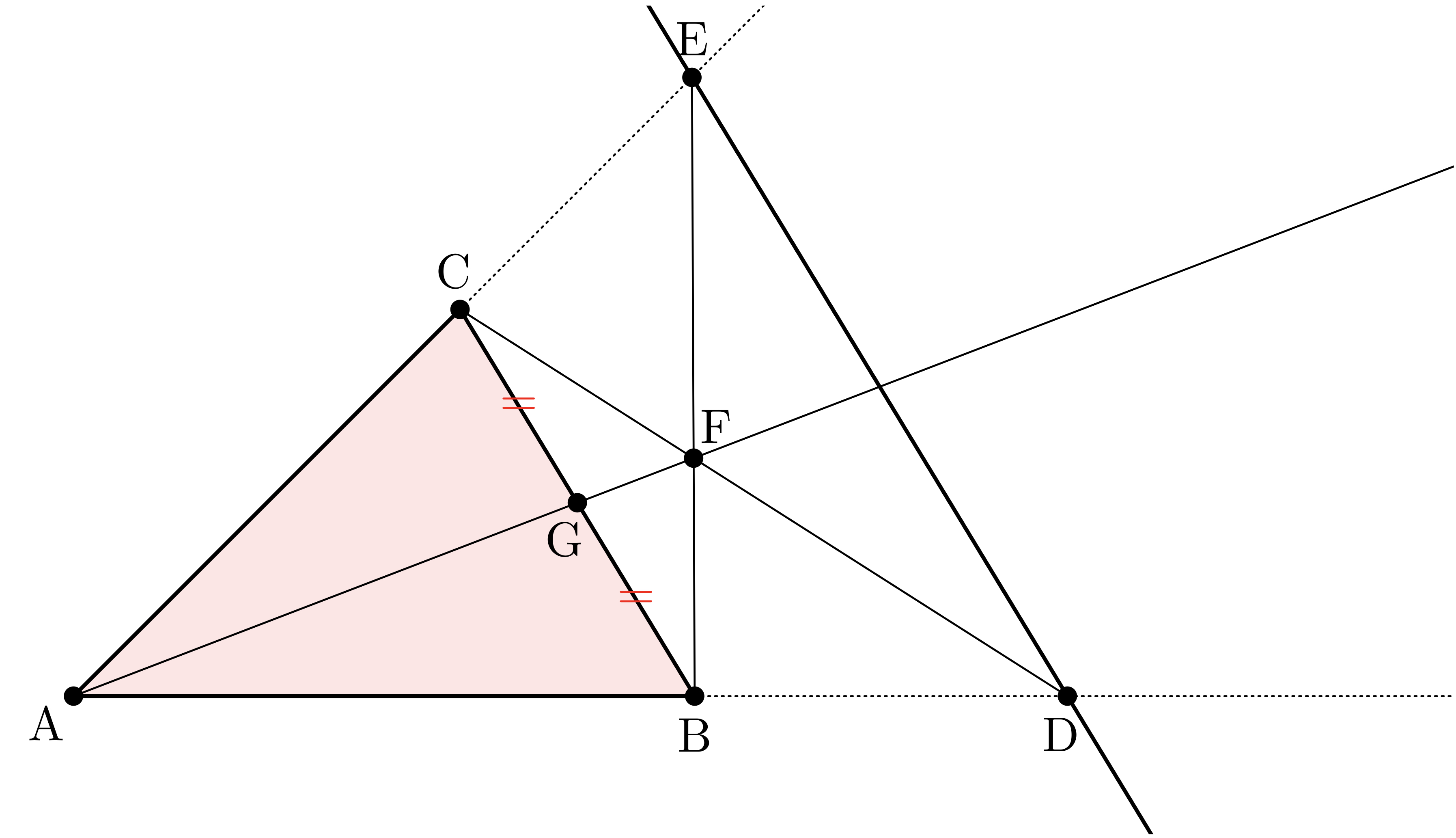
テトラ「確かに、一歩一歩図を描いていくと、わかってきますね。
どのようにしてその点が生まれたか、それがわかります」
僕「うん。これで図が描けた。
次にどんなふうに考える?」
見つかる
テトラ「あのですね……図を描いているうちに、
相似な三角形が見つかりました」
僕「どれのこと?」
テトラ「今回の証明に関係があるかどうかわからないんですけど、
$\BC$ と $\DE$ が平行ですから、
二つの三角形 $\TRI{ABC}$ と $\TRI{ADE}$ が相似になると思います。
それは三つの角がすべて等しいからです」
相似な三角形 $\TRI{ABC}$ と $\TRI{ADE}$ が見つかった
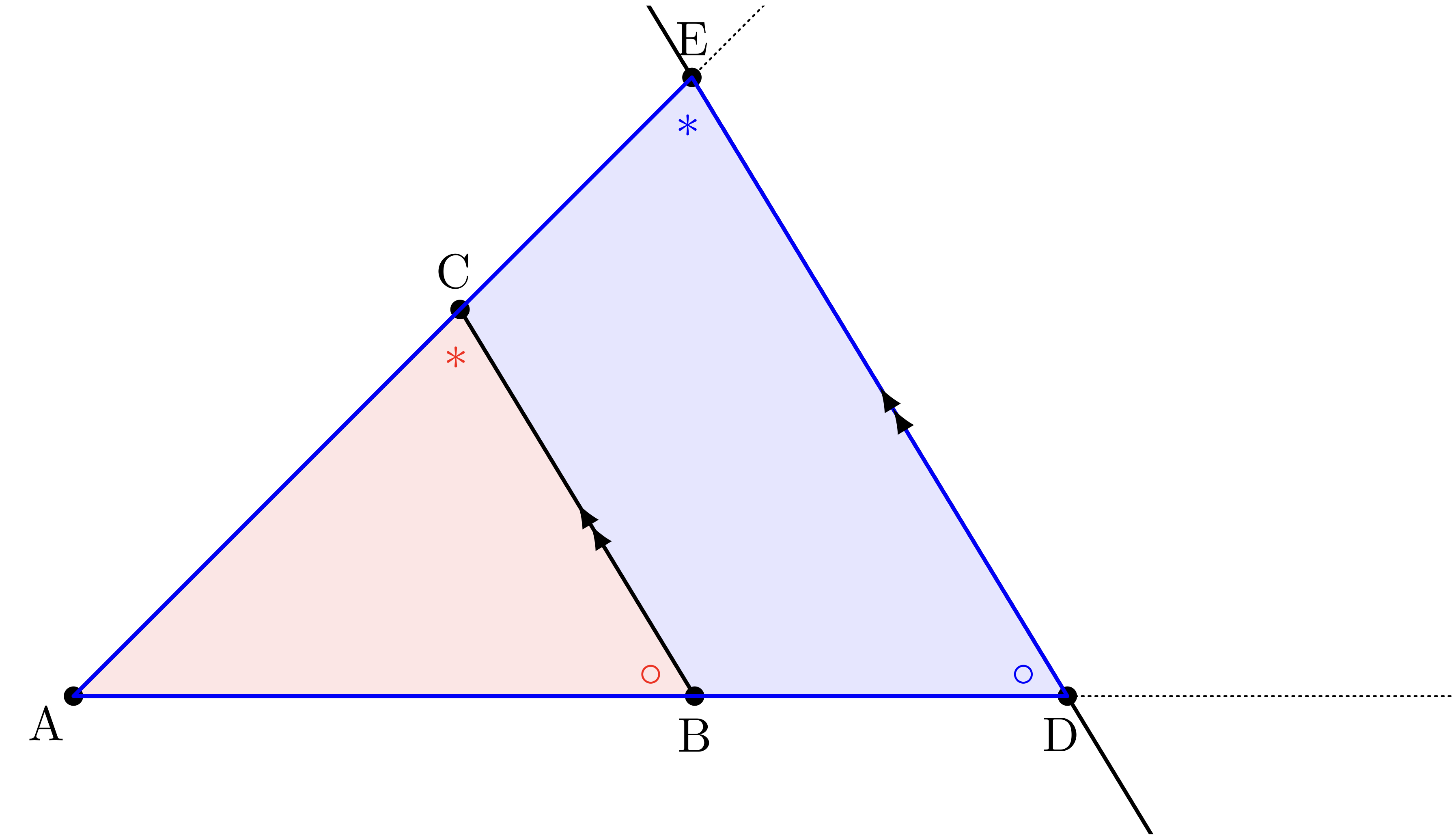
僕「なるほど。確かにその二つの三角形は相似になるね。
まず $\ANGLE{A}$ は共通。
そして $\BC$ と $\DE$ は平行だから、 $\ANGLE{B} = \ANGLE{D}$ と $\ANGLE{C} = \ANGLE{E}$ になる。同位角だ」
テトラ「はい。三つの角がそれぞれ等しいので、 $\TRI{ABC}$ と $\TRI{ADE}$ は相似になります」
僕「その他にも、何か見つかったものはある?」
テトラ「いえ、そのくらいですね……」
と、ここでテトラちゃんは軽く爪を噛んで考え始めた。
テトラ「あたしは、図形の問題をどんな風に考えているんでしょう……」
僕「うん?」
テトラ「先輩から『次は何を考える?』や『何か見つかったものはある?』のように尋ねていただくと、
あたしは、自分の考える道筋を意識します。
あたしって、普段どんな風に考えているんでしょうね。
図形の問題……特に証明の問題を考えるとき、
あたしは適当な三角形や直線を注目して、
何か成り立つことが見つからないかなあ、
と考えているみたいです。
自分が知っている公式や定理に合うものが見つかりますように、と願いつつ。
図形の問題は、嫌いではないですけれど難しいと思います」
僕「決まり切った方法はないから、
ある程度は試行錯誤しないといけないと思うよ。
補助線が必要になると、さらに難しくなる」
テトラ「そうっ! 本当にそうです!」
【CM】
ユーリ「はい、ここでCMでーす。
三角形の合同、相似、証明の書き方と考え方。そして平行線の公理まで。
図形の証明はこちらをどーぞ!」
ノナ「どうぞ $\NONAHEART$」
テトラ「あ、でも、ベクトルを使うと計算に持ち込めるので、
補助線を見つける《ひらめき》は要らなくなるんでしょうか?」
僕「ユーリと話しているときもその話題になった(第432回参照)けど、
《ひらめき》が要らなくなるというのは言い過ぎだし、
ベクトルを機械的に当てはめると、それこそ計算がものすごく大変になっちゃうから難しいよね」
テトラ「がんばって根気よく計算すれば必ず解けるとしたら、うれしいですけれど……」
僕「テトラちゃんはかなり《腕力》があるからね」
テトラ「そ……それは計算の話ですよね? 《腕力》?」
テトラちゃんは真面目な顔で腕を曲げ、力こぶを作るジェスチャをして僕を見る。
そして、僕たちは大笑いした。
ベクトルを使って考えていこう
僕「じゃあ、今回の問題を、ベクトルで表しながら考えていく?」
問題(再掲)
平面上に三角形 $\TT{ABC}$ がある。
辺 $\BC$ と平行な直線が、
直線 $\AB,\AC$ と交わる点をそれぞれ点 $\TT{D},\TT{E}$ とする。
線分 $\CD$ と線分 $\BE$ の交点を $\TT{F}$ とする。
直線 $\AF$ と辺 $\BC$ の交点を $\TT{G}$ とする。
このとき、点 $\TT{G}$ は辺 $\BC$ の中点であることを証明せよ。
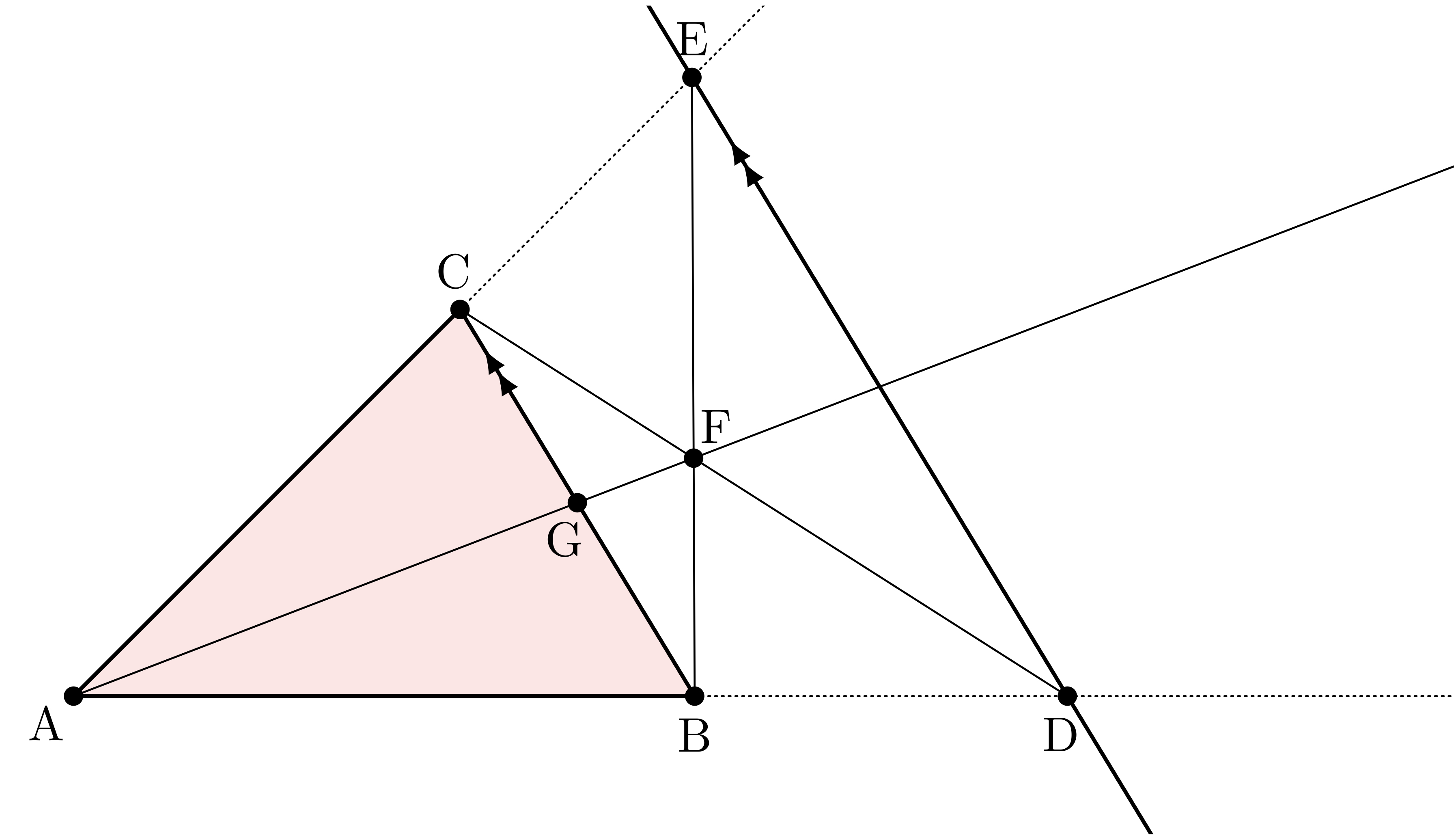
参考:モノグラフ『ベクトル』(科学新興社)
テトラ「はい。点がたくさんありますから、ベクトルもたくさん出来ますね。 $\vAB,\vBC,\vCA,\ldots$」
僕「そうだね。でも闇雲にベクトルを考えていると、それこそ混乱してしまう」
テトラ「思ったんですけれど、図を一歩一歩描いたときと同じく、
一歩一歩考えてみるというのはどうでしょう」
僕「なるほど」
【1歩目】三角形
テトラ「まず【1歩目】の $\TRI{ABC}$ はいいですよね。特に条件はありませんから。
【1歩目】(三角形 $\TT{ABC}$)
平面上に三角形 $\TT{ABC}$ がある。

僕「ところがね、テトラちゃん。
すごく大事なことがここで出てくる」
テトラ「三角形があるだけで、ですか?」
![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」








