第423回 シーズン43 エピソード3

どこまで分解できるかな？（前編）

僕の部屋

ユーリ「ユーリ、因数分解は完璧だよ！　もっと難しい問題、出してよ！」

僕「頼もしいなあ。じゃあ、これを因数分解してみる？」

ユーリ「どらどら……？」

僕「できるだけ、でいいからね」

ユーリ「んー、これも因数定理使えばいいわけじゃん？」

僕「何を使ってもいいよ。因数分解できれば」

ユーリ「試しに $1$ を入れてみる！」

僕「……」

$x$ に $1$ を代入してみる

ユーリ「じゃ、やってみるねー。 $x$ に $1$ を代入すると……やったー！ $0$ になったよ！」

$$ \begin{align*} &\PHANTOMEQ x^4 - 10x^3 + 26x^2 -10x + 25 \\ &= 1^4 - 10\times1^3 + 26\times1^2 - 10\times1 + 25 && \REMTEXT{$x$に$1$を代入}\\ &= 1 - 10 + 26 - 10 + 25 \\ &= \textbf{やったー！$0$になったよ（？）} \end{align*} $$

僕「ちょっと待って。ユーリ、どうして $$ 1 - 10 + 26 - 10 + 25 $$ が $0$ になるんだ？」

ユーリ「ありり？　いやあー勘違い勘違い。 $1$ と $26$ と $25$ とマイナスがちらちら見えたから、 頭の中で $1+25$ と $-26$ を計算しちゃったぜ」

僕「『計算しちゃったぜ』じゃないよ」

ユーリ「でも、そーゆーこと、あるよね。 $0$ になってほしい！……というキミの強い願いが心を動かすんだ」

僕「そんな感動ドラマっぽく言われても、単なる計算ミスだからね」

ユーリ「ちぇっ……ともかく、 $x$ に $1$ を入れても $0$ になりませんでしたー」

$$ \begin{align*} &\PHANTOMEQ x^4 - 10x^3 + 26x^2 -10x + 25 \\ &= 1^4 - 10\times1^3 + 26\times1^2 - 10\times1 + 25 && \REMTEXT{$x$に$1$を代入}\\ &= 1 - 10 + 26 - 10 + 25 \\ &= 32 \\ &\NEQ 0 \end{align*} $$

僕「そうだね。次は何を試す？」

ユーリ「$1$ の次は $2$ を代入してみるー！」

僕「え？　それはなぜ？」

ユーリ「え？　それはダメ？」

僕「……僕だったら、別の数を試すからね」

ユーリ「別の数？　試しにいろんな数を $x$ に入れてみて、 $$ x^4 - 10x^3 + 26x^2 -10x + 25 $$ が $0$ になる数を見つけるんだよね？」

僕「そうだね。 $a$ を入れて $0$ になれば、 $x-a$ が因子になる」

ユーリ「あー、そかそか。 $$ x^4 - 10x^3 + 26x^2 -10x + 25 = (x-a)(x-b)(x-c)(x-d) $$ みたいな形にするんだった。 $a,b,c,d$ を掛けたら $25$ になるはずだから、 つまり、 $$ abcd = 25 $$ のはず。だったら、 $2$ はありえない！」

僕「いや、『ありえない』は言い過ぎだけど、 $2$ よりも先に試したい数はある」

ユーリ「掛けて $25$ になる数だから、たとえば $5$ だ！」

僕「うん。僕だったらそれを試す。 $25$ の約数をまず試す。 符号も考えると、 $$ +1\qquad -1\qquad +5\qquad -5\qquad $$ を試すかな。 $25$ を試してもいいけど、 $1$ と $-1$ を先に試してダメだったら、 $25$ もたぶんダメ」

ユーリ「そっか。マイナスもあるね。んじゃ、 $-1$ を試してみる！」

$x$ に $-1$ を代入してみる

$$ x^4 - 10x^3 + 26x^2 -10x + 25 $$

ユーリ「$x$ に $-1$ を入れたら……あっ、ダメだ！　 $0$ にならない！」

僕「ユーリ、判断が早い」

ユーリ「ユーリは鱗滝（うろこだき）さんにホメられた！」

僕「鬼滅ネタやめい」

ユーリ「だって、マイナスついてるのが $-10x^3$ と $-10x$ だけだもん。 偶数乗の $x$ しか残ってない」

僕「おお、冴えてるなあ。 そうだね。 $$ x^4 - 10x^3 + 26x^2 -10x + 25 $$ の $x$ に $-1$ を代入したら、 《$x$ の偶数乗》は $1$ で《$x$ の奇数乗》は $-1$ になる。 ところが、《$x$ の偶数乗》になってる項の係数はぜんぶプラスで、 《$x$ の奇数乗》になってる項の係数はぜんぶマイナス。 だから、この式の値は必ずプラスになる」

$$ \begin{array}{ccccllll} x^4 &- 10x^3 &+ 26x^2 &-10x &+ 25 & \\ \REDFOCUS{x^4} & &\REDFOCUS{+ 26x^2} & &\REDFOCUS{+ 25} & \REDFOCUS{\textrm{$x$の偶数乗}}\\ &\BLUEFOCUS{- 10x^3} & & \BLUEFOCUS{-10x} & & \BLUEFOCUS{\textrm{$x$の奇数乗}} \end{array} $$

ユーリ「そーゆーこと！」

僕「そして実際、計算すると……

$$ \begin{align*} &\PHANTOMEQ x^4 - 10x^3 + 26x^2 -10x + 25 \\ &= (-1)^4 - 10\times(-1)^3 + 26\times(-1)^2 - 10\times(-1) + 25 && \REMTEXT{$x$に$-1$を代入}\\ &= 1 + 10 + 26 + 10 + 25 \\ &\NEQ 0 \end{align*} $$

……確かに $0$ にならない」

ユーリ「あっ、てことは $x$ に $-5$ を入れるのもダメか。じゃあ、次は $5$ を入れてみる！」

$x$ に $5$ を代入してみる

僕「今度はどうかな？」

$$ \begin{align*} &\PHANTOMEQ x^4 - 10x^3 + 26x^2 -10x + 25 \\ &= 5^4 - 10\times5^3 + 26\times5^2 - 10\times5 + 25 && \REMTEXT{$x$に$5$を代入}\\ &= \textbf{（けっこうめんどい……）} \\ \end{align*} $$

ユーリ「あ、けっこうめんどい……ええと、 $5^4$ って $25\times25$ だから——」

僕「$25$ でくくれそうだよ。だって……

• $5^4 = 5^2 \times 5^2 = 25\times \REDFOCUS{25}$
• $10\times 5^3 = 10\times5\times5^2 = 50\times\REDFOCUS{25}$
• $26\times 5^2 = 26\times\REDFOCUS{25}$
• $10\times5 = 2\times5\times5 = 2\times\REDFOCUS{25}$
• $25 = 1\times\REDFOCUS{25}$

$$ \begin{align*} &\PHANTOMEQ x^4 - 10x^3 + 26x^2 -10x + 25 \\ &= 5^4 - 10\times5^3 + 26\times5^2 - 10\times5 + 25 && \REMTEXT{$x$に$5$を代入}\\ &= 25\times\REDFOCUS{25} - 50\times\REDFOCUS{25} + 26\times\REDFOCUS{25} - 2\times\REDFOCUS{25} + 1\times\REDFOCUS{25} && \REMTEXT{$25$を見つける} \\ &= (25 - 50 + 26 - 2 + 1)\times\REDFOCUS{25} && \REMTEXT{$25$でくくる} \\ &= (52 - 52)\times\REDFOCUS{25} \\ &= 0 \end{align*} $$

ユーリ「なんと小賢しいワザを使いおって……」

僕「いや、もちろん真面目に計算してもいいけど、 $10\times5$ や $25$ が見えていたら $5^2 = 25$ でくくれそうだとわかる」

ユーリ「ふみゅー」

僕「ともかく、 $5$ を代入したら $0$ になった」

ユーリ「そーだよ！　ユーリが問題解いてたんじゃん！　 $x - 5$ で $x^4 - 10x^3 + 26x^2 -10x + 25$ を割る！」

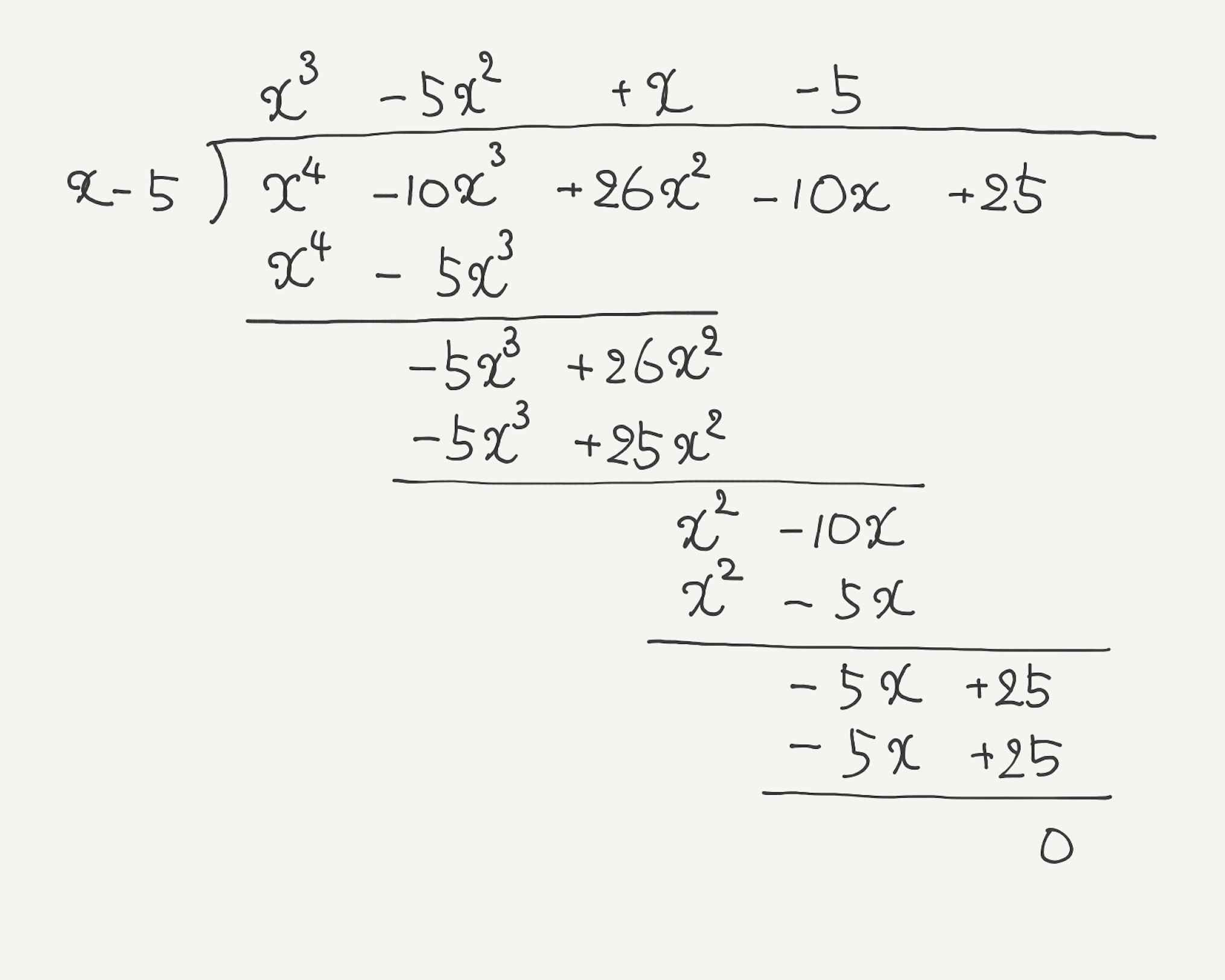
僕「うん、うまく割り切れたね。これで、 $$ x^4 - 10x^3 + 26x^2 -10x + 25 = (x-5)(x^3 - 5x^2 + x - 5) $$ までできた。さてさて、ユーリ先生、次の一手は？」

ユーリ「そりゃもちろん、$\REDFOCUS{\textrm{ココ}}$んとこを因数分解するんだけど……」

$$ x^4 - 10x^3 + 26x^2 -10x + 25 = (x-5)(\,\underbrace{\REDFOCUS{x^3 - 5x^2 + x - 5}}_{\REDFOCUS{\textrm{ココ}}}\,) $$

僕「じゃあ、また $x$ に $1$ を代入して因数定理を使う？」

ユーリ「……んにゃ、違うね！　その手には乗りませんよーだ！（ベー）」

僕「おお」

ユーリ「だって、左辺の $x^4 - 10x^3 + 26x^2 -10x + 25$ で $1$ を代入して $0$ にならなかったんだから、 右辺の $\REDFOCUS{x^3 - 5x^2 + x - 5}$ に $1$ を代入しても $0$ になるはずない！　……でしょ？」

僕「ご明察」

ユーリ「……」

僕「だったら、ユーリは何を悩んでるんだろう」