第424回 シーズン43 エピソード4

どこまで分解できるかな？（後編）

どこまで因数分解？

僕「……うん、だからね。この二つの因数分解はどちらも正しいんだ」

ユーリ「どっちも正しい……なんてことあんの？」

僕「うん、あるよ。《係数としてどんな数を使うか》という前提をつけてやれば、 どちらも正しい因数分解といえる。 係数として実数を使うか、それとも複素数を使うかということ」

ユーリ「へー」

僕「係数として実数を使った場合は、 $$ x^4 - 10x^3 + 26x^2 -10x + 25 = (x-5)(x-5)(x^2 + 1) $$ で因数分解は終わっている。 $x^2 + 1$ は係数が実数である $1$ 次式の積で表すことはできないから、 これ以上は因数分解できない」

ユーリ「$x$ が実数だと、 $x^2 + 1$ は $0$ にならないから（第423回参照）」

僕「そういうこと。そこでユーリは虚数単位 $i$ を持ち出してきた。 それは、係数を実数の範囲で考えるんじゃなくて、複素数まで広げて考えたことになる。 これはすばらしいアイディアだよ、ユーリ」

ユーリ「いやー、それほどでもあるよ」

僕「あるんかい。……複素数まで広げれば、 虚数単位 $i$ が使える。そして $x^2 + 1$ で $x$ に $i$ を代入すれば $x^2 + 1 = 0$ になる。 $i^2 = -1$ だから。 もちろん、 $x$ に $-i$ を代入してもいい。 だから、 係数として複素数まで使って構わないとした場合は、 $$ x^4 - 10x^3 + 26x^2 -10x + 25 = (x-5)(x-5)(x-i)(x+i) $$ まで因数分解ができる。これで、一次式の積に分解できたことになる。 因数分解を考えるときは、 そういうふうに係数にどんな数を使えるかをちゃんと決めてあげないといけないんだ。本当はね」

ユーリ「そんなの、知らなかった……」

僕「そうだね。学校で式の計算を練習しているときには、 あまりうるさくいわないから」

ユーリ「複素数とか出てこないし」

僕「いやいや、因数分解を考えるのは、実数や複素数に複素数に限らない話だよ」

ユーリ「そーなの？」

有理数係数の多項式

僕「たとえば、多項式の係数を有理数の範囲で考えてみる。 有理数（ゆうりすう）はわかるよね」

ユーリ「有理数はユーリの数ですぜ、ダンナ」

僕「誰がダンナじゃ」

ユーリ「有理数は、分数で——《整数分の整数》で表せる数でしょ？　ただし、ゼロで割っちゃダメ」

僕「そうだね。 $a$ と $b$ を整数として、 $b \NEQ 0$ としたとき、 $$ \frac{a}{b} $$ という分数で表せる数が有理数。 $\tfrac12$ や $\tfrac{-123}{45}$ は有理数だけど、 円周率や $\SQRT2$ は有理数じゃない」

ユーリ「わかってるって」

僕「じゃ、 $0.5$ は有理数かな」

ユーリ「もちろん有理数だよん。だって $0.5 = \tfrac12$ だから」

僕「そうだね。 そして、整数の $123$ も有理数といえる。 $123 = \tfrac{123}{1}$ だから。 整数は有理数でもあるし、有理数は実数でもあるし、実数は複素数でもある。 要するに、整数、有理数、実数、複素数はこんな関係にある」

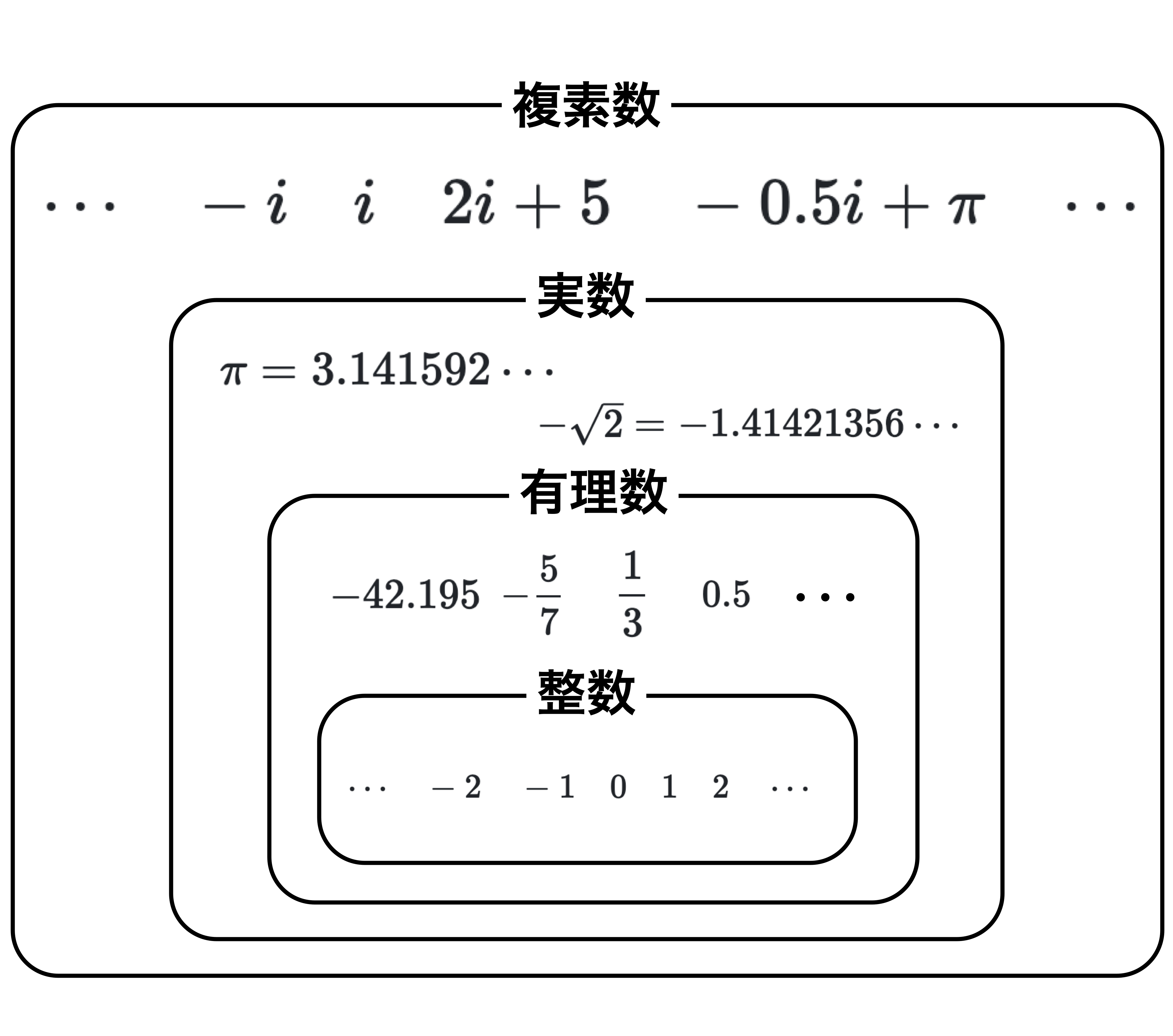
ユーリ「ふんふん！」

僕「じゃ、ここからは多項式の係数には有理数しか使えないことにして考えてみよう」

ユーリ「ふんふん？」

僕「そのとき、 $x^2 - 2$ という多項式は有理数係数の一次式に因数分解できる？」

ユーリ「なーるほど。お兄ちゃんが言いたいこと、わかったよ」

僕「おお」

ユーリ「因数定理で考えると、 $$ x^2 - 2 = 0 $$ になる $x$ を見つければ、因数分解できるはず。 $x^2 - 2$ は、 $$ x = \SQRT2 $$ とか $$ x = -\SQRT2 $$ ならゼロになる！　だけど、 $\SQRT2$ と $-\SQRT2$ はどっちも有理数じゃない。 だから、 $x^2 - 2$ は有理数係数の一次式には因数分解できない！」

僕「その通り！　有理数（・・・）係数で考えると、 $x^2 - 2$ はもうこれ以上因数分解できないね。 だけど、実数（・・）係数で考えると一次式まで因数分解できる。実際、 $$ x^2 - 2 = (x-\SQRT2)(x+\SQRT2) $$ のように因数分解できる。 だから因数分解では、係数をどういう種類の数で考えているのかを意識しないと本当はまずいんだ」

ユーリ「$x^2 - 2$ がこれ以上因数分解できるかどうかって、 $x^2 + 1$ が因数分解できるかどうかとそっくりだね」

僕「そうだね。 $x^2 - 2$ と $x^2 + 1$ はどちらも、 $$ x^2 - A $$ という形をしているといえる。 そう考えると、二つの多項式は《同じ形》といえるね」

• $x^2 - 2$ は、 $x^2 - A$ で $A = 2$ にしたものである。
• $x^2 + 1$ は、 $x^2 - A$ で $A = -1$ にしたものである。

ユーリ「ははーん……待って待って。 その $A$ って、 《二乗したら $2$ になる数》と《二乗したら $-1$ になる数》に出てくる $2$ とか $-1$ のことだよね？」

僕「そういうこと」

ユーリ「……」

僕「……」

ユーリ「……ねー、もしも $4$ だったら？」

僕「$x^2 - A$ の $A$ が $4$ だったら、ってこと？　そりゃもちろん、有理数係数の一次式に因数分解できるよ。 《二乗したら $4$ になる数》を考えることになるから、 $2$ と $-2$ が使える。 $2$ と $-2$ は有理数だから、 一次式の積で表すためには、係数を有理数で考えればいい。実数まで数の範囲を広げる必要はない」

ユーリ「整数でも良くね？」

僕「おっ」

ユーリ「$2$ と $-2$ は整数だから……」

僕「ユーリはすごいな！　確かにそうだね。 $x^2 - 4$ は整数係数で考えたとき、 $x - 2$ と $x + 2$ の積に因数分解できる」

ユーリ「だよね！　こーゆーの、考えてたの」

僕「なるほど？」