![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
『群論への第一歩』を《Web立ち読み》しましょう!
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
テトラ「《円》に《楕円》に《双曲線》。おもしろいですねえ……」
後輩のテトラちゃんは、僕の話にしみじみとそう言った。
ここは高校の図書室。いまは放課後。
僕は彼女に《格子点の世界》の話をしていた。
平面上に描いたマス目の線に沿って歩む歩数を《距離》と定義して、 一点からの距離が一定になる図形を《円》と呼び(第411回参照)、 異なる二点からの距離の和が一定になる図形を《楕円》と呼び(第412回参照)、 異なる二点からの距離の差が一定になる図形を《双曲線》と呼んでいたのだ(第413回参照)。
《格子点の世界》で半径が $3$ 歩の《円》

僕「おもしろいよね! 《円》が菱形になるくらいは予想が付いたし、 《楕円》もまあまあわかる。でも《双曲線》は予想を大きく外してきた感じがするよ」
テトラ「確かにそうですね。 あたしが感じたのは『数学用語の理解が試される』ということでした」
僕「へえ。それはどういう意味?」
テトラ「はい。『円』という形はよくわかっています。 こう……ぷわんと丸い形です」
ぷわん、と言いながらテトラちゃんは両手で丸い形を作る。
僕「うん」
テトラ「でも数学では『平面上にあって、ある一点から等距離にある点全体の集合』が円の定義になります。 先輩のおっしゃる《格子点の世界》での《円》を考えるときには『ぷわんと丸い形』というのは手がかりにならなくて、 『一点から等距離にある』という部分が手がかりになる——つまり、 円という用語の定義を理解しているかどうかが試される——と、そんなふうに思ったんです」
円とは『平面上にあって、ある一点から等距離にある点全体の集合』である
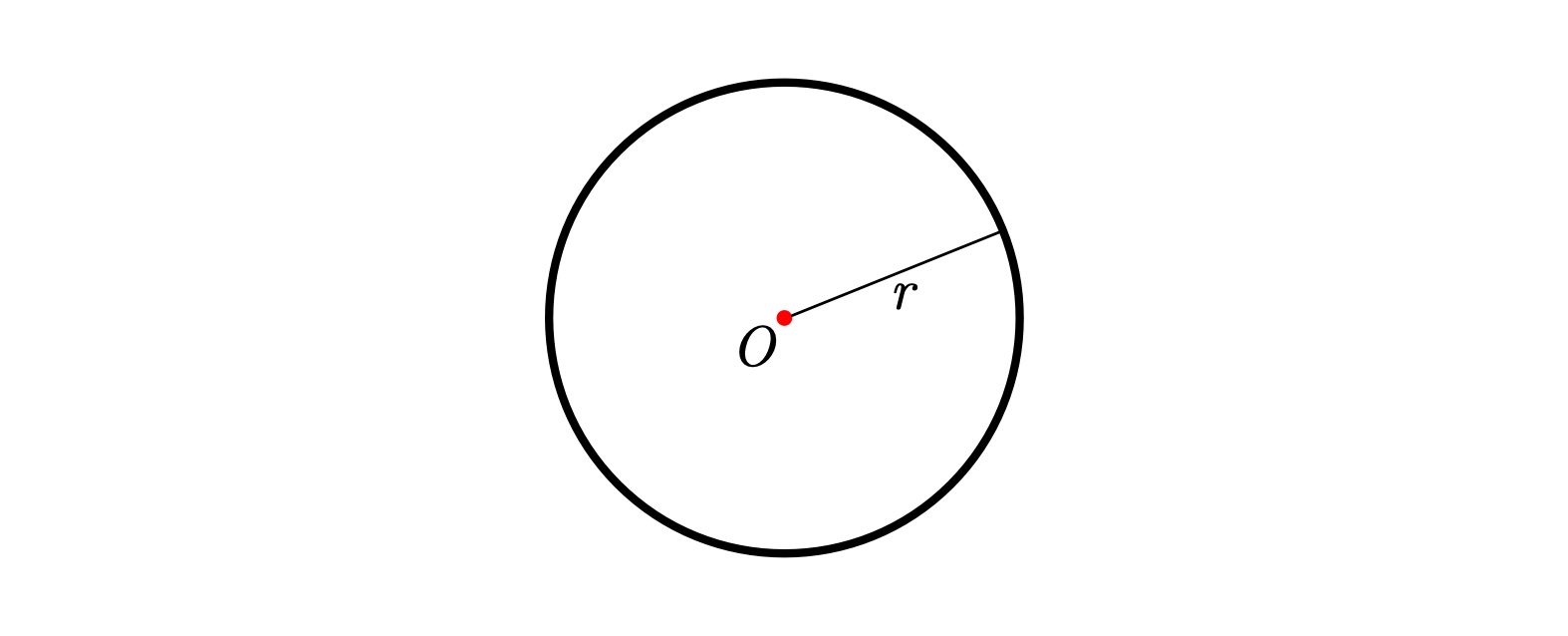
※ここでは点 $O$ から距離 $r$ にある点全体の集合として円が描かれています。
僕「そう! 僕もそれはつくづく思ったよ。 たとえていえば、 《距離》というパスポートを持って《格子点の世界》に行くんだね」
テトラ「他にも思ったことがあります」
僕「なになに?」
テトラ「これも先輩がおっしゃったことですけれど《格子点の世界》に向きがあるという話です。 左右や上下に続けて進むときと、 ジグザグに進むときでは歩数が同じでも距離が——通常の意味の距離が——変わります(第414回参照)。 それが世界の向きに相当しているというお話をおもしろく感じました」
僕「うんうん」
テトラ「そのお話のときにあたしが思い出したのはヘクスマップでした」
僕「ヘクスマップって何?」
テトラ「ボードゲームでよく使われる盤面の形です。 盤面に駒を配置したり、自分の陣地や領地を定めたりする戦略ゲームで、 一つのマス目が正方形ではなく正六角形になっているタイプの盤面が、 ヘクスマップです。いろんな名前がありますけど、 ヘクスというのはたぶんhexagonから来ているんだと思います」
ヘクスマップ

僕「なるほど。正六角形で平面を敷き詰めるタイプの地図なんだ」
テトラ「ですです。《ヘクスマップの世界》では《格子点の世界》と違っていて、 $6$ 方向に $1$ 歩を進めることができます」
ヘクスマップで $1$ 歩進む

僕「そうなるね。《ヘクスマップの世界》での《円》は正六角形ってことになるね!」
なるほど。四方向に動けるよりも六方向に動ける盤面の方が、 通常の《平面の世界》に近い動き方になるってことなのかな。
テトラ「はい、そうなります。 しかもですよ。 $2$ 歩進んだとき、平面上での距離が等しくなるんです!」
ヘクスマップで $2$ 歩進む(A)

僕「確かに……いや、それはおかしいよね。 (A)のように毎回曲がればそうかもしれないけど、 (B)のように、まっすぐ $2$ 歩進んだ場合には平面上の距離は異なるはずだよ」
ヘクスマップで $2$ 歩進む(B)

テトラ「あっ……確かに、ちょっと浅はかでした」
僕「いや、でもともかく、ヘクスマップではまた違う世界が広がることになるね」
ヘクスマップでの《円》は正六角形になりそうだ。 《楕円》はどうなるだろう。そして《双曲線》は……?
テトラ「《ヘクスマップの世界》は《格子点の世界》と違うと思ったんですが、 確かに $2$ 歩進むと曲がりますね……うっかりです」
僕「そうだね。いろんな種類の《線分》が出てくることになる。 《格子点の世界》で図形をたくさん描いたときもそれは感じてたよ。 《平面の世界》だと二点間を結ぶ線分は一本しかないけど、 《格子点の世界》だと二点間を結ぶ《線分》はたくさんある」
テトラ「はい……」
僕「二点が縦横にまっすぐ並んだ場合には《線分》は一本だけど、 斜めになると《線分》は複数本ある。たとえば、 $PQ$ を結ぶ《線分》は一本だけど、 $AB$ を結ぶ《線分》は二本ある。二本とも $2$ 歩の《距離》がある」
二点を結ぶ《線分》
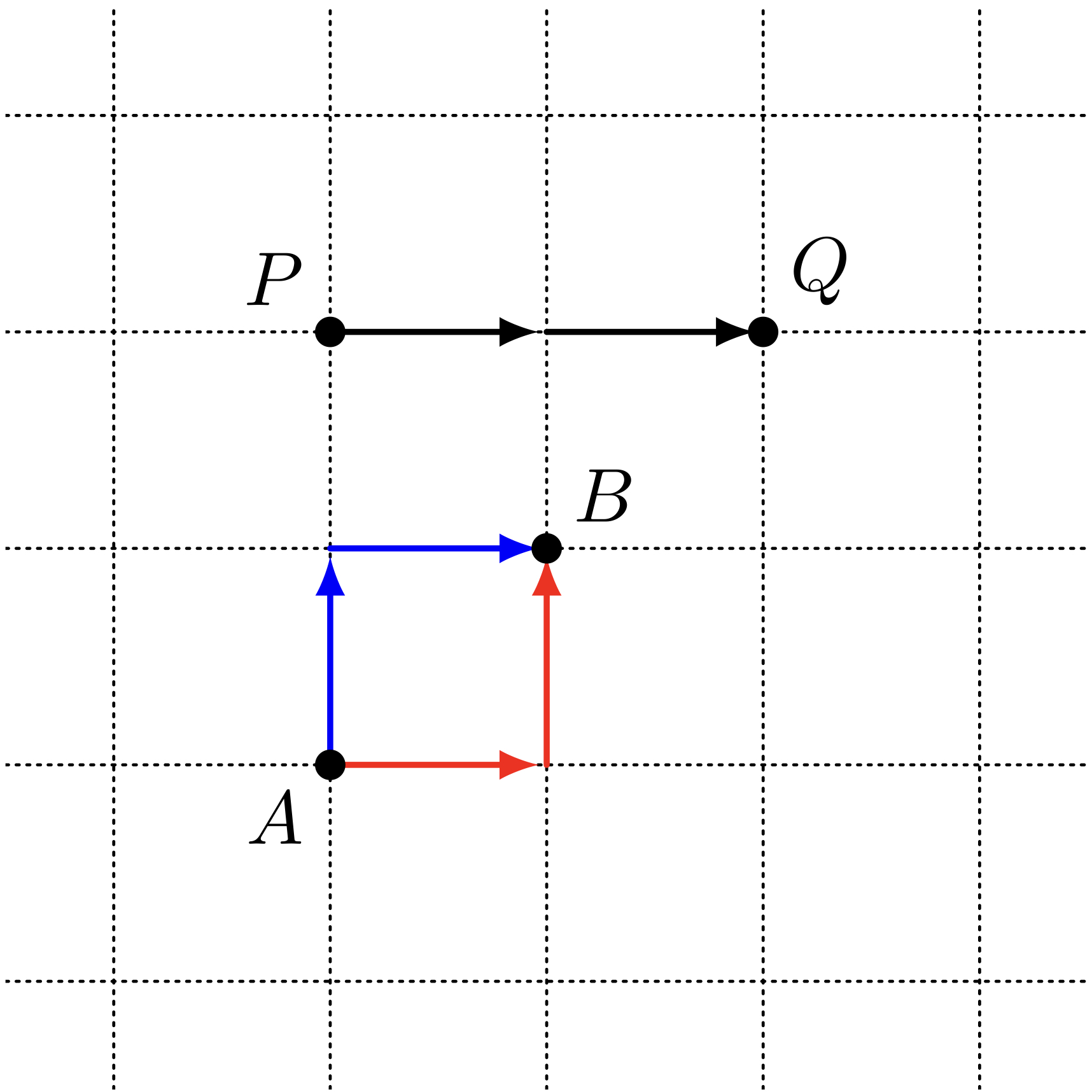
テトラ「斜めの場合、二点が離れれば離れるほど、 《線分》の数は多くなりますよね。 パスカルの三角形や組み合わせの数でよく出てくる図になります。 スタート地点 $S$ からゴール地点 $G$ まで何通りの道があるでしょうか?という問題です」
何通りの道があるか?
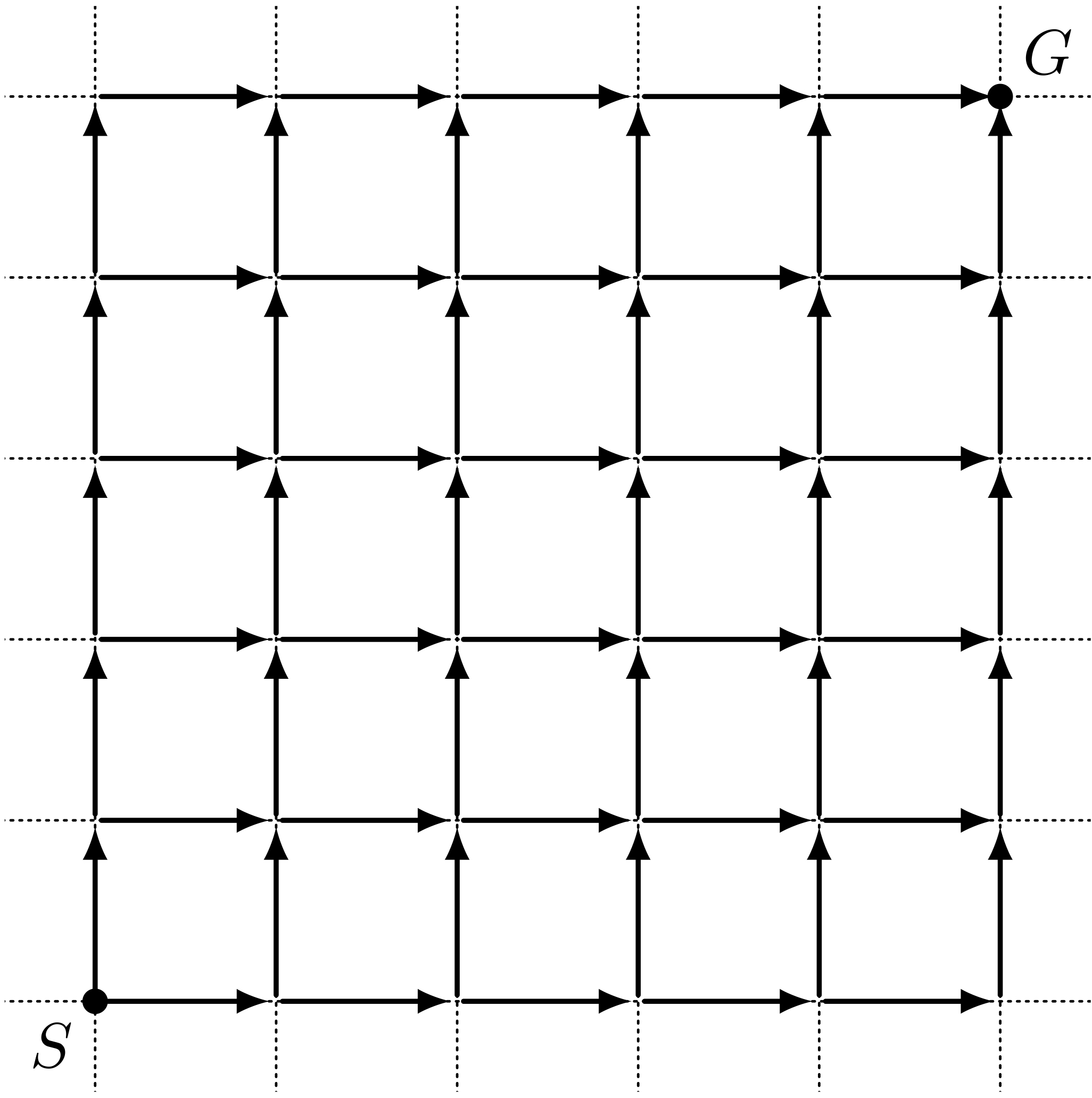
僕「確かにそうだね。 二点を結ぶ《線分》がたくさん生まれてしまうのは、 《格子点の世界》での《線分》を、《距離》だけで決めているから、 といえるかな」
テトラ「《距離》だけで決めている——というのは?」
僕「さっきテトラちゃんが言った『数学用語の理解が試される』と同じだよ。 《格子点の世界》での《線分》は、二点を結ぶまっすぐな線として考えたわけじゃなくて、 二点を結ぶ《距離》が最短の線と考えたから。 だから、二点を結ぶ《線分》は一つに限らないことになった。 世界が変わるときには、用語の定義を再確認することになるんだね」
テトラ「なるほどです。 言葉遊びになるのかもしれませんけれど、 《格子点の世界》に入るときには『円はまるい』や『線分はまっすぐ』という考えを 《平面の世界》に置いていく必要があるわけですね。そして『二点間を結ぶ線分は一本』も捨てたことになります」
テトラちゃんはそう言いながら、大きな荷物を背中から降ろすジェスチャをした。
僕「そう言ってもいいし、 《格子点の世界》では《まるい》や《まっすぐ》が再定義されていると言えるかも。 だって実際、僕たちの世界でも、寄り道したりせずに最短でたどり着くことを《まっすぐ》来たって言うよね。 それこそ言葉遊びになってしまうかもしれないけれどね」
テトラ「まっすぐ……」
そこでテトラちゃんは何かを思い出すように遠い目をした。
彼女の大きな目は何を見ているんだろう。
僕「……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年2月9日)