![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕たちは、ユーリが持ち込んできた《格子点の世界》において《一点からの距離が一定》になる図形、 すなわち《円》を議論していた(第411回参照)。
次に、《異なる二点からの距離の和が一定》になる図形として楕円を思い出し、 試行錯誤しながら、僕たちはなんとか《格子点の世界》における《楕円》を描くことができた(第412回参照)。
そして、さらにそこから《異なる二点からの距離の差が一定》になる図形として双曲線を描こうとした(第413回参照)。
でも、描かれたものは——
僕「……あれ?」
ユーリ「やばい。曲がんないじゃん!」
$\ABS{a-b}=2$ の《双曲線》は二つの《直線》になっちゃった!
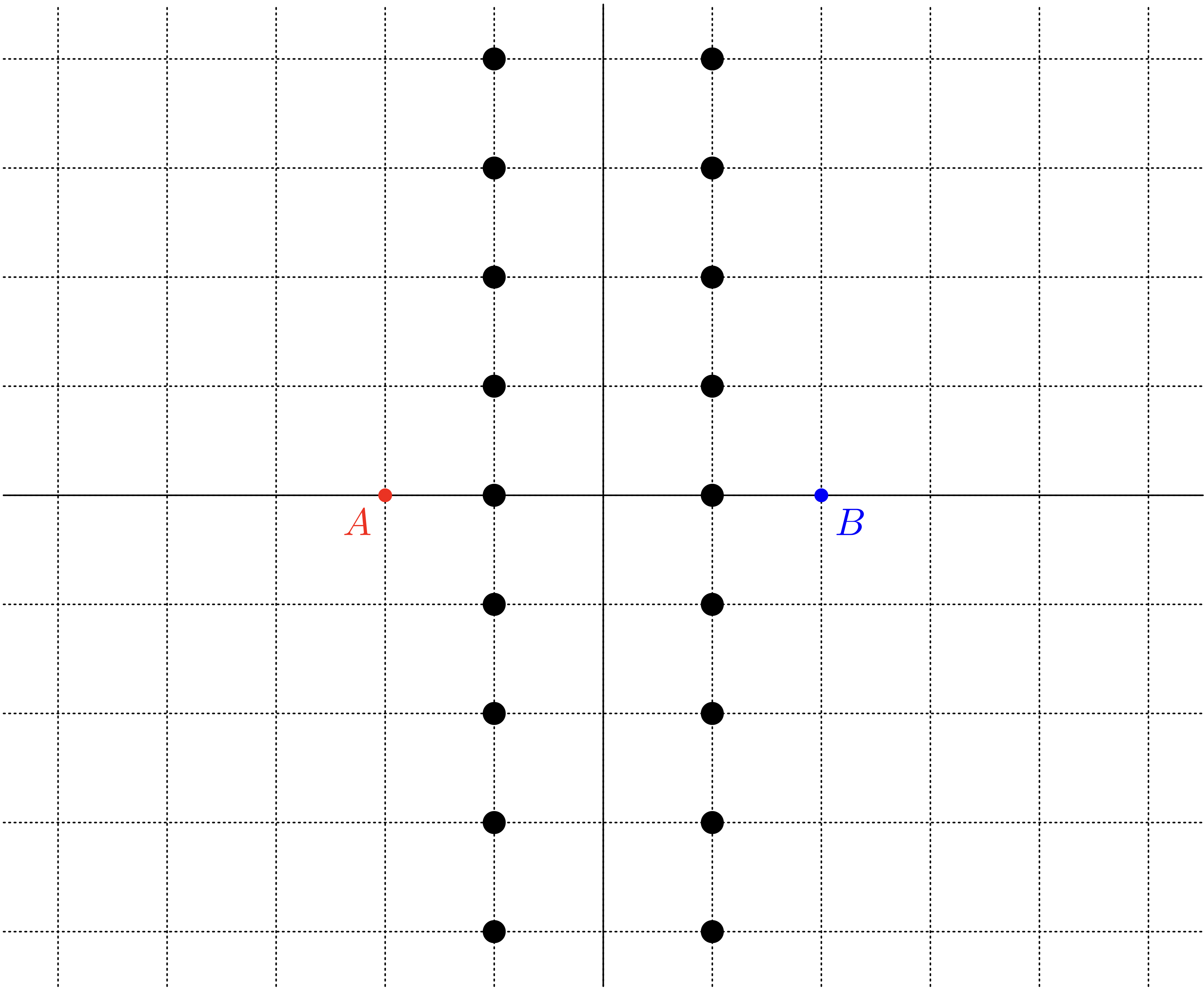
僕「これは……予想外だなあ」
ユーリ「ぜんっぜん、《双曲線》っぽくないね」
僕「そうだなあ……強いて言えば、二本の線になっていて、 無限に続いているところは《平面の世界》の双曲線に似てるといえなくはないけどね」
《平面の世界》の双曲線

ユーリ「むー」
僕「縦軸を対称軸にして左右で線対称になっていて、 横軸を対称軸にして上下で線対称になっているところも似てる」
ユーリ「でも……なんかつまんないにゃあ」
僕「《平面の世界》と《格子点の世界》は違うんだから、違いが出ること自体はしょうがないよ」
ユーリ「……」
ユーリは、僕の言葉にはもう無反応になっていた。
めちゃめちゃ真剣に何かを考えてる。
僕「……」
ユーリは無言のまま、何かを描き始めた。
やがて、満面の笑みを浮かべて、僕に紙を見せる。
ユーリ「お兄ちゃん。ほら見てっ! これなら《双曲線》ぽくない?」
僕「おおお……これは!」
僕は驚いた。
こんなふうに描けば、確かに《双曲線》の面影がある!
ユーリ「$A$ と $B$ を斜めに置いてみたんだよん。うまくいったぜ!」
《格子点の世界》の《双曲線》

僕「なるほど……」
ユーリ「双曲線ってこーゆー配置でもともと覚えてたもん」
《平面の世界》の双曲線
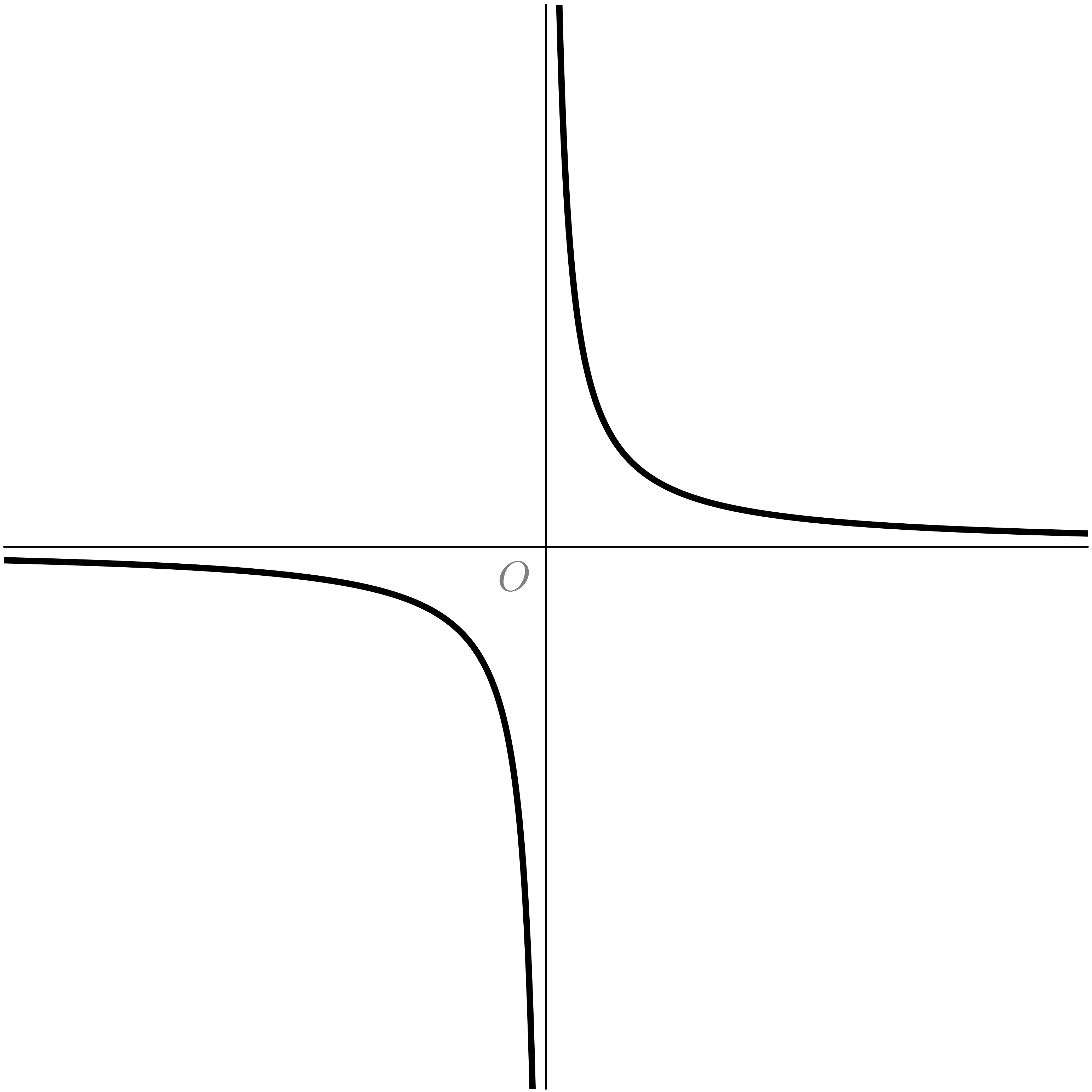
僕「確かに。 $y = 1/x$ はこういう形になるね。 おもしろいなあ! 《平面の世界》の双曲線は横軸と縦軸が漸近線になって、 曲線が限りなくそこに近づいていくけど、 ユーリが描いてくれた《格子点の世界》の《双曲線》はいきなり横軸と縦軸に重なっちゃうんだね」
ユーリ「デジタルっぽくね?」
僕「ところで……これは本当なのかな」
ユーリ「お? 疑いますかね、ダンナ」
僕「誰が旦那だよ。いや、ユーリは二つの《円》の共有点をちゃんと確かめたとは思ってるよ」
ユーリ「たとえばね、 $a=6,b=2$ で二つの《円》を描いたら、 こんなふうにベタッと $3$ 個の共有点ができるよ」
二つの《円》$a=6,b=2$ の共有点は $3$ 個ある

僕「確かにそうか。《格子点の世界》の《円》は菱形になってるから、 二点 $A$ と $B$ を $45$ 度傾けた配置にすると、菱形の辺同士がべったりと点を共有するんだなあ……いわば《接する》わけだ」
二つの《円》$a=6$ と $b=2$ とが《接する》様子
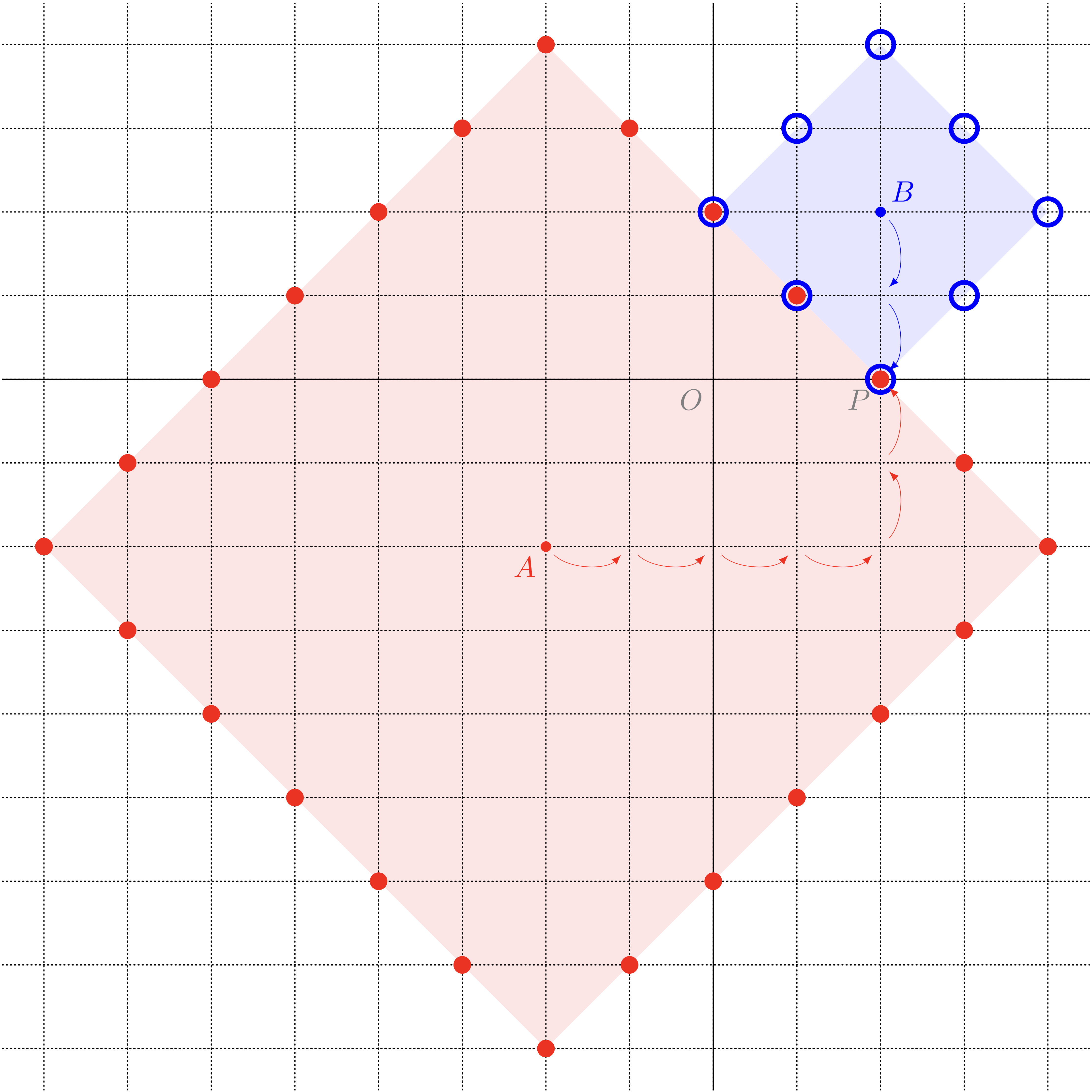
ユーリ「$3$ 点で《接する》っておもしろ! また笑いそう(第413回参照)」
僕「$A$ から $B$ まで $8$ 歩で行けるジグザグな経路と《円周》との共有点が $3$ 個あるってことなんだなあ」
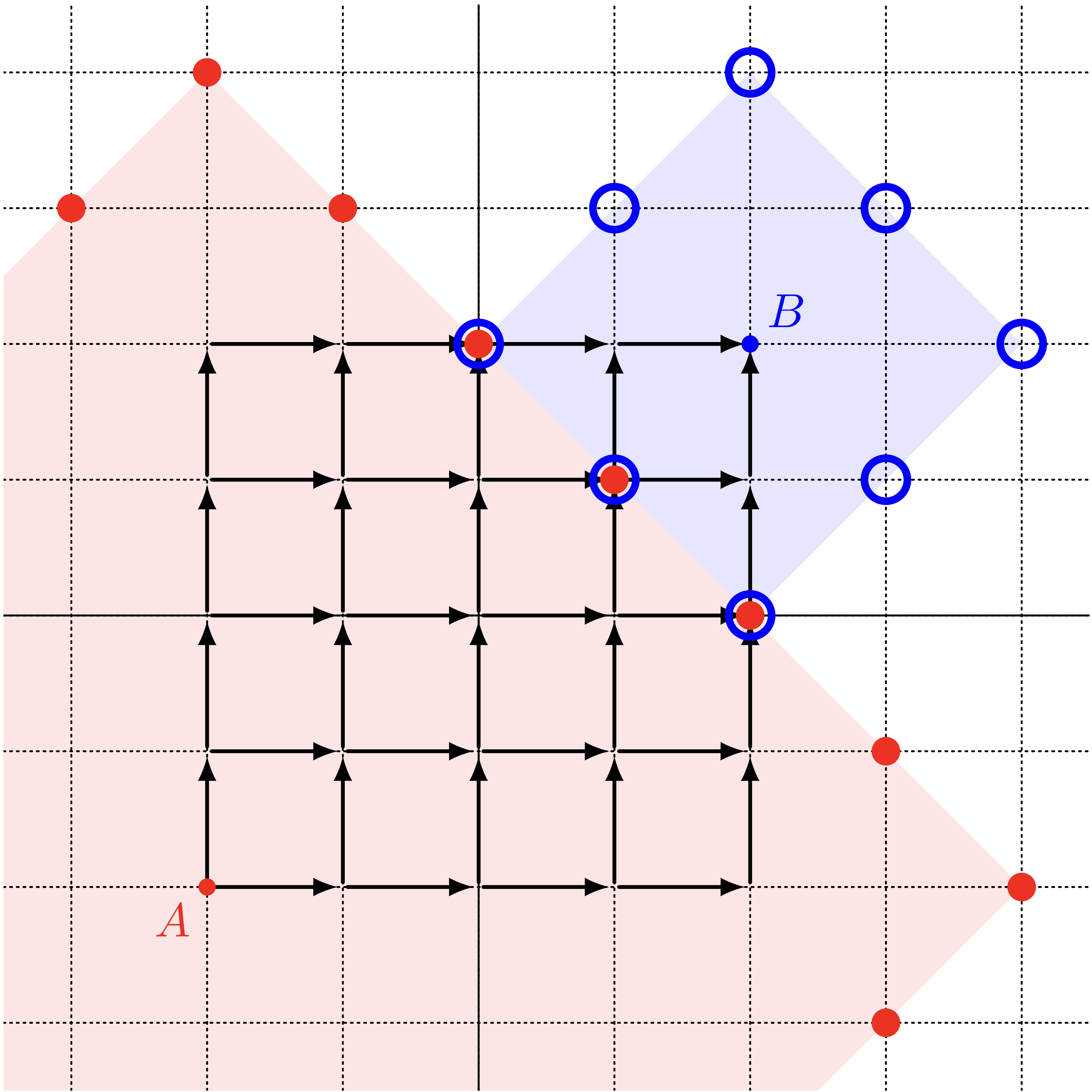
ユーリ「えーとそれから、差が一定で $\ABS{a-b}=4$ なんだから、 $a$ を $6$ から $7$ に増やして、 $b$ を $2$ から $3$ にすればいい。 両方とも《半径》を $1$ だけ大きくして $a=7,b=3$ にすると、二つの《円》の共有点は今度は $2$ 個になるよ。 たとえばこの点 $Q$ はちゃーんと $A$ から $a=7$ 歩、 $B$ から $b=3$ 歩になってるっしょ?」
二つの《円》$a=7,b=3$ の共有点は $2$ 個ある
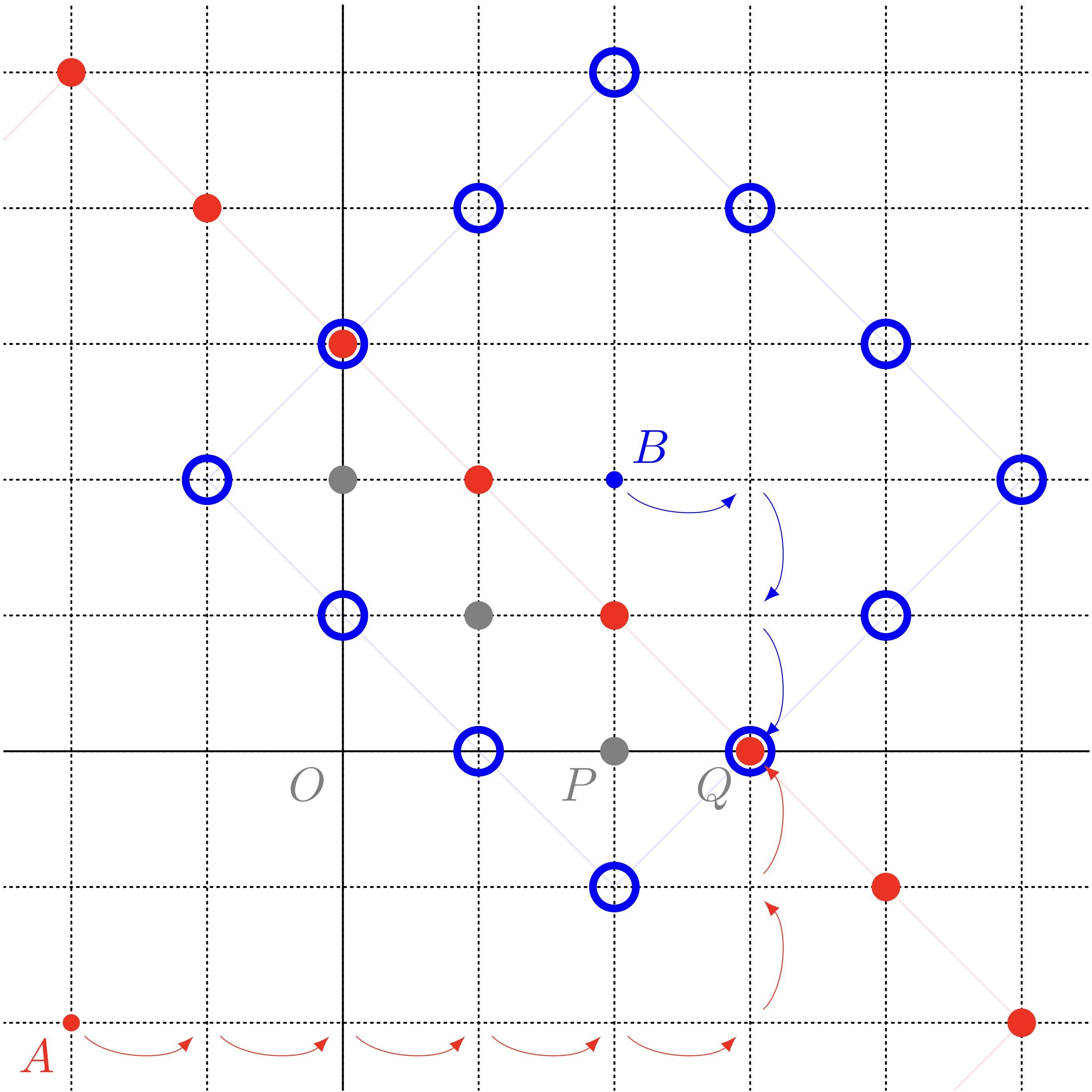
※ $a=6,b=2$ で見つかった $3$ 点はグレーにしています。
僕「うん、それはわかるな。 そして、そこから二つの《円》の《半径》を大きくしていくと、 交点は軸の上を原点から離れる向きに進むわけだね」
$A$ と $B$ を斜めに配置した《格子点の世界》の《双曲線》
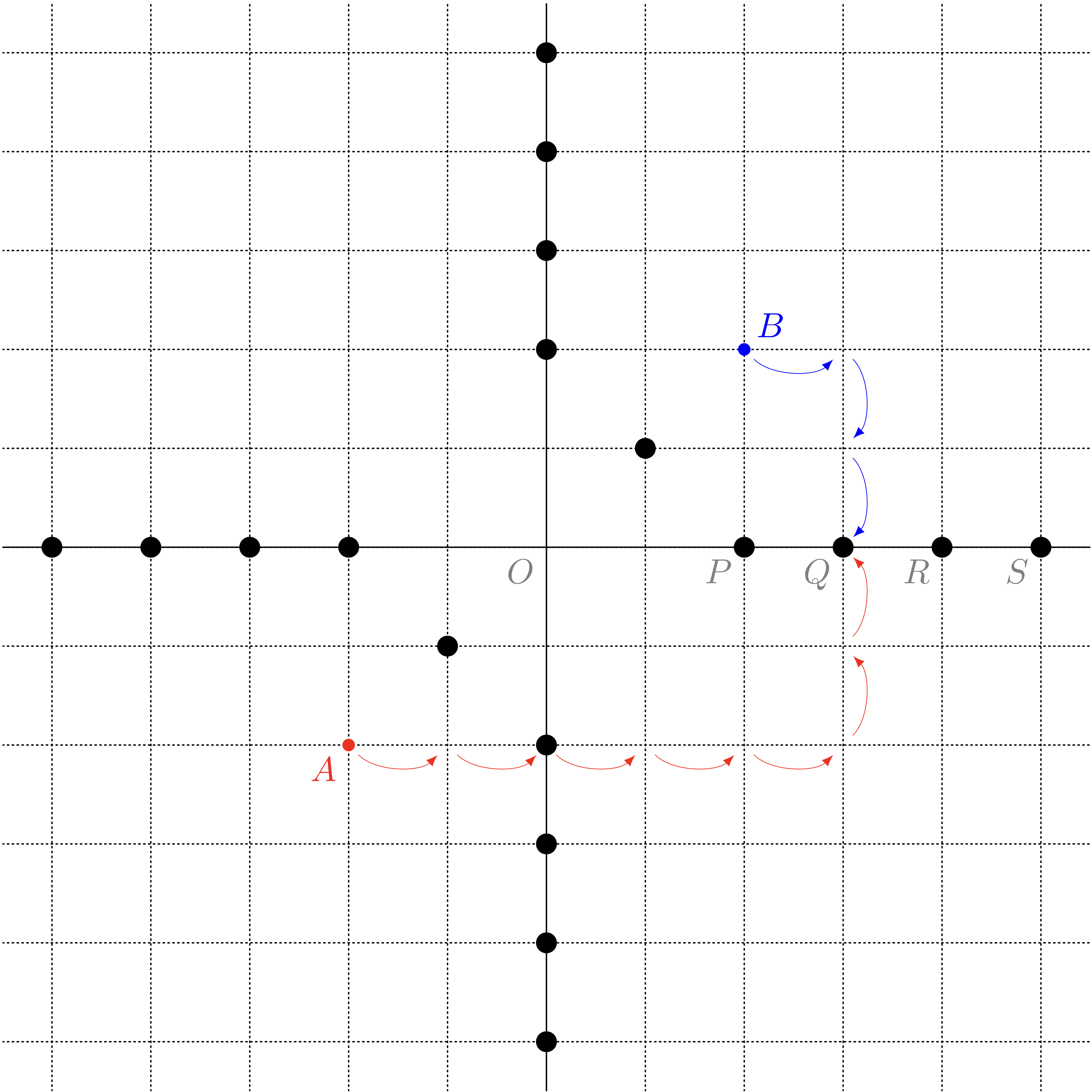
ユーリ「そーそー。 $a$ と $b$ をどっちも $1$ ずつ増やしていけば $\ABS{a-b}$ の値はずっと変わらないから、 $$ P \to Q \to R \to S \to \cdots $$ のみたいに無限に続いてく。《双曲線》誕生なり〜」
僕「うーん。確かにこうなるなあ」
ユーリ「ふふん。《格子点の世界》でも《異なる $2$ 点からの差が一定》で曲がった線——曲がった点の列——ができた」
僕「それは、どうしてだろう?」
ユーリ「え。まだ疑ってんの? ちゃーんと二つの《円》描いたっしょ?」
僕「いやいや、疑っているわけじゃない。全然違う。 そうじゃなくて、 《格子点の世界》の《双曲線》が曲がるときと曲がらないときがある理由を考えてただけだよ」
《格子点の世界》の《双曲線》は曲がるときと曲がらないときがある
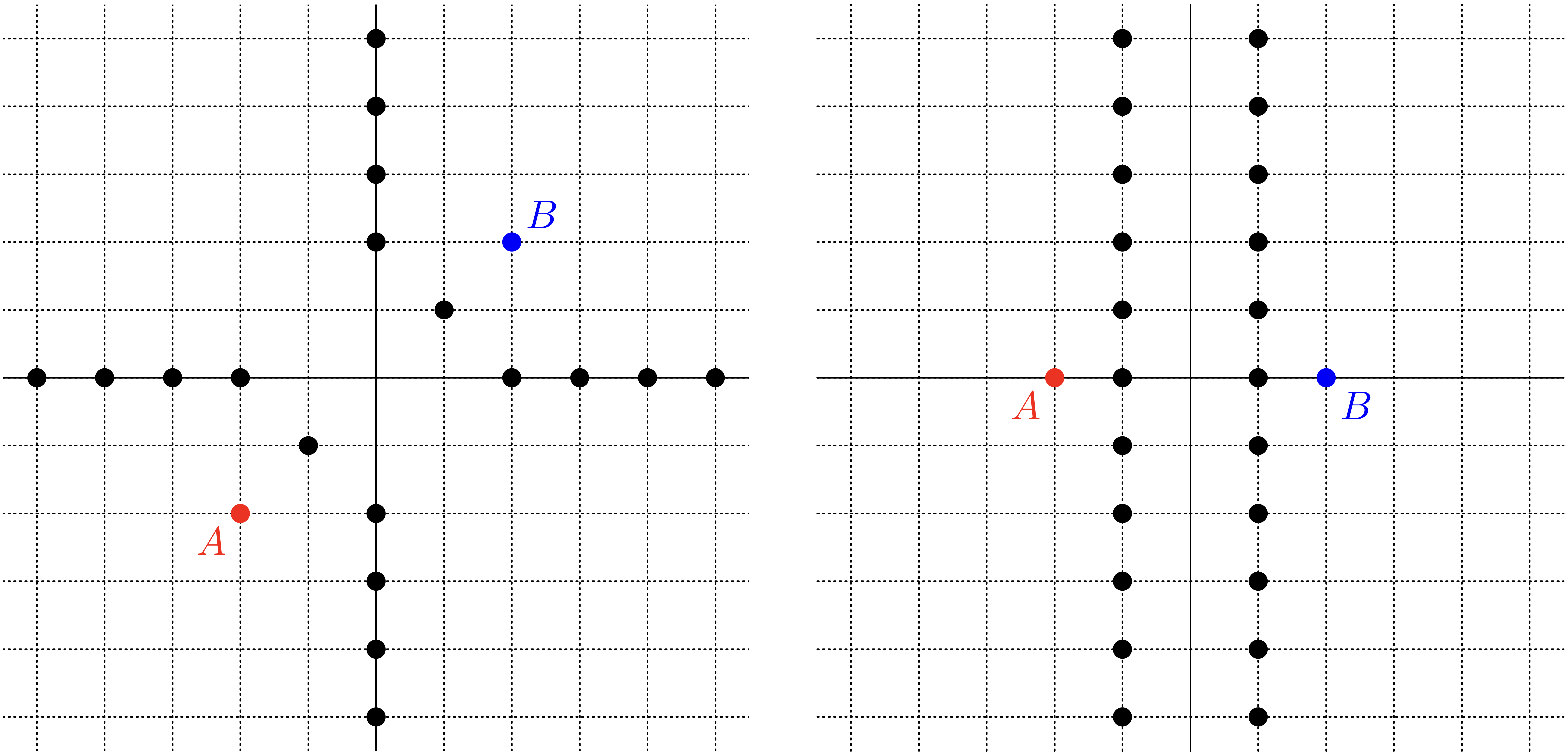
ユーリ「理由?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年2月2日)