![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
【CM】今シーズンの話題は『数学ガールの秘密ノート/場合の数』でも詳しく読むことができます。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
テトラ「おもしろいですねえ……」
テトラちゃんは、うなずきながらしみじみとそう言った。
ここは高校の図書室。いまは放課後。
僕はテトラちゃんに、先日のユーリとのおしゃべりを伝えていた(第391回参照)。
パスカルの三角形と組み合わせの数の話だ(第394回参照)。
僕「パスカルの三角形はおもしろいよね。 二つの数を足し合わせて進むだけで、組み合わせの数がぞくぞく生まれてくるんだから」
パスカルの三角形は行ごとに作っていく。
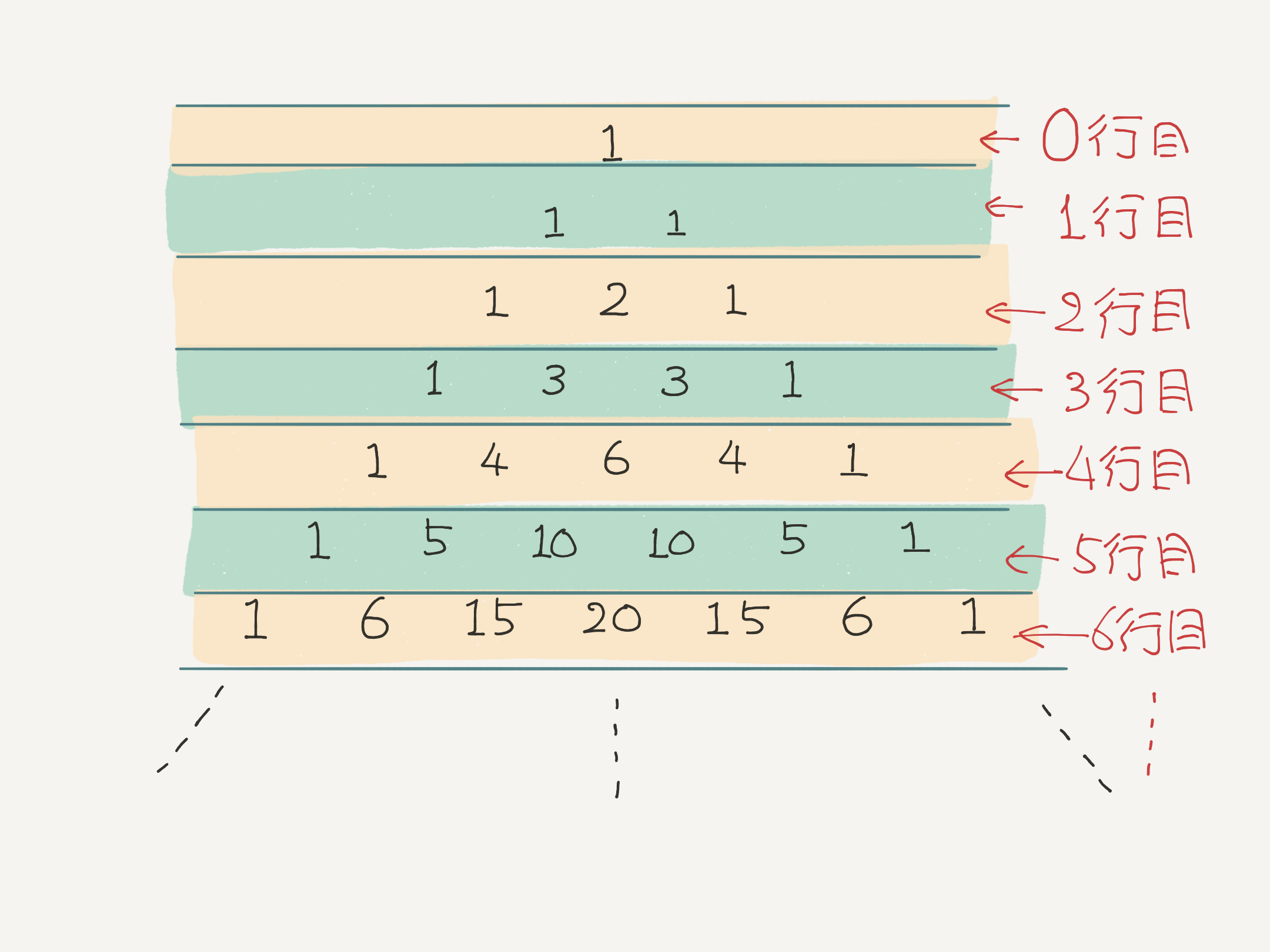
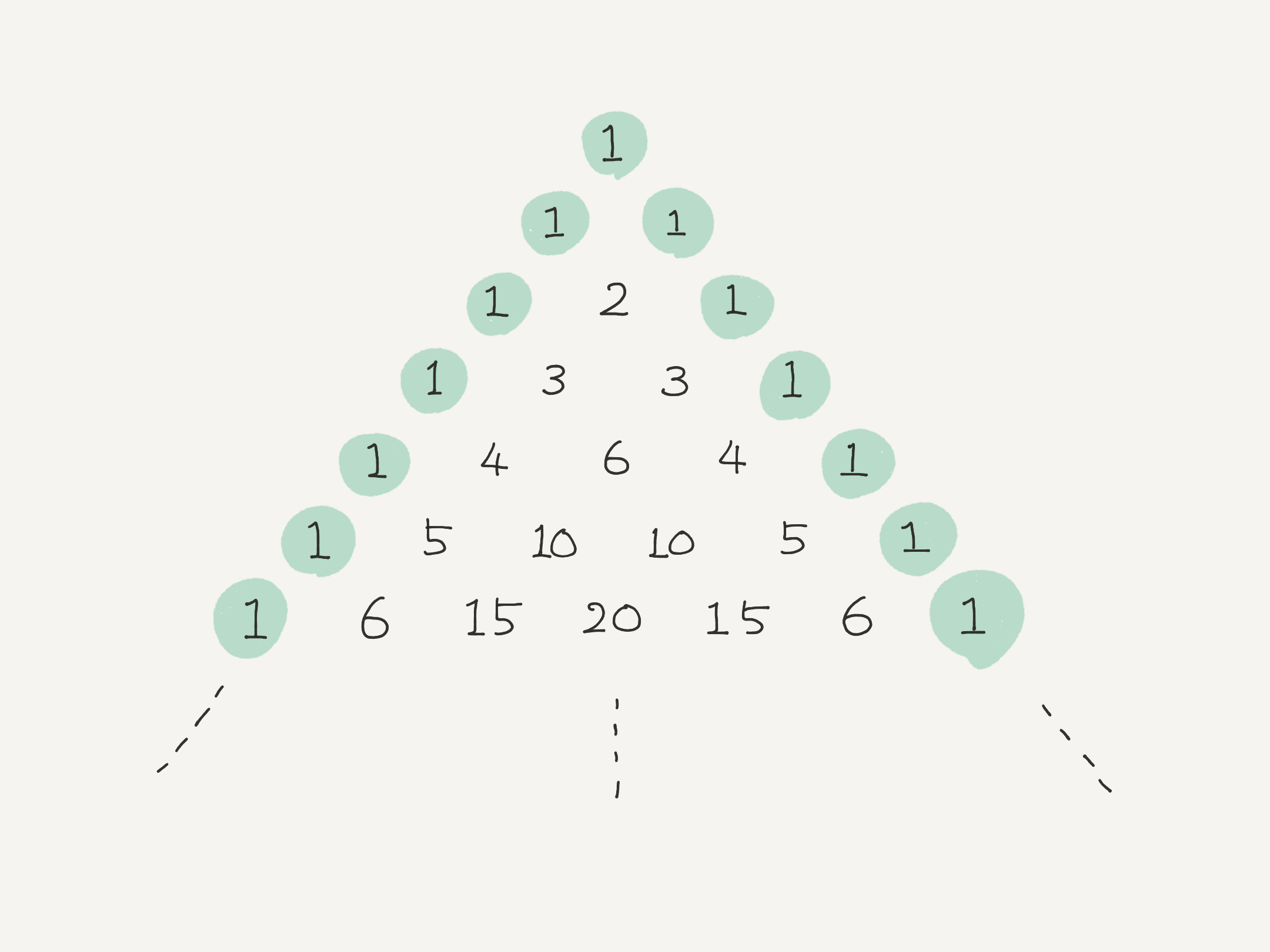
両端の数は、 $1$ にする。
両端以外の数は、ちょうど上に並んだ二つの数を足し合わせた結果にする。
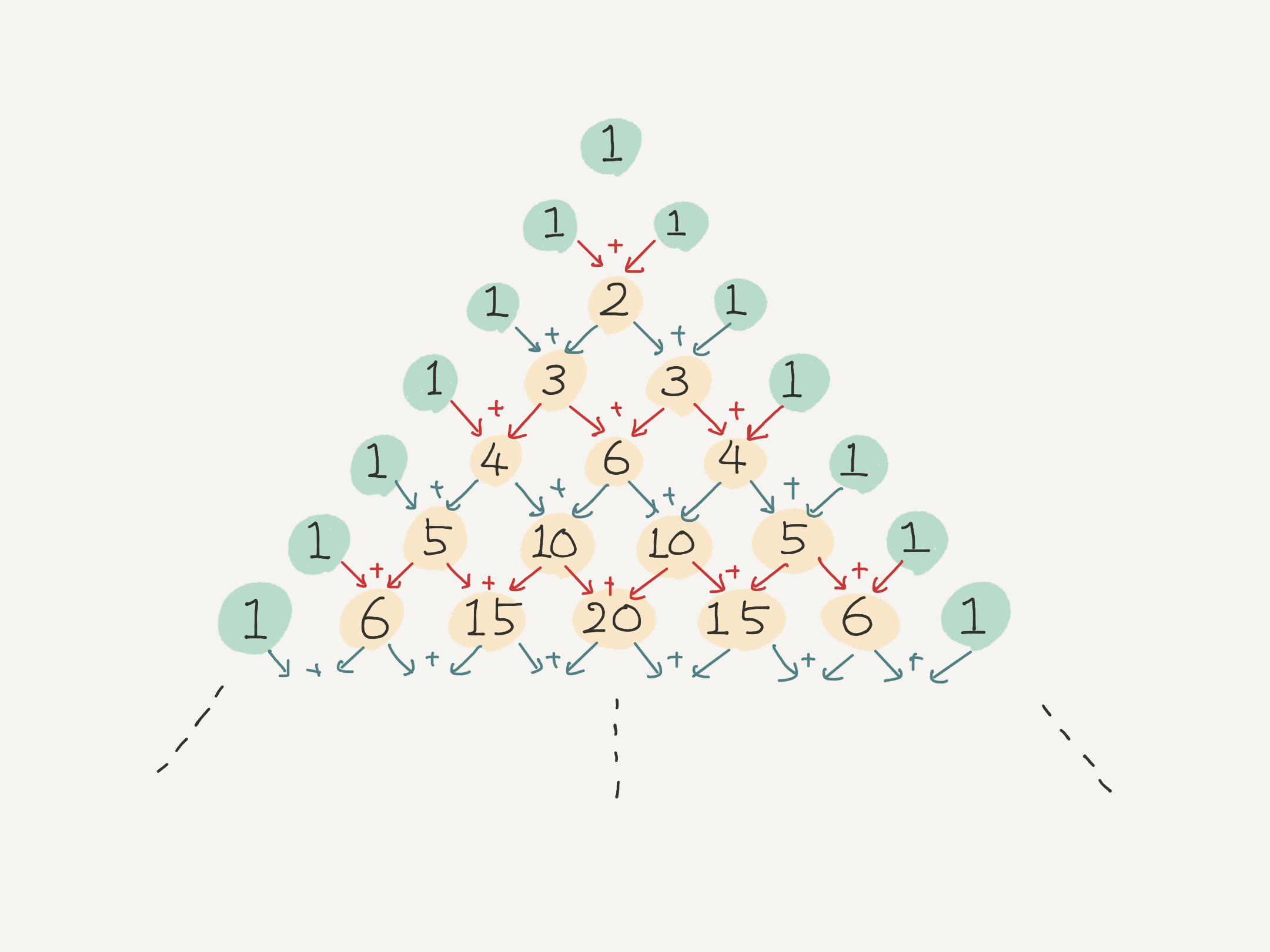
パスカルの三角形を書いていく様子(YouTube)
テトラ「あっ、いえっ、そうなんですけど、そうじゃなくて——」
テトラちゃんは両手をバタバタさせて一人でなぜか混乱している。
テトラちゃんは僕の後輩。
放課後にはいつも図書室で数学のおしゃべりをする仲間なのだ。
僕「どういうこと?」
テトラ「あたしが『おもしろい』と思ったのは、 ユーリちゃんの目の付け所です。着眼点、ですね。 パスカルの三角形では《足し算》しか出てこないのに、 組み合わせの数なんていう複雑なものが出てくるのはなぜか——その着眼点がすごいと思いました」
僕「なるほど、それは確かにそうだなあ。 《足し算》だけに注目するんじゃなくて《何と何を足しているのか》に注目すると、 謎が解けていくんだけどね(第392回参照)」
テトラ「はい。パスカルの三角形の上の頂点から降りてくる道筋の数に注目するわけですね」
僕「そういう話。ユーリとはパスカルの三角形の話に終始したけど、 《何と何を足しているのか》に注目するというのは漸化式に注目していることに なるんだ」
テトラ「ぜんかしき……?」
僕「うん、そうだよ。 $n$ 個のものから $r$ 個を選ぶ組み合わせの数を、$$\BINOM n r$$で表したとき、 その $\TBINOM n r$ が満たす漸化式はパスカルの三角形の作り方そのもの」
テトラ「ちょ……ちょっとすぐにはピンと来ません。何となくはわかるんですけれど」
僕「うん、入り組んでいてちょっとややこしいけれど、難しい話じゃないよ。 きちんと書いてみるね」
テトラ「はい!」
僕「まず、 $n$ 個のものから $r$ 個を選ぶ組み合わせの数を $\TBINOM n r$ で表すというのはいいよね。 $n$ と $r$ はどちらも $0$ 以上の整数とする」
組み合わせの数
$n$ 個のものから $r$ 個を選ぶ組み合わせの数を、 $$ \BINOM n r $$ で表すことにする。 これは、 $$ \COMBI n r $$ と書くこともある。
テトラ「はい。これはわかります。 たとえば、 $n = 4$ で $r = 3$ として考えると、 $4$ 個のものから $3$ 個を選ぶ組み合わせの数は $4$ ですから、 $$ \BINOM 4 3 = 4 $$ ということですよね」
僕「そうそう。即座に《小さい数で試してみる》なんて、さすがテトラちゃんだね」
テトラ「き、恐縮です。 あ、でもいまの $n = 4$ と $r = 3$ というのは簡単すぎましたね。 だってどの $3$ 個を選ぶかというのは、どの $1$ 個を選ばないかですから、 $4$ 通りだとすぐにわかります。当たり前です」
僕「まあ、そうだけど、当たり前——」
テトラ「《当たり前のことから始めるのはいいこと》ですねっ!」
僕「スローガンを先取りされてしまった」
テトラ「ふふっ」
僕「$4$ 個のうちから $3$ 個を選ぶ組み合わせの数は、 $4$ 個のうちから $1$ 個を選ぶ組み合わせの数に等しい。 というときに、 $1$ という数が $4-3$ であることに気付けば、 $$ \BINOM{4}{3} = \BINOM{4}{1} $$ というのは、 $$ \BINOM{4}{3} = \BINOM{4}{4-3} $$ を使っていたことになる。その考え方を一般化すると、 $$ \BINOM{n}{r} = \BINOM{n}{n-r} $$ になるのもすぐわかる」
テトラ「はい、わかります。左辺の $\TBINOM{n}{r}$ は $n$ 個から $r$ 個を選ぶ組み合わせの数で、 右辺の $\TBINOM{n}{n-r}$ は $n$ 個から $n-r$ 個を選ぶ組み合わせの数。 この二つは等しい——ということ」
僕「そういうこと。ユーリは何を選ばないかを選ぶと言ってたかな」
テトラ「パスカルの三角形が左右対称になっているのに通じますね。 $r$ を選ぶことと $n-r$ 個を選ぶのはある意味で 同じこと」
僕「そうだね、さすがテトラちゃん!」
テトラ「……確かに、 $\TBINOM{n}{r}$ のような書き方をすると、表現したいことを簡潔に表せます。 本当に、数式は——」
僕「《数式は言葉》だよね!」
テトラ「スローガンを先取りされてしまいましたっ!」
僕とテトラちゃんは笑い合った。
僕「テトラちゃんは $\TBINOM n r$ を階乗を使って書き表すことはできるよね?」
階乗
$n$ を $0$ 以上の整数とする。
$n \GEQ 1$ のとき、 $1$ から $n$ までの整数をすべて掛け合わせたものを $n$ の階乗といい、 $$ n! $$ で表す。すなわち、 $$ n! = 1 \times 2 \times \cdots \times n $$ である。
$n = 0$ のときは、 $n$ の階乗の値は $1$ であると定義する。 $$ 0! = 1 $$
テトラ「え? あ、はい。大丈夫です。 $\TBINOM n r$ を階乗で書き表すというのは、 こういう意味ですよね?」
組み合わせの数を階乗で表す
$n$ 個のものから $r$ 個を選ぶ組み合わせの数 $\TBINOM n r$ は、 次の式で表すことができます。 $$ \BINOM n r = \frac{n!}{r!\SP(n-r)!} $$
僕「そうそう。あ、念のために聞くけど、 $n$ と $r$ の条件は?」
テトラ「はい。 $n$ と $r$ は $0$ 以上の整数です」
僕「……」
テトラ「?」
僕「もう一声!」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2023年6月16日)