第392回 シーズン40 エピソード2

パスカルの三角形（後編）

システマティックに数え上げ

僕「……システマティックっていうのは、『系統立てている』という意味の英語だよ。 行き当たりばったりに書き並べたんじゃないってこと。 英和辞典で英単語がアルファベット順にならんでいるのと同じように、 組み合わせを列挙している」

ユーリ「いやー、全然意識してませんでしたぜ、ダンナ」

僕「誰がダンナだよ。 《$4$ 個のものから $2$ 個を選ぶ組み合わせ》だったら $6$ 通り。 それなら、少ないからあまり間違ったりはしない。 でも、組み合わせの数は、とても多くなるときがある。 だから、列挙していくときには、システマティックに列挙しないとすぐに混乱してしまうんだ。 たとえば、樹形図を使うのも、システマティックに考えるのにいいよね」

ユーリ「樹形図は学校で習ったよ。でもシステマティックって習ってない」

僕「システマティック（systematic）に数えるっていうのは、このあいだテトラちゃんが言ってたことだよ。 根気よく数えるために大事だって話だったかな。テトラちゃんはそういうのが好きなんだね」

ユーリ「テトラさん、言いそう」

僕「システマティックに数えたり、列挙したりする方法は他にもあるよ。たとえば……」

ユーリ「たとえば、表（ひょう）でしょ！？　ユーリ、作れるよ。ほら、こんな表」

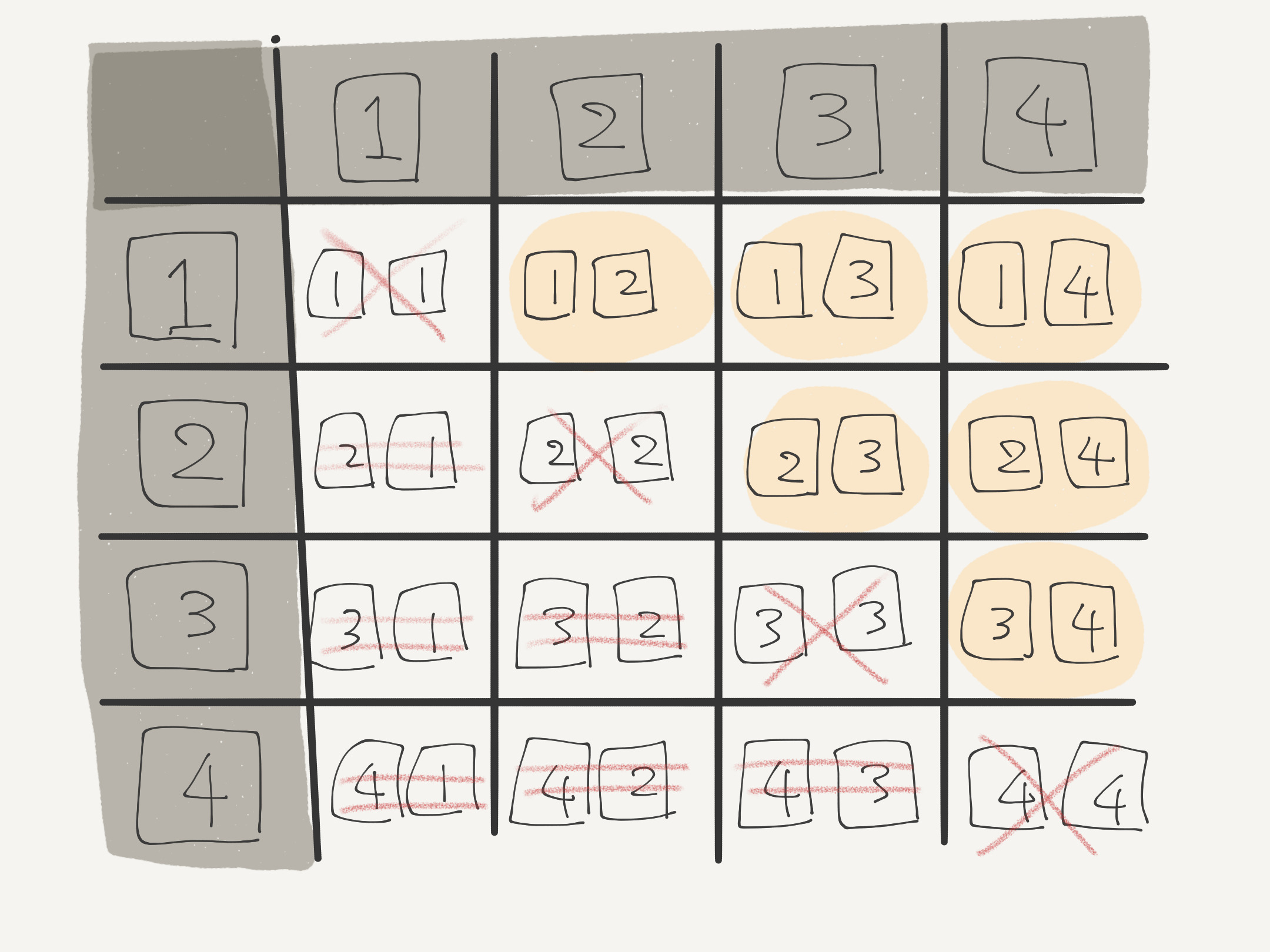
僕「なるほど……ん？」

ユーリ「お兄ちゃん、もちろんわかるよね、この表。 《$4$ 個の数から $2$ 個選ぶ》ときなら、こんなふうに表にすればいーじゃん？　同じ数は選ばないし、 $2,3$ と $3,2$ をだぶって選ぶこともない。 だから、まちがいなく、 $4$ 個から $2$ 個選ぶ組み合わせの数は $6$ 通りだってわかる！」

僕「いや、これはこれで正しいんだけど、 この表は、 $n$ 個の数から $2$ 個選ぶときに限るよね」

ユーリ「え？　あ、ほんとだ！」

僕「$2$ 個選ぶときには、こんなふうに表にするとわかりやすいし、 確かにシステマティックといえる。行き当たりばったりじゃない。 でもたとえば、 $4$ 個の数から $3$ 個選ぶときには使えない。惜しかった」

ユーリ「そっかー。表にすればいいってもんでもないのかー」

パスカルの三角形に戻る

僕「ところで、もともとのユーリの研究に戻ろうか」

ユーリ「ユーリの研究って何だっけ」

僕「がく。パスカルの三角形を作るときには、上の行の二つの数を足して下の行を作ることを繰り返す。 どうしてその作り方で《組み合わせの数》が出てくるのか——だろ？（第391回参照）」

ユーリ「そーだった」

僕「確かに、ユーリが言う通り、パスカルの三角形に出てくる数はすべて、 《$n$ 個のものから $r$ 個のものを選ぶ組み合わせの数》になってる。 三角形の形を、こんな表に変形してみるとわかりやすい」

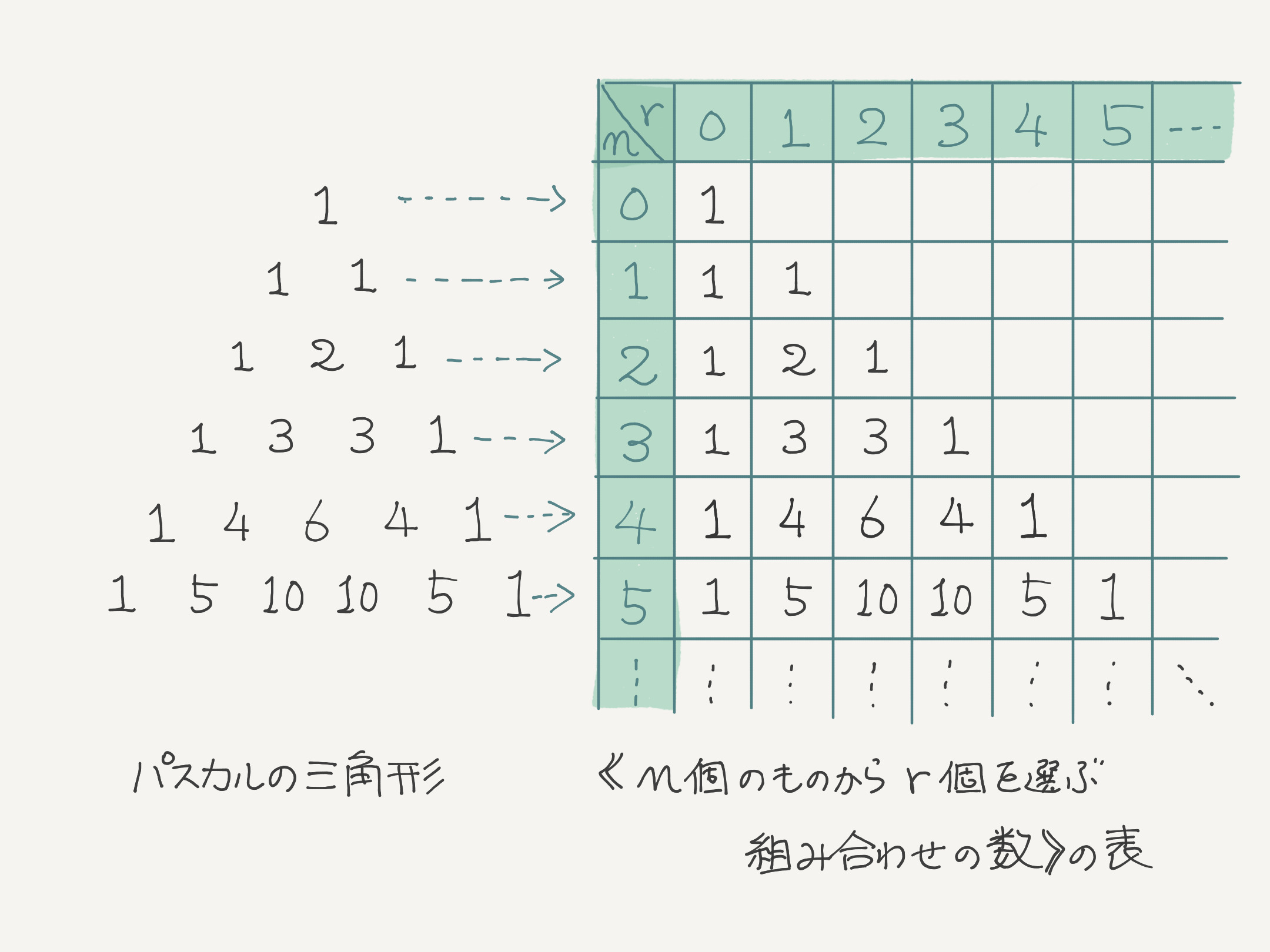
ユーリ「それそれ。不思議じゃん？」

僕「ユーリは不思議だと感じる。じゃあね、どういうところが不思議だと感じるのか、それを教えてほしいな」

ユーリ「そんなの、感覚的な話だもん」

僕「だからその感覚的な話を聞きたいんだけど」

ユーリ「どーゆーところが不思議か。んーとね……」

僕「……」

ユーリ「……あのね、組み合わせの数ってめんどくさいよね。 システマティック（だっけ？）に数えないと間違えるくらいめんどくさい。 でも、二つの数を足すって簡単なことじゃん。そーゆーとこが不思議」

僕「なるほど。それは確かにそうだね。 すべての組み合わせを《もれなく、だぶりなく》数えるのは難しいし、 まちがいやすい。それなのにどうして二つの数を足すだけで組み合わせの数が得られるのか——言われてみればそうだね。 不思議と言えば不思議だ」

ユーリ「そんで？」

僕「二つの数を足すこと自体は簡単だけど、大事なのは何と何を足していることになるかだと思うよ。 パスカルの三角形で、足し算をしているところをじっくり調べてみようか。 特に、三角形の最初のところをズームアップしてみよう！」

ユーリ「おー！」

パスカルの三角形をズームアップ

僕「こんなふうにズームアップしてみたよ」

ユーリ「これ、どゆこと？」

僕「パスカルの三角形の各行の両端は $1$ になる。そして両端以外の数は、上の行の二つの数を足す。 だから最初の足し算は $1+1$ になるよね」

ユーリ「$1+1=2$ だね」

僕「その計算をあえてやらない（・・・・）。つまり $2$ にしないで、 $1+1$ のままにしておくんだ」

ユーリ「ほほー……なんで？」

僕「$1+1$ のうち、左の $1$ は左上から来た数で、右の $1$ は右上から来た数。 $2$ と書いちゃうとわからなくなるけれど、 $1+1$ と書けば、左上と右上の数を足したんだということがわかる」

ユーリ「ふむふむ」

僕「そしてその次の行も同じように、計算しないで式のまま書いておくことにする」

ユーリ「うーん……意味はわかるけど、めんどくさくしてるだけでは？」

僕「そうじゃないんだ。次に、 $1+1$ まで降りてくる《道筋》を考える」

ユーリ「みちすじ？」

$1+1$ まで降りてくる道筋を考える

僕「三角形の一番上にある頂点の $1$ を山のてっぺんだと考えて、 そこから $1+1$ のところまで降りてくる道筋は、こんなふうに $2$ 通りある。 そしてその $2$ という数は、左上の $1$ と右上の $1$ を足した $1+1$ で得られている……と考えてみる」

ユーリ「ふむふむ？」

僕「わかるよね」

ユーリ「わかるけど、当たり前だからおもしろくない」

僕「次になるとちょっとおもしろいよ」

ユーリ「次？」

$1+(1+1)$ まで降りてくる道筋を考える

僕「$1+(1+1)$ まで降りてくる道筋は、こんなふうに $3$ 通りある。 そしてその $3$ という数は、左上の $1$ と右上の $1+1$ を足した $1+(1+1)$ で得られている……よね？」

ユーリ「むむむ……ちょーっと待って！」

僕「待ってるよ」