第378回 シーズン38 エピソード8

「回る」と「回す」（後編）

図書室にて

テトラ「……なるほど。 $s = r\theta$ と $v = r\omega$ の関係がわかりました」

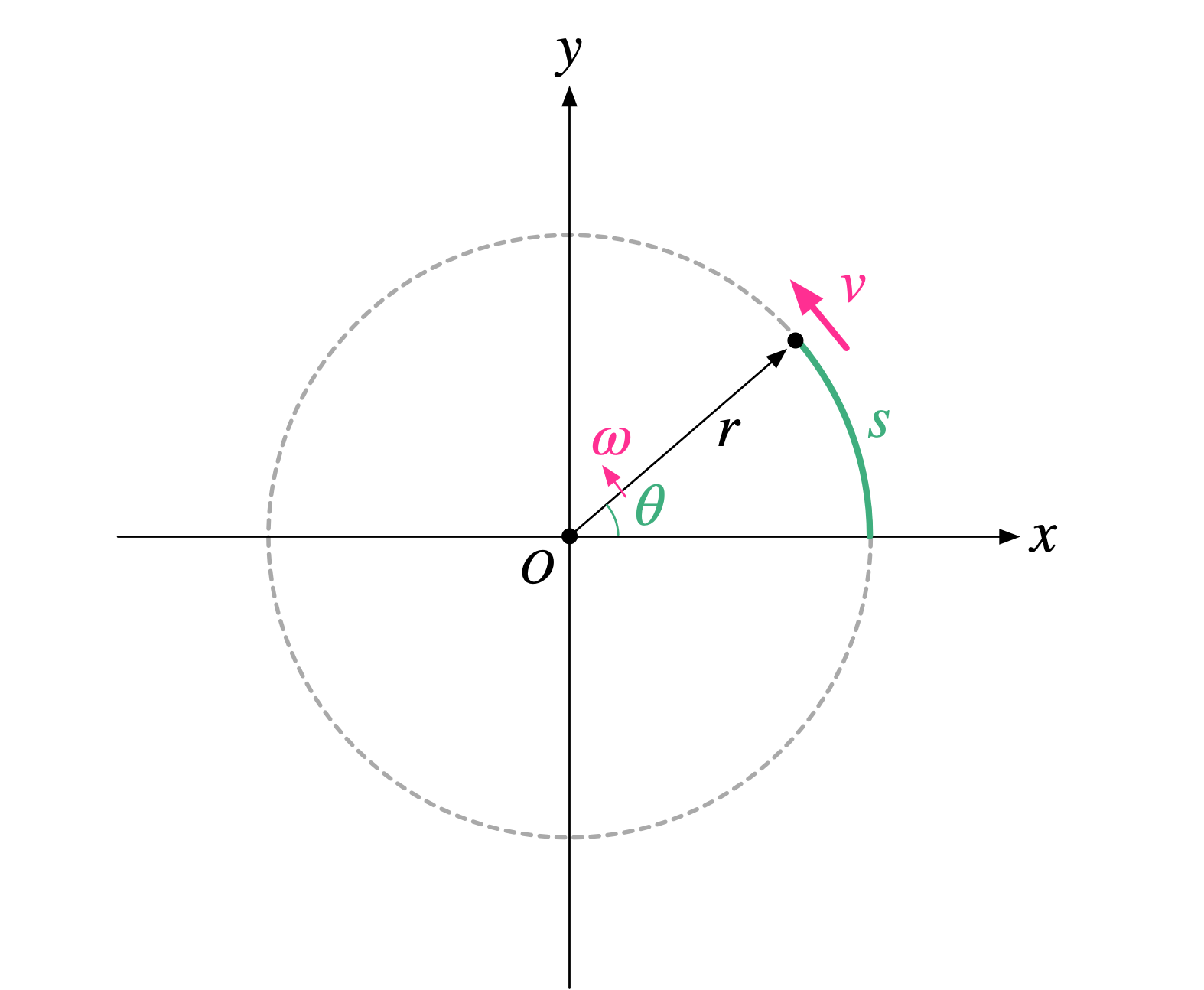
僕「ここまでで、速度の大きさである速さ $v$ と角速度 $\omega$ の関係はわかった。 次に、速度ベクトル $\vec v$ についてどうなるかを考えてみよう」

速度ベクトル $\vec v$

テトラ「速度ベクトル $\vec v$ は、位置ベクトル $\vec x$ を微分する？」

僕「そうそう、位置ベクトル $\vec x$ を時刻 $t$ で微分してみよう。そうすると何が出てくるかというと、もちろん速度ベクトルだね。 速度ベクトルを $\vec v$ で表して、その $x$ 成分を $v_x$ として、 $y$ 成分を $v_y$ としてみる。そして……」

テトラ「ちょっとお待ちください。いま出てきた $v_x,v_y$ というのはそのように名前付けをしたというだけですよね？」

僕「うん、そうだよ」

テトラ「失礼しました」

僕「いやいや、気になるのを確かめるのは大事だよね。 $v_x,v_y$ としてもいいし、たとえば $u,v$ としてもいい……けど、速さを $v$ にしたからそれはまずいか。 ともかく、速度ベクトルは位置ベクトルを時刻 $t$ で微分したものだから、こうなる」

$$ \begin{align*} \vec v &= \frac{d}{dt}\vec x && \REMTEXT{速度ベクトルは位置ベクトルを時刻で微分したもの} \\ &= \frac{d}{dt}\VECV{x}{y} && \REMTEXT{位置ベクトルを成分で表現した} \\ &= \VECV{\frac{d}{dt}x}{\frac{d}{dt}y} && \REMTEXT{成分ごとに微分した} \\ \VECV{v_x}{v_y} &= \VECV{\frac{d}{dt}x}{\frac{d}{dt}y} && \REMTEXT{つまり、この式が成り立つ} \\ \end{align*} $$

テトラ「ええと……これはまだ話は進んでいないですよね？　つまり、 これは《速度ベクトルは位置ベクトルを時刻で微分したものですよ》と、 《ベクトルを微分するときには成分を微分すればいいんですよ》というお話ですよね？　ね、念のための確認です」

僕「うん、その通りだよ。ちゃんとテトラちゃんは理解している。大丈夫。ここまでで、こんな二本の式を得たことになる」

$$ \begin{cases} v_x &= \frac{d}{dt}x \\ v_y &= \frac{d}{dt}y \end{cases} $$

テトラ「はい。これからどんなお話に進むんでしょう」

僕「テトラちゃんは、どんな話に進むと思う？」

テトラ「あ、あたしがどう思うか……話の流れとして、あたしたちは速さ $v$ と角速度 $\omega$ の関係はわかってますね。 それから位置 $(x,y)$ と角度 $\theta$ の関係もわかっています。それからもちろん角速度 $\omega$ と角度 $\theta$ との関係もわかっています。 これらと、いまの速度ベクトル $\vec v$ の話をつなげる……んでしょうか？」

僕「そうだね。 等速円運動しているおもりについて、さまざまな物理量同士の関係を計算で導いたり確かめたりしているわけだから。 では具体的に速度ベクトル $\vec v$ と速さ $v$ の関係を考えるとして——テトラちゃんはわかる？」

テトラ「速さ $v$ は速度ベクトル $\vec v$ の大きさですから、 $$ v = \ABS{\vec v} $$ ですね」

僕「うん、それでいいよ。ところで $\vec v$ の成分は $v_x,v_y$ だとわかっているから、もう少し行ける」

テトラ「……あっ、はいはい。三平方の定理が使えますから、 $$ v^2 = v_x^2 + v_y^2 $$ ですね。そうでしたそうでした。速さは $0$ 以上なので、 $$ v = \SQRT{v_x^2 + v_y^2} $$ になりますっ！」

等速円運動をしているおもりで速度ベクトル $\vec v$ を考察する

僕「そうだね。いまのは速さと速度ベクトルの成分との関係。 ところで、おもりが等速円運動している場合、おもりの位置 $x,y$ は角度 $\theta$ で表せる。 これはさっきテトラちゃんが答えてくれた（第377回参照）」

テトラ「はい。 $x$ 座標は $\cos$ で、 $y$ 座標は $\sin$ で表せます」

$$ \vec x = \VECV{x}{y} = \VECV{r\cos\theta}{r\sin\theta} $$

僕「ここに出てきた角度 $\theta$ は時刻 $t$ の関数で表せるから、 結局、 $x,y$ は $t$ の関数として表せることになるね。

テトラ「角度 $\theta$ は時刻 $t$ の関数……あっ、それはそうです。 $$ \theta = \omega t $$ です」

僕「そうだね。角度の初期値、つまり $t = 0$ のときの角度を $\theta = 0$ としてるから、そうなる。 さてそれで、速度ベクトルがあちこちとつながるよね？」

テトラ「さてこれでつながるか……ああ、わかりました。 確かに位置ベクトルを時刻 $t$ で微分する》ことで、 ここまでこまごま出してきた式が一気につながりますね。 ちょっとやってみます！　まずは $v_x$ を $t$ で微分するところから……」

$$ \begin{align*} v_x &= \frac{d}{dt}x && \REMTEXT{} \\ &= \frac{d}{dt}(r\cos\theta) && \REMTEXT{$x = r\cos\theta$だから} \\ &= \frac{d}{dt}(r\cos\omega t) && \REMTEXT{$\theta = \omega t$だから} \\ &= -r\sin\omega t && \REMTEXT{$\cos$を微分して$-\sin$……あらら？} \\ &= \textbf{……とっとっと} \end{align*} $$

テトラ「……とっとっと。これ、合成関数の微分になるんですよね？　ということは $\omega$ を掛ける必要がありますか？」

$$ \frac{d}{dt}(r\cos\omega t) = -r\FOCUS{\omega}\sin \omega t $$

僕「そう！　その通り。引っかからなかったね！」

テトラ「えーと……それで、先ほどの続きを進めます」

$$ \begin{align*} v_x &= \cdots \\ &= -r\omega\sin\omega t && \REMTEXT{$\omega$を掛けるのを忘れない} \\ \end{align*} $$

僕「うん、同じように $v_y$ も計算できるね」

テトラ「大丈夫です」

$$ \begin{align*} v_y &= \frac{d}{dt}y && \REMTEXT{} \\ &= \frac{d}{dt}r\sin\theta && \REMTEXT{$y = r\sin\theta$だから} \\ &= \frac{d}{dt}r\sin\omega t && \REMTEXT{$\theta = \omega t$だから} \\ &= r\omega\cos\omega t && \REMTEXT{} \\ \end{align*} $$

僕「できたできた。これで速度ベクトル $\vec v$ が $t$ の関数で表せた」

$$ \vec v = \VECV{v_x}{v_y} = \VECV{-r\omega\sin\omega t}{r\omega\cos\omega t} = r\omega\VECV{-\sin\omega t}{\cos\omega t} $$

テトラ「ああ……これ、もしかして $v = r\omega$ が出てきませんか？　だって、 $$ (\sin \heartsuit)^2 + (\cos \heartsuit)^2 = 1 $$ ですから、速さ $v$ を三平方の定理で計算していくと、 $\sin$ と $\cos$ が消えますよね！！」

$$ \begin{align*} v &= \SQRT{v_x^2 + v_y^2} && \REMTEXT{速さ$v$は速度ベクトルの大きさだから（三平方の定理）} \\ &= \SQRT{(-r\omega\sin\omega t)^2 + (r\omega\cos\omega t)^2} && \REMTEXT{上で計算した$v_x,v_y$} \\ &= \SQRT{r^2\omega^2(\sin\omega t)^2 + r^2\omega^2(\cos\omega t)^2} \\ &= r\omega \SQRT{(\sin\omega t)^2 + (\cos\omega t)^2} \\ &= r\omega && \REMTEXT{$(\sin \heartsuit)^2 + (\cos \heartsuit)^2 = 1$だから} \\ \end{align*} $$

僕「おお！　気付くの早いなあ、テトラちゃん！」

テトラ「はい。 $\cos\heartsuit$ と $\sin\heartsuit$ が出てきたらすぐに、 半径の長さが $1$ の単位円を思い出しますから！」

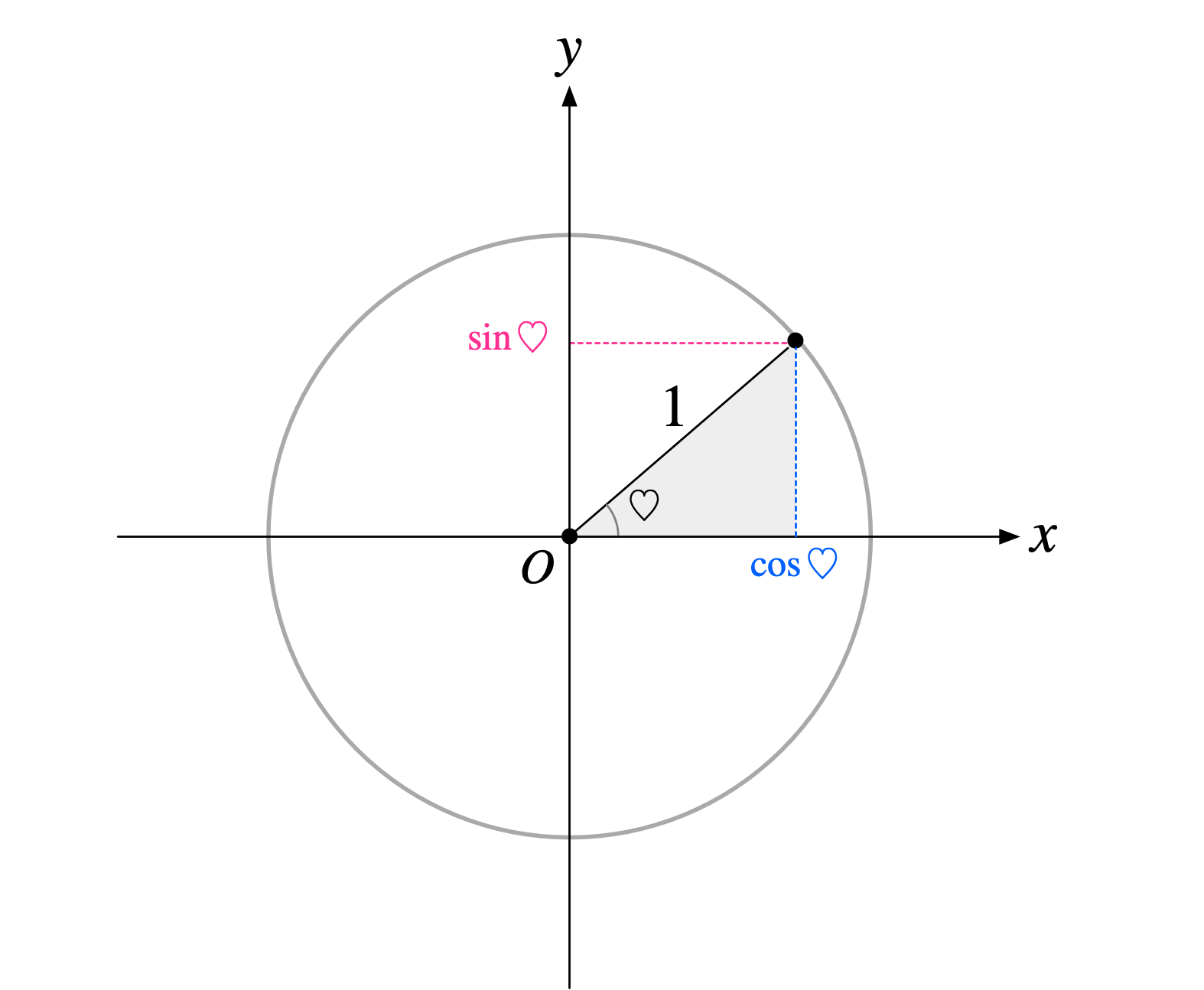
僕「そうだね」

テトラ「いまの計算は、 速さ $v$ と半径 $r$ と角速度 $\omega$ の関係を別ルートで検算したようなものですね。ちゃんと $$ v = r\omega $$ が出ました！」

僕「うん、でも、わかるのはそれだけじゃないよ。速さ $v$ は速度ベクトル $\vec v$ の《大きさ》だけど、 《向き》の情報を捨てているから。《向き》の情報を使って考えを進められる」

テトラ「《向き》の情報を捨てている？」

位置ベクトル $\vec x$ と速度ベクトル $\vec v$ の《向き》の関係

僕「速度ベクトルの成分がわかったから、位置ベクトル $\vec x$ と速度ベクトル $\vec v$ の《向き》の関係がわかるんだよ。 $\theta = \omega t$ を使って $\vec x$ と $\vec v$ を整理するとこうなる」

$$ \begin{align*} \vec x &= r\VECV{\cos\theta}{\sin\theta} \\ \vec v &= r\omega\VECV{-\sin\theta}{\cos\theta} \end{align*} $$

テトラ「速度ベクトルは、円の接線方向を向いてたはずですよね？」

僕「そうだね。そのことは直感的に納得した（第376回参照）。それをいまや式の上で確かめられるんだよ！」

テトラ「す、すみません。まだあたしはピンと来ていないようです」

僕「速度ベクトルが円の接線方向を向いてるってことは、 速度ベクトルは位置ベクトルと直交していることになる。 零ベクトルを除いて考えると、 《二つのベクトルが直交しているかどうか》は《二つのベクトルの内積が $0$ かどうか》でわかる。 だから、 $\vec x$ と $\vec v$ の内積 $\vec x \cdot \vec v$ を計算しよう！」

$$ \begin{align*} \vec x \cdot \vec v &= \VECV{x}{y} \cdot \VECV{v_x}{v_y} \\ &= xv_x + yv_y \qquad \REMTEXT{ベクトルの内積を成分で計算} \\ &= (r\cos\theta)(-r\omega\sin\theta) + (r\sin\theta)(r\omega\cos\theta) \\ &= -r^2\omega\cos\theta\sin\theta + r^2\omega\sin\theta\cos\theta \\ &= 0 \end{align*} $$

テトラ「あっ！　きれいに消えましたね……なるほど。 微分すると $\cos$ からは符号が変わった $-\sin$ が出てきて、 $\sin$ からは $\cos$ が出てきます。 入れ替わって符号が変わるので、内積を取ると $0$ になる！　おもしろいですねえ……」

僕「おもしろいよね。つまり、位置ベクトルを時刻 $t$ で微分して速度ベクトルを得ると、 速度ベクトルの《大きさ》に関しては、 $$ v = r\omega $$ ということが、三平方の定理の助けを借りて確かめられる。これは速さ $v$ と半径 $r$ と角速度 $\omega$ の関係」

テトラ「はいはい」

僕「そして、速度ベクトルの《向き》に関しては、 $$ \vec x \cdot \vec v = 0 $$ から内積の助けを借りて、位置ベクトルと速度ベクトルが直交していることがわかる。 僕たちは速度ベクトルの《大きさ》と《向き》を押さえたことになる」

テトラ「ああ……なんだかすごくつながった感じがします！」

僕「そしてもちろん、もう一歩進みたくなるよね！」

テトラ「もちろんです。速度ベクトルを時刻 $t$ で微分して、加速度ベクトルを得るわけですねっ！」

加速度ベクトル $\vec a$