![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
僕「……そんなふうに、極座標で遊んでいたんだよ」
テトラ「なるほど、おもしろいですねえ……」
ここは僕の高校の図書室。いまは放課後。
いつものように僕はテトラちゃんとおしゃべりをしていた。
極座標のこと(第361回参照)、アルキメデス・スパイラルのこと(第362回参照)、花のような曲線のこと(第363回参照)、 そして、描かれた図形の正体を数学を使って確かめること(第364回参照)。
僕はそんな話を詳しくテトラちゃんに伝えた。
僕「テトラちゃんは正方形を描いたことがあったよね。あれもおもしろかった(第90回参照)」
テトラ「あたしというよりも、ミルカさんに教えていただいたようなものですが……でも、楽しかったですっ!」
僕「描いた図形はパッと見ても楽しいけど、数式で表せるなら、いろんな性質が確かめられて楽しいよね」
テトラ「そうですね……あたしが印象深く感じるのは、先輩のお話にもありましたが、 『図形は点の集まり』というところです(第361回参照)」
僕「そうだね。平面上に描かれた図形を、平面上の点の集まりだと考えてる」
テトラ「それって、とても大事なことですよね。だって……点の話をすればいいからです」
僕「点の話?」
テトラ「はい。点の話、です。 一つの点について考えるんですけれど、そこには文字が含まれていて、 その文字に具体的な数値が入ります。だから、その数値を変えることで《点の話》がいつのまにか《図形全体の話》に なっている。そんなふうに思っています」
テトラちゃんは両手をくねくねと動かしながらそう話した。
たぶん、両手で《図形全体》を表しているんだろうな。
僕「まさに! まさにそうだよね。文字を使って表しておけば、《点の話》がすうっと《図形全体の話》になる。 うん、テトラちゃんの言うとおりだ。 ユーリと話していたときには《数式は無限と戦う武器になる》と言ってたなあ。 『武器になる』というときには、僕はテトラちゃんのことを思い出してたよ。テトラちゃん、よく武器を構えるよね」
テトラ「お、思い出していただけるのは光栄ですが……《よく武器を構える》としてあたしを思い出されるのはちょっと」
テトラちゃんは、わざとらしく頬を膨らませる。
僕「ごめんごめん」
テトラちゃんは吹き出し、僕たちは大笑いした。
テトラ「先輩は直交座標よりも極座標の方が『回転が得意』とおっしゃっていました(第361回参照)が、 あたしはお話を聞きながら別のことを考えていました」
僕「へえ……どんなことだろう」
テトラ「あのですね、極座標の方が『一つの点が動いていく』感じがするんです。 極座標では、動径が $r$ で、偏角が $\theta$ のとき、 $$ r = \TEXT{《$\theta$の式》} $$ という形がよく出てきますよね。 $\theta$ を決めると $r$ が決まりますから、 ちょうどコンパスを回すように一つの点がすうっと動いていく感覚があります……あ、 でも、これって結局は『回転が得意』と同じことですけど」
僕「いや、でも、テトラちゃんの感覚はわかるよ。僕もそう思う。 $$ r = \TEXT{《$\theta$の式》} $$ で、 $\theta$ というパラメータに図形が支配されている感じというのかな。 支配というと大げさだから、制御というかコントロールというか……」
$r = \TEXT{《$\theta$の式》}$で図形が$\theta$に制御されているイメージ図

テトラ「パラメータ……」
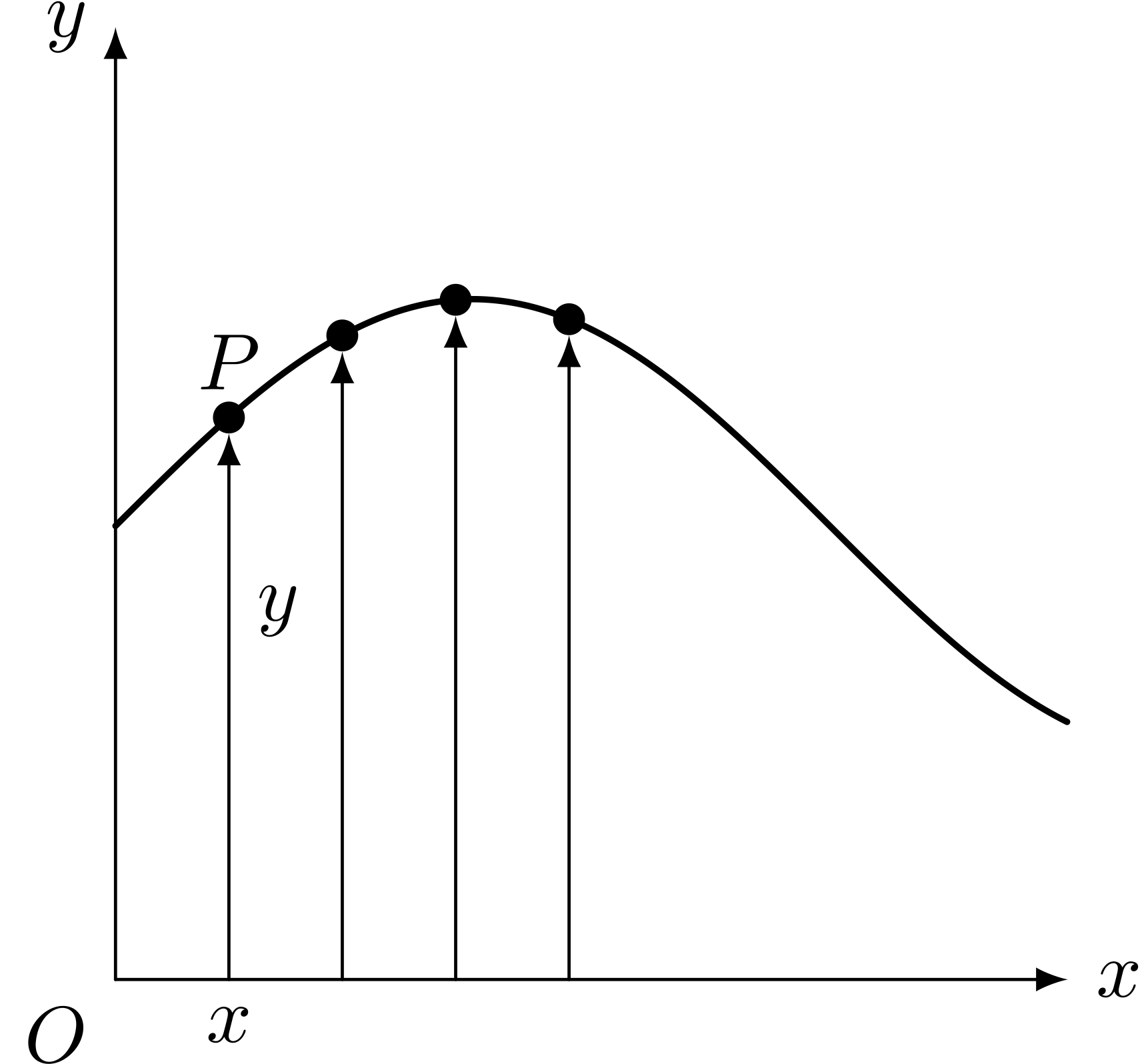
僕「うん。もっとも、直交座標でも、たとえば、関数のグラフみたいに、 $$ y = \TEXT{《$x$の式》} $$ という形なら、『一つの点が動いていく』感じはするよね。 $x$ の値を決めれば $y$ が決まるから、 $x$ の値で図形が制御されている感覚がある」
$y = \TEXT{《$x$の式》}$で図形が$x$に制御されているイメージ図
テトラ「そ、そのパラメータの話をもう少しお聞きしたいです。 あたしが持ってる感覚がはっきりするような気がします」
僕「うん、いいよ。ものすごく単純な例。 半径が $a$ の円を直交座標で表すことにするね」
テトラ「はい」
僕「直交座標で、原点が中心にある、半径が $a$ の円を表す方程式は、 $$ x^2 + y^2 = a^2 $$ と書ける。これはいいよね」
テトラ「はい、大丈夫です」
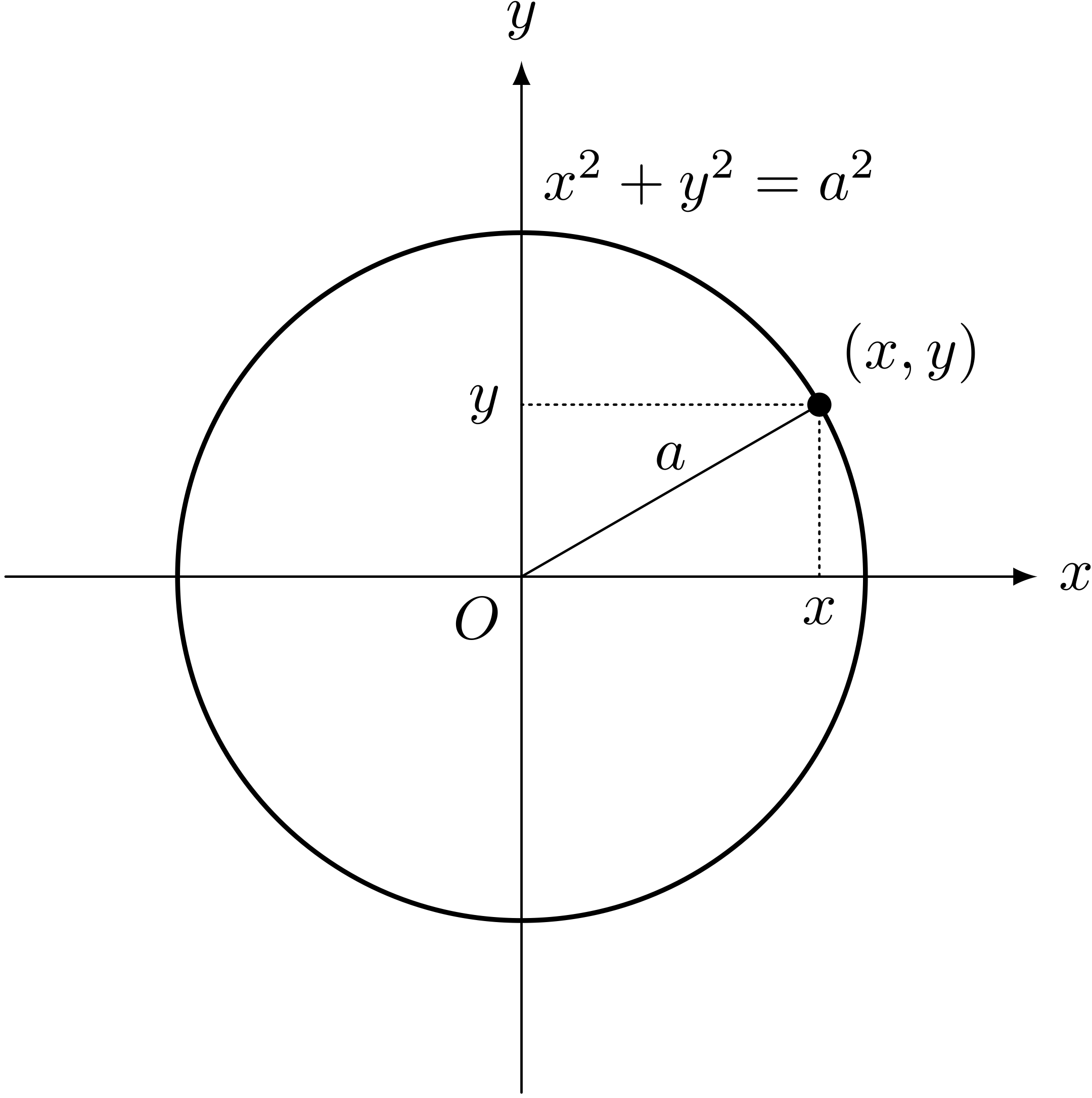
僕「この $x^2 + y^2 = a^2$ という書き方だと、《円上の点 $(x,y)$ は、 $x$ の座標値と $y$ の座標値がどういう関係を満たしているか》を表している」
テトラ「そうですね。 原点 $(0,0)$ からの距離が $a$ になっている……ということですよね?」
中心が原点 $(0,0)$ にあり、半径が $a$ の円を $x^2 + y^2 = a^2$ と表す
僕「うん、そうそう。だから『一つの点が動いていく』感じはあまりしない」
テトラ「……」
僕「でも同じ直交座標で同じ円を、 $\theta$ というパラメータを使ってこう表現してみよう」
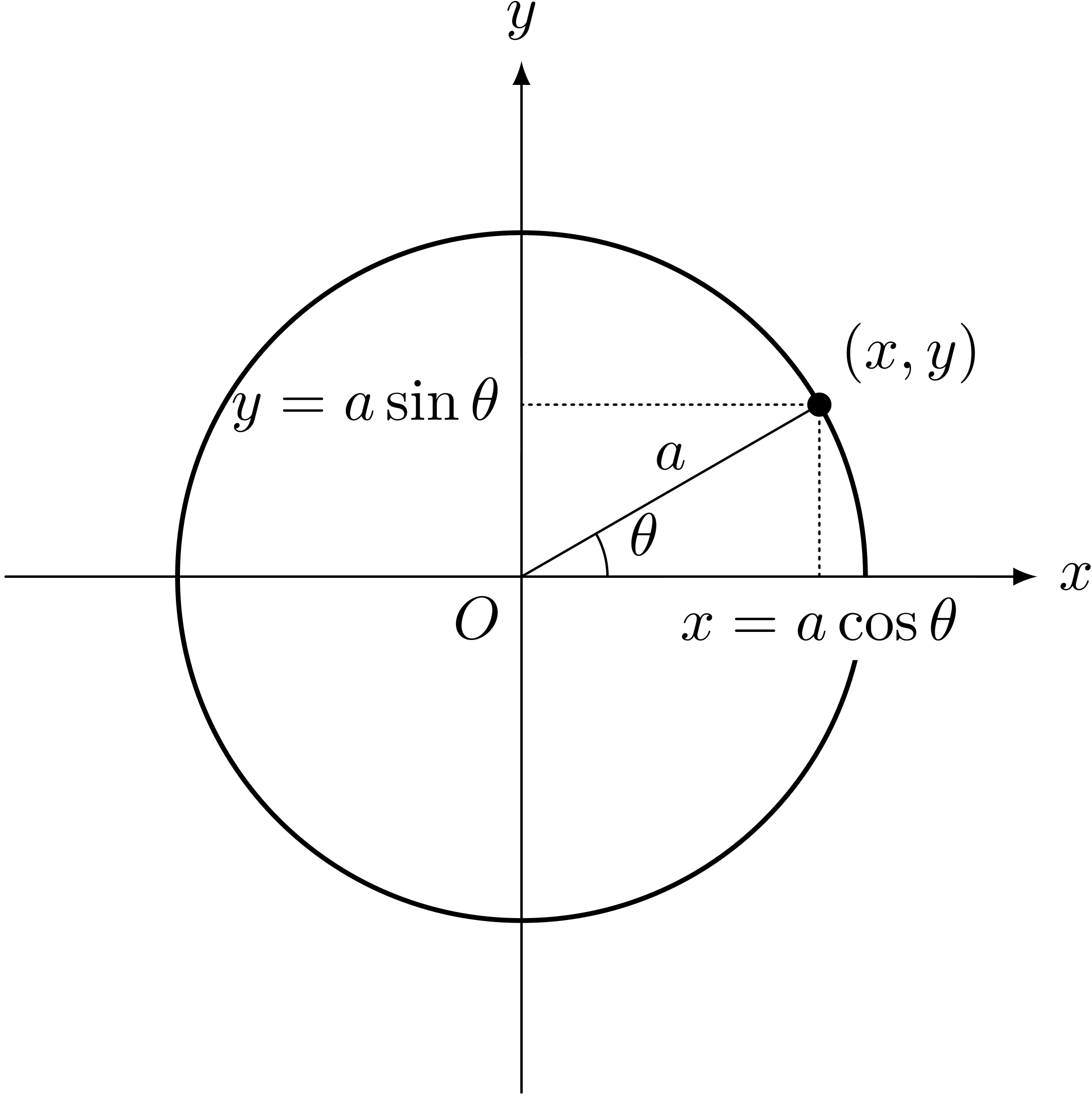
$$ \left\{\begin{array}{llll} x &= a\cos\theta \\ y &= a\sin\theta \\ \end{array}\right. $$テトラ「ははあ……わかりました! これだと、 $\theta$ というパラメータの値を変えていくことで、 $x$ と $y$ の値がすうっと変わっていきます。だから『一つの点が動いていく』感じがしますね!」
中心が原点 $(0,0)$ にあり、半径が $a$ の円を $\theta$ を使って表す
$$ \left\{\begin{array}{llll} x &= a\cos\theta \\ y &= a\sin\theta \\ \end{array}\right. $$
僕「そういう話。ただ、これはあくまでも感覚的な話。 というのは、 $x^2 + y^2 = a^2$ という式を少し変形すれば、同じようなことができるから。 たとえば、こんな式で表せば、 $x$ の値を変えていくことで $y$ の値が変わっていくようすがわかる」
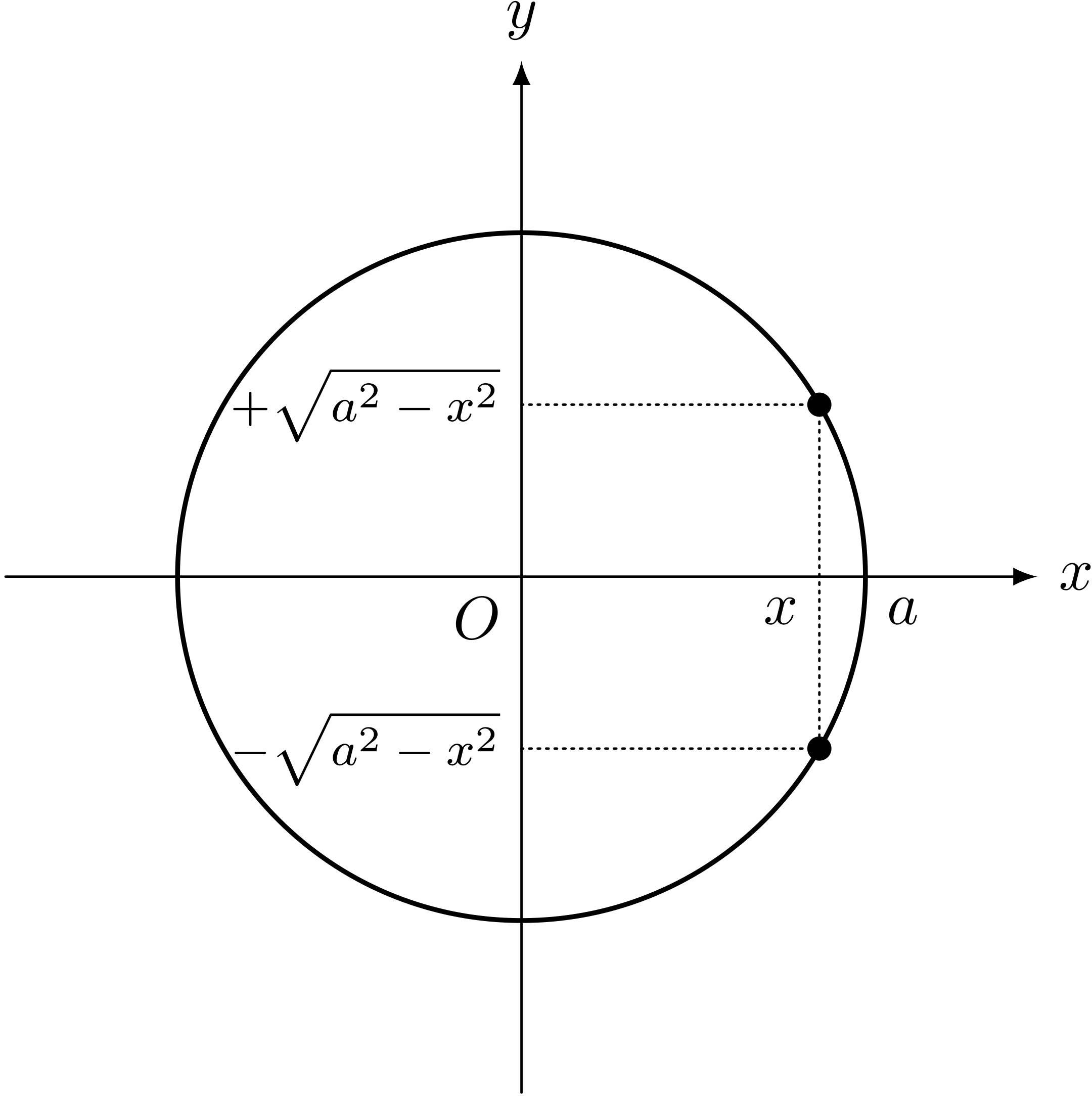
$$ y = \pm \SQRT{a^2 - x^2} $$テトラ「確かに……あっ、でも、これだと動いていくのは『二つの点』ですよね。 だって、 $x$ の値一つに対して、 $y$ の値は $y = +\SQRT{a^2 - x^2}$ と $y = -\SQRT{a^2 - x^2}$ という二つの値になりますから」
僕「おっと、そうだね。確かにそうだ」
中心が原点 $(0,0)$ にあり、半径が $a$ の円を $y = \pm \SQRT{a^2 - x^2}$ で表す
テトラ「花のような図形の極方程式を調べるとき、先輩は横軸が $\theta$ で縦軸が $r$ の直交座標をお使いになりましたよね」
僕「そうだね。もともとユーリが描いていたんだけど。 $r = \sin^25\theta$ のグラフだね」
花の図形の極方程式 $r = \sin^25\theta$

$r = \sin^25\theta$ のグラフ($\theta$ と $r$ を直交座標で表した。 $\theta$ はラジアン)
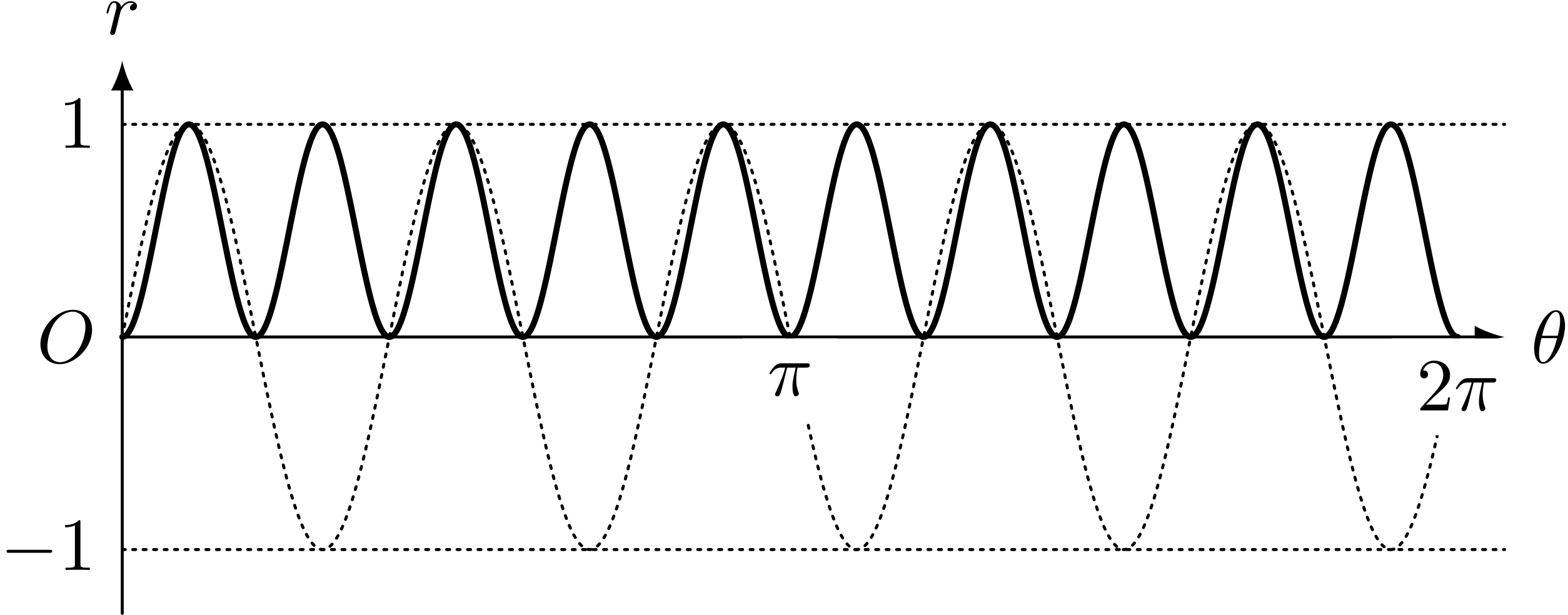
テトラ「あれはまさに、 $\theta$ を動かしていくときの $r$ の変化を表していると思いました」
僕「うん」
テトラ「ところで、すごくおもしろいことに気付いたんですよ。 単位円の極方程式は、 $$ r = 1 $$ ですよね?」
僕「そうだね。単位円は偏角 $\theta$ によらず動径の長さが $1$ になるから。……おもしろいことって?」
テトラ「はい。 横軸が $\theta$ で縦軸が $r$ の直交座標で、単位円を表すと、こんなふうに横一直線になります。 $r$ が変化しないんだから当然ですけれど」
単位円の極方程式 $r = 1$
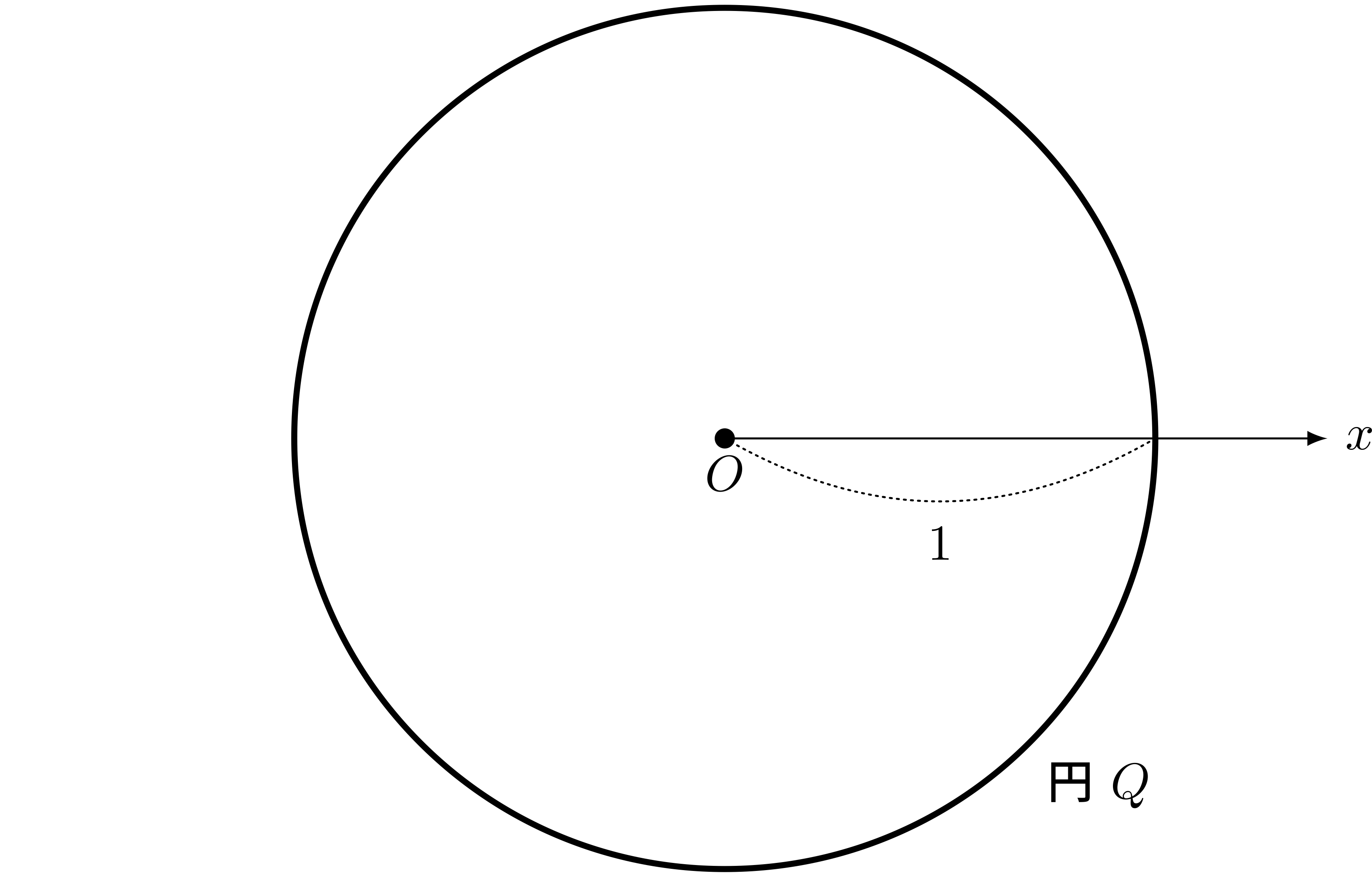
$r = 1$ のグラフ($\theta$ と $r$ を直交座標で表した。 $\theta$ はラジアン)
僕「うん、そりゃそうだ」
テトラ「つまり、円が円であることが、《まっすぐなグラフ》として表現されている! ……とあたしは思ったんですっ!」
僕「そうだね」
テトラ「あ、あらら……先輩の反応、薄いですね」
僕「うーん……テトラちゃんの感動ポイントがよくわからなかったんだ。ごめんね」
テトラ「ええっ! 円がちょうどよく《丸い》ことが《まっすぐ》なグラフに現れているんですよっ! ……あたし、おもしろいと思うんですが……」
僕「うーん……あ、待って。アルキメデス・スパイラルについても同じことが考えられるね(第362回参照)」
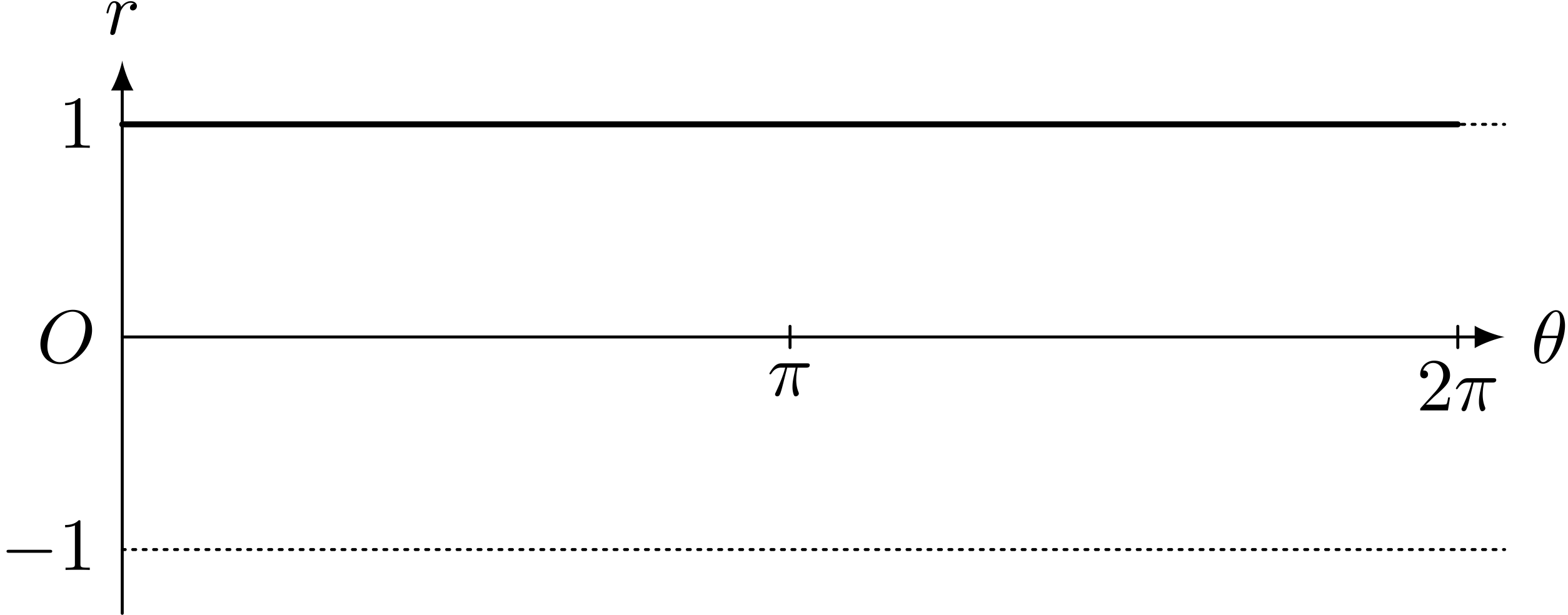
アルキメデス・スパイラルの極方程式 $r = \theta$ $(0 \LEQ \theta < 2\pi)$
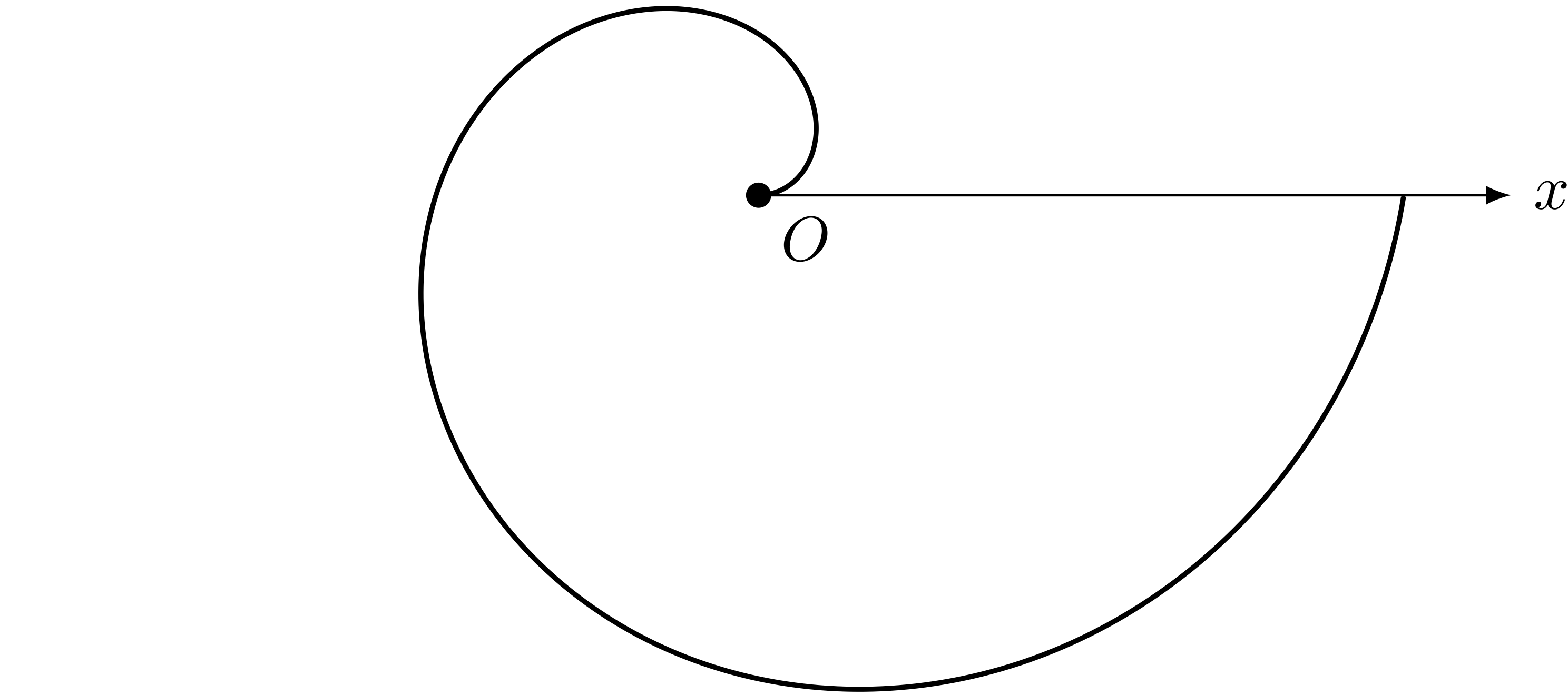
$r = \theta$ のグラフ($\theta$ と $r$ を直交座標で表した。 $\theta$ はラジアン)
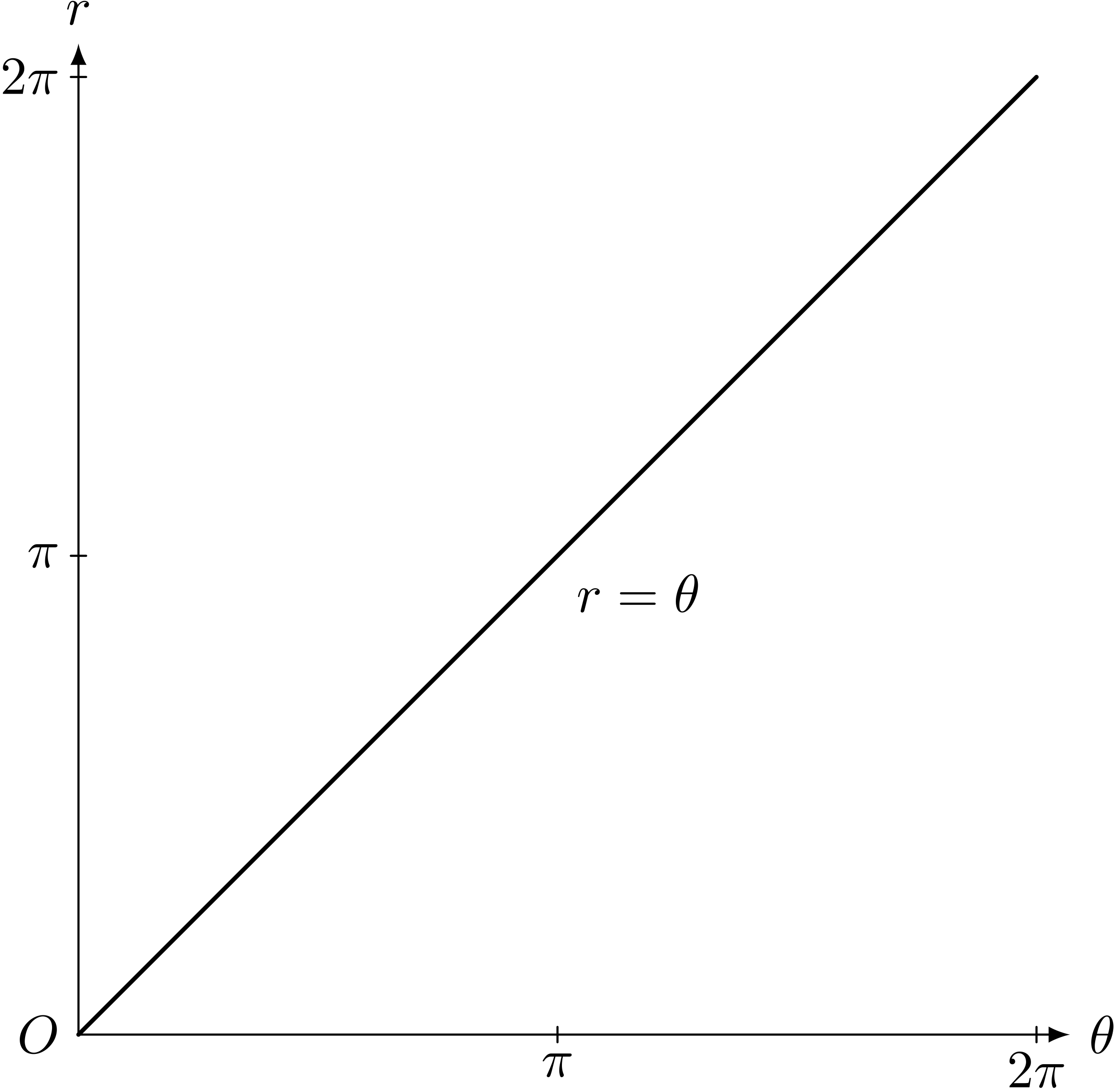
テトラ「ははあ……こちらも《まっすぐなグラフ》になります」
僕「うん、だから、そういう意味では、円とアルキメデス・スパイラルは仲間だといえる」
テトラ「仲間? ええと……そうなんでしょうか」
僕「仲間というか……何というのかな。 円とアルキメデス・スパイラルを一つの式の別の形として考えることもできそうだと思ったんだけど」
テトラ「?」
僕「ちょっと待って。いま考えながらしゃべっているから、ウソ言ってるかもしれない……つまりね、 アルキメデス・スパイラルの極方程式は、一般的に書けば $c$ を定数として、 $$ r = c\theta $$ になる」
テトラ「$c$ が大きければ、すばやく広がるらせんになる?」
アルキメデス・スパイラル三種類($r = c\theta$ で $c = 1,2,3$ にした)

僕「そうそう。そこで $r = c\theta$ の $c$ を $0$ にするとうまいこと円に……いや、円にはならないな、だめか。 ……いや、わかった。別の定数を用意すればいいんだよ」
テトラ「先輩は……何をなさっているんでしょう」
僕「うん、もたもたしてごめん。もうわかった。 $c$ と $d$ を $0$ 以上の定数として、 $$ r = c\theta + d $$ という極方程式を考えるんだよ!」
テトラ「はい……偏角 $\theta$ を $c$ 倍して $d$ を加えたものが動径 $r$ に等しいとする……?」
僕「うん。そうすると……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年8月19日)