![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ここは僕の高校の図書室。いまは放課後。
僕とテトラちゃんの数学トークはまだ続いている。
僕とユーリがおしゃべりしていた話題として、 極座標(第361回参照)、アルキメデス・スパイラル(第362回参照)、花のような曲線(第363回参照)、 数学を使って確かめる図形の正体(第364回参照)の話をした後、 テトラちゃんは、直線上を転がる円が描く曲線のクイズに挑戦していた(第365回参照)。
テトラ「はい、これで解けました! 《滑らずに転がる》という重要なヒントをありがとうございます!」
第365回最後のクイズの答え
半径 $1$ の円板を転がしたときに生まれる図形を調べます。
最初に、円板の中心が点 $(0,1)$ に来るように置きます。

このとき、原点 $(0,0)$ にある円板上の点を $P$ として、この点 $P$ の動きに注目します。
円板を $x$ 軸の上を滑らずに転がしていくと、 円板が転がるにつれて、点 $P$ は一つの曲線を描いていきます(曲線は青、赤い線は転がった長さ)。

この曲線上の点を $(x,y)$ としたとき、 転がる角度を $\theta$ ラジアンとして、
$$ \left\{\begin{array}{llll} x &= \theta-\sin\theta \\ y &= 1-\cos\theta \end{array}\right. $$ という式が成り立ちます。
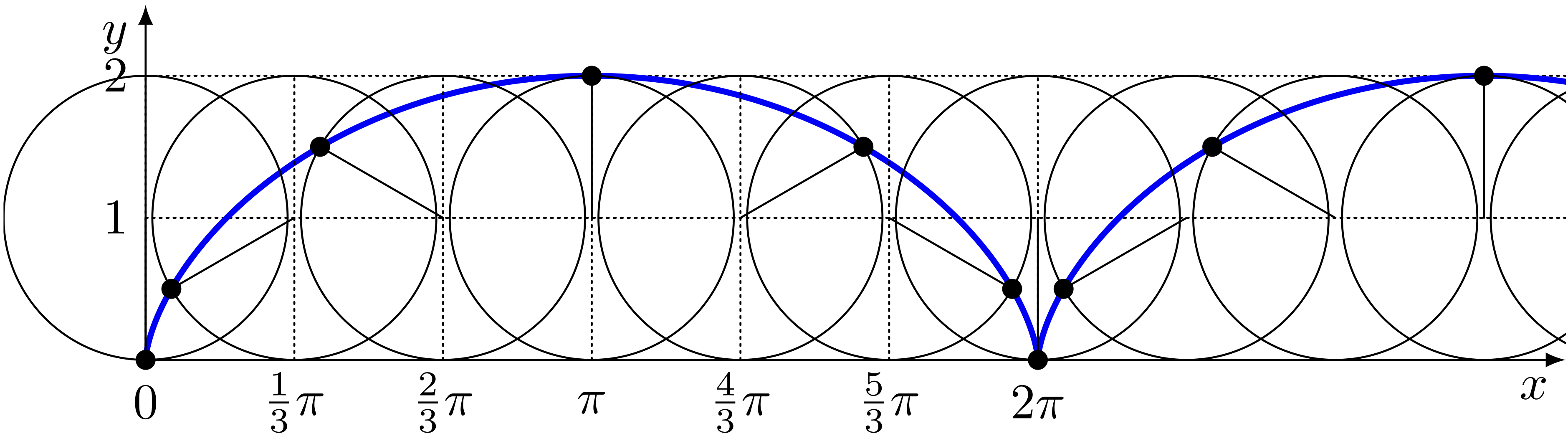
点 $P$ が描く曲線の概形を、 $\theta$ を $\tfrac23\pi$ ずつ増やした円板のようすと共に描くと次のようになります。

また、 $\theta$ をさらに細かく $\tfrac13\pi$ ずつ増やした円板のようすと共に描くと次のようになります。
僕「こういうクイズ、おもしろい?」
テトラ「はい!……これは楕円とも違いますよね?」
僕「そうだね。この図形は一般にサイクロイドと呼ばれている曲線の一つになるね」
テトラ「サイクロイド……サイクルに関係した言葉のようです」
僕「うん。そうだね……綴りはcycloidだよ。 円が回転するところから生じる図形だからこういう名前が付いているんだと思うな。 いまは半径が $1$ の円をもとにしたサイクロイドだったから、 $$ \left\{\begin{array}{llll} x &= \theta-\sin\theta \\ y &= 1-\cos\theta \end{array}\right. $$ という式で表せたけど、一般に半径が $R$ の円をもとにしたサイクロイドは、 全体を $R$ 倍して、 $$ \left\{\begin{array}{llll} x &= R(\theta-\sin\theta) \\ y &= R(1-\cos\theta) \end{array}\right. $$ と表せることになるね」
テトラ「なるほどです。おもしろいですねえ……」
僕「そんなに喜んでもらえるなら、これにそっくりな別のクイズに挑戦してみる?」
テトラ「ぜひぜひ!」
僕「もしかしたら、テトラちゃんはすでに見たことがあるかもしれないけどね。 さっきのクイズでは、円板を直線に沿って転がしたよね」
テトラ「そうですね。 $x$ 軸に沿って転がしました」
僕「今度は、円板を別の円板に沿って転がすんだ」
テトラ「先輩は、いろんなことをご存じですね」
僕「いや、今回のクイズは僕もちゃんと考えたことはないんだよ。 でも、テトラちゃんが楽しそうにしているから、似た問題を僕も考えたくなったんだ」
テトラ「へえ……」
僕「こういうクイズにしよう」
クイズ(円板に沿った回転)
半径 $1$ の円板を転がしたときに生まれる図形を調べます。
最初に、半径 $1$ の円板 $O$ を中心が $(0,0)$ に来るように置いて固定します。
次に、半径 $1$ の別の円板 $Q$ を、中心が $(0,2)$ に来るように置いて、この円板 $Q$ を円板 $O$ に沿って転がしていきます。 このときに滑らずに転がさなくてはいけません。 さらに、最初に点 $(0,1)$ にある円板 $Q$ 上の点を $P$ として、この点 $P$ の動きに注目します。

円板 $Q$ を、円板 $O$ に沿って転がしていくとき、 円板 $Q$ が転がるにつれて、点 $P$ は一つの曲線を描いていきます。その曲線の描き始めの様子を、 下図では青い線で示します。
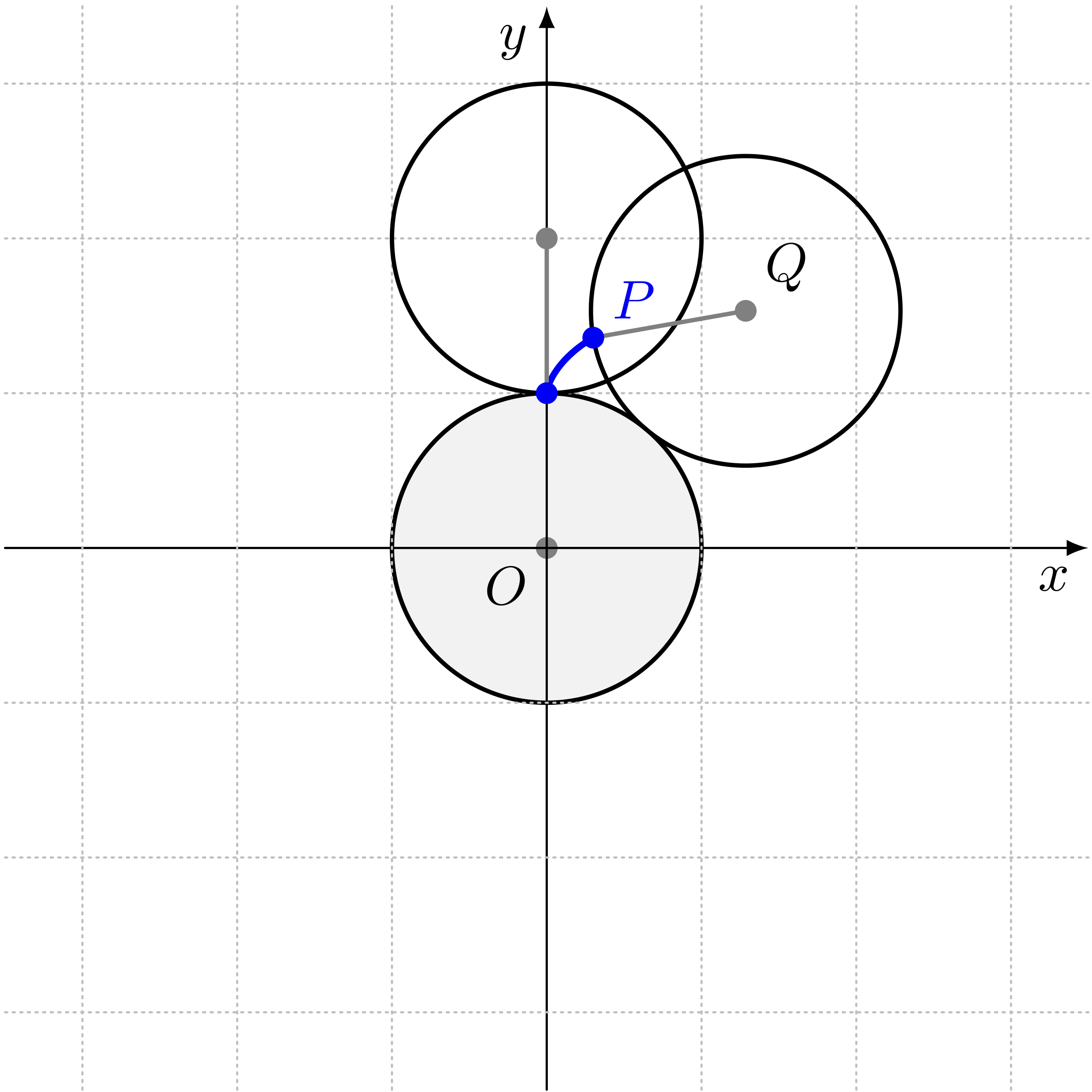
点 $P$ が描くこの曲線上の点を $(x,y)$ としたとき、 $x$ と $y$ が満たす式を求めてください。
テトラ「あっ、はいっ! あたし、これも見たことがありますっ! で、 でも、やはりちゃんと考えたことはありませんでした。 確かこれ、数学の本で見たのではなくて何かのクイズの本で見たんだと思います」
僕「クイズの本?」
テトラ「はい。 一つのコインを、別のコインの回りでぐるっと回したときに、何回転するでしょうかというクイズです。 この図でいいますと、円板 $Q$ は円板 $O$ の回りをぐるっと回りますよね。そしてやがてまた、もとの位置に戻ってくることになります」
僕「そうそう。そうなるよね」
テトラ「ではひとまわりして、円板 $Q$ がもとの位置まで戻ってきたら、そのときまでに円板 $Q$ は何回転していることになるでしょうかっ! そういうクイズです。 予想とは違う、意外な回数だけ回るんですよ」
僕「意外な回数……そうなんだ。ええと、ちょっと図を描いてもいい?」
テトラ「先輩、先輩。図に描かずに、頭の中だけで考えてみてください! 円板 $Q$ を円板 $O$ のまわりに転がしていったときに、 ぐるっと回ったら、円板 $Q$ は何回転するでしょうか?」
クイズを出したのは僕だけど、テトラちゃんの逆襲にあってしまった。
僕「え、そんなに意外な回数になるのかなあ? だって、一回転だよね。 円板 $Q$ と円板 $O$ は半径が等しいんだから、円周の長さも等しいはずだよ。 円板 $Q$ と $O$ の円周の長さは等しいことになる。だとしたら、 一回転して元のところに戻るんじゃないの? ズレないし、滑らずに転がるんだから。ちょうど歯車みたいに……」
テトラ「円板 $Q$ は一回転、でファイナルアンサーですか?」
僕「うーん、めちゃめちゃ図を描きたい!」
テトラ「そこを何とか想像してくださいっ!」
僕「いや、ちょっと待って。一回転して戻るんだったら、当たり前すぎるよね。だから、わざわざテトラちゃんはクイズにしたりしないはず。 でも、頭の中でコインを回しても、よくわからないんだよ。 図をちょっと描けばわかりそうなんだけど……」
僕はちらっとテトラちゃんを見るけれど、彼女はうれしそうに両手でバッテンを作る。駄目です、ということだ。
うーん……
テトラちゃんのクイズ
円板 $Q$ が円板 $O$ の回りを滑らずに転がって、はじめの位置まで戻ったとき、 円板 $Q$ は何回転していることになるでしょうか。
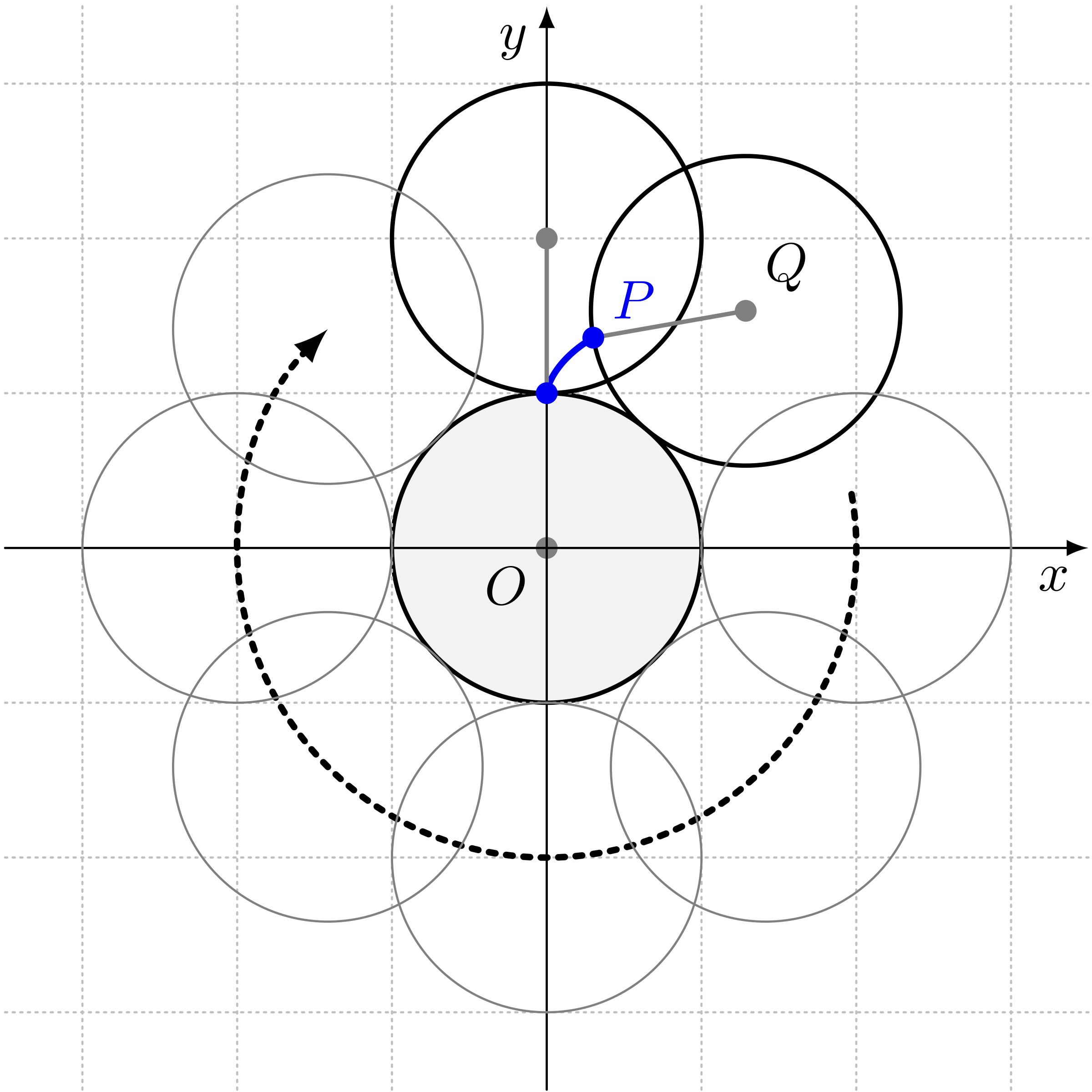

テトラ「……」
僕「……」
テトラ「……先輩、いかがですかっ?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年8月26日)