![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは極座標について図形を描いている。
極座標で $r = 1$ が単位円を表すという話題を話したり(第361回参照)、アルキメデス・スパイラルを描いたり(第362回参照)、まるで花のような曲線を描いたり(第363回参照)。
ところが描いているうちに……
僕「……ところでさっき花びら $2$ 枚になったよね。 $r = \ABS{\sin\theta}$ を描いたとき(第363回参照)」
極方程式 $r = \ABS{\sin\theta}$ が描く図形(再掲)

ユーリ「なったね。まんまる花びらが $2$ 枚できた」
僕「これって、円だと思う?」
ユーリ「えっ、円じゃないの? 二つの円だと思ってた」
僕「そうだね。二つの円に見えるけど……本当に円なのかなって思ったんだよ」
ユーリ「円か、円じゃないかなんて、わかんないよ〜」
僕「いや、調べることはできそうだよ」
クイズ
極方程式 $r = \ABS{\sin\theta}$ が描くこの図形は、円が二つのようだ。
でも、本当だろうか。
どうやったら、確かめることができるだろう。

ユーリ「いやいや、クイズ形式にしたからって、わかんないって!」
僕「そんなことないよ。クイズにしてみると、何を考えればいいかはっきりするから。 円が二つのように見えるけど、本当に $r = \ABS{\sin\theta}$ が描いてるのは円なんだろうか。 どうやったら、確かめることができるだろう」
ユーリ「円かどうか、形を調べるんじゃないの? 学校でもよくやるよ。 『じゃあ、みんなで調べてみましょう』って先生が言うの。 みんなで!とか言っても、実際に調べるのは一人一人だけど……」
僕「円かどうか、形を調べたい。それはそう。 $r = \ABS{\sin\theta}$ という極方程式が描く形を調べるんだけど……うん、 だから問題は、何が言えたら『これは円だ』とわかるのかってことだ」
ユーリ「ふむふむ。お兄ちゃんがよく言うヤツだ。《定義にかえれ》でしょ?」
僕「そうだね。いくら《円》という言葉をいじっても、何も出てこない。 円の《定義》に立ち返って考える必要がある。そのためのポリアの問いかけが《定義にかえれ》になる。 円の定義というのは、すなわち『円とは、こういうものである』というはっきりした説明のことだね。 円の定義は『こういうものを、円という』って表現のときもある」
ユーリ「ユーリ、それはわかってんの!」
僕「いや、さっき『わかんないよ〜』って泣いてたから、 考えを進める手がかりとして……」
ユーリ「ちがうの! 円の定義を気にしてるんじゃなくて、 どうやったら、その定義をこの『花びら二枚』に当てはめられるかがわかんないの!」
僕「なるほど。そっちなんだね。ところで、念のため……円の定義は?」
ユーリ「『一点から等距離にある点の集合』が円でしょ?」
僕「……」
ユーリ「うん? あーっと、違う違う! 平面上で一点から等距離にある点の集合!」
僕「そうだね」
ユーリ「平面上っていわないと球面かもしれないから」
僕「ユーリはすごくよくわかってる」
ユーリ「へへ」
僕「もうちょっとだけ言葉を補うと、 平面上で、ある一点から等距離にある点全体の集合を円という、 の方がよりいいね」
ユーリ「全体?」
僕「うん。ある一点から等距離にある点を集合の要素として集めるんだけど、 一部じゃなくて全部を集める。《全体》という言葉を使うと、全部を集めるんだってことがはっきりするから」
ユーリ「へー」
僕「それから、円の定義に出てくる《一点》のことを、その円の中心という」
円
平面上で、ある点 $A$ から等距離 $\ell$ にある点全体の集合を円という。
このときの点 $A$ をこの円の中心という。
中心 $A$ と、この円上にある点との距離 $\ell$ を、この円の半径という。
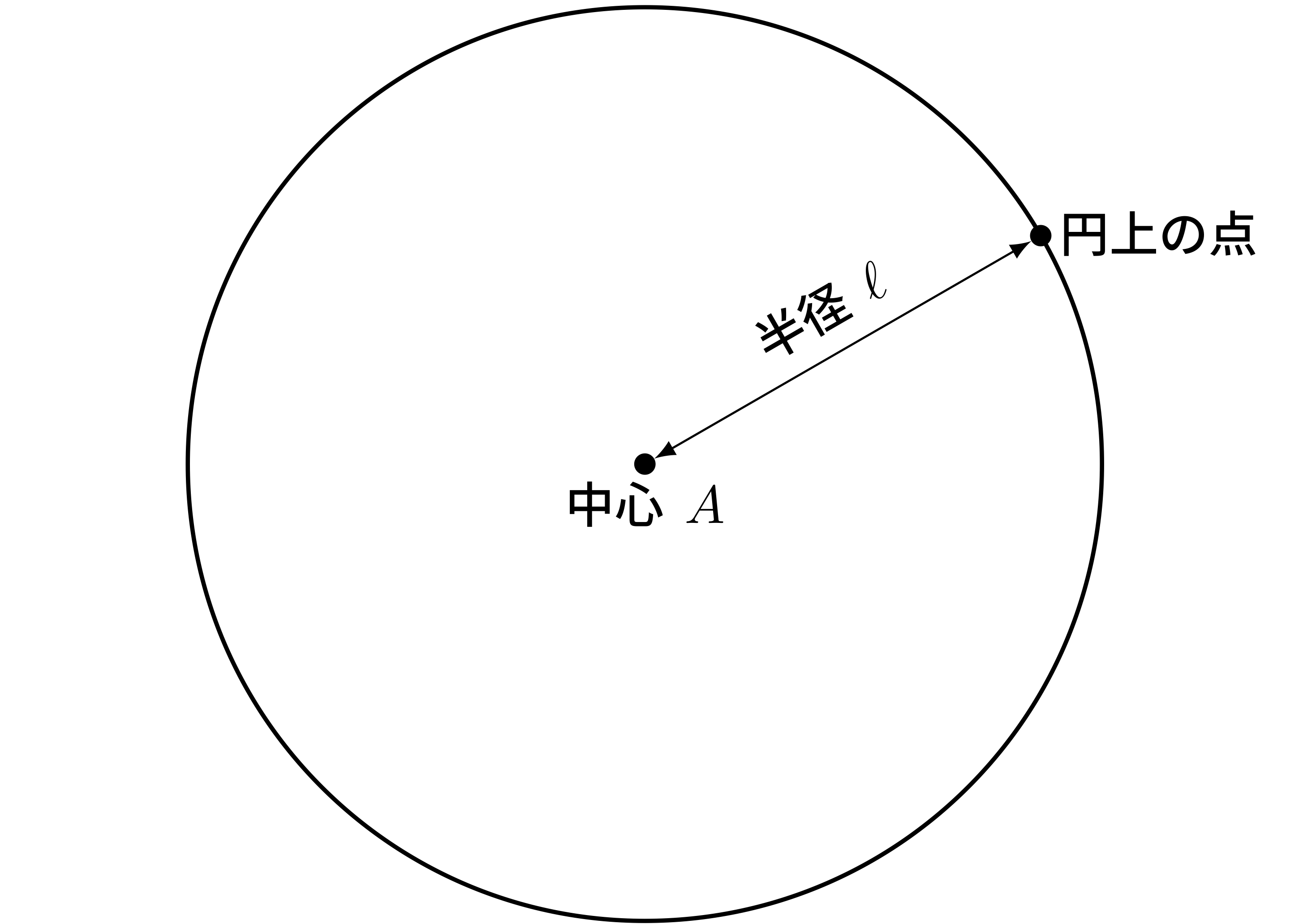
ユーリ「円の定義はわかってるし、中心の定義も、半径の定義もわかってるって」
僕「はいはい」
ユーリ「でもね、この『花びら二枚』でどーやったら、平面上で一点から等距離にあるってわかんの?」
僕「うん、そうだね。 ユーリは円、中心、半径の定義を知っている。 そしていま、すごくいいことを言った」
ユーリ「ほえ?」
僕「『どーやったら、平面上で一点から等距離にあるってわかんの?』って言った。 考えが前進しているよね。
ユーリ「うっわー……すっげーくどい」
僕「がく!」
ユーリ「何だか、当たり前のことを、ぎゅーっと引き延ばしてしゃべってるみたい」
僕「そんなことないよ。だって実際、考えを進める手がかりがちゃんと現れてきているだろ?」
ユーリ「んん?」
僕「試しに調べることが、はっきりした。 《円の中心になりそうな点》と《この図形上の点》との距離を調べることだよね!」
ユーリ「そりゃそーか……円の中心は、こことここでしょ? もしもこれが円だとしたら」
円だとしたら、中心はこことここ

僕「まずは、上の方で考えてみようか。 《円の中心になりそうな点》をたとえば $A$ として、 《図形上の点》をたとえば $P$ として、 二点 $A$ と $P$ の距離を調べることになる。 図形上のどこに点 $P$ を選んでも、距離が等しければ円になる!」
ユーリ「おっおっ、確かに!」
僕「《定義にかえれ》から、考えるべきことがはっきりしたことになるよね」
《円の中心になりそうな点 $A$》と《図形上の点 $P$》との距離を調べよう
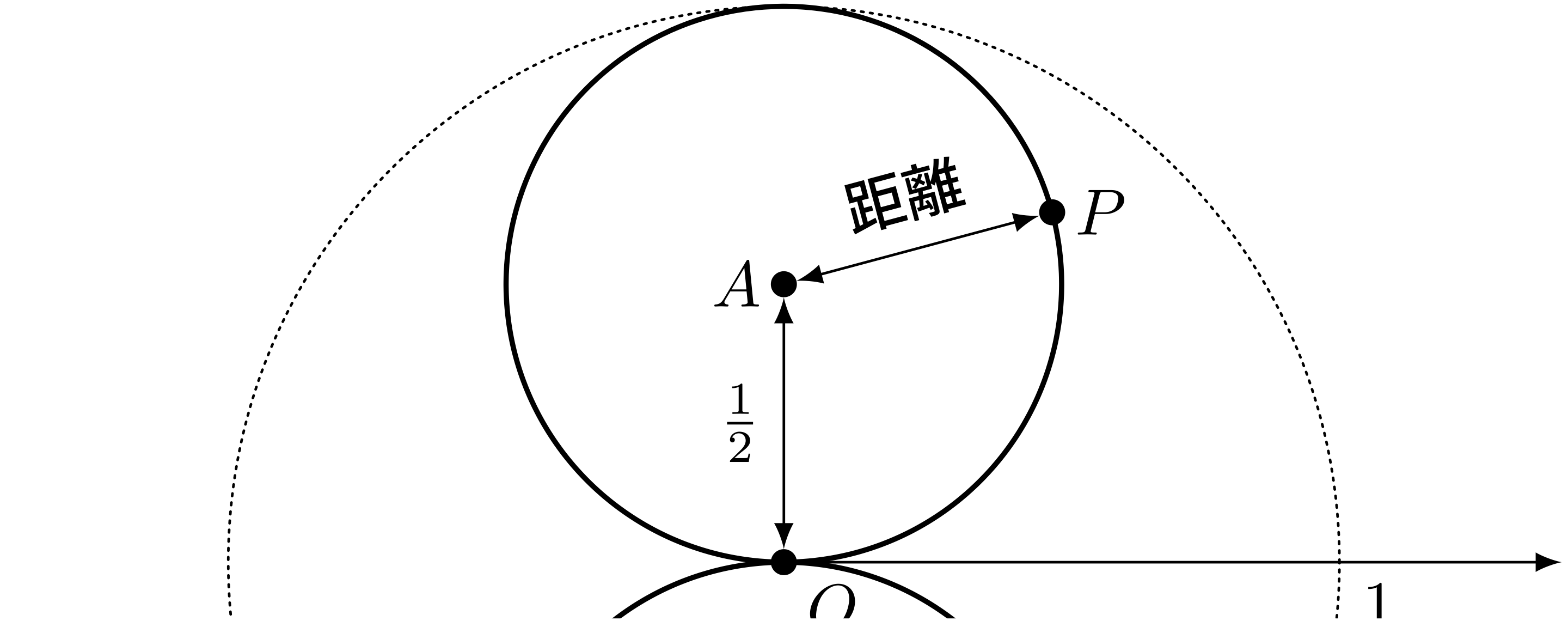
ユーリ「距離……距離なんて、わかるの? $AP$ の長さのことだよね」
僕「そりゃわかるよ。おなじみ、三平方の定理だよね。点 $(x_1,y_1)$ と点 $(x_2,y_2)$ の距離を $\ell$ とすると、 $$ \ell = \SQRT{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$ になる。だから、二点の座標値がわかれば、距離もわかる」
二点間の距離
直交座標において、点 $(x_1,y_1)$ と点 $(x_2,y_2)$ の距離を $\ell$ とすると、 $$ \ell = \SQRT{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$ が成り立つ。
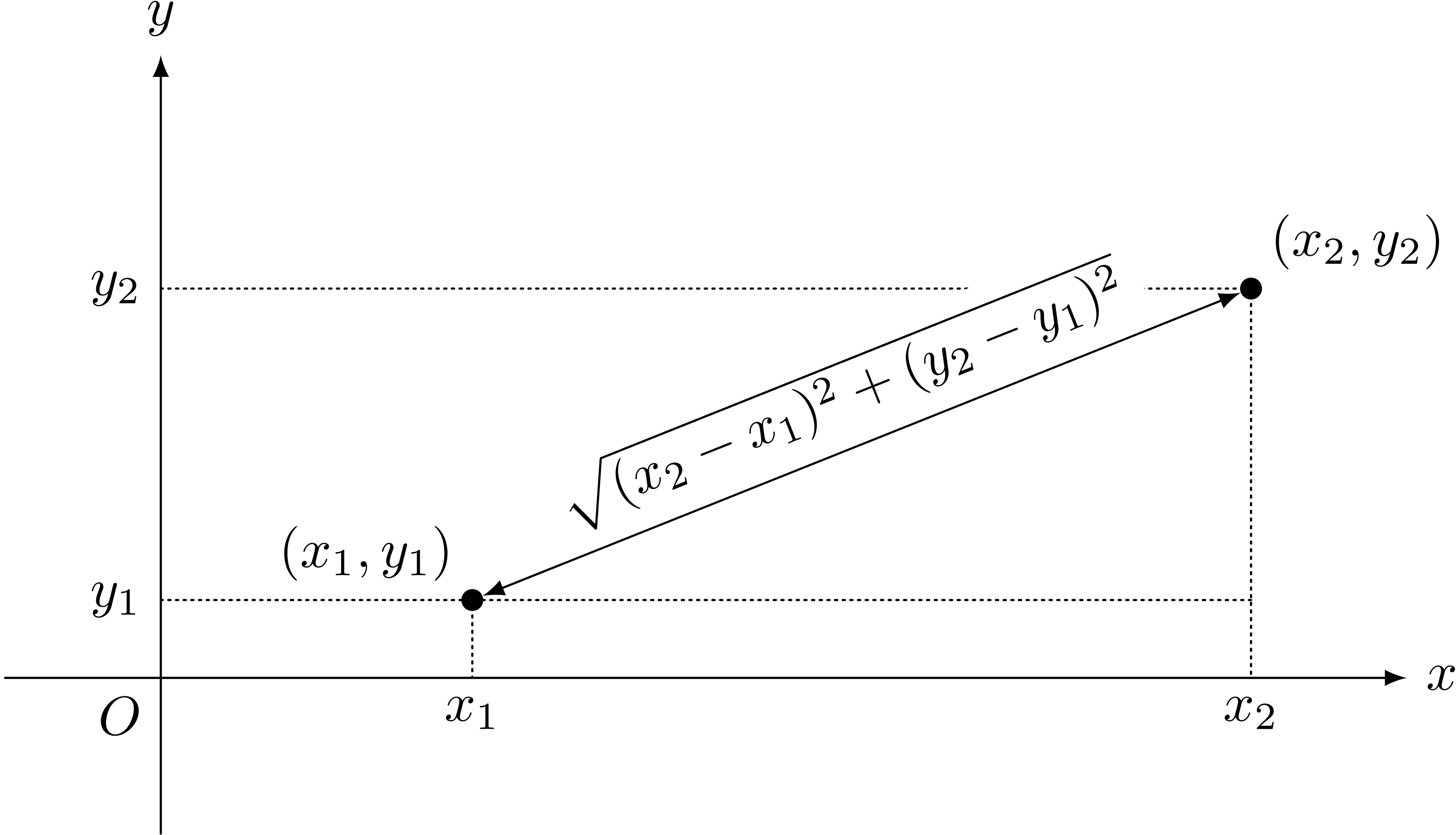
ユーリ「あっ! でもそれは、直交座標じゃん? 花の形はずっと極座標でやってきてたのに、 急に話を変えちゃうわけ?」
僕「ああ、そうだよね。ごめんごめん。僕たちがいま考えていた花の形は、 $$ r = \ABS{\sin\theta} $$ という極方程式だった。ここに出てくる $r$ と $\theta$ の組 $(r, \theta)$ は極座標として考えなくちゃいけない。 でも、僕がいま言った二点間の距離は、直交座標での話。うん、ユーリの言うとおり」
ユーリ「だよねー」
僕「だから、極座標で表した点を直交座標に移し替える必要がある。座標を変換するんだ。 でも、それは、そんなに難しい話じゃない……」
ユーリ「そーなの?」
僕「……うん、すぐわかる。 直交座標を置いておく。 そしてその上に極座標を重ねるように考えるんだ。 ちょうど、グラフ用紙を重ねるみたいに」
直交座標(グラフ用紙のイメージ)

極座標(グラフ用紙のイメージ)
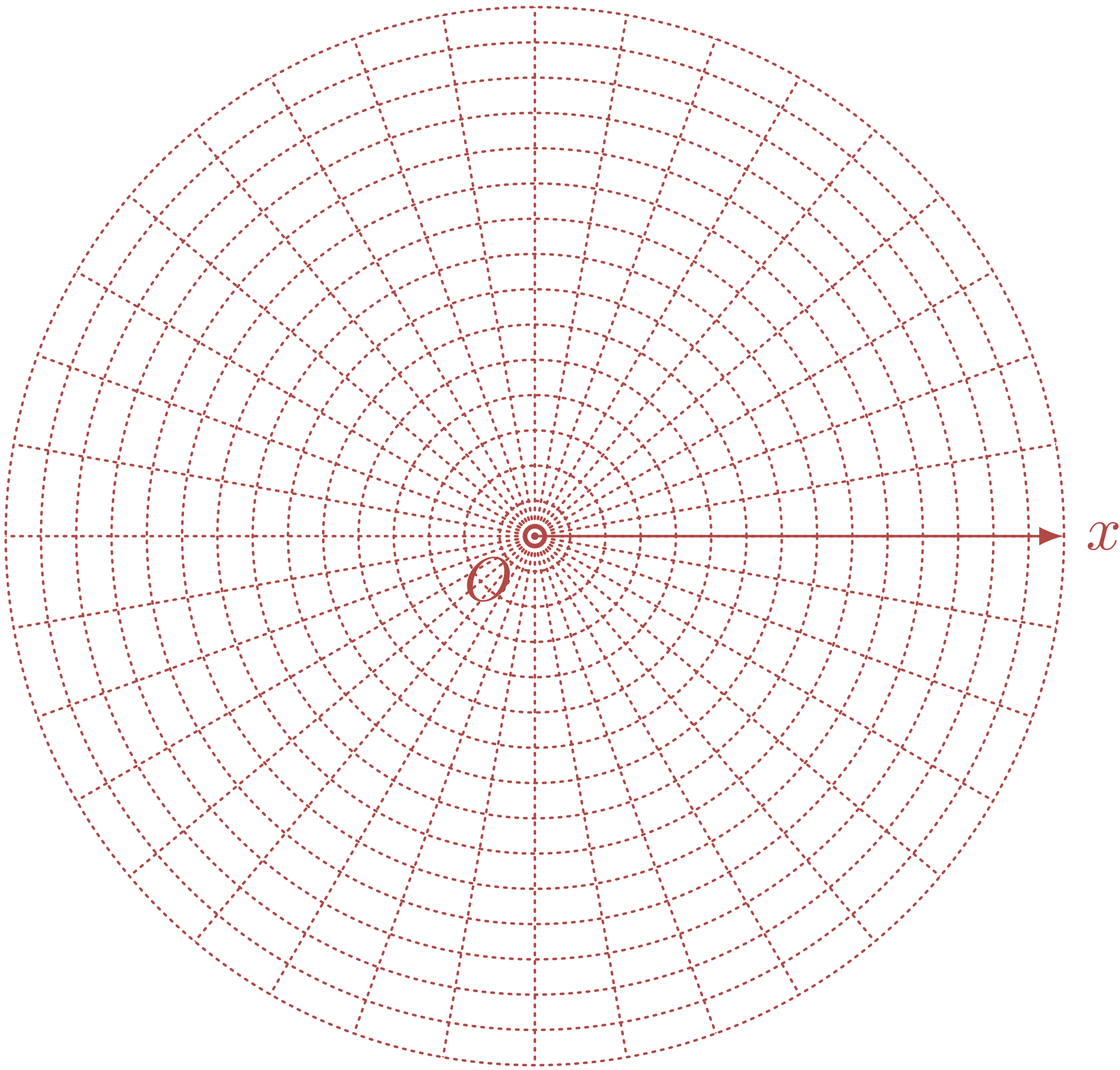
ユーリ「重ねる……?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年8月5日)