![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
双倉図書館(ならびくらとしょかん)で開催されているイベント《いにしえの数学》では、 さまざまな国の、古い時代の数学についてパネルが展示されている。
僕たちはこれまで、 古代エジプトのヒエログリフ(第181回参照)、 古代バビロニアの楔形文字(第183回参照)、 古代ギリシアのタレスとピタゴラス(第185回参照)などの展示を見てきた。 いや、見てきただけじゃない。パネルに示されているクイズにも挑戦してきた。
いま、僕とユーリは、 テトラちゃんといっしょに古代中国の数学テキスト『九章算術』に取り組んでいる。 算木を用いた乗算の問題を考えた後(第188回参照)、 僕たちは正の平方根を求める開平に挑戦しているところ。
『九章算術』巻第四【12】より「平方根を求める」
いま面積が五万五千二百二十五平方歩の正方形がある。 問う、一辺はいくらか。
答、二百三十五歩。
※『科学の名著<2>中国天文学・数学集』より
テトラ「算木でルートの計算をするということですね?」
ユーリ「クイズパネルになってる!」
クイズ(算木で開平を行う)
以下は、算木を使って、 $$ \SQRT{55225} = 235 $$ の計算を行う手順を示している。 ヒントをもとにして、 各手順が何を行っているか、想像してみよう。
(r01)

(r02)
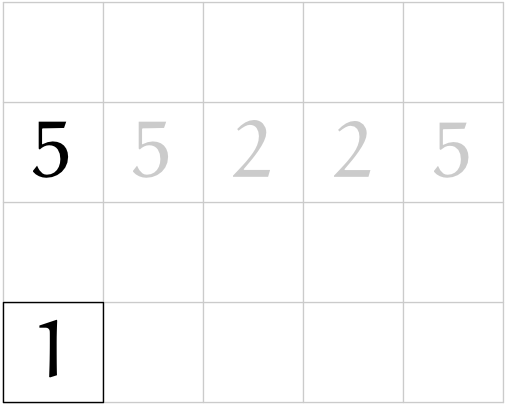
(r03)

(r04)
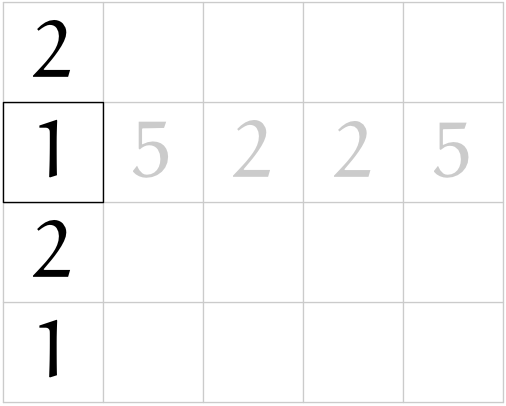
(r05)
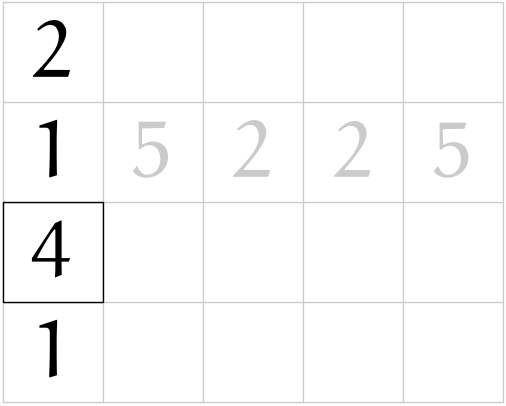
(r06)
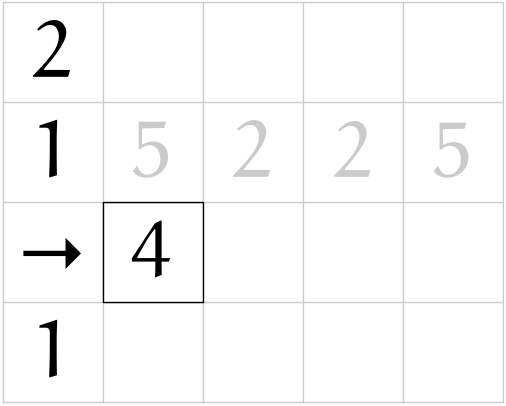
(r07)

(r08)
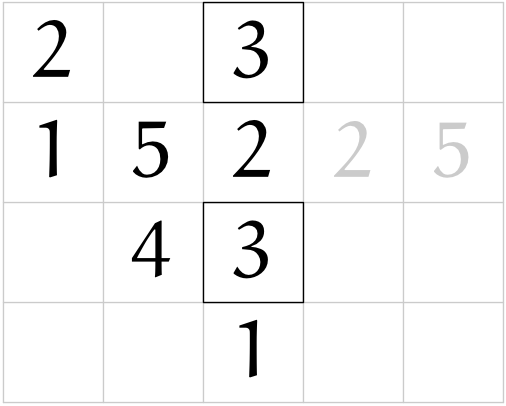
(r09)
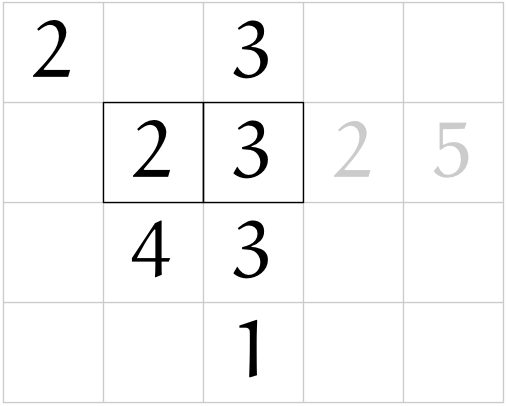
(r10)
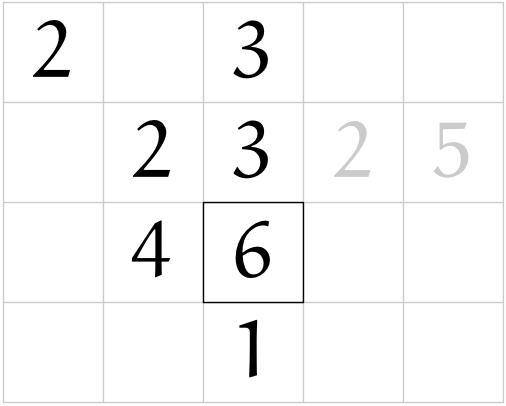
(r11)

(r12)

(r13)
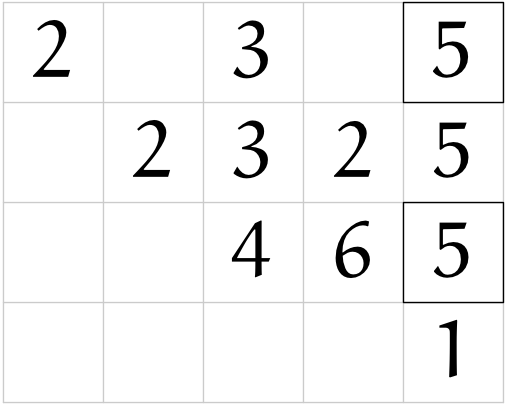
(r14)
(一行目に、 $\SQRT{55225}$ の計算結果である $235$ が得られている)
テトラ「これは、手強そうですね……」
ユーリ「なんでこれで、 $\SQRT{55225}$ が計算できんの?」
僕「それを考えるクイズみたいだよ」
ユーリ「そーなんだけどさー」
テトラ「順番に根気よく読んでいけばきっとわかるはずですよね?」
僕たちは、 算木を使って $\SQRT{55225} = 235$ の計算を行う手順 をいっしょに解読していくことになった。
(r01)

ユーリ「これは、何やってるかわかる!」
テトラ「これからルートを取る数、 $55225$ を算木で並べているわけですね」
僕「そうだろうね。最初に《与えられているものは何か》を明確にしている、と。 ヒントにある $S = 55225$ を使うなら、これから求めるのは $\SQRT{S}$ ということになるね」
(r02)

ユーリ「いっちばん上の位に、 $1$ という印を置きましたー……ってことだね、これ。 ほらほら、乗算のときも上の位から計算したもんね。 ルート取るときも、上の位から調べるんでしょ?」
僕「なるほど。ユーリのいう通りだろうね」
テトラ「あ、あのう……確かに、 算木では上の位から計算をしていましたけれど(第188回参照)、 ここのヒントは《万の位》とわざわざ書いてますよね」
ユーリ「だって、 $55225$ って、いっちばん上の位は《万の位》だよ、テトラさん」
僕「ともかく、先を見てみよう」
(r03)

僕「ようやく計算らしいことが始まったよ。 ここでは、いま注目している $5$ を使って、 $$ 5 \GEQ a^2 $$ を満たす数として $a = 2$ を得たと書いてある。つまり、 $$ 5 \GEQ 2^2 = 4 $$ だから、平方して $5$ 以下になる正整数として $2$ を見つけたわけだ。 これは、要するに $\SQRT{5}$ を推測で求めていることになるんだね」
テトラ「そうですね」
ユーリ「ダウト! $\SQRT{5} = 2.2360679\cdots$ じゃなかったっけ? 《富士山麓オーム鳴く》だし、 $2$ でいーの?」
僕「ああ、もちろん、小数以下は切り捨てたわけだよ。だから、正確には、 $$ \FLOOR{\SQRT{5}} = a \qquad \REMTEXT{$\SQRT{5}$以下の最大整数} $$ となる数として、 $a = 2$ を求めたということだと思うんだけど」
ユーリ「じゃ、このヒントは不正確だね! 『$a = 2$ は、 $5 \GEQ a^2$ を満たす数として得た』じゃなくて、 『$a = 2$ は、 $5 \GEQ a^2$ を満たす最大整数として得た』にしなくちゃ」
僕「確かにそうなるな」
テトラ「ところで、この $a = 2$ という数は、 結局 $55225$ とどういう関係になるんでしょうか」
僕「そうか……うん、それは簡単だよ。 《万の位》に注目して $\SQRT{5}$ を考えるというのは、 結局、 $\SQRT{50000}$ を考えているのと同じこと。 $\SQRT{5}$ の小数以下を切り捨てると $a = 2$ になるというのは、 $$ S \GEQ (100a)^2 $$ という $a$ を求めたことになるね」
ユーリ「$S$ って何だっけ」
僕「数値を具体的に書くと、 $55225$ だよ」
$$ S = 55225 \GEQ 50000 \GEQ 40000 = (200)^2 = (100a)^2 $$テトラ「ははあ……ということは、 $100a = 200$ ですから、 $$ \SQRT{55225} \GEQ 200 $$ という $200$ を見つけたという意味ですね!」
僕「そうなるね。まだ $\SQRT{55225} = 235$ まではたどり着いていなくて、 $200$ というところまで判明したわけだ。 まだ概算ではあるけれど、《百の位》までの詳しさでは正確にわかった、と」
テトラ「はっ! 発見しました!」
僕「何を見つけたの、テトラちゃん?」
テトラ「あのですね。 算木での乗算は上の位から計算したじゃないですか(第188回参照)。 あのときも、最初は概算で、次第に正確になっていきましたねっ!」
僕「なるほど! 確かにそういえるね。算木では $360\times49 = 17836$ を求めるのに、 $$ \begin{align*} \underline{3}00 \times 49 &= 14700 \\ \underline{36}0 \times 49 &= 17640 \\ \underline{364} \times 49 &= 17836 \\ \end{align*} $$ という順になっていったから」
テトラ「そうです、そうです。上の位から計算するので、早い段階から概算が得られています。 でも、筆算では、概算が出てくるのは計算がだいぶ進んでからになりますね」
ユーリ「ねーねー、次を見よーよ」
(r04)

僕「これがよくわからないんだよな」
テトラ「二行目に書いていた $55225$ を $15225$ に書き換えちゃっていますよね。 $5$ が $1$ に変わりました」
ユーリ「$5 - a^2 = 5 - 2^2 = 1$ だから、 $1$ だよ?」
僕「それはわかってるんだけど、その意味がピンと来ないんだ。 $$ R_1 = 5 - a^2 $$ だね」
テトラ「$10000$ 倍して考えますと、 $$ 10000R_1 = 50000 - (100a)^2 $$ ということですね」
僕「そうか。そうだね」
ユーリ「これの意味って何になるの?」
テトラ「$50000$ というのは、 $55225$ を《万の位》までで考えた数ですよね? それから、 $(100a)^2 = 40000$ に出てきた $100a$ というのは、 $\SQRT{50000}$ を《百の位》までで考えた数です。 ということは、 $50000 - (100a)^2$ というのは……なんて言うんでしょうか、ズレの部分ですよね」
ユーリ「ズレ?」
僕「うんうん、誤差かな。 テトラちゃんはいま一万倍して説明してくれたけど、 $5 - a^2$ というのは、 $\SQRT{5}$ を $2$ で近似したときの誤差のようなものだね」
ユーリ「うーん……よくわかんにゃい。 あっ、あっちに説明図のパネルがあるよ! きっとヒントだよ! 見に行こーよ」
僕「えー……見てしまうつもり?」
テトラ「もう少し考えてからにしましょうよ、ユーリちゃん」
ユーリ「総攻撃くらったし」
僕「だからね。まず、僕たちが求めようとしているのは、 $\SQRT{55225}$ なんだけど、それを一気に求めるんじゃなくて、どうやら上の位から求めようとしているらしい。 《百の位》は大小関係で $a = 2$ だとわかった。 $\SQRT{55225}$ は $2XX$ という形らしい。でも、まだ、正確じゃない」
ユーリ「まだ正確じゃないから、ズレを考えるってこと? そっか、ズレの部分も同じように繰り返して調べればいーんだ」
テトラ「あたしもそう思いました。ですから $55225$ を $15225$ にしたのもわかります。 これって、 $5.5225$ から $4.0000$ を引いて $1.5225$ にしたようなものなんですよ」
僕「それはいいんだけど、問題は、同じように繰り返すというのはどういうことか、だと思う」
リサ「正確な繰り返しはアルゴリズムの基本」
僕たちがあれこれ議論しているところに、背後から一言。 びっくりして振り向くと、真っ赤な髪が目立つリサの去りゆく後ろ姿だけが見えた。
ユーリ「あー、驚いた」
(r05)

テトラ「$2$ が $4$ になりました。 $4$ は、 $a$ に $a$ を加えて得た?」
ユーリ「$2 + 2 = 4$」
僕「$a + a = 2a$」
テトラ「$2$ 乗を計算するのに、 $2$ 倍がどう関係するんでしょう」
僕「これだけじゃ、まだわからないなあ。《$2$ 倍の謎》とメモしておくか」
ユーリ「どんどん行こーよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2017年3月10日)