第187回 シーズン19 エピソード7

黄金比の研究

双倉図書館にて

僕「『黄金比はもっとも美しい図形を作る』という話はよく聞くね」

ユーリ「そーなの？　そんなの、数学的に決められるわけないじゃん」

僕「まあまあ。たとえば、縦が $1$ で横が $\phi$（ファイ）の長方形だね。この比率の長方形を黄金長方形と呼ぶ人もいる」

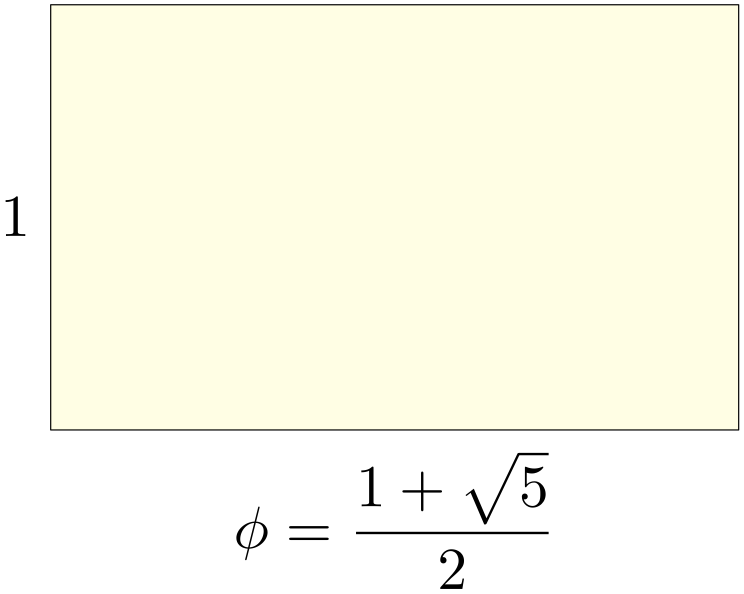
ユーリ「うーん……《もっとも美しい》って決めつけられるの、やだ。 《美しさ》って一つじゃないよ？」

僕「僕もよく知らないけれど、多くの人が美しいと感じるってことかも」

ユーリ「えー、《美しさ》って、多数決で決まるもんなの？」

僕「わかったわかった。数学の話をしようよ。 少なくとも、黄金比にはきれいな関係式が成り立つのはわかるよ。 黄金比 $\phi$ は二次方程式、 $$ x^2 - x - 1 = 0 $$ の解の一つだったから、 $x$ に $\phi$ をあてはめた式、 $$ \phi^2 - \phi - 1 = 0 $$ が成り立つことがわかる」

ユーリ「これがきれいな関係式なの？」

僕「うん。この式から、黄金比のいろんな性質がわかるんだよ。たとえば……」

ユーリ「あー、ちょっと待って待って」

僕「がく。どうした？」

ユーリ「そんなにさっさか話を進めないでよー。 黄金比 $\phi$ って、 $$ \phi = \dfrac{1+\SQRT5}{2} = 1.6180\cdots $$ なわけじゃん？　具体的にわかってるのに、なんでわざわざ二次方程式に話を戻すの？　せっかく、 解の公式で答えが出たのに、なんで話を戻すかなー」

僕「なるほど。なかなか鋭い意見だな、ユーリ。 僕たちはいま、黄金比が持っている性質を研究したいわけだよね」

ユーリ「そだね。《黄金比の研究》かっこいー！　シャーロック・ホームズみたい！」

僕「ホームズは《黄金比の研究》じゃなくて《緋色の研究》だよ」

ユーリ「マジレス、かっこわりー！」

僕「ともかく。 黄金比 $\phi$ の値は $\frac{1+\SQRT5}{2}$ だとわかったし、 小数で表すなら $1.6180\cdots$ になる。 これはもちろんまちがいじゃないし、およその大きさも具体的にわかった。 でもね、十進法を使っているから $1.6180\cdots$ という数字列で黄金比は表せるけど、 僕たちは、何進法とは関係がない、もっと本質的な性質を調べたいわけだよね」

ユーリ「ほほー。そーいえば、バビロニアで $\SQRT2$ を六十進法で書いてたね（第184回参照）」

僕「そうだったね。だから、黄金比を研究するのに、 $1.6180\cdots$ からスタートするんじゃなくて、 黄金比 $\phi$ を生み出した二次方程式 $x^2 - x - 1 = 0$ からスタートするのは、 悪くないと思うよ」

ユーリ「うーん……小数の方はわかったけど、分数の方は？」

僕「分数の方というと？」

ユーリ「あのね、ユーリも $1.6180\cdots$ はどーかと思うの。テンテン（$\cdots$）がついてるし。 でもね、 $$ \phi = \dfrac{1+\SQRT5}{2} $$ からスタートしてもいーんじゃないの？　こっちは正確だよ？」

僕「鋭い。でも、それは同じことなんだ。つまり、 $\phi = \frac{1+\SQRT5}{2}$ からスタートして、 $\phi$ の性質を探っていくと、結局二次方程式が出てくるから」

ユーリ「意味わかんない」

僕「たとえば、こんなふうにね」

$$ \begin{align*} \phi &= \dfrac{1+\SQRT5}{2} && \REMTEXT{黄金比} \\ 2\phi &= 1 + \SQRT5 && \REMTEXT{両辺に$2$を掛けた} \\ 2\phi - 1 &= \SQRT5 && \REMTEXT{$1$を移項した} \\ (2\phi - 1)^2 &= \left(\SQRT5\right)^2 && \REMTEXT{両辺を$2$乗した} \\ 4\phi^2 - 4\phi + 1 &= 5 && \REMTEXT{展開して計算した} \\ 4\phi^2 - 4\phi - 4 &= 0 && \REMTEXT{$5$を移項した} \\ \phi^2 - \phi - 1 &= 0 && \REMTEXT{両辺を$4$で割った} \\ \end{align*} $$

ユーリ「そっか、結局、 $$ \phi^2 - \phi - 1 = 0 $$ が出てくんのか……」

僕「うん、二次方程式とその解っていうのは、お互いにしっかり結びついているからね」

ユーリ「わーった。ちょっと納得。話を先に進めたまえ」

僕「はいはい」

黄金比を研究する

僕「では改めて。黄金比 $\phi$ はこんな関係式を満たしている。 関係式でも、数式でも、等式でも、何と呼んでもいいけどね。 単に式と呼んでもいいよ」

ユーリ「おっけー」

僕「この式を変形させて、 $\phi$ はどんな性質を持つかを研究できる。 式の形を観察することでね」

ユーリ「出たな《数式マニア》」

僕「どんな風に変形させても発見はあると思うけど、たとえば、こんなふうにしてみよう」

$$ \begin{align*} \phi^2 - \phi - 1 &= 0 && \REMTEXT{黄金比の関係式} \\ \phi^2 &= \phi + 1 && \REMTEXT{$\phi + 1$を移項} \\ \end{align*} $$

ユーリ「これを観察すると、何がわかるの？　じー」

$$ \phi^2 = \phi + 1 $$

僕「《黄金比を $2$ 乗した数は、黄金比に $1$ 足した数に等しい》ことがわかる」

ユーリ「あたりまえじゃん。式を見ればわかるもん」

僕「そうそう、式を見ればわかるよね。もちろん、実際に計算してもそうなってる」

$$ \begin{align*} \phi^2 &= \left(\dfrac{1+\SQRT5}{2}\right)^2 && \REMTEXT{黄金比を$2$乗} \\ &= \dfrac{\left(1+\SQRT5\right)^2}{4} && \REMTEXT{分母を計算} \\ &= \dfrac{1^2 + 2\SQRT5 + \left(\SQRT5\right)^2}{4} && \REMTEXT{分子を計算}\\ &= \dfrac{6 + 2\SQRT5}{4} \\ &= \dfrac{3 + \SQRT5}{2} && \REMTEXT{$2$で約分} \\ &= \dfrac{2 + 1 + \SQRT5}{2} && \REMTEXT{分子を和に分けて黄金比を作っていく} \\ &= \dfrac{2}{2} + \dfrac{1+\SQRT5}{2} && \REMTEXT{分解した} \\ &= 1 + \dfrac{1+\SQRT5}{2} && \REMTEXT{$\frac22 = 1$だから} \\ &= \dfrac{1+\SQRT5}{2} + 1 \\ &= \phi + 1 \\ \end{align*} $$

ユーリ「ふむふむ。確かに、 $$ \phi^2 = \phi + 1 $$ になってるってことね」

僕「もうちょっと変形してみようか。 $\phi$ について知りたいんだから、 $\phi = \cdots$ という形になるように、 両辺を $\phi$ で割ってみるよ。もちろん $\phi \neq 0$ だからゼロ割にはならない」

$$ \begin{align*} \phi^2 &= \phi + 1 && \REMTEXT{上の式から} \\ \phi &= \dfrac{\phi + 1}{\phi} && \REMTEXT{両辺を$\phi$で割った} \\ \end{align*} $$

ユーリ「《黄金比は、黄金比に $1$ 足した数を黄金比で割った数に等しい》……ってこと？」

僕「その通りだね。式を見ればそう書いてある」

ユーリ「……」

僕「ではさらにこんなふうに変形しよう」

$$ \begin{align*} \phi &= \dfrac{\phi + 1}{\phi} && \REMTEXT{上の式から} \\ \phi &= \dfrac{\phi}{\phi} + \dfrac{1}{\phi} && \REMTEXT{分解} \\ \phi &= 1 + \dfrac{1}{\phi} \\ \end{align*} $$

ユーリ「ほほー。《黄金比は、 $1$ に黄金比の逆数を加えた数に等しい》？」

僕「その通り。式を見ればわかる」

ユーリ「見ればわかるけど、つまんない」

僕「つまんない？」

ユーリ「つまんない。だって、あたりまえだし。もともと《美しい》かどーかって話じゃなかったっけ？　別に、美しくないよ？」

僕「ともかく、この式をよく見てみよう」

$$ \phi = 1 + \dfrac{1}{\phi} $$

ユーリ「じー」

僕「左辺に一つ $\phi$ があって、右辺にも一つ $\phi$ がある。この $\phi$ は同じ数を表しているよね」

ユーリ「そだね。黄金比」

僕「この式の《右辺全体》は $\phi$ に等しいんだから、《右辺の $\phi$》を《右辺全体》で置き換えてもいいよね！　 つまり、 $\phi$ をすぽっと $1+\frac{1}{\phi}$ で置き換えるんだよ」

$$ \begin{align*} \phi &= 1 + \dfrac{1}{\phi} && \REMTEXT{上の式から} \\ \phi &= 1 + \dfrac{1}{1 + \dfrac{1}{\phi}} && \REMTEXT{右辺の$\phi$を$1 + \frac{1}{\phi}$で置き換えた} \\ \end{align*} $$

ユーリ「えっ？　う、うーん……ま、まーね。それはそーか」

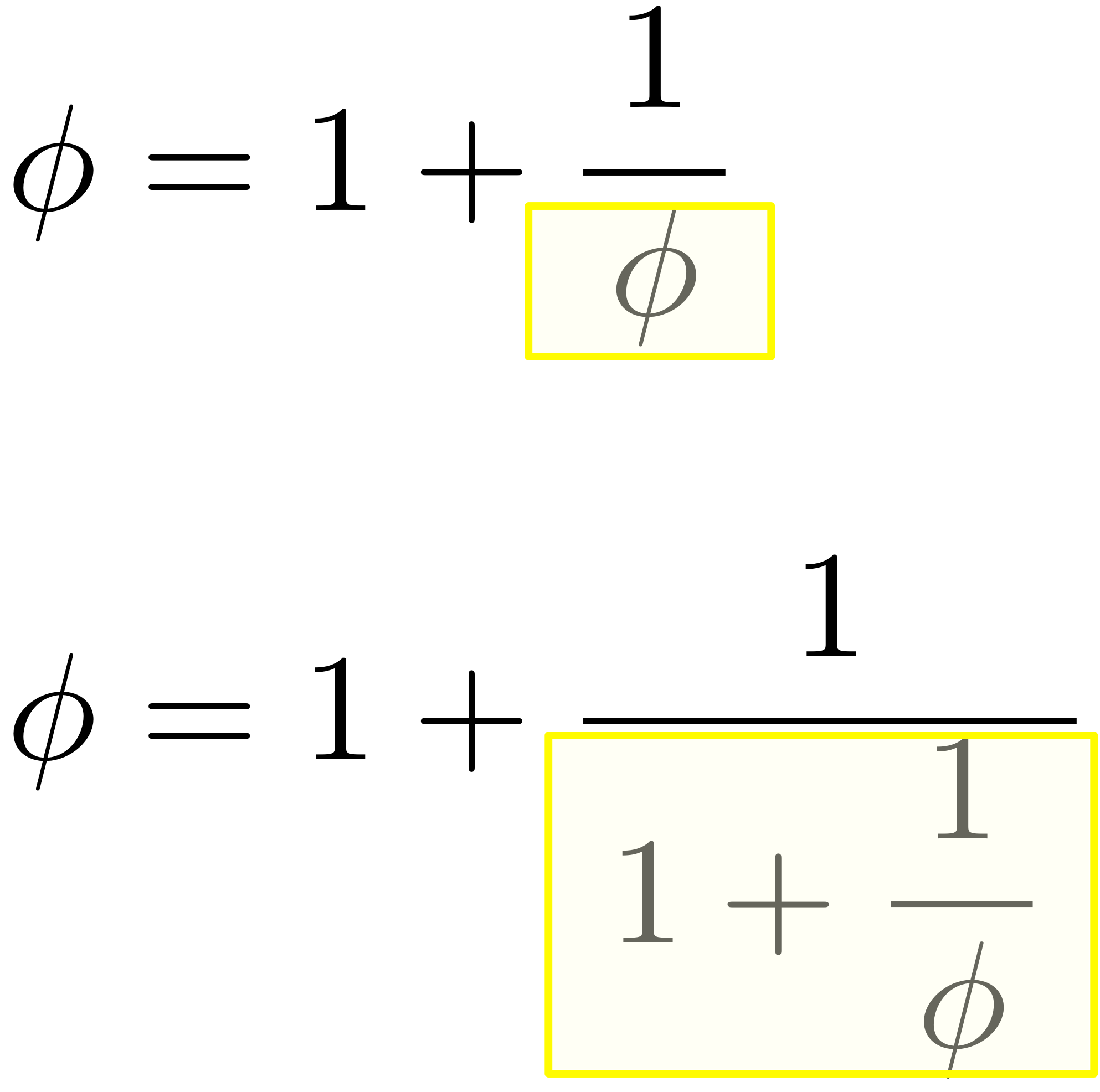
僕「そして、まだ右辺に一つ $\phi$ がある。それもまた、 $1+\frac{1}{\phi}$ で置き換えることができる」

$$ \begin{align*} \phi &= 1 + \dfrac{1}{1 + \dfrac{1}{\phi}} && \REMTEXT{上の式から} \\ \phi &= 1 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{\phi}}} && \REMTEXT{右辺の$\phi$を$1 + \frac{1}{\phi}$で置き換えた} \\ \end{align*} $$

ユーリ「うわあ……お兄ちゃん、これって、もしかして、無限に続く？！」

僕「そうなるね。これは、黄金比の連分数による表示だよ」

ユーリ「れんぶんすう」

ユーリ「おもしろーい！　こーゆー式は《美しい》かも！」

僕「だよね！　数式を変形させて、その式の形をじっと眺めるとおもしろいことがわかるんだよ」

ユーリ「他には？　ねー、おもしろいこと、もっとないの？」

黄金比の逆数を研究する

僕「さっきは $\phi = \cdots$ という形にして考えたけど、今度は $\frac{1}{\phi} = \cdots$ という形にしてみようか」

ユーリ「わくわく」

$$ \begin{align*} \phi &= 1 + \dfrac{1}{\phi} && \REMTEXT{黄金比の関係式から得た式} \\ \phi - 1 &= \dfrac{1}{\phi} && \REMTEXT{$1$を移項} \\ \dfrac{1}{\phi} &= \phi - 1 && \REMTEXT{両辺を交換した} \\ \end{align*} $$

僕「ユーリなら、黄金比の関係式から導いた、 $$ \dfrac{1}{\phi} = \phi - 1 $$ という式をどう読む？」

ユーリ「これって《黄金比の逆数は、黄金比から $1$ 引いた数に等しい》ってことだよね」

$$ \dfrac{1}{\phi} = \phi - 1 $$

僕「そうだね」

ユーリ「ここから、なんか、おもしろいこと言えないか……」

僕「そうそう」

ユーリ「うーん……あんまりわかんにゃい。お兄ちゃんなら？」

僕「もちろん、いろんな読み方があるけど、さらに両辺を変形させてみようか……こんなふうに」

$$ \begin{align*} \dfrac{1}{\phi} &= \phi - 1 && \REMTEXT{上の式から} \\ \dfrac{1}{\phi} &= \dfrac{\phi - 1}{1} && \REMTEXT{$\phi - 1$を$1$で割った} \\ \end{align*} $$

ユーリ「は？　 $1$ 分の $\phi - 1$ って？　分母が $1$ なんて無意味じゃん」

僕「ともかく、式を読もう。この式は成り立つよね？」

$$ \dfrac{1}{\phi} = \dfrac{\phi - 1}{1} $$

ユーリ「成り立つけど、そーする意味がわかんないの！」

僕「分数の形で書いてみると、《比の値》に見えてくる。 つまり、 $$ \dfrac{1}{\phi} = \dfrac{\phi - 1}{1} $$ ってことは、 $$ 1:\phi = (\phi - 1):1 $$ が成り立つってこと」

ユーリ「はあ。そんで？」

僕「ついさっき、出てきたよね。 $1:\phi$ という比の話題が」

ユーリ「$1:\phi$ って……黄金長方形だ！」

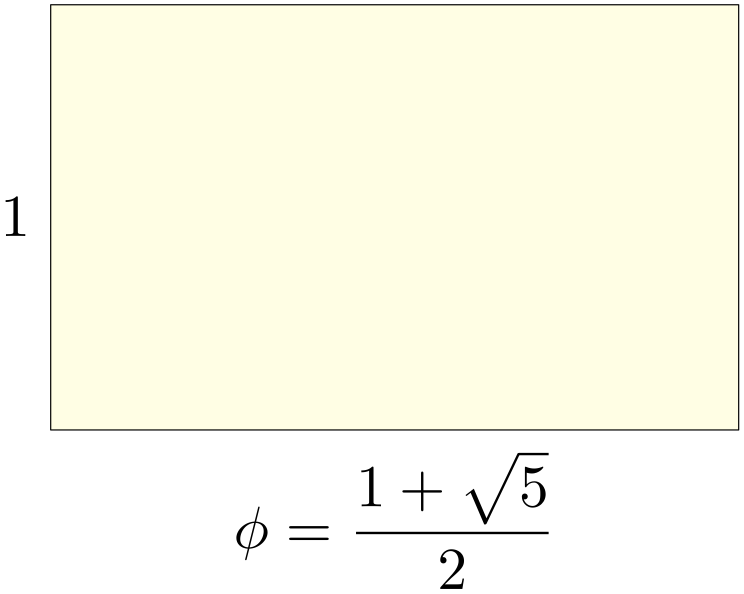
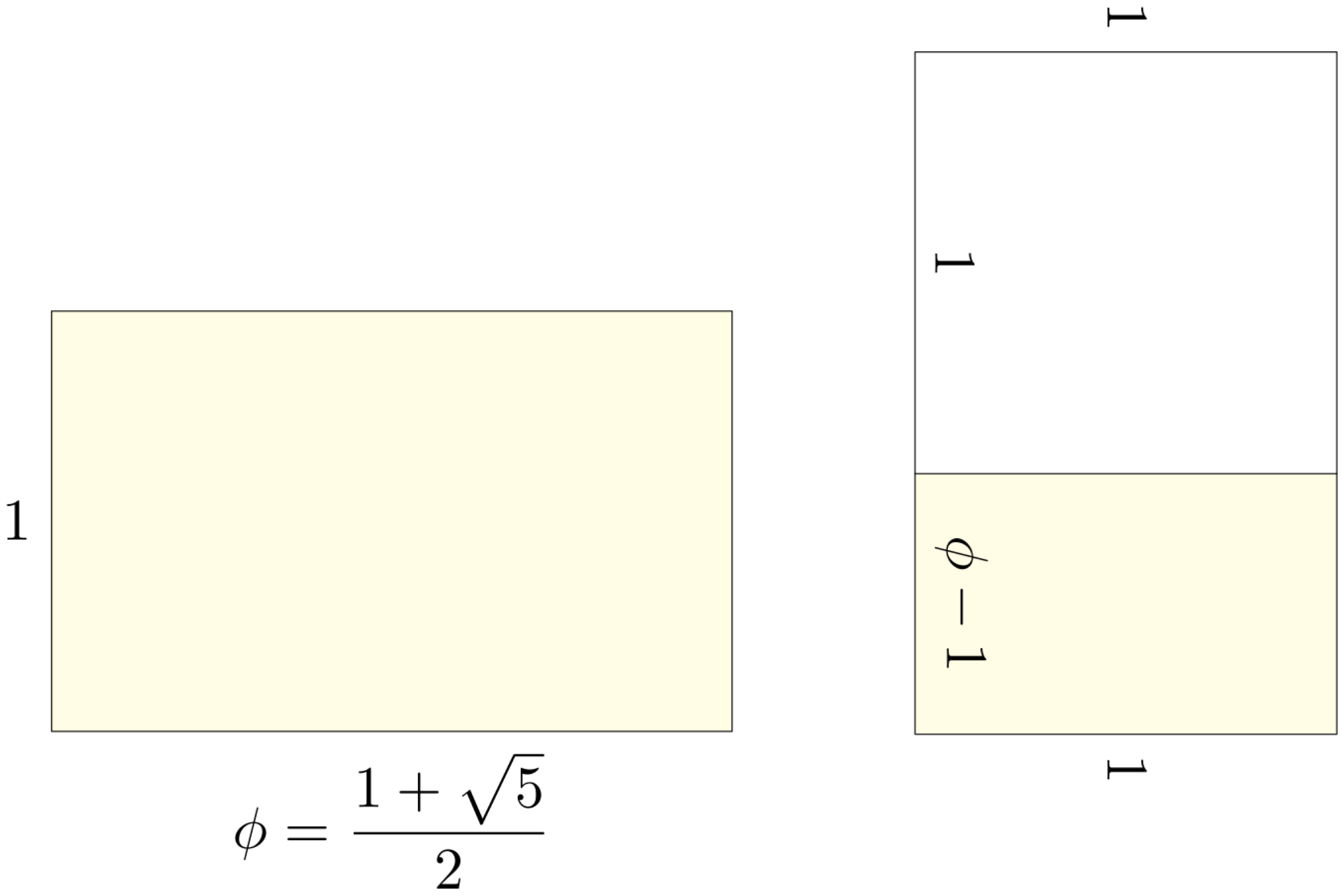
僕「そうだね。 $1:\phi$ に出てきた $1$ と $\phi$ が、黄金長方形の二辺に見えてきた。 では、 $(\phi-1):1$ に出てきた $\phi-1$ と $1$ は、どんな長方形を作るかな？」

ユーリ「待って待って。ユーリ、わかる！　 $\phi-1$ って $\phi$ から $1$ を引くから、 横から縦を引いた分だよね？　だから、これ！　こんな長方形！」

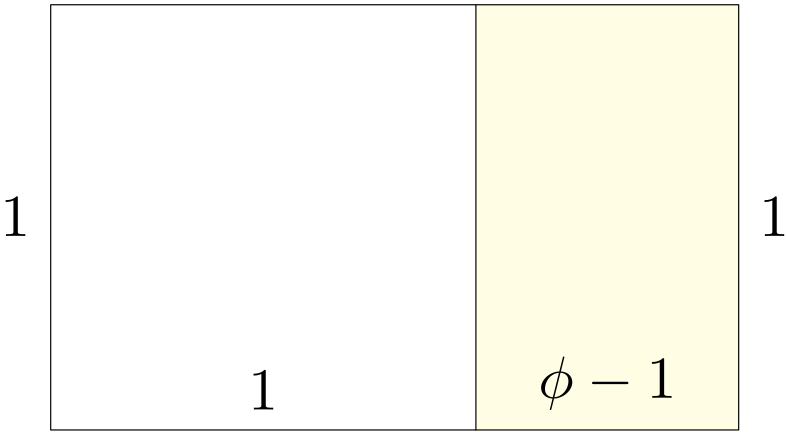
僕「そうだね。黄金長方形の《短い辺》が一辺となる正方形を切り取った残りの長方形になる」

ユーリ「……てことは、ねー、お兄ちゃん、お兄ちゃん！　もしかして、 その長方形も《黄金長方形》じゃないの？」

僕「その通り！　僕たちが導いた、 $$ 1:\phi = (\phi - 1):1 $$ は、そのことを主張しているね。残りの長方形の二辺の比は $1:\phi$ に等しいわけだから。 大きな黄金長方形の《短い辺》が、小さな黄金長方形の《長い辺》になる。 正方形を切り取るごとに、黄金長方形が生まれるんだね！」

ユーリ「なにそれすごいじゃん！　おもしろいにゃあ……」

僕「おもしろいよね。正方形を切り取った残りもまた黄金長方形になる。 つまり、全体の長方形と残りの長方形は、相似になるということ。 これは黄金比の《美しい》性質だと思うよ。 黄金長方形が見た目に美しいかどうかはさておいて、 黄金比はこういう《その値でなければ得られない性質》を持っているよね。 僕はその《ゆるぎない》ところが美しいと思うんだけどな……その値でしか、その性質は持ち得ない」

ユーリ「はっ、もしかして！　こういう長方形って、かならず $1:\phi$ になるのっ？」

僕「もちろん。短い辺を一辺にする正方形を切り取った残りの長方形が、もとの長方形と相似になるとき、 その長方形は黄金長方形になるね」

ユーリ「うわー……あっ、これ、無限に続く！　続けられる！」

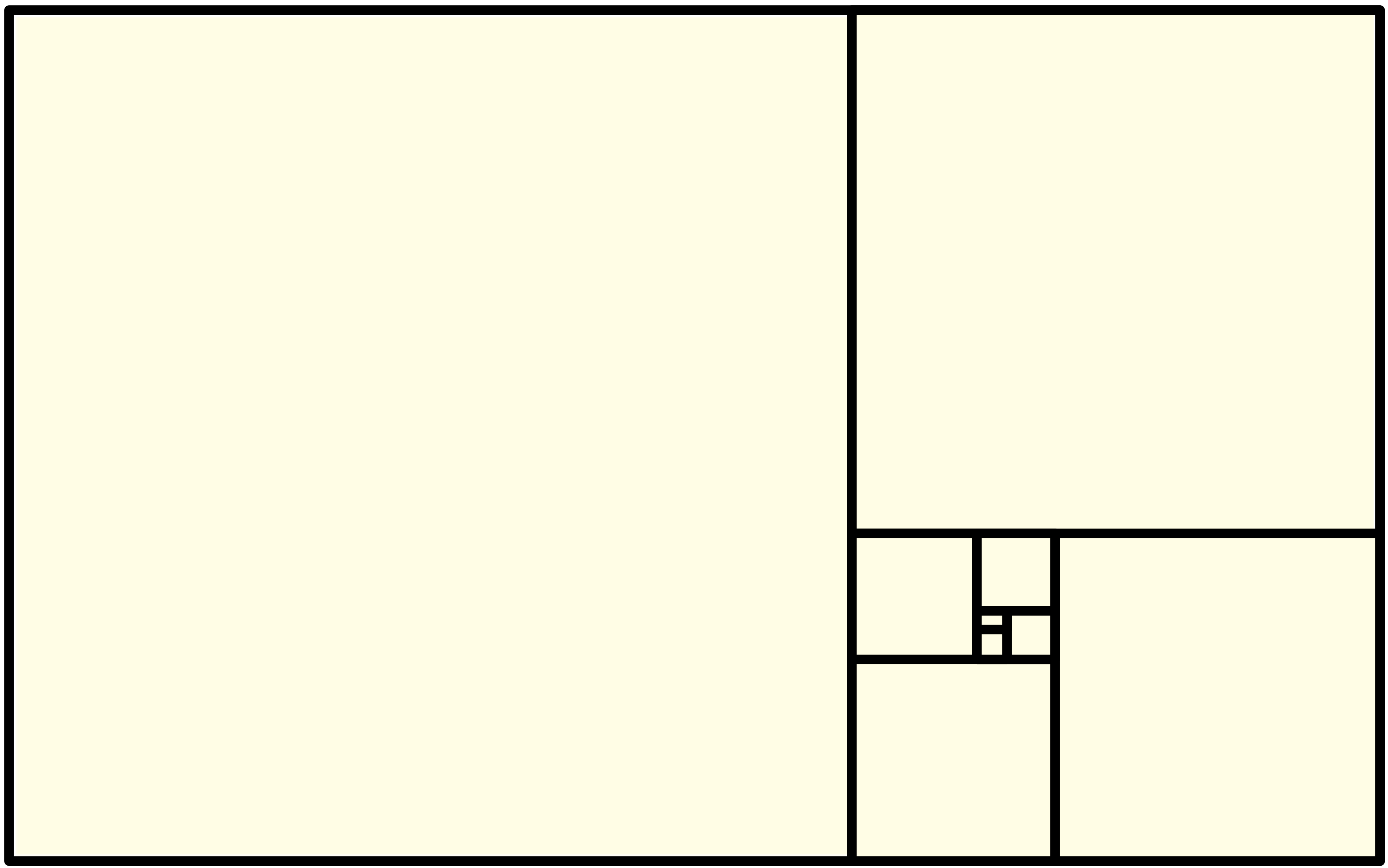
僕「そうだね。正方形を切り取り、残った長方形から正方形を切り取り……って、無限に続けられる」

ユーリ「おんなじ形が無限に続く……」

僕「小さくなっていくけれど、すべての長方形は相似になるね」

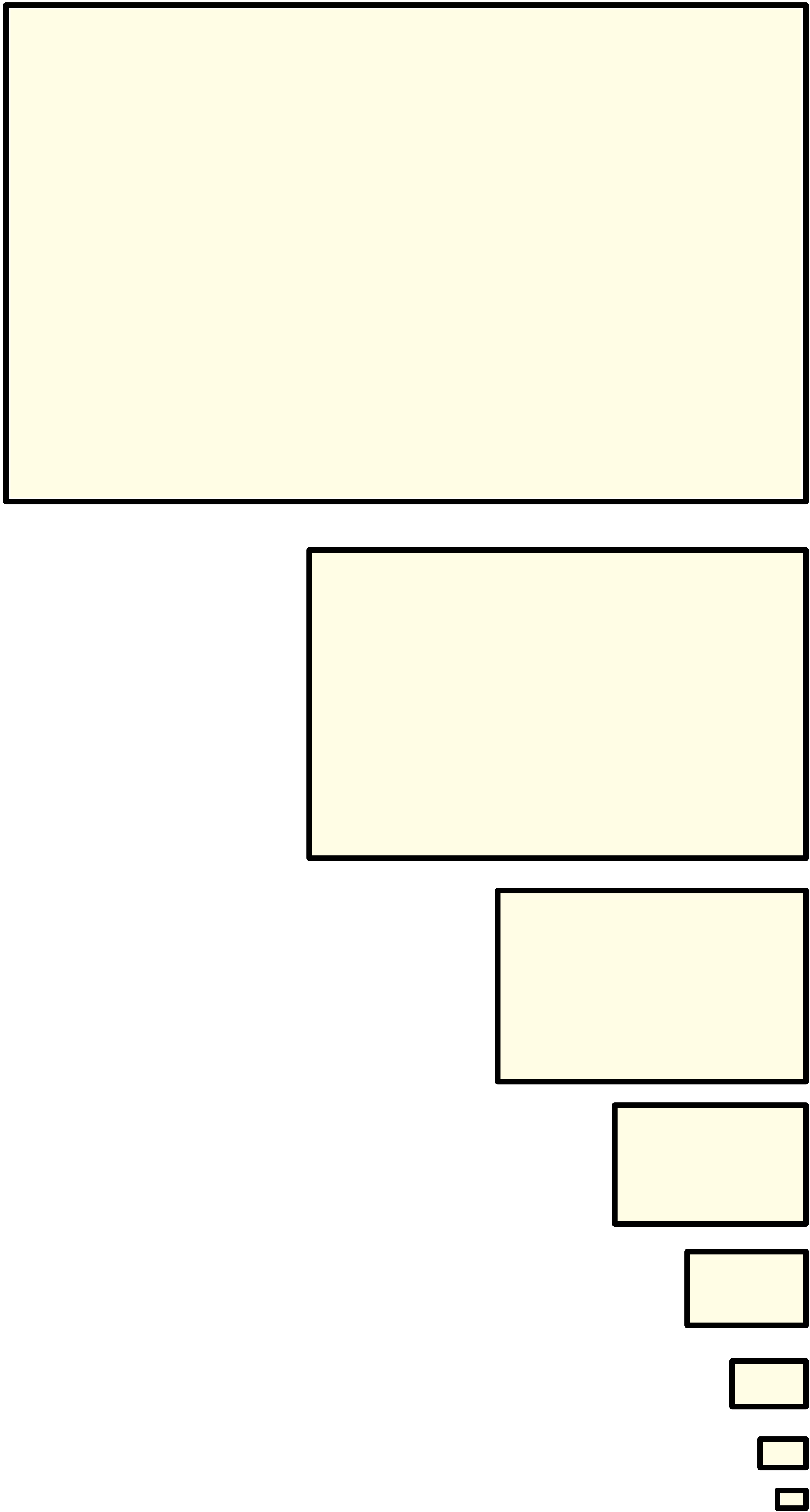
ユーリ「……」

黄金比の冪乗を研究する

僕「じゃ、次は、とっておきの話をしよう」

ユーリ「わくわく！　また、黄金比の関係式からスタート？」

僕「もちろん。この話は、以前ミルカさんといっしょに考えていたことなんだ」

ユーリ「ミルカさまと？」