第186回 シーズン19 エピソード6

古代ギリシアの数学（後編）

双倉図書館にて

ユーリ「《共通の尺度》の話はおもしろかったねー。じゃっ、次のパネルに行ってみよー！」

僕「こっちもピタゴラスの話だな……『プロクロスは、おそらくエウデモスからの引用であろうが、 次の二つの数学上の発見をピタゴラスに帰していた。 それらは（１）正多面体の作図、（２）比例の理論である。 これをどの程度文字どおりに受け取ってよいものかどうかは疑問だが、 この言明がピタゴラス学派の思想の方向を正しく反映している可能性は十分に考えられる……』と。ボイヤー『数学の歴史』より、とのこと」

ユーリ「プロクロスとかエウデモスとかピタゴラスとか、 名前いっぱい出てきた。プロクロス is 誰」

僕「ほら、 ピタゴラスが書いたものは残っていないってパネルがさっきあったよね。あそこに出てきた人だ。 プロクロスは、エウデモスの数学史の要約を、ユークリッドの原論の第一巻の注釈の中に組み込んで書いた人」

ユーリ「あー、ま、いっか。それはさておき」

僕「さておくなよ」

ユーリ「こっちのパネルにクイズがあるよ。比例の理論、だって！」

ユーリ「なにこれ」

僕「なるほど、《$b-a$ と $c-b$》の比の値が、 《$a$ と $a$》《$a$ と $b$》《$a$ と $c$》の比の値でそれぞれ表される関係を調べよということか……」

ユーリ「そんなの、考えたことないよー」

僕「だから、いま考えるんだよ、ユーリ」

僕「……」

ユーリ「あっ、お兄ちゃん。抜け駆け禁止！　式の計算始めてるね！」

僕「いやいや、抜け駆けとかそういうんじゃなくてね。僕たちには（１）の式が与えられている」

僕「これを《$b$ を定義している式》だと考えるんだから、 $$ b = \cdots $$ という形になるように変形すればいいはず。さて……なるほどなるほど」

ユーリ「ちょっと待ってよー……ユーリも、すぐ計算するから」

僕「……できた？」

ユーリ「……できた！　（１）は、こーでしょ？」

僕「そうだね。（１）の関係式は、 $$ b = \dfrac{a + c}{2} $$ になった。だから？」

ユーリ「だから、（１）で定義されている $b$ は《$a$ と $c$ の平均》なんだ！　楽勝楽勝」

僕「そう、それでいいはず。 $a$ と $c$ を足し合わせて、 $2$ で割っているから、平均になる。 より正確には算術平均（さんじゅつへいきん）になるね」

ユーリ「じゃっ、次は（２）やるねー。これも $b = \cdots$ にすればいーんでしょ？」

僕「……」

ユーリ「……できた、けど？」

僕「うんうん。（２）は、 $$ b = \SQRT{ac} $$ になったね。そうだろうと思ったよ」

ユーリ「うわなにその発言。 $a$ と $c$ を掛けて、ルート取ったものが $b$ って……計算はできたけど、 これって何がおもしろいの？」

僕「さっきの（１）は算術平均だったけど、この（２）は幾何平均（きかへいきん）だよ。 $\SQRT{ac}$ は $a$ と $c$ の幾何平均。 これも平均の一種」

ユーリ「えっ、だって掛け算だよ？　足してないよ？　それなのに平均なの？」

僕「そうだね。ほら、平均っていうのは、複数の数を《平らに均す（ならす）》のが目的だから、 その均し方にはいろいろあるんだよ。 もちろん、普通に平均といったら算術平均のことになるけどね。 幾何平均も対数取れば算術平均だし」

ユーリ「掛け算してルート取るのが均している……さっぱりわからへん」

僕「なぜ急にあやしい関西弁になる。 じゃ、《平らに均す》というのを、こんなふうに考えてみようよ。 算術平均は $a$ と $c$ を足して $2$ で割った。 ロープを一本釘に引っ掛けたとき、 ぶらさがっている長さが $a$ と $c$ のようにアンバランスだとする」

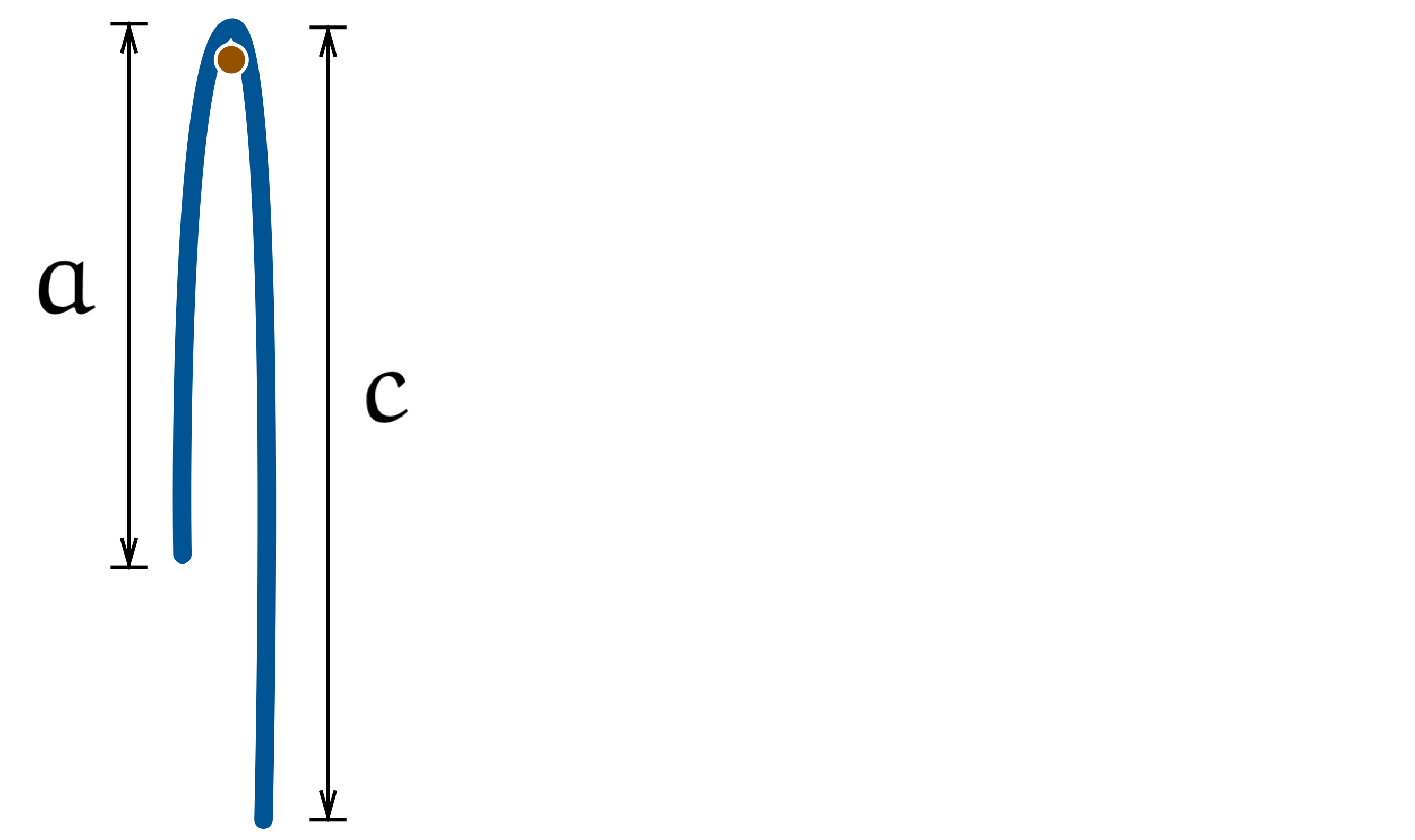
ユーリ「ロープ？」

僕「そう。ロープの長さはもちろん $a+c$ だよ。 そして、ロープを引っ張ってバランスを取った。 そのとき、ぶらさがっている長さは $\frac{a+c}{2}$ になる」

ユーリ「ほほー」

僕「言い換えると、二つの長さの和が一定という条件を付けて、 $2$ 本の長さを揃えたわけだね。これが算術平均の均し方」

ユーリ「確かに！　おもしろーい！」

僕「それに対して、幾何平均では $a$ と $c$ を掛けてルートを取る。 それはね、縦と横の長さが違う長方形があったとして、 その縦と横の積が一定という条件を付けて、 縦と横の長さを揃えたことになるんだ」

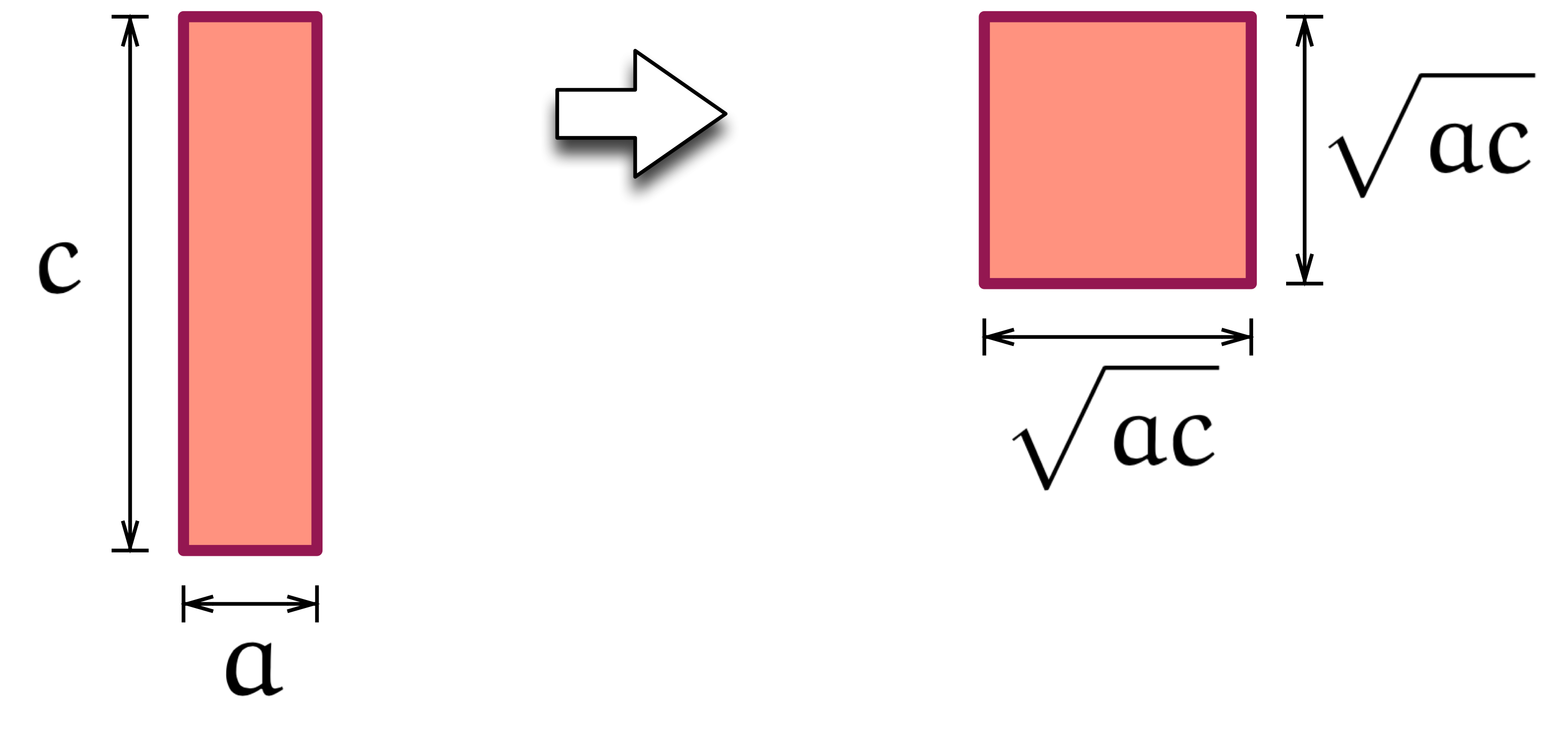
ユーリ「おー、そっか！　長方形と面積がおんなじ正方形を作ったってこと？」

僕「$2$ 個の数の幾何平均だと、そうなるね。 $b^2 = ac$ という式をよく見ると、 そのことがよくわかる。 『《二辺が $a$ と $c$ である長方形の面積》と等しい正方形の一辺は $b$ だ』と言ってるわけだから」

ユーリ「何だか、平均っぽく見えてきた！」

僕「最後は（３）の式だね」

ユーリ「待って待って待って。ユーリが計算するから。お兄ちゃんはそのまま、動かないで！」

僕「さてと。（３）から、 $$ b = \dfrac{2ac}{a + c} $$ という式が出てきたわけだけど」

ユーリ「今度は足し算と掛け算が混ざってる……これも、平均？　平均っぽくないよ？」

僕「これは、もう少し式変形をしないと、平均には見えないよ」

ユーリ「お兄ちゃんは《数式マニア》だから……いや、待って、ユーリもできるかも。だって、隠れてるもん」

僕「隠れてる？」

ユーリ「あのね、さんじゅちゅ……さんずちゅ……算術平均が隠れてるの。ここに！」

僕「ほほう！」

ユーリ「$\frac{a+c}{2}$ の、逆数の逆数だと考えたの！　逆数が隠れてたんだよー！　 $ac$ の方はわかんなかったケド」

僕「逆数までたどり着いたんだ、すごいな！」

ユーリ「こっから、どーすんの？」

僕「うん、こんな式変形をすると、見えてくるよ」

ユーリ「逆数の逆数……」

僕「そうだね。《《$a$ の逆数》と《$c$ の逆数》の算術平均》の逆数。これは調和平均（ちょうわへいきん）というよ」

ユーリ「へー……」

僕「比の値と平均が関わるって、考えたことなかったよ。 もしかしたら《共通の尺度》について考えるというのと、 比について考えるというのは関連しているんだろうか」

ユーリ「……」

僕「で、ユーリは何を考えているのかな」

ユーリ「……お兄ちゃん、これって階差数列みたいだね」

僕「おっと？」

ユーリ「《$a,b,c$》と《$b-a,c-b$》の関係って、 数列と階差数列の関係じゃん？

僕「なるほど、確かに。ということは、（１）の式を解読すると《階差数列の比が一定》、 （２）の式は《階差数列の比がもとの数列の第 $1$ 項と第 $2$ 項の比に等しい》、 （３）の式は《階差数列の比がもとの数列の第 $1$ 項と第 $3$ 項の比に等しい》といえる……」

ユーリ「ふむー……」