![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
今日は土曜日。ここは僕の家。 いとこのユーリと僕はダイニングで、母さんが作ったスパゲティを食べている。
僕「ユーリ、何見てるんだ?」
ユーリはさっきから皿をじっと見つめている。
ユーリ「ねーお兄ちゃん。これって楕円?」
僕「何のこと?」
ユーリ「このソーセージ」
ユーリはスパゲティに入っていた小さな輪切りのソーセージをフォークの先でつついた。
僕「ああ、そうだね。ソーセージを円筒だと思って、 ナイフを平面だと思えば、断面は楕円になるよ。 切ったあとで炒めるから変形しちゃうけどね」
僕はそばにあった紙に、円筒を平面で切る図を描いた。
円筒を平面で切る
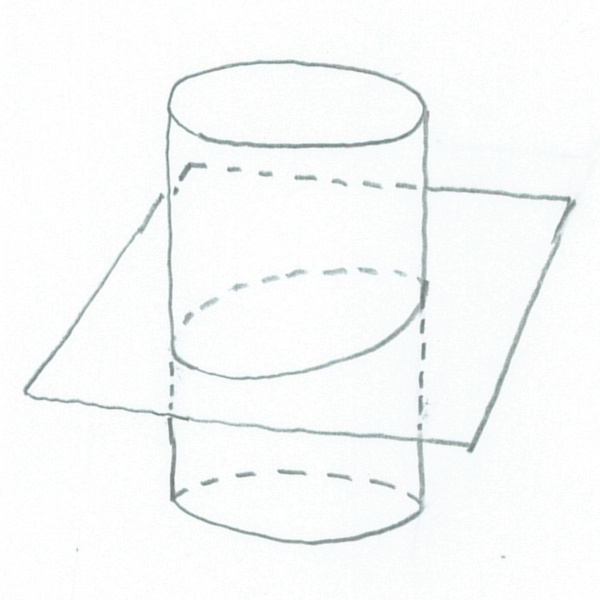
ユーリ「お兄ちゃん、図うまいね! ちょっとゆがんでるけど」
僕「ミルカさんみたいなツッコミどうも。 ソーセージみたいな中身が詰まったものだと、 円筒というより円柱といったほうがいいかな。 まあ、形に注目するだけなら円筒でかまわないけど」
ユーリ「ほら、こないだ《ささやきの回廊》のこと教えてくれたじゃん?(第84回参照) あれから、楕円が気になって気になって……」
僕「大げさ」
ユーリ「へへ。てゆーかさ……《焦点から焦点へないしょ話が伝わる》って、お兄ちゃんが証明してくれたじゃん? あれ、けっこー感動もんだったから」
僕「それはそれは」
母「どう? 感想が聞こえてこないけど、おいしいかしら?」
ユーリ「はーい、とってもおいしいです」
母「よかった。あなたは?」
僕「まあ、おいしいけど」
母「けど?」
僕「おいしいよ……ごちそうさま」
ユーリ「あっ、ちょっと待ってお兄ちゃん。ユーリもすぐ食べ終わるから!」
ユーリ「早くやってよ!」
僕「何を?」
ユーリ「さっきの、証明して! ソーセージの楕円問題」
僕「え、あの話まだ続くのか」
ユーリ「《円筒を平面で切ると、断面が楕円になることを証明せよ》…… ほら、入試にもきっと出るよ! この問題」
僕「出ない出ない。それに断面は楕円になるとは限らないし」
ユーリ「え?」
僕「こんなふうに、水平に切ったら断面は円だろ?」
円筒を水平に切った断面は円
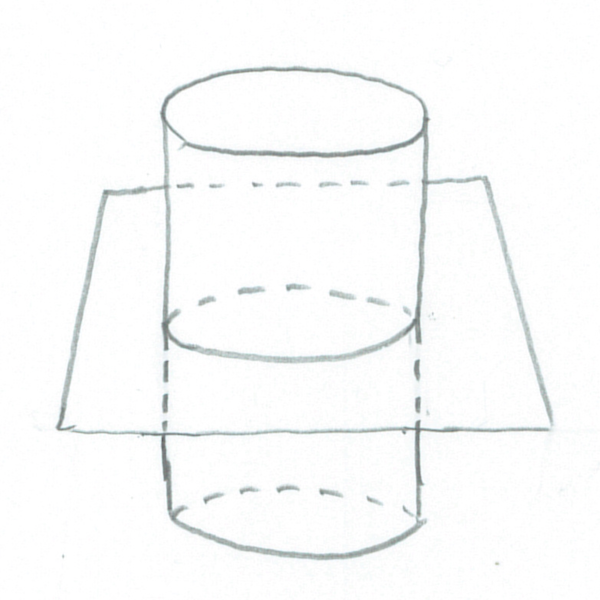
ユーリ「それは、お兄ちゃんにしては甘い主張だにゃ。 円は楕円の特別な場合でしょ! 円も楕円の仲間なんだから、 断面が楕円って言ってもいーじゃん」
僕「さすがにユーリはだまされないか……いや、 やっぱりちがうな。円筒を平面で切ったときに断面が(円を含む)楕円にならない場合はあるよ」
ユーリ「え!」
僕「わかるかにゃ……」
ユーリ「ユーリのマネするなー! ……ほんとに?」
僕「ほんとほんと」
ユーリ「……わかった。あれでしょ? ソーセージを横や斜めに切るんじゃなくて、まっすぐ縦に切る。そうしたら断面は……直線?」
僕「そうだね。 円筒を、その中心軸に平行な平面で切った場合、 普通は直線が $2$ 本になる。 ぎりぎりソーセージに接するようにナイフを使えば、直線は $1$ 本。 まあ接する場合を切断といえるかどうかは微妙だけどね」
ユーリ「そんじゃ、条件付け加えて、こーゆー問題にする! 《円筒を、中心軸に対して斜めの平面で切った場合、断面が楕円になることを証明せよ》……これなら文句ないでしょ?」
僕「……しょうがないなあ。 じゃ、いっしょに考えてみようか」
ユーリ「うん!」
読者さんへ
ここで先に進むのをちょっとストップしてください。
ユーリの問題、
《円筒を、中心軸に対して斜めの平面で切った場合、断面が楕円になることを証明せよ》
あなたなら、どう考えますか?
僕「しかし……なかなか難しい問題じゃないかなあ、これ」
ユーリ「お兄ちゃんならできるよ!」
僕「まずは少し図を描いてみようか。 断面が円になったり、楕円になったり、直線になったりするのは、 全部、ナイフとなる平面の角度が変わったからだよね」
ユーリ「うん。角度が変われば形も変わるね」
角度を変えれば形も変わる
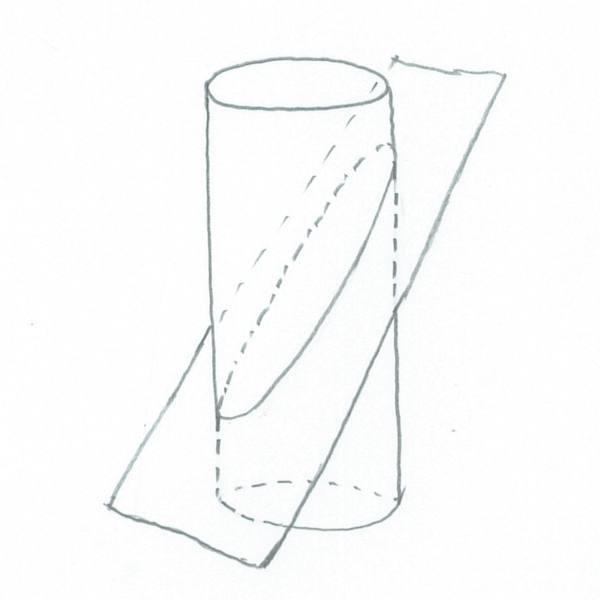
僕「だとすると、きっとこんなふうに角度を $\alpha$ としておくといいかもしれない。一回の切断で $\alpha$ は定数。決まった角度でスパッと切るから。角度を変えて切るというのは、 $\alpha$ の値を変えることに相当する」
角度を $\alpha$ とし、座標を定める

ユーリ「ふむふむ。この $x$ と $y$ は?」
僕「うん、切断に使う平面の上に《座標》を決めておこうと思ったんだ。 さっきから《断面の形》と言ってるけど、その形っていうのは、 この平面上に描かれた形のことだからね」
ユーリ「ふーん」
僕「この図の $O$ は、この円筒の中心軸と平面との交点のこと。 ここを座標の原点に取ることにすると、きっといいと思う」
ユーリ「何で?」
僕「なんとなく」
ユーリ「なにそれいいかげん!」
僕「いや、ごめん。なんとなくじゃない。僕たちのゴールを考えると、 ここに原点を置くのがいいとはっきりしている」
ユーリ「ゴール?」
僕「がく。この断面が《楕円である》と証明するのがゴールだろ?」
ユーリ「そーだけど……」
僕「じゃ、ユーリにクイズだよ。 僕たちはいまこの断面が《楕円である》といいたいわけだよね?」
ユーリ「うん、そーだね」
僕「では、何がいえたら《楕円である》といえると思う?」
ユーリ「何がいえたら……って、楕円であるといえたら。じゃないの?」
僕「それじゃ話がぐるぐるまわってしまう。 ユーリはもう楕円についていろんなことを知っている。 いまここに $x$ と $y$ の座標がある。何がいえたら《楕円である》といえる?」
ユーリ「$x$ と $y$ の……」
僕「うんうん」
ユーリ「あったじゃん、ほら。 $x$ と $y$ が出てきて、イコール $1$ になるの。 $x$ と $y$ の式」
僕「そうそう。それのこと。楕円の方程式」
ユーリ「それだ!(第83回参照)」
楕円の方程式
$$ \left(\dfrac{x}{a}\right)^2 + \left(\dfrac{y}{b}\right)^2 = 1 $$
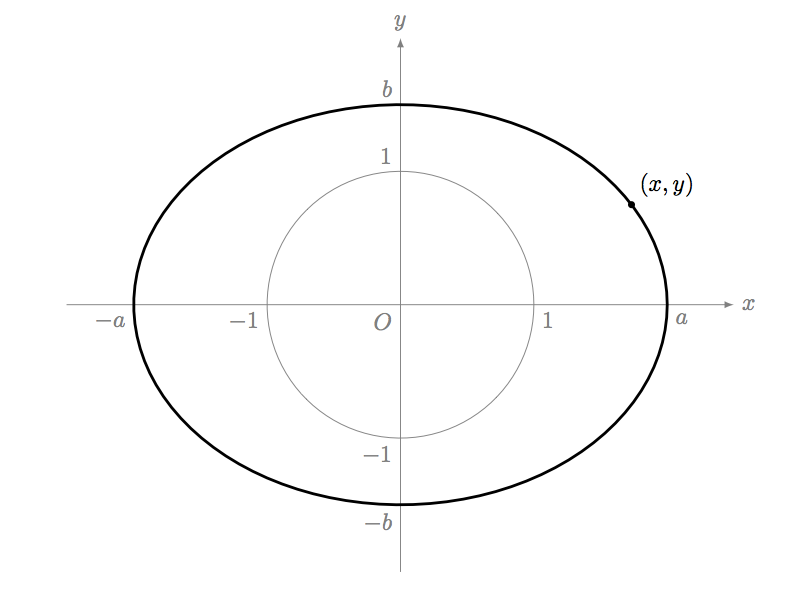
僕「そう。僕たちは楕円の方程式を知っている。 $x$ と $y$ の座標があって、点 $(x,y)$ が楕円の方程式を満たしているなら、 その点は楕円上にあるわけだ。 だから僕たちが進む道はこれで決まった。何とかして、 切断面の形が楕円の方程式を満たしていることをいえばいい」
ユーリ「ふむふむ……でも、どーやって?」
僕「それを、これから考える」
ユーリ「あ、そーなの……」
僕は少し考える。 こうすれば……わかるかな?
僕「ちょっと図を描いてみるよ、ユーリ」
ユーリ「どーゆー図?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年8月22日)