![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
僕とユーリは楕円についておしゃべりをしていた。
僕「そういえば、楕円にはおもしろい性質があるんだよ。《ないしょ話を届ける》という性質」
ユーリ「何それおもしろそう!」
僕「広い聖堂を想像する。端から端まで何十メートルもあるから、隅の方で《ないしょ話》をしても反対側には聞こえない……」
ユーリ「ふんふん」
僕「……聞こえないように思える。ところが、この聖堂は壁面がちょうど楕円の形になっていた」
ユーリ「ほー!」
僕「ほら、楕円には焦点が二つあるよね。《ないしょ話》をしたい二人が焦点のところに立つんだよ。 たとえばお兄ちゃんが片方の焦点に、そしてユーリが別の焦点に」
ユーリ「え……でも、離れてるよね?」
僕「うん、小さな声だとその距離では直接届かない。でも、焦点から焦点には《ないしょ話》のような小さな声でも届くんだよ」
ユーリ「なんで?」
僕「音が反射するからなんだ。一つの焦点から《ないしょ話》の音が出ると、まわり中に音は広がっていく。 広いから、相手に直接届く音はほんの一部。でも、まわりに広がった音はやがて楕円形の壁に当たって反射する。 反射した音はどこに向かうかというと、すべてもう一つの焦点に向かう」
ユーリ「へー!」
僕「焦点からいったん広がった音が、壁で反射してもう一つの焦点に集まる。 楕円形にはそんな性質があるんだ」
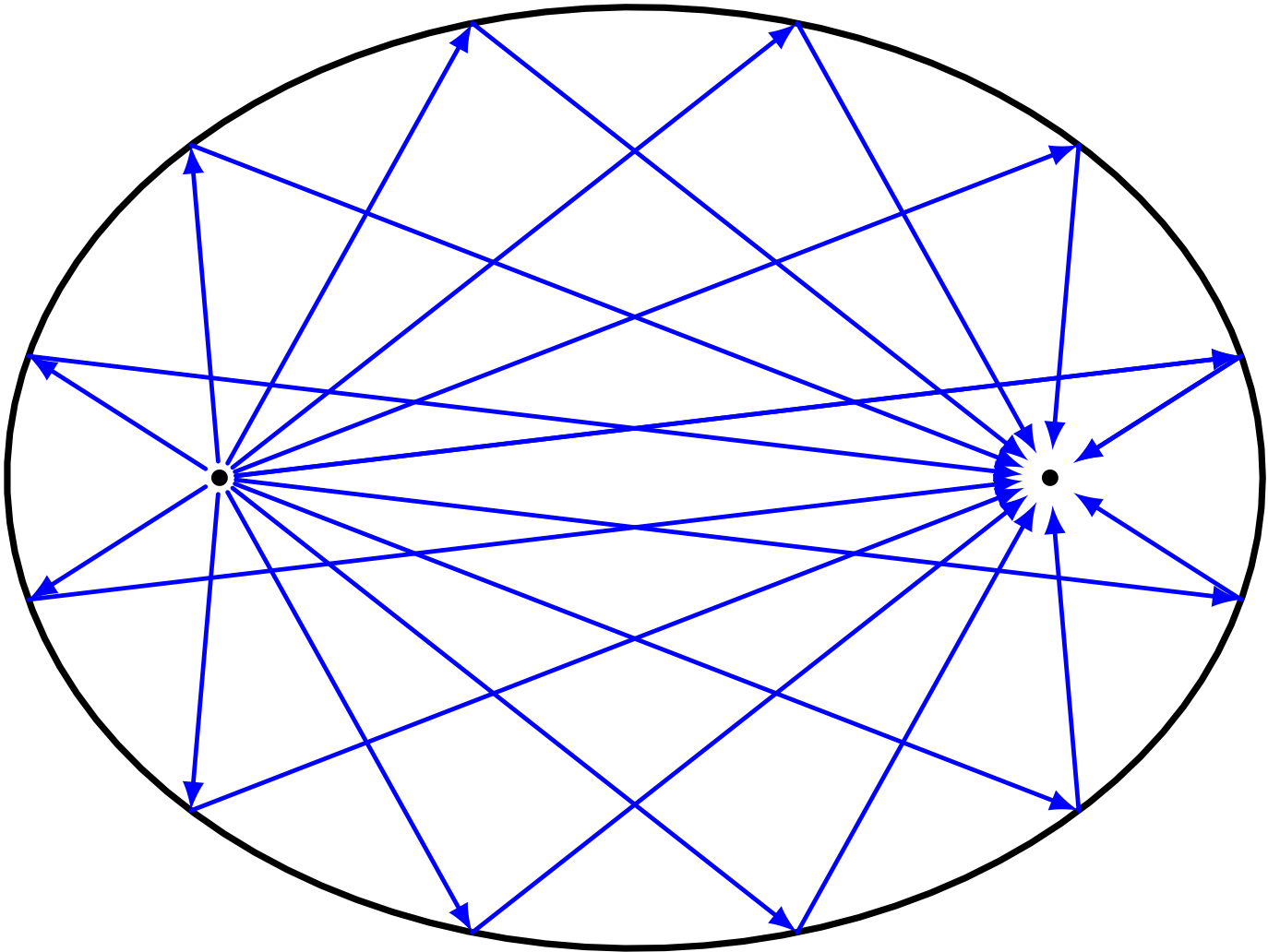
楕円は焦点から焦点に《ないしょ話》を伝える
ユーリ「ねーそれほんとの話?」
僕「ほんとうの話だよ。《ささやきの回廊》と呼ばれる現象で、そういう建築物が世界中のあちこちにあるそうだよ」
ユーリ「おもしろいにゃあ……あれ? でも変なの」
僕「何が?」
ユーリ「楕円の焦点って、糸を引っ掛けたときのピンの位置だよね?」
僕「そうだよ。楕円を描くときに使ったピンの位置」
楕円の描き方
1. ピンを二本立てる。
2. 糸を輪にしてピンに掛ける。
3. 糸がたるまないようにしながら、シャープペンでぐるっと一回りする。
4. 楕円のできあがり。
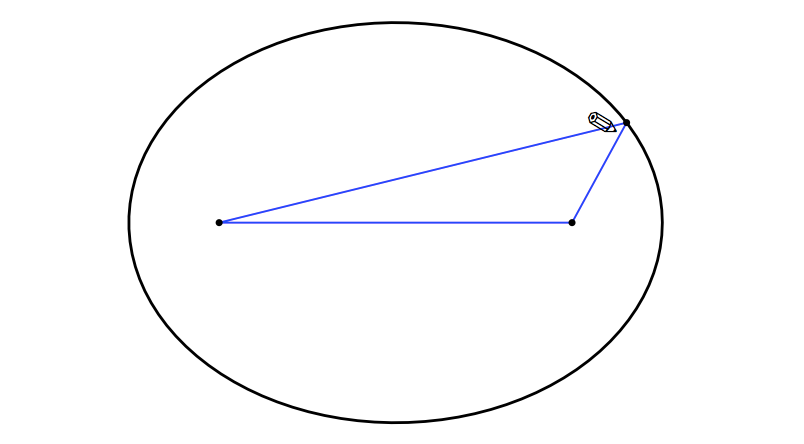
ユーリ「これって、反射とは何も関係ないじゃん?」
僕「まあ、そうだね。《焦点からの距離の和が一定である》という性質と、 《ないしょ話を反射で伝える》という性質は関係ないねえ……少なくとも直接は関係ない。 でも、この楕円の形はそういう性質を持っているってことだね」
ユーリ「えーと、ひっかかるにゃ。何でそんな性質を持つの?」
僕「《何で》と言われても困るけど……」
ユーリ「だって、すごく不思議じゃん? 楕円の壁のどこに当たっても、 きっちり相手の焦点に伝わるんでしょ?」
僕「もともと《焦点》という名前はそこから来てるんだと思うけどな。 つまり、楕円の壁が鏡になっているとして、焦点の片方から放った光は反対側の焦点を通る」
ユーリ「そして、戻ってくる?」
僕「戻ってくる? ああ、そうなるね。焦点の片方から放った光は反対側の焦点を通って、 また壁で反射して自分に戻ってくるね。光が戻ってくる向きは放ったときの向きとは違うけど」
ユーリ「うっわー、不思議! お兄ちゃん、証明してよ!」
僕「証明?」
ユーリ「うん! だって、ほんとうに楕円にそういう性質があるなら、 証明できるはずでしょ?」
僕「まあ……そうか。そういえば、証明しようと思ったことないなあ。 どこかの本で《ささやきの回廊》の話を読んで、図を見てなるほどと思ったけど」
ユーリ「証明して!」
問題1(ないしょ話を伝える楕円)
楕円の二つの焦点を $A, B$ とする。 $A$ から出た光線は、楕円で反射すると $B$ を通ることを証明せよ。

僕はちょっと考える。楕円の方程式は知っているし、 それから任意の点での接線の方程式も知っている。 あとは法線ベクトルを考えて、光線の入射角と反射角が等しいことをいえばいいだろう。 角度の等しさをいうにはベクトルの内積を考えることになるのかな。
僕「うーん……でも」
ユーリ「どう? できそう?」
僕はさらに考える。 でも、それをユーリに説明する自信はないな。 接線の方程式、法線ベクトル、ベクトルの内積……それらをぜんぶ天下りに出してみせて証明といってもなあ……
僕「よし、図形として考えてみるか」
ユーリ「へ? 図形として考えるって、あたりまえじゃないの?」
僕「方程式を出さずに考えてみるってこと。うまくいくかどうか自信ないけどね……まず、図を描いてみる。 楕円と、焦点と、反射点。焦点は $A, B$ で、反射点は $P$ としよう」
焦点 $A, B$ と反射点 $P$
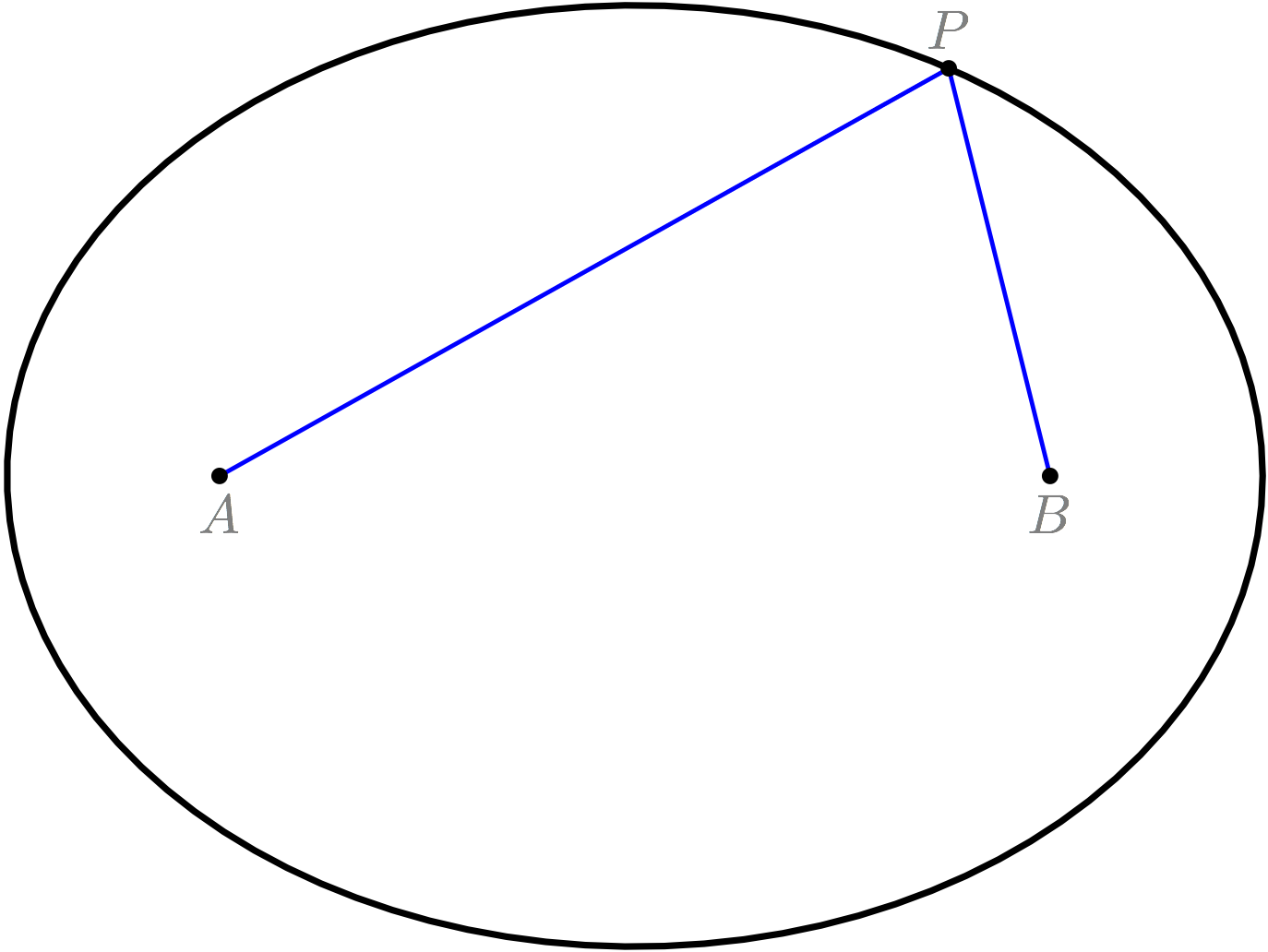
ユーリ「わくわく!」
僕「この問題のポイントは《反射》ということをどうやって数学的に表現するかだね。 それから、反射した光線が《焦点を通過する》ということも」
ユーリ「うんうん!」
僕「楕円の壁が鏡になっていて、 $P$ で反射するというのは、 平らな鏡を持ってきて、楕円の点 $P$ で接するように置いたときに、 《$AP$ と接線の角度》と《$BP$ と接線の角度》が等しくなるということ。 だから、その二つの角度が等しくなることを示すのが目標」
反射した光が焦点を通る

ユーリ「なーるほど! そんでそんで?」
僕「うん、だいぶわかってきたぞ……僕たちが使える条件は、この図形は《楕円である》ということ。 つまり《二つの焦点からの距離の和が一定》だよね。これが楕円の条件。 さっきはこの距離の和のことを $2R$ と置いた(第83回参照)」
ユーリ「あ、そっか。楕円の描き方がそのまま条件なんだ」
僕「それで、鏡を作り出すんだから……うん、こういう点 $C$ を作ってみよう。 焦点 $A$ から反射点 $P$ を通って、反射せずにまっすぐ延長して、ちょうど $AC$ の長さが $2R$ になるような点として、 $C$ を描く。つまり、 $PC = PB$ になるようにするということだね。」
新たな点 $C$ を描く
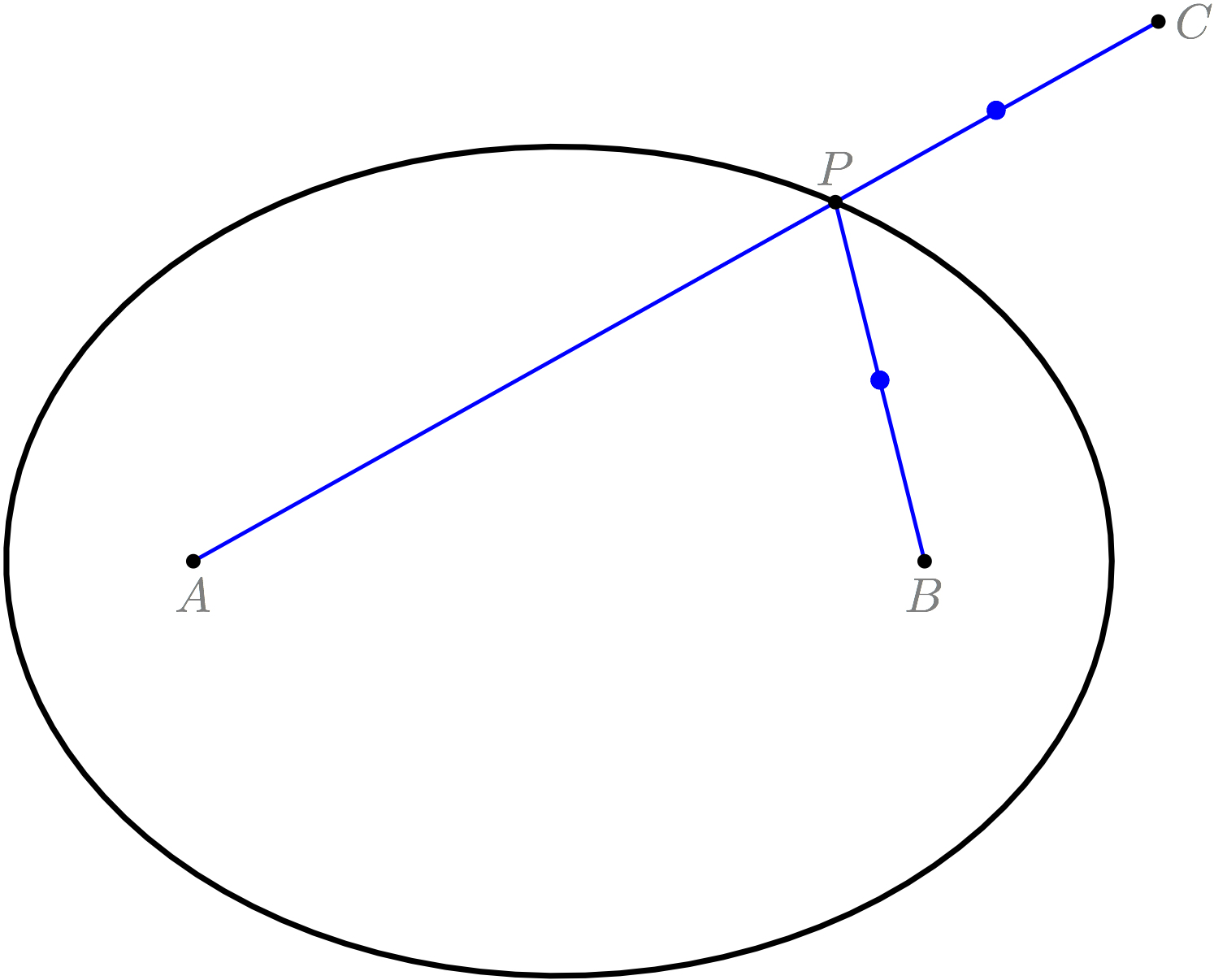
線分 $AP$ を延長して、 $PC = PB$ になる点を $C$ とする。 このとき $AC = 2R$ となる($2R = AP + PB$)。
ユーリ「あ! この点 $C$ って《鏡に映った $B$》じゃない?」
僕「ユーリは賢いなあ。きっとそうなるんだけど、まだそうじゃない」
ユーリ「どゆこと?」
僕「点 $C$ は、点 $B$ を鏡に映して作ったわけじゃない。 $AP$ を延長して $AC = 2R$ になるように点 $C$ を取っただけ」
ユーリ「ふむふむ?」
僕「これから、点 $B$ と点 $C$ を使って鏡を作るんだよ。うまく鏡が作れたら証明は終わり」
ユーリ「鏡を作るって?」
僕「さっきもいったように、反射点 $P$ で楕円に接する接線を作るということ。 まあちょっと見てて。線分 $BC$ の中点として点 $D$ を取る」
線分 $BC$ の中点として点 $D$ を取る

線分 $BC$ の中点として点 $D$ を定める。
ユーリ「……」
僕「そして、二点 $D$ と $P$ を通る直線 $\ell$(エル)を描く。これが鏡となる接線だね」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年7月25日)