第88回 シーズン9 エピソード8

切断エリプス（後編）

ユーリ「ソーセージの断面は、楕円！　証明できた！」

僕「けっこうたいへんだったなあ（第87回参照）」

ユーリ「いやいや、なかなかでしたよ、お兄ちゃん」

僕「図に描くのはやっぱり大事だ」

ユーリ「お兄ちゃんって、よくサイン・コサイン・タンジェント教えてくれるじゃん？　あれってほんとに使うんだね」

僕「《ほんとに使う》って、何のこと？」

ユーリ「いやほら、サイン・コサイン・タンジェントって、三角形描いて、いろいろ計算するじゃん。 でも、さっきは《円筒を平面で切った形が楕円になる》ことを証明するときに、 $\sin \alpha$ が出てきた」

僕「そうだね」

ユーリ「そーゆーこと！」

僕「三角関数の $\cos$ や $\sin$ や $\tan$ は、とてもよく使う数学の道具だよ、ユーリ。 テトラちゃんなら《バトルの武器ですっ！》なんて言いそう」

ユーリ「テトラさん？」

僕「三角関数っていかにも難しそうに見えるけれど、 角度が登場するときにはしょっちゅう使う道具だよ。 それからもちろん、円や楕円もそうだね」

ユーリ「うん。お兄ちゃんがサイン・コサインの話するとき、 必ず円を描くよね」

僕「そう。こういう円だろ？　原点を中心にして、 半径が $1$ の単位円」

ユーリ「そーそー！」

僕「単位円の上にある点を $(x,y)$ とすると、 $x = \cos \theta$ で、 $y = \sin \theta$ で表せる。 角度 $\theta$ を動かしていったとき、 $(x,y)$ は変化していくけれど、 そのときの $x$ と $y$ の値として、 $\cos \theta$ と $\sin \theta$ が定義されるんだよ。 タンジェントは $\tan\theta = \dfrac{\sin \theta}{\cos \theta}$ で定義するね。 円を扱うときには自然に三角関数が出てくる」

ユーリ「三角なのに必ず円が出てくるっておかしーね」

僕「そうだね。直角三角形の代表的な定理は《三平方の定理》（ピタゴラスの定理）だけど、それを使うと、 $\cos \theta$ と $\sin \theta$ のあいだにどんな関係があるかもわかるよ。コサインとサインの関係式」

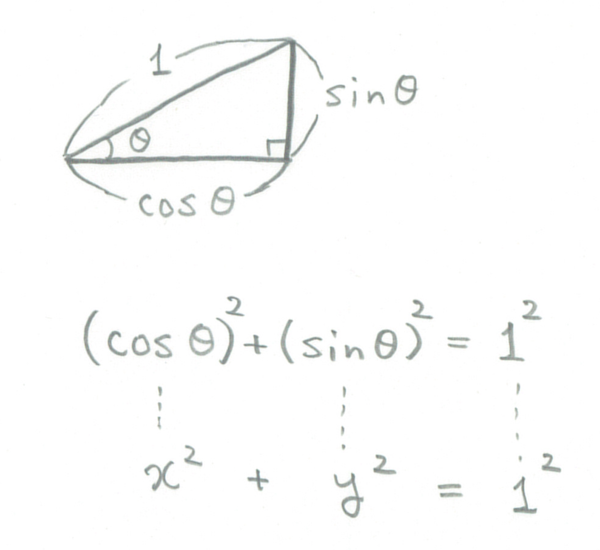
ユーリ「ふんふん」

僕「$\cos^2 \theta + \sin^2 \theta = 1$ というのは、 三角関数でいちばん基本的な式なんだけど、 それは原点中心で半径が $1$ の円の方程式 $x^2 + y^2 = 1$ だといってもいいんだよ」

ユーリ「円の方程式、ね」

僕「そうそう。そして、この円を横方向に $a$ 倍して、 縦方向に $b$ 倍したものが楕円になる。 逆にいえば、楕円を横方向に $a$ 分の $1$ して、 縦方向に $b$ 分の $1$ したら単位円になるということ」

ユーリ「うん、こないだやったやった（第83回参照）」

僕「円筒を真横（$90$ 度）じゃなくて、角度 $\alpha$ の平面で切ったとき、 $a = \dfrac{1}{\sin \alpha}, b = 1$ という値になった（第87回参照）」

ユーリ「うんうん」

球を入れる

ユーリ「こないだの《ささやきの回廊》もそーだし、 円筒を平面で切るのもそうだけど、楕円っておもしろいね」

僕「そうだね」

ユーリ「それに、お兄ちゃんが何でもちゃちゃっと証明してくれるのがすごいよ！」

僕「何でもじゃないよ。証明できるものだけ」

ユーリ「アニメネタ禁止」

僕「てへ」

ユーリ「そんなことより、楕円でもっとおもしろい話ないの？　ねーねー！」

僕「そうだなあ……たとえば、円筒の中に《球を入れる》という話がある」

ユーリ「球を入れる？」

僕「そう。円筒にぴったり入る大きさのボールみたいなものを考えればいいよ。 円筒の半径と球の半径が等しいということ。 円筒を斜めに切った平面を固い紙だとすると、 円筒に入れたボールはすうっと降りていって、平面にそっとタッチして止まる」

ユーリ「ふんふん？」

僕「平面と球は一点で接する……図に描いてみようか」

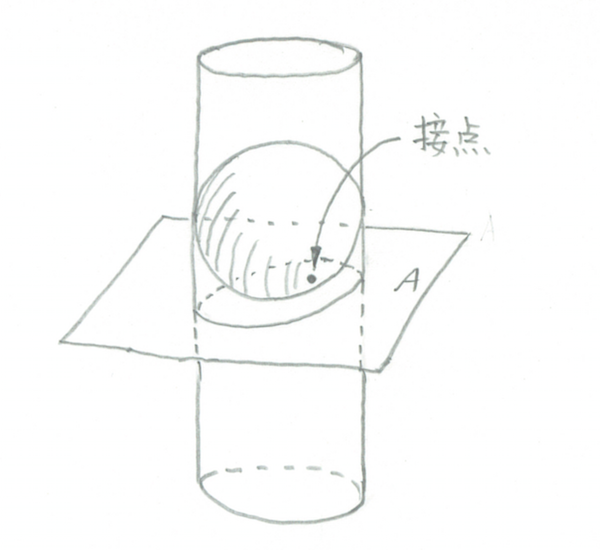
ユーリ「ほほー、なるほど。この $A$ が平面で、斜めに切ってるんだね」

僕「そうそう。そこに球を入れた。そうすると一点で接する。 もしも平面 $A$ が水平になっていたら、この《接点》は断面の円の中心になる」

ユーリ「……でも、平面 $A$ が水平じゃなかったら？」

僕「水平じゃなかったら……この接点は何だと思う？」

ユーリ「何か特別な点なの？」

僕「そうだよ。楕円にとって特別な点。ユーリも知ってるはず」

ユーリ「えっ！　《楕円の焦点》なの？　もしかして！」

僕「大正解！　そうなんだよ」

ユーリ「う、うわーっ！　なにそれすごい！」

僕「不思議だよね。円筒を斜めに平面で切る。円筒に球を入れる。 球と平面の接点は、断面となる楕円の焦点に一致する。 これはとってもきれいな性質だよね！」

ユーリ「へーっ！　……あれ、でも何か変だよ」

僕「何が？」

ユーリ「だってさ、焦点っていうのは、楕円を描くときに使ったよね。 ピンを刺したところでしょ？（第83回参照）」

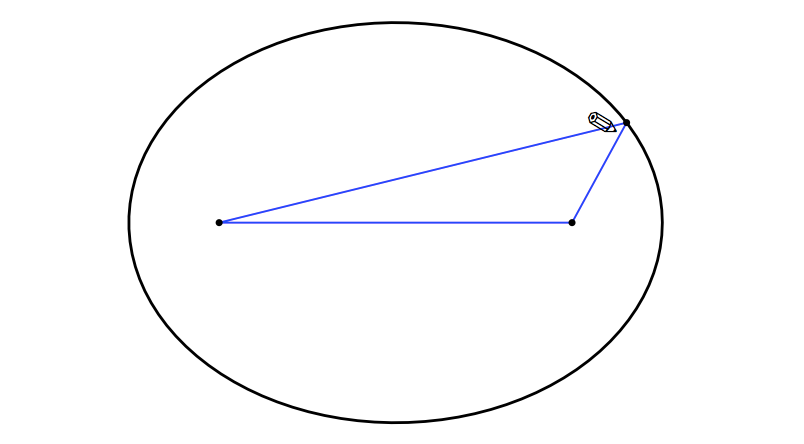
僕「そうだね」

ユーリ「なんで、その焦点が、入れた球と関係があるの？　ぜんぜん関係ないじゃん！」

僕「うーん、まあ確かに関係はないといえばないんだけど」

ユーリ「偶然？」

僕「いや、どんな角度で切った場合でも、必ず楕円の焦点で接するから、 偶然というわけじゃない。まあ、だから楕円の性質としかいいようがないけど」

ユーリ「もやもやするにゃ……あっ！　お兄ちゃん！　これも証明してよ！」

僕「え……」

ユーリ「そーだよ！　お兄ちゃんならできるよ！」

僕「これは……どうすればいいのかな……」