第447回 シーズン45 エピソード7

サービト・イブン・クッラ（前編）

代数的計算の幾何的正当化

僕「……だから、アル＝フワーリズミーのこの方法を二次方程式 $$ x^2 + bx = c \qquad (b > 0, c > 0) $$ に当てはめるなら『$b/2$ を二乗して $c$ を加えて正の平方根をとって $b/2$ を引く』ということだから、 $$ x = \SQRT{\left(\frac{b}2\right)^2 + c} - \frac{b}{2} $$ という正の解を得る解法になる——ということだね」

ユーリ「その調子で $6$ 通りのパターン（第446回参照）ぜんぶ書いてくのは、 めんどいにゃあ（・・・）」

テトラ「ユーリちゃんのいう通りですよね。 正の数に限定することで考えやすくところもありますけど、 場合分けが多くなってしまうのは大変ですね」

僕「こっちのパネルには図形が描いてあるね」

ユーリ「あっ、めんどくさい！　次のパネル行こ！」

僕「そんなに先を急いでもつまらないよ。この説明は $x^2 + 10x = 39$ の解法を図形的に説明しようとしてるんだね」

ユーリ「こーゆーの、動画にしないとわかんないよ」

僕「9世紀の時代には動画はないよ」

テトラ「その時代でも、図形を使って説明するというのは納得感を生んだんでしょうね」

ユーリ「たった一つしか図形なくても？」

僕「自分の頭の中で動画にするわけだね」

テトラ「これって……当時の人には《最先端の数学》だったわけですよね。 それを、あたしたちが追うことができるってすごいと思います」

ユーリ「あっ、なーんだ！　これだけの話？」

僕「早いな」

ユーリ「こんなのカンタンじゃん！」

テトラ「それじゃ、ユーリちゃん。 $x^2 + 10x = 39$ の解法を図形で教えてくださいな」

ユーリ「面積 $x^2$ を持つ正方形 $AB$ って、ココのことでしょ？

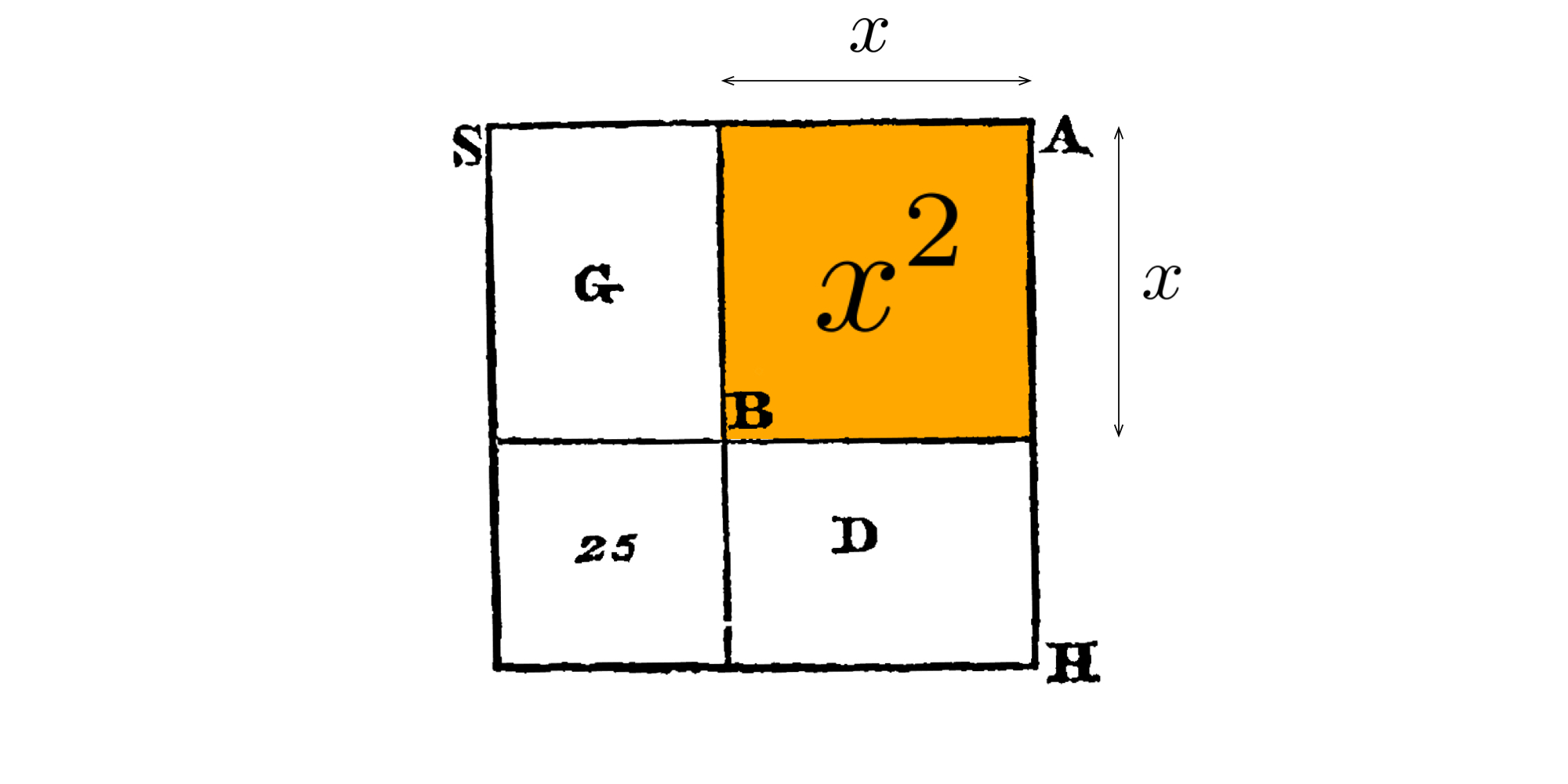
正方形なんだから、一辺が $x$ で、その $x$ を求めればいい」

僕「そうだね」

ユーリ「二つの長方形 $G$ と $D$ ってココのこと。 $x^2 + 10x = 39$ の $10x$ を二つに分けて、面積は $5x$ ずつ。 一辺を正方形の $x$ に合わせると別の辺は $5$ になる。

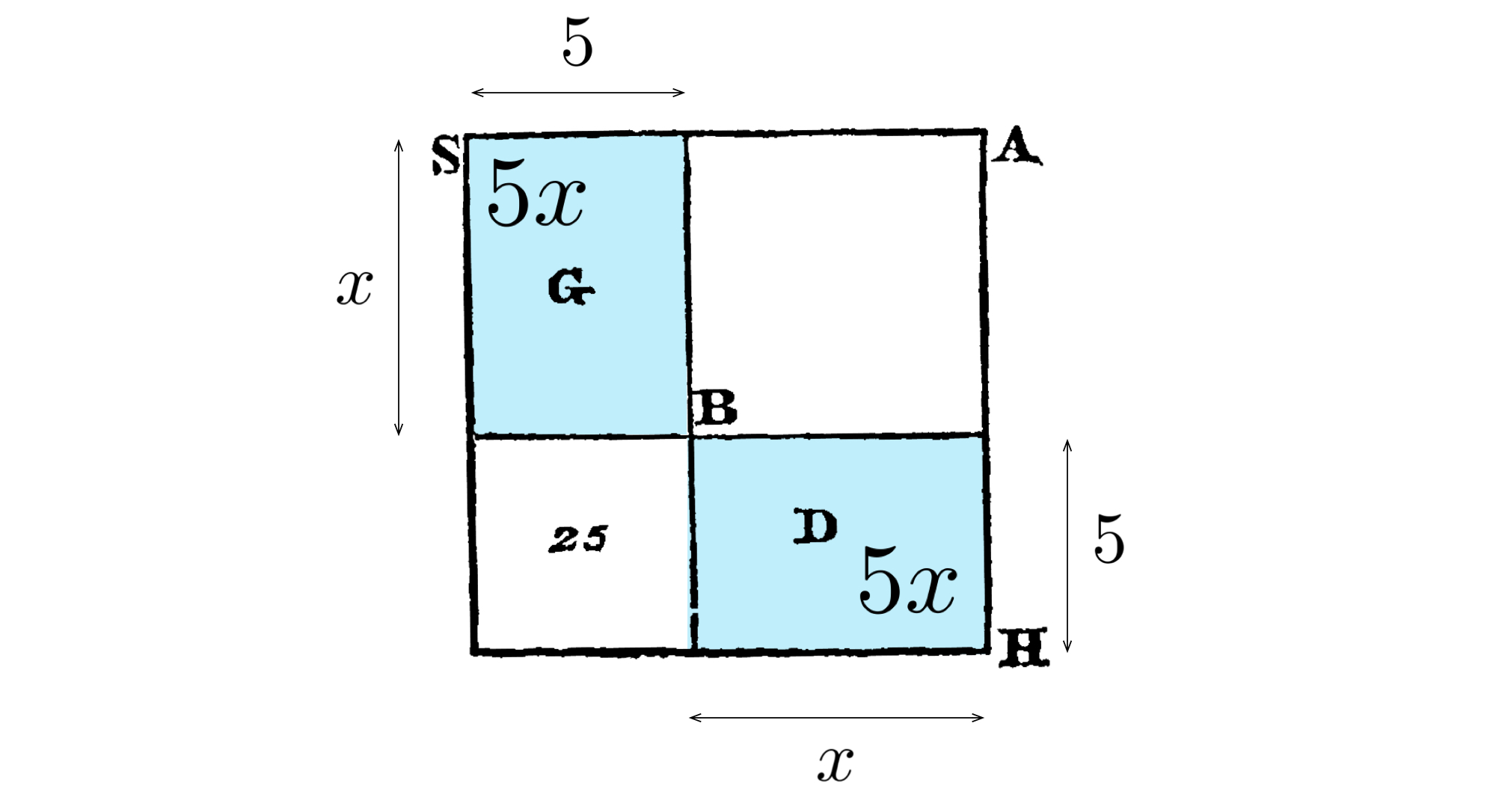
正方形 $x^2$ と長方形 $5x$ を二つ足すと面積は $x^2 + 10x$ になる。

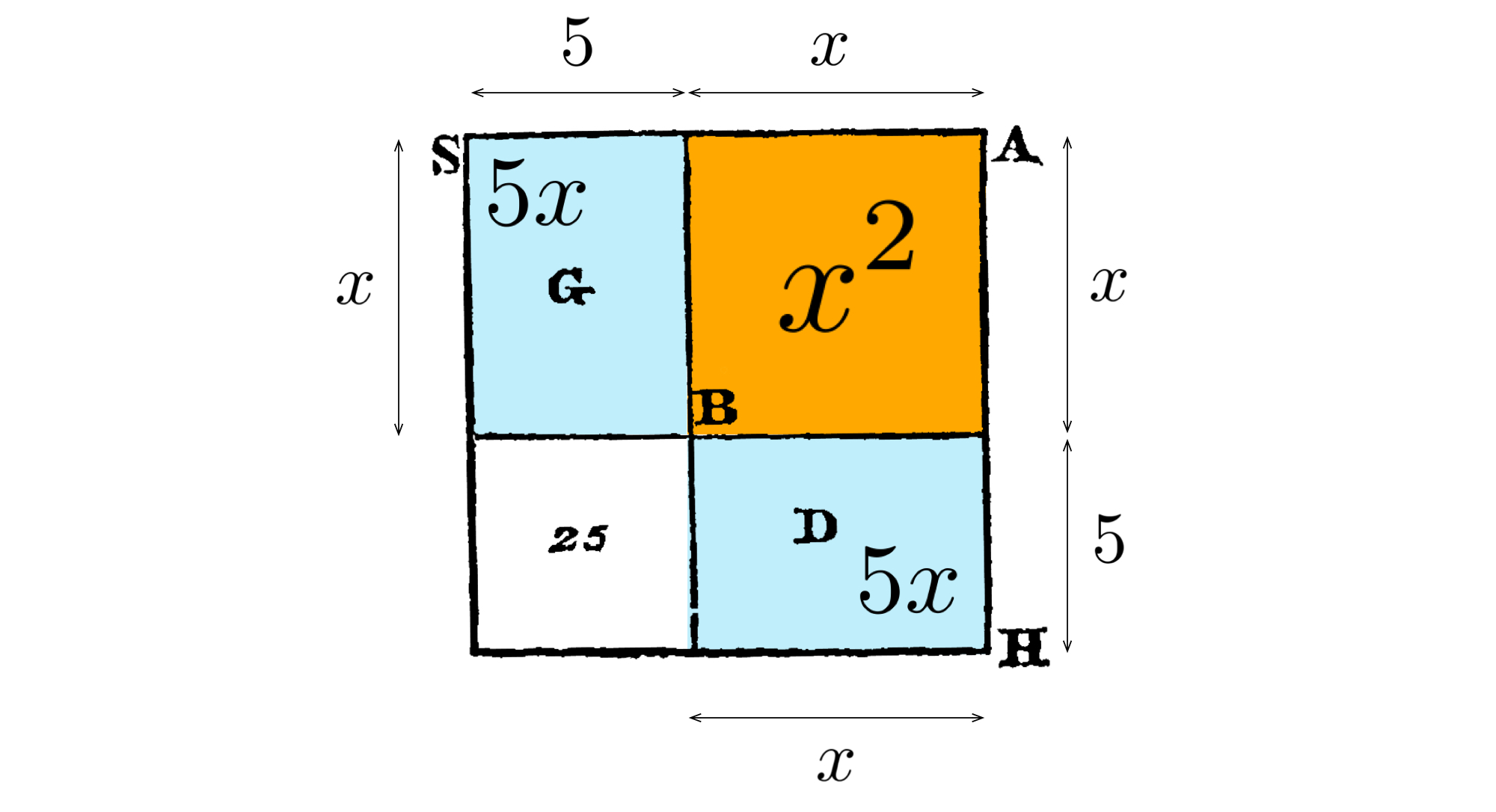
二つの長方形 $G$ と $D$ の、 $5$ の辺二つで作ったちっちゃな正方形が 左下にできて、その面積は $5\times 5 = 25$ になる。 ココのこと。

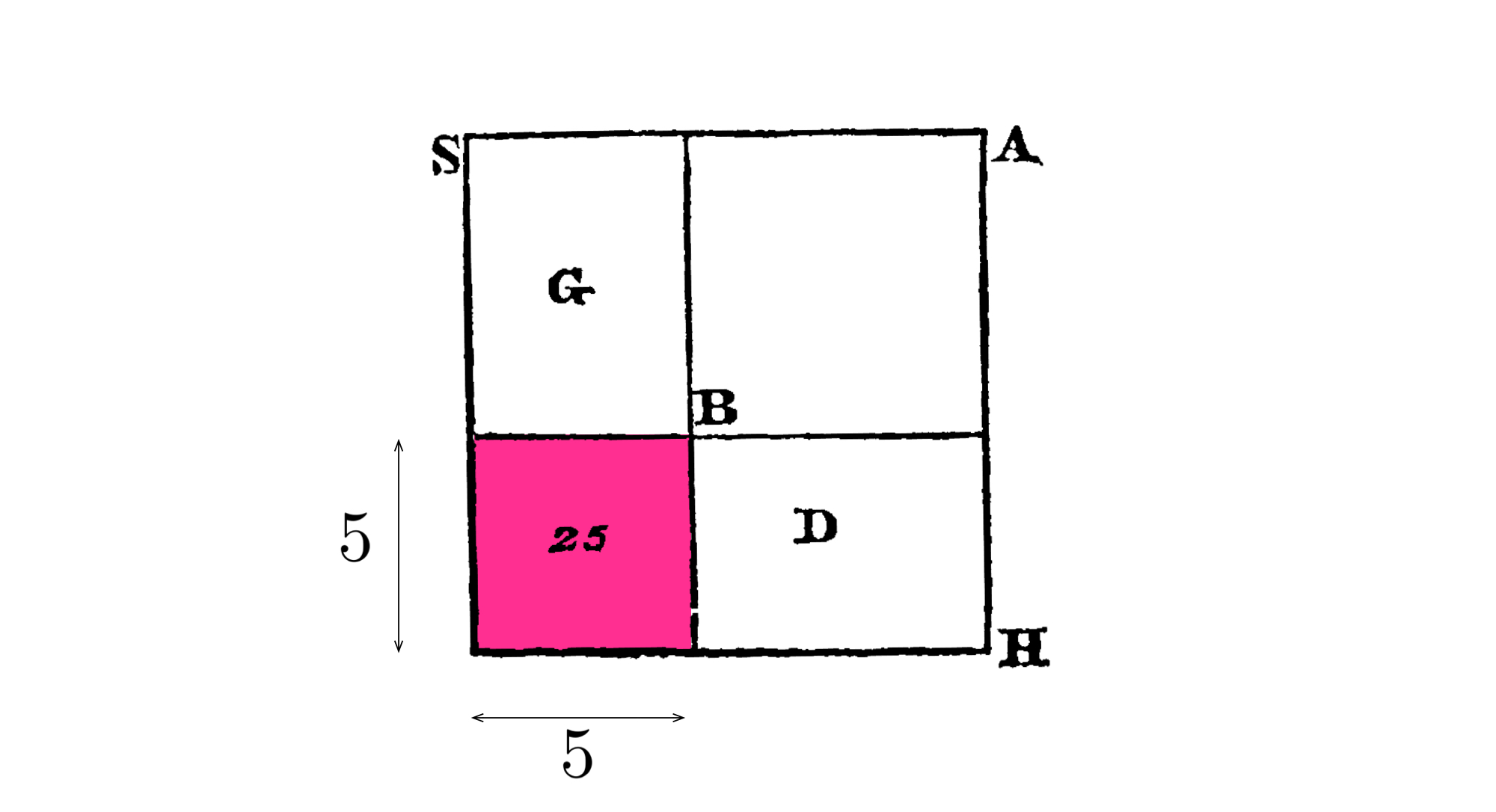
$x^2 + 10x = 39$ に $5\times 5 = 25$ を足したら、 おっきな正方形 $SH$ ができる。これは全体の正方形のこと。

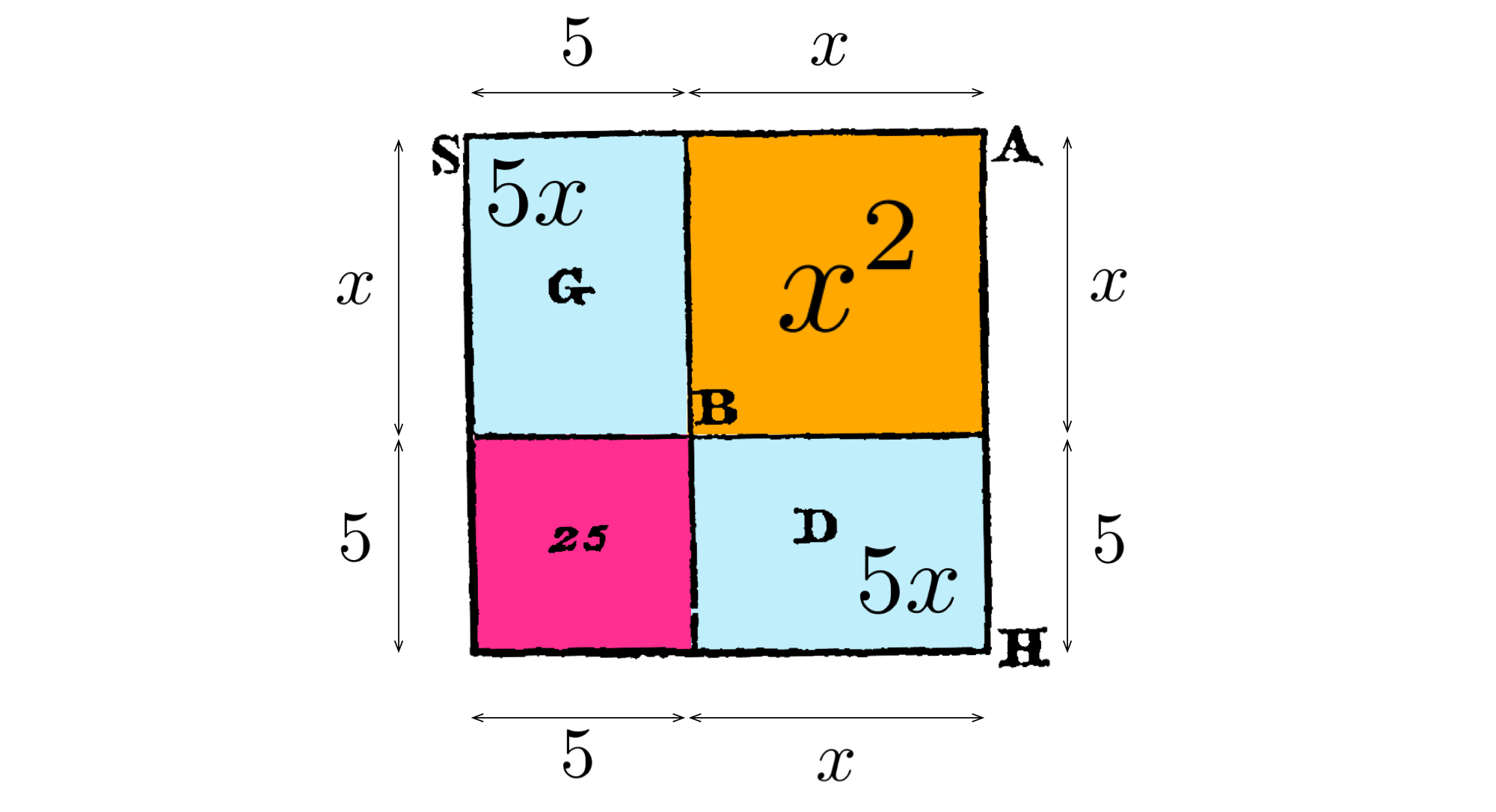
あとは $39 + 25 = 64 = 8^2$ だから、 おっきな正方形 $SH$ の一辺は $8$ になるし、 そこから $5$ を引いた $3$ が正方形 $AB$ の一辺 $x$ になる！」

僕「手早いなあ」

ユーリ「全然めんどくさくなかった」

僕「そうだよね。一見、複雑で面倒そうに見えたとしても——」

ユーリ「ストーップ！　お兄ちゃん、 いま《先生トーク》を始めようとしたね？」

僕「お？」

ユーリ「『一見、複雑でめんどーそーに見えたとしても、 きちんと取り組んでみると、意外とカンタンなんじゃ。 ゆめゆめサボることなかれ……』みたいな」

僕「キャラ崩壊してるぞ」

テトラ「ともかく、長い文章で解法の手順を示されるよりも、図があった方がわかりやすいのは確かだと思います。 もちろん、図を見て《わかったつもり》になるのはまずいですけど……」

僕「図を使ったアル＝フワーリズミーの説明は、 結局のところ、二次方程式を平方完成（へいほうかんせい）で解いているようすがよくわかるね」

テトラ「ああ、確かにそうですね！」