![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕：数学が好きな高校生。
テトラちゃん：僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ここは高校の図書室。いまは放課後。
僕は後輩のテトラちゃんといっしょに図形の問題をベクトルを使って考えていた（第436回参照）。
問題を解いた後「どうしてベクトルを使うのか」についての《数学トーク》を楽しんでいるところ（第437回参照）。
テトラ「……先輩、他にもベクトルの問題は何かご存知ですか？ もっと別の問題も解いてみたいです！ あ、あまり難しくないものでお願いします」
僕「そうだなあ……じゃあ、こんな問題はどう？」
問題2
四面体 $\TT{ABCD}$ がある。
なお、 四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ は一般の位置にある。 すなわち、この四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ は一つの平面上にはなく、 どの三点を選んでも一直線上にはない。
参考：藤田宏他『新課程 大学への数学IIB』（研文書院、1975年）
テトラ「まず問題を読ませてください。四面体 $\TT{ABCD}$ があって……」
僕「……」
テトラ「……ああ、ダメです、ダメです！ 図を描くのを忘れていました。 図を描きながら読まないと、 わけがわからなくなりますね」
僕「うん、図形問題は、 まず《図をかけ》というポリアの指示にしたがった方がいいよね。 うまく描けなかったら描き直せばいいんだし」
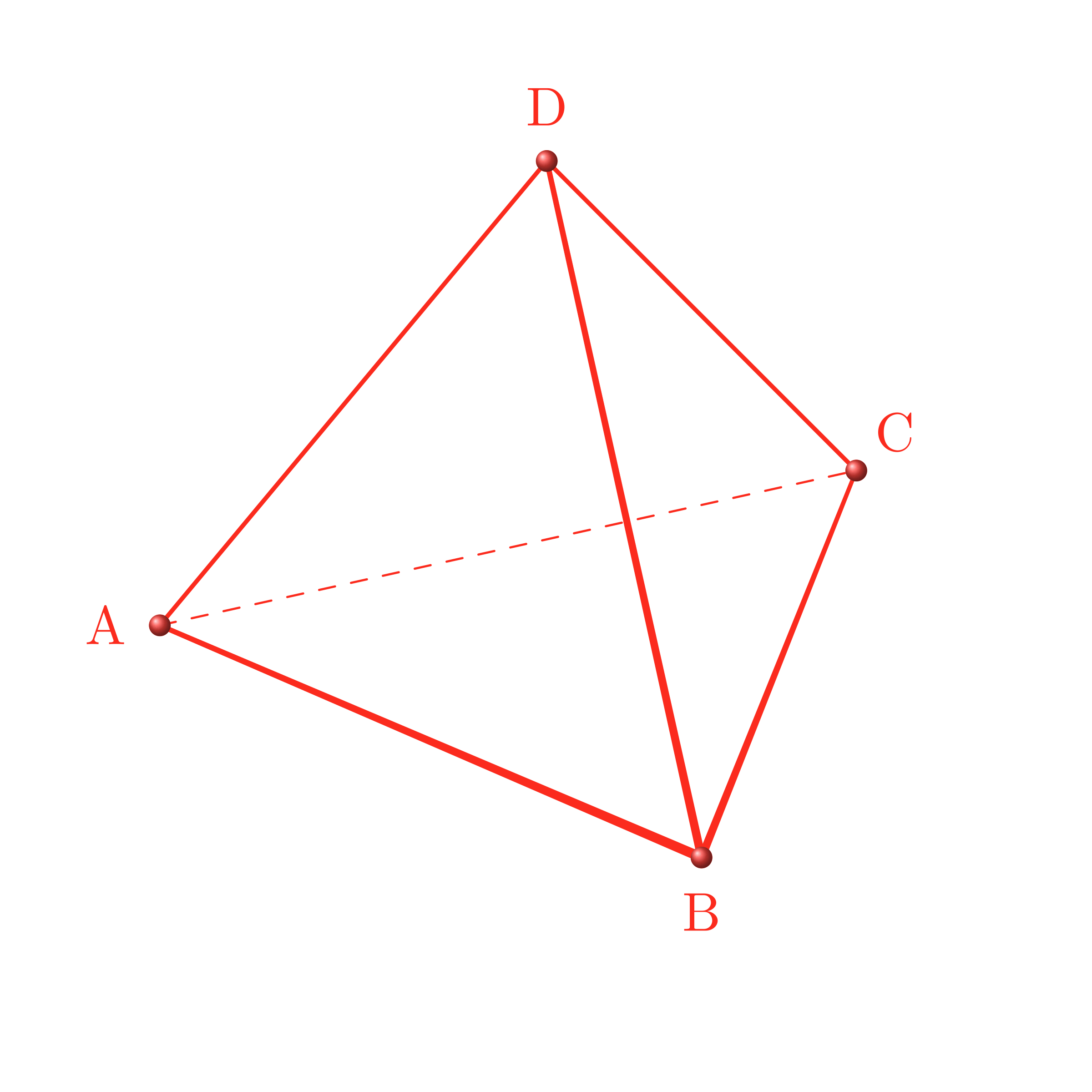
テトラ「では、図を描きながら問題を読むことにします。 四面体 $\TT{ABCD}$ がある……ということは、 こうなります」
図を描きながら問題を読む（１）：四面体 $\TT{ABCD}$ がある。
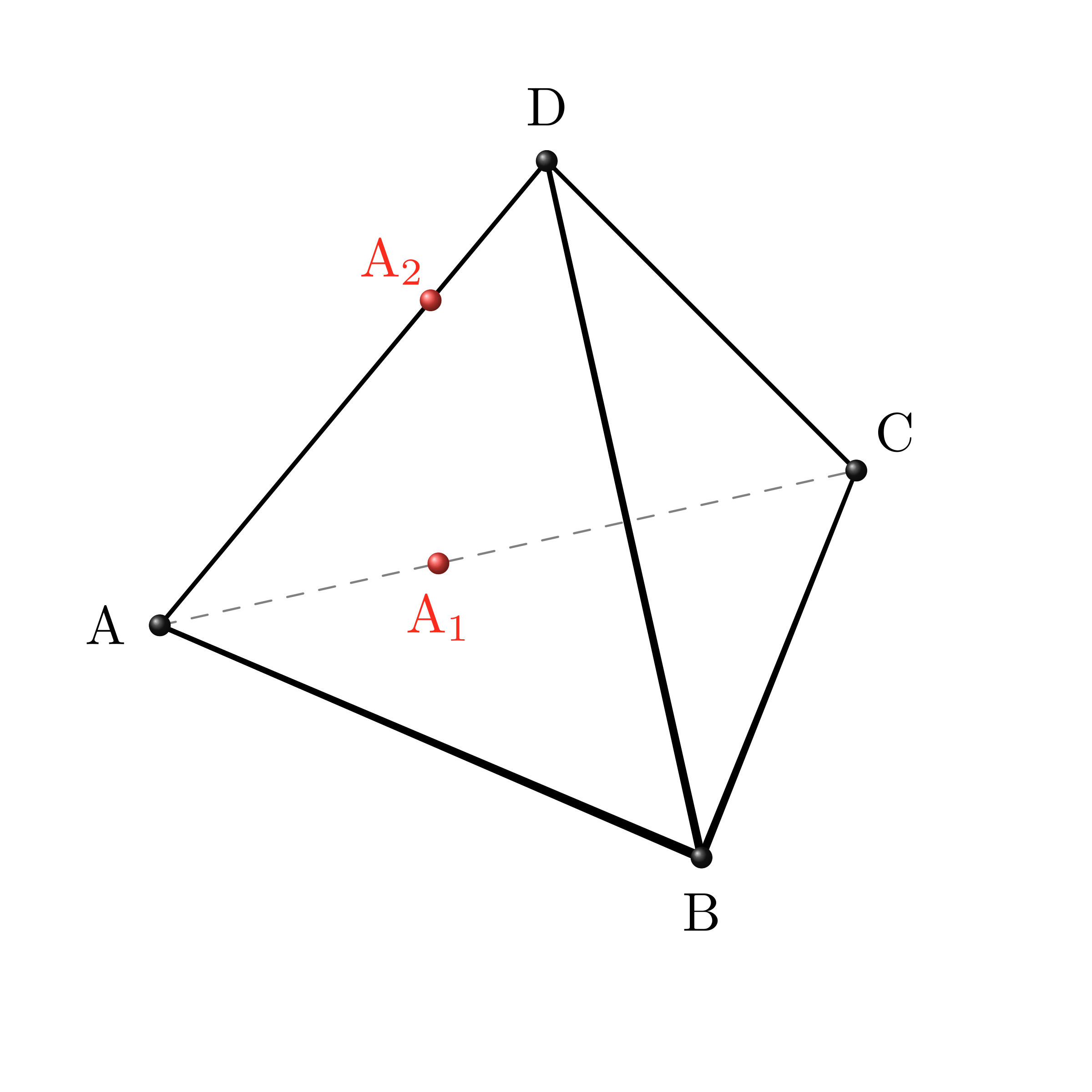
テトラ「それから、辺 $\AC,\AD$ 上にそれぞれ点 $\Ai,\Aj$ をとります。つまり、 辺 $\AC$ の上に点 $\Ai$ をとって、 辺 $\AD$ 上に点 $\Aj$ をとることになりますから……図はこうなります。
図を描きながら問題を読む（２）：辺 $\AC,\AD$ 上にそれぞれ点 $\Ai,\Aj$ をとる。
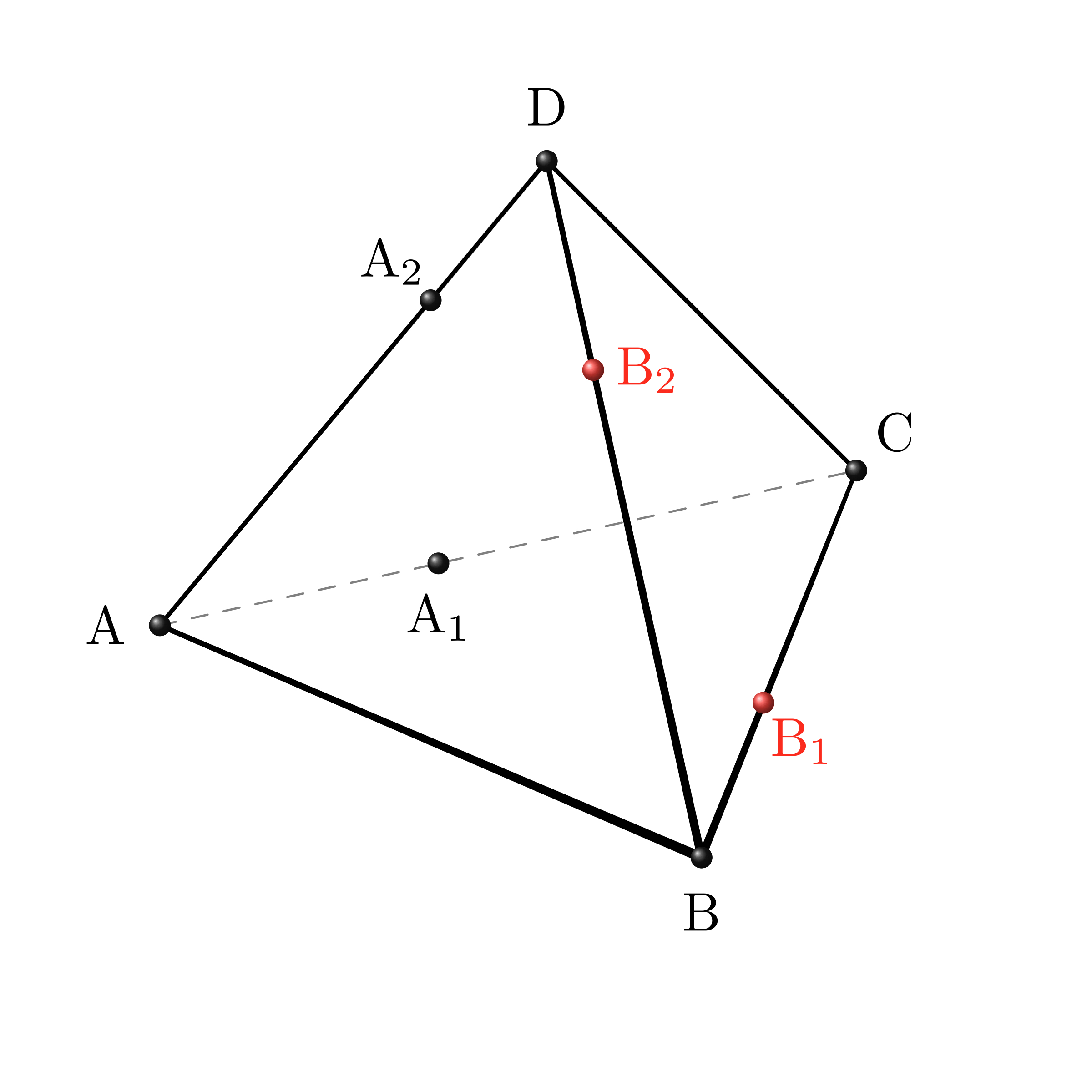
テトラ「同じように、辺 $\BC,\BD$ 上にそれぞれ点 $\Bi,\Bj$ をとります。 今度は辺 $\BC$ 上に点 $\Bi$ をとって、 辺 $\BD$ 上に点 $\Bj$ をとることになります……こうですね。 はい。だいたい様子がわかってきました」
図を描きながら問題を読む（３）：辺 $\BC,\BD$ 上にそれぞれ点 $\Bi,\Bj$ をとる。
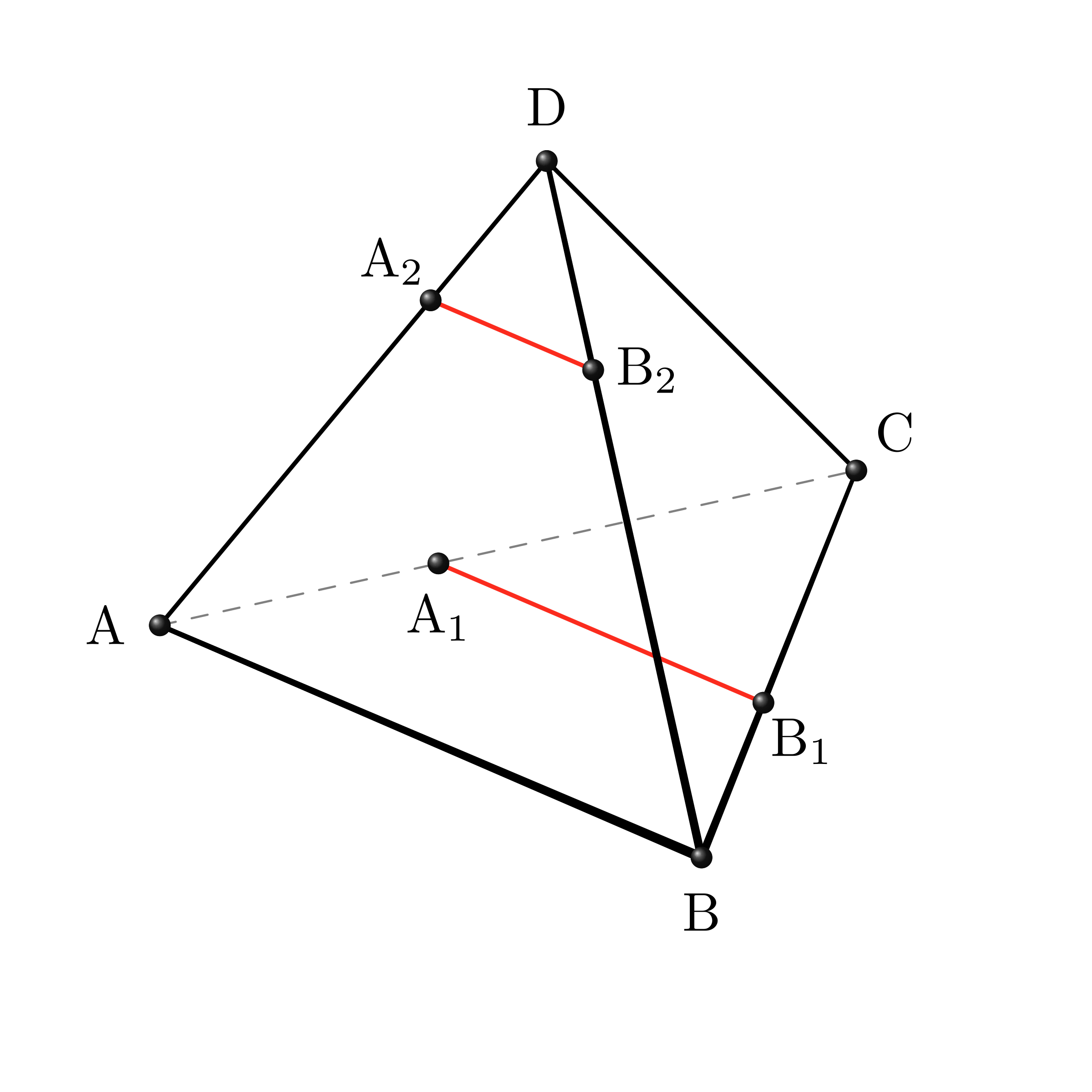
テトラ「次に、線分を二つ引くんですね。 線分 $\AiBi$ が線分 $\AjBj$ と平行ならば……」
図を描きながら問題を読む（４）：線分 $\AiBi$ が線分 $\AjBj$ と平行ならば……
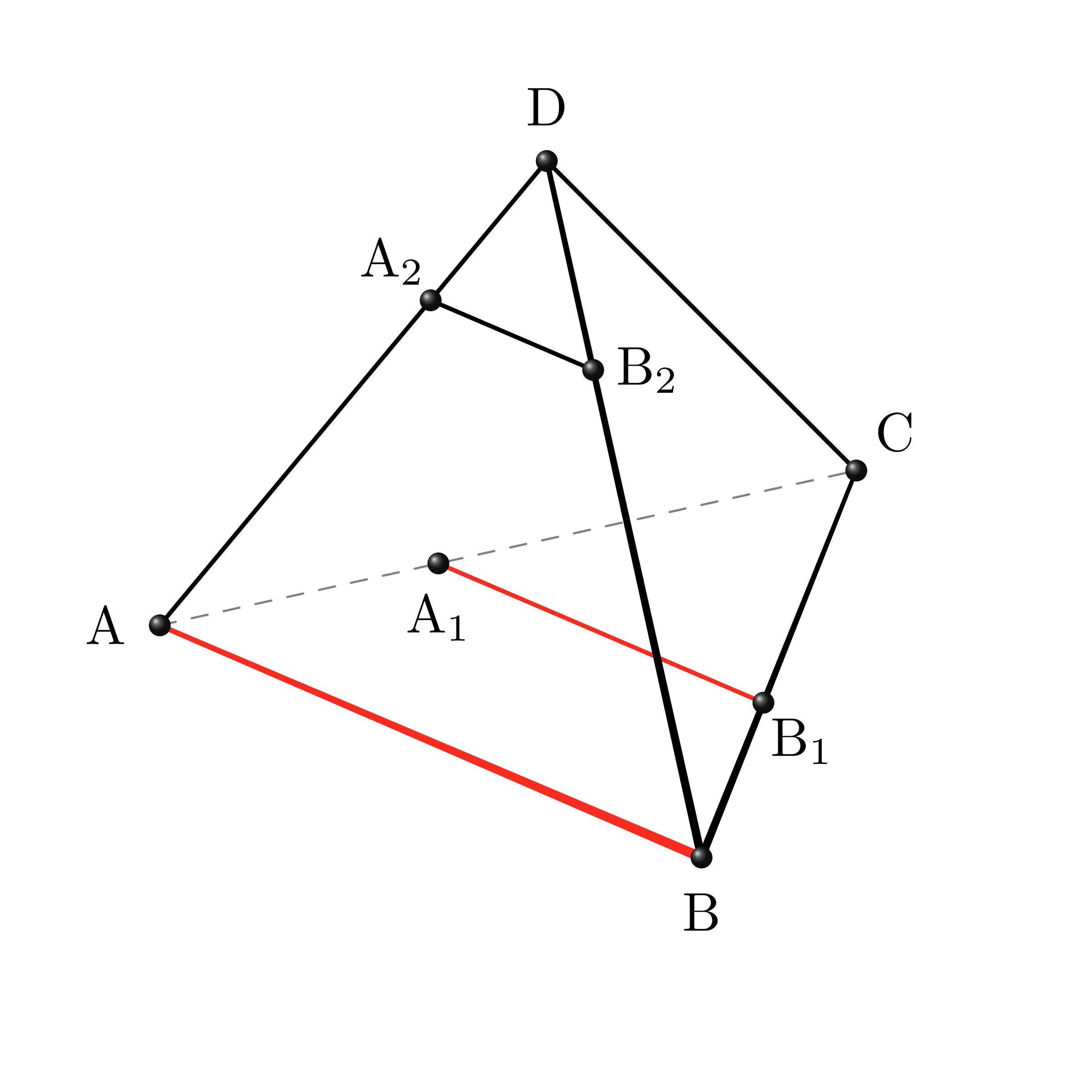
テトラ「……線分 $\AiBi$ は辺 $\AB$ と平行であることを示せ」
図を描きながら問題を読む（５）：……線分 $\AiBi$ は辺 $\AB$ と平行であることを示せ。
僕「……」
テトラ「先輩？」
僕「あ、ごめん。 テトラちゃんが一歩一歩ていねいに図を描きながら問題を読んでいくのに引き込まれてしまった。 図を描くのは、問題を解くテクニックとしての意味だけじゃなくて、 もっと大事な意味がありそうだなあ——って思ってたんだよ。 図形を実際に操作するみたいな意味」
テトラ「先輩のおっしゃりたいこと、何となくわかります。 図を描きながら読み進めると、 問題の言ってる内容があたしの心の中にすうっと入ってくるような感じがしますから。 それから図形に触れているような感じもします」
僕「うんうん」
テトラ「たとえば『辺 $\AD$ の上に点 $\Aj$ をとる』というときには、 まず辺 $\AD$ をすうっと指でなぞって、それからその途中に点 $\Aj$ を置く……みたいに」
僕「なるほどね」
テトラ「文章だけを読んでいると、 最初はいいんですけど、文字が増えていくにつれて、だんだんモヤモヤしてきます。 『えっと、点 $\Aj$ はどこにあるんでしたっけ？』となって、 文章を読み返したりすることになるからです。 でも図を描くと実際に指でなぞってから置いた手触りが残っているので 『点 $\Aj$ はここにある』とわかりやすくなるのかもしれませんね」
僕「確かに、確かに」
テトラちゃんは、自分の感覚を言葉に乗せるのがうまいなあ。
僕が何となく感じたことを、すっと言語化してくれる。
テトラ「はい、ここまで図を描きながら問題を読んできました」
僕「ところで、補足説明に入っている 『この四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ は一つの平面上にはなく、 どの三点を選んでも一直線上にはない』の意味は伝わってる？」
問題2（再掲、図が描けた。補足説明を強調）
四面体 $\TT{ABCD}$ がある。
なお、 四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ は一般の位置にある。 すなわち、この四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ は一つの平面上にはなく、 どの三点を選んでも一直線上にはない。
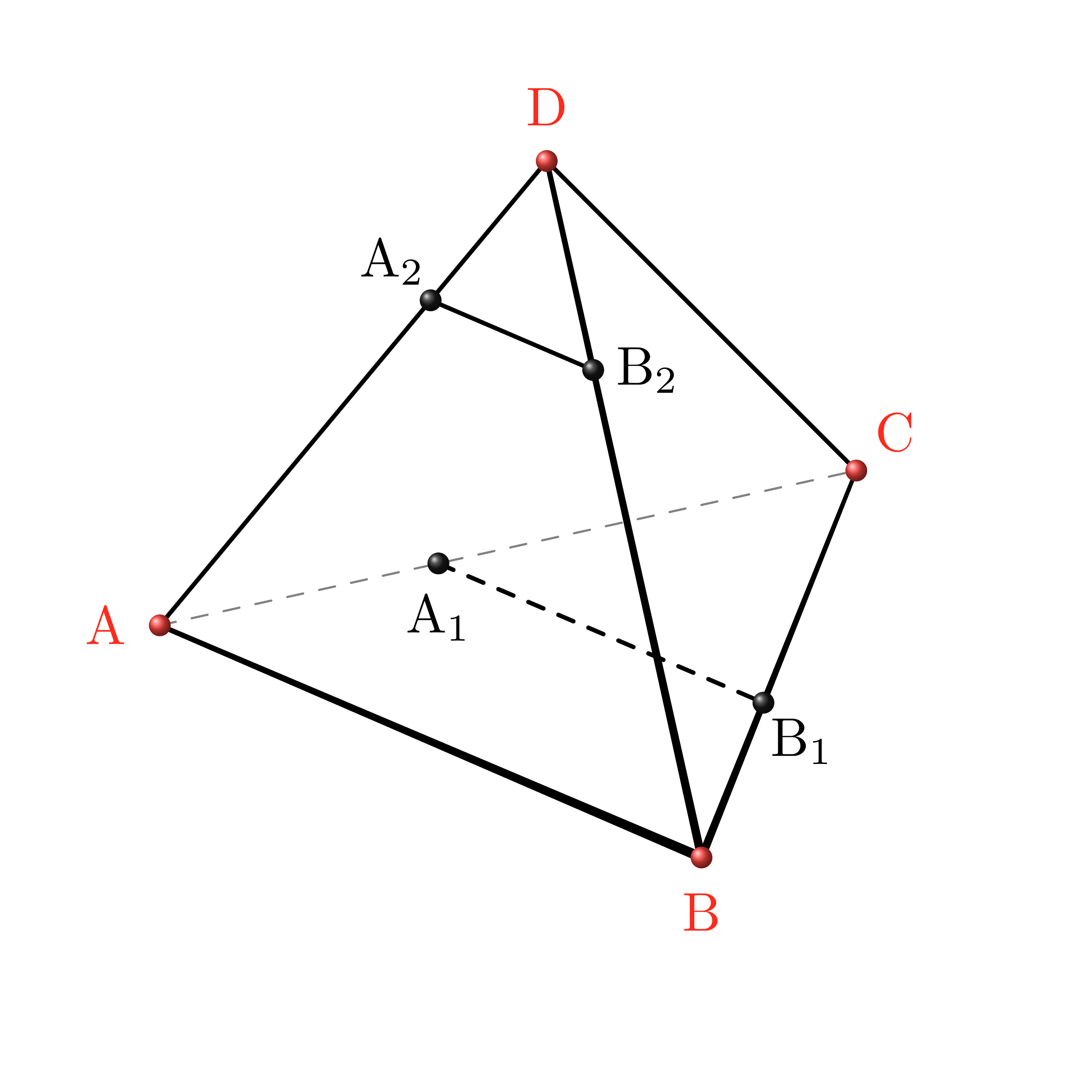
テトラ「え？ あ、はい。 わかっています。 $\TT{A},\TT{B},\TT{C},\TT{D}$ の四点は、 こう……バラバラの位置にあるということですよね」
僕「そうだね。だからこの問題2は空間で考える問題ということになる」
テトラ「はい、わかります。 ところで、この図を見ていると、 スパッと切りたくなりますよね」
僕「切る？」
テトラ「はい。 $\AiBi$ と $\AjBj$ が平行ということは、 ええと、ねじれていないので、 四点 $\Ai,\Bi,\Aj,\Bj$ を通る平面でスパッと切れそうだな、と思ったんです」
四点 $\Ai,\Bi,\Aj,\Bj$ を通る平面
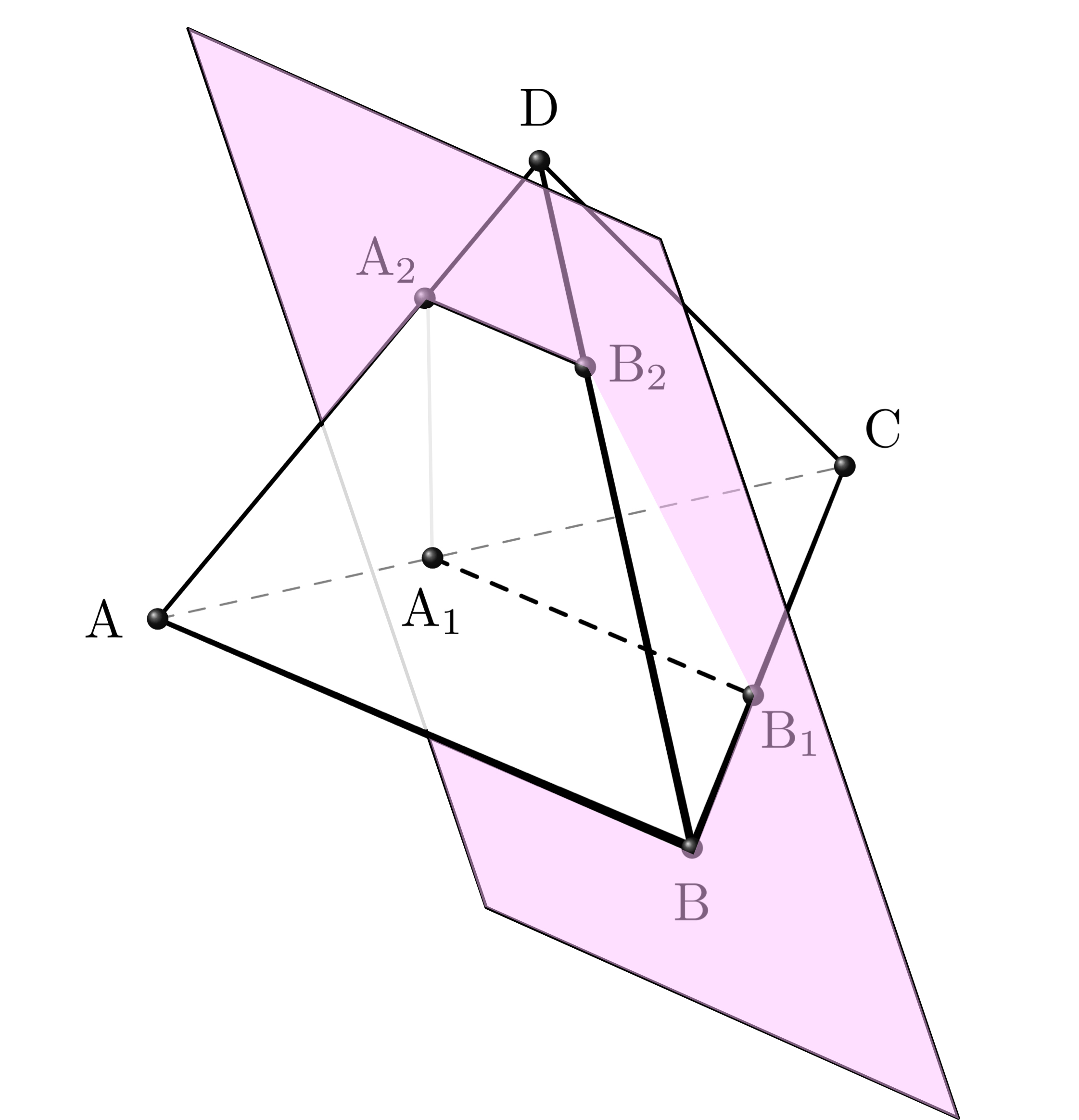
僕「ああ、そういうこと……」
テトラ「そして、その平面が $\AB$ と平行になるのかしらん……と思ったんですが、 でもそれを証明せよと言われても、どう考えていいのかわかりません」
テトラちゃんは図を指さしたり、 両手と腕をくねくねと回したりして、 自分のイメージを説明する。 まるでダンスかマジックを披露しているみたいだ。
僕「平面で切るというのはおもしろいけど、 必ずしも $\AiBi$ と $\AjBj$ が平行でなくても、 その平面は生まれそう」
テトラ「？」
僕「確かに、 $\AiBi$ と $\AjBj$ が平行だったらねじれの位置にないので、一つの平面を決める。 でも、 $\AiBi$ と $\AjBj$ が平行でなくても、たとえば『ハの字』みたいになっていても平面は決まるから、 僕たちが《求めたいもの》に、すぐにはつながらないように思うんだ。いや、よくわからないけど」
テトラ「《求めたいもの》というのは《$\AiBi$ は $\AB$ と平行である》のことですよね」
僕「そう」
テトラ「……」
テトラちゃんは無言になって考え始めた。
もちろん、僕は無言で待つ。 僕はこの問題2を以前解いたことがあるから、 証明の流れも大事なポイントもわかっている。
でも、彼女が自分で考えているときにあれこれヒントを出すわけにはいかない。
僕が先回りしてヒントを出してしまったら、 テトラちゃんが考える喜びを台無しにしてしまう。
自分で考えを巡らせることは——たとえ解決まで至らないとしても——非常に重要なのだ。
僕「……」
テトラ「……やはり、ベクトルを使ってみようかと思います。 うまく補助線のようなものを見つければ図形的に証明できるのかもしれませんけれど」
僕「もちろん、証明するときにはどんな方法でもいいんだよ」
テトラ「はい。でもいま考えてみたんですが、 ベクトルを使えば、最初のとっかかりができそうだなと思いました。 たとえば『$\AiBi$ と $\AjBj$ が平行である』という条件は、 $$ \vAiBi = k\vAjBj $$ のように表せますよね。 $k$ という新たな文字が出てきちゃいますけど」
僕「うん。あ、ただし $k \NEQ 0$ になるかな。 《$\AiBi$ と $\AjBj$ が平行である》は《ある実数 $k \NEQ 0$ に対して $\vAiBi = k\vAjBj$ が成り立つ》がいえる」
テトラ「$k = 0$ だと $\vAiBi = \vZ$ になって $\Ai$ と $\Bi$ が同じ点になってしまうから」
僕「そういうこと」
テトラ「では、問題2に与えられた条件をベクトルを使った式に落とし込んでいくことにします。 これは、またまた、たくさんの文字が出てくるはずですが《腕力》でがんばりますっ！」
問題2（再掲）
四面体 $\TT{ABCD}$ がある。
なお、 四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ は一般の位置にある。 すなわち、この四点 $\TT{A},\TT{B},\TT{C},\TT{D}$ は一つの平面上にはなく、 どの三点を選んでも一直線上にはない。
テトラちゃんはせっせと式に落とし込んでいく。
僕「できた？」
テトラ「はいっ、こんなふうにまとめてみました」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2024年11月1日）
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)