![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ここは僕の高校。いまは放課後。
僕がいつものように図書室に行くと、 後輩のテトラちゃんが問題に向かっていた。
僕「今日はどんな問題? あ、村木先生の新作だね?」
テトラ「先輩、ちょうどいいところに! いまこの《カード》を研究し始めたところですっ!」
テトラちゃんは、そういって村木先生からやってきた《カード》を見せた。
村木先生の《カード》
村木先生は、僕たちの数学教師。
ときどき、謎めいた《カード》をくれる。
そこには数学の問題が書かれていたり、 数式がポツンと書かれていたり、 図形や意味ありげなパターンが描かれていたりする。 《カード》に何も描かれていない場合すらある。 不思議な封筒をもらったこともあったなあ(第293回参照)。
ともかく、僕たちはそれをきっかけにして、 数学を考え始める。 問題が書かれていたらそれを解こうとする。
問題が書かれていなくてもかまわない。 問題がなくても、 そこに提示されている《何か》から自由に発想して《おもしろいこと》がないかを考える。 そして自由に《数学トーク》を繰り広げる。
問題が書かれているかどうかは重要じゃない。 書かれていた問題を解いた後でも、 どうせ『ここからさらに何か《おもしろいこと》は見つからないか』を考えるんだから。
《カード》をきっかけにはするけれど、 僕たちの《数学トーク》は自由なのだ。
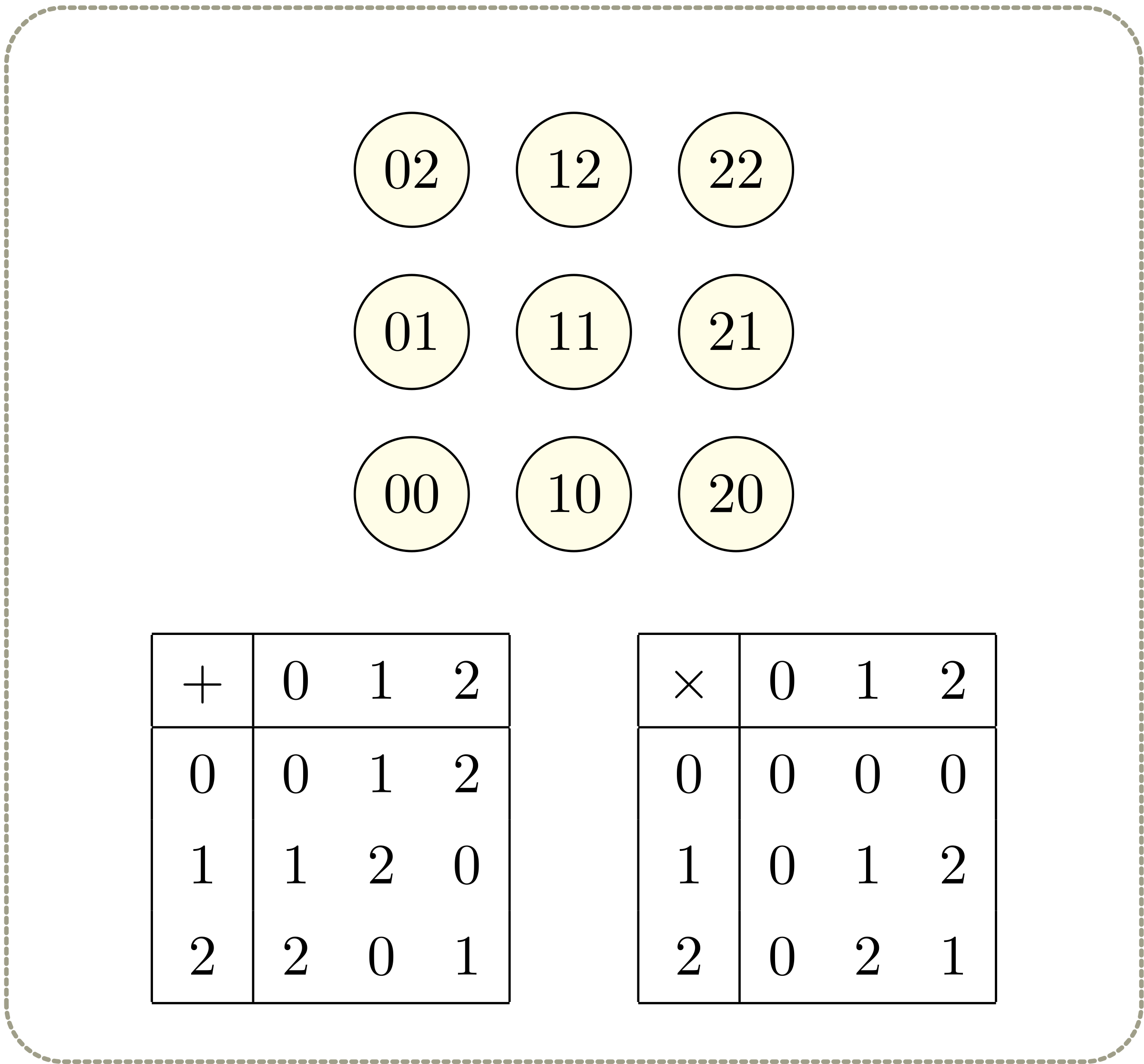
僕「九つのコインみたいなものがあって、 $$ 02,12,22,01,11,21,00,10,20 $$ と数字が描かれているね」
九つのコイン
テトラ「はい。それから下の方には演算表らしきものがあります。 足し算と掛け算です」
足し算と掛け算の演算表
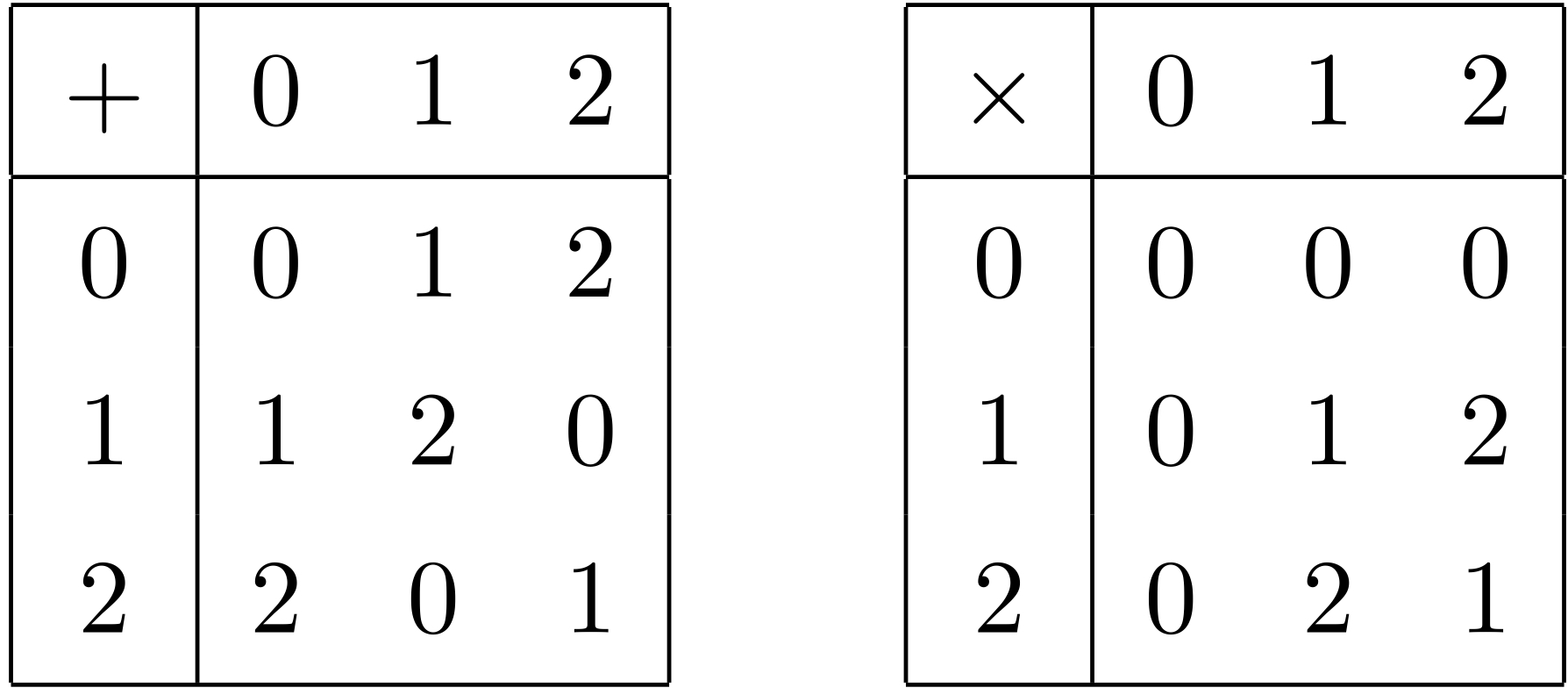
僕「ああ、この演算表はわかるね」
テトラ「はい。ふつうに計算をして、 $3$ 以上になったら、 $3$ を引き算するんですね。 たとえば、 $2 + 1 = 3$ ですけど、 $3$ 以上になったので $3$ を引いて $0$ にする。 それから、 $2 \times 2 = 4$ ですけど、 $3$ 以上になったので $3$ を引いて $1$ にする」
僕「そうだね。同じことだけど《$3$ で割った余り》の計算。 $0,1,2$ だけの文字しかない《時計演算》ともいえる」
テトラ「このコインで三進法の計算ができますね」
僕「三進法の計算? うーん、その場合には繰り上がりが必要だよね。 この表には繰り上がりがないよ。 三進法じゃなくて、こういう桁ごとの計算になるんじゃない?」
演算表を使ったコインの計算の例(繰り上がりなし)

テトラ「なるほど、左桁と右桁をそれぞれ個別に計算するんですね」
僕「自由に考えているんだから、 別に正解があるわけじゃない。 好きに決めていいんだけどね……」
テトラ「はい」
そこで僕は、あることに気付いた。
僕「ねえ、テトラちゃん、もしかして村木先生に ベクトル のレポートを何か出した?」
僕たちは《数学トーク》の内容をレポートにまとめて、村木先生に見てもらうことがある。 それは、数学の成績のためにやっているんじゃない。 楽しいからやっているんだ。
テトラ「え? はいはい、出しましたよ。 ユーリちゃんと先輩が考えていたメネラウスの定理とベクトルのこと(第432回参照)や、 図形の証明をベクトルで行った話(第435回参照)を簡単にまとめて先生に渡しました」
僕「なるほどね。それでこの《カード》が来たんだよ」
テトラ「はい?」
僕「村木先生はこのコインをベクトルに見立てたんじゃないかな」
テトラ「コインがベクトル?」
コインがベクトル?

僕「そうだね。いや『ベクトルに見立てた』というのは変かな。 『ベクトルと見なした』とか……まあ、言い方はさておき、ベクトルにできるよ。 だって、ほら、二桁の数を $x$ 座標と $y$ 座標だと思えば、コインは《座標平面の点 $(x,y)$》になる。 ただし、 $0,1,2$ の三つの数しか出てこないから、 $3 \times 3 = 9$ で《九つの点しか存在しない平面》ができあがるね」
テトラ「ええと?」
僕「コインに描かれた $$ \begin{array}{ccc} 20 & 21 & 22 \\ 10 & 11 & 12 \\ 00 & 01 & 02 \end{array} $$ という数字がある。この数字で、
テトラ「なるほど」
僕「$9$ 個の点だけでできた平面だから、いわば《九点平面》ができるんだね!」
テトラ「九点平面!?」
《九点平面》
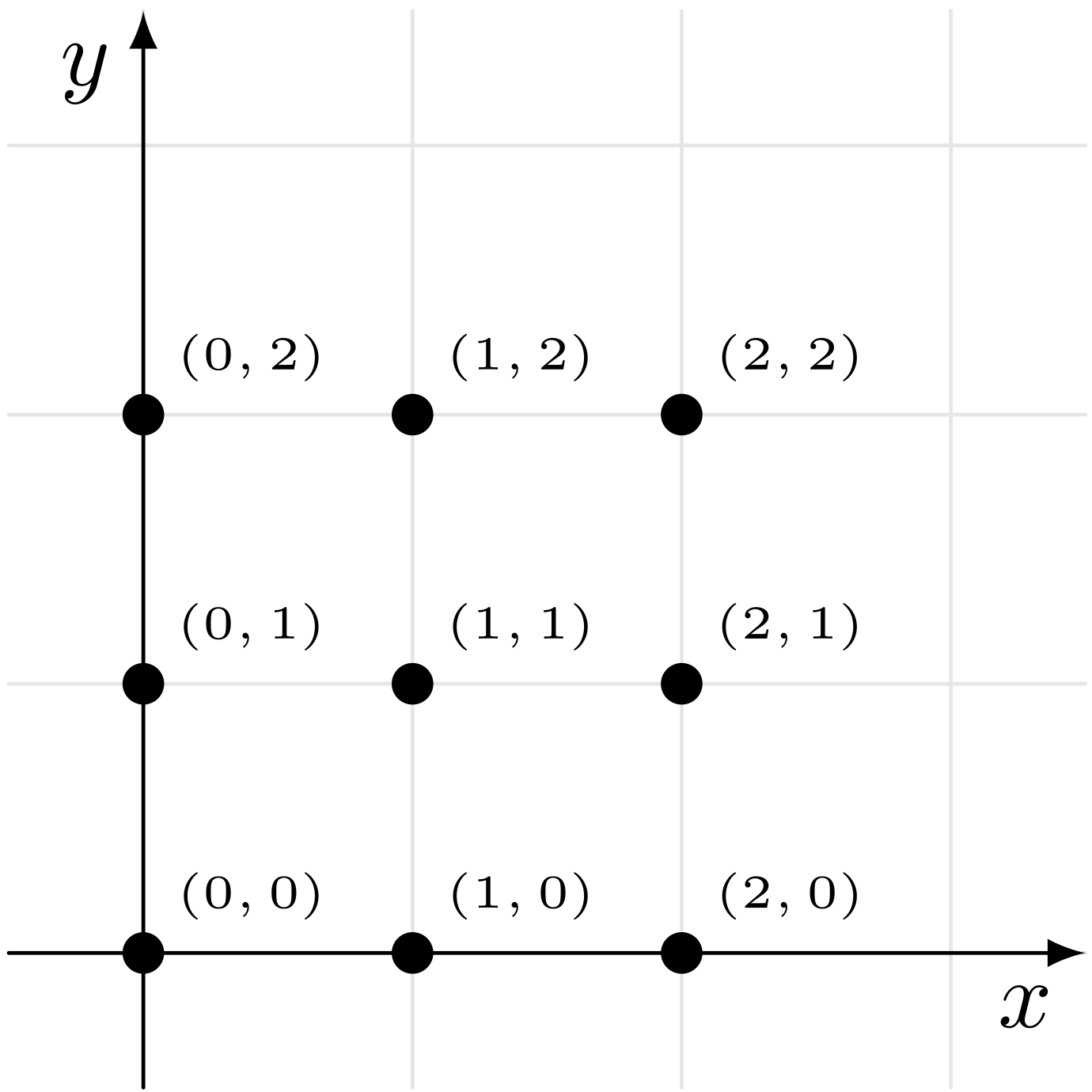
僕「座標平面で考えれば、 ふつうの矢印ベクトルと同じように計算ができる。 《九点平面》でもベクトルの和が計算できるわけだ」
テトラ「ベクトルの和……ああ、こういうことですね。 たとえば、 ベクトル $(1,0)$ と $(1,1)$ の和なら、 $$ (1,0) + (1,1) = (2,1) $$ のようになる?」
ベクトル $(1,0)$ と $(1,1)$ の和は $(2,1)$
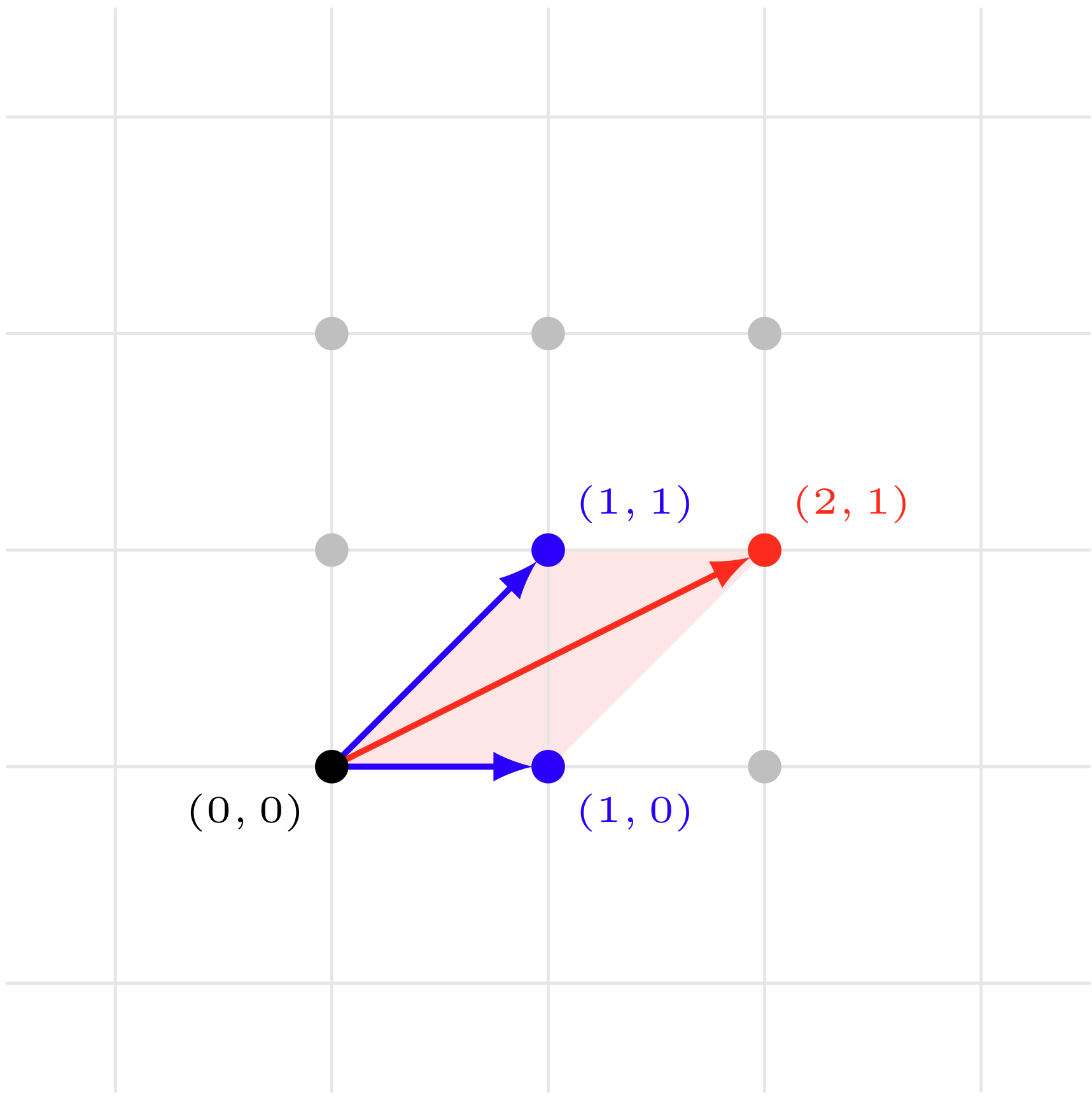
僕「うん、そういうこと。 さっき《左桁と右桁を個別に計算する》といったけど、 それは矢印ベクトルを座標平面に 描いたときに《$x$ 成分と $y$ 成分を個別に計算する》ことに対応しているわけだね」
テトラ「わかります」
僕「ああ、成分ごとに計算するなら縦ベクトルで書いた方が便利だね。 ベクトル $\VECV10$ と $\VECV11$ の和なら、 $$ \VECV10 + \VECV11 = \VECV21 $$ になる」
ベクトル $\VECV10$ と $\VECV11$ の和は $\VECV21$ (縦ベクトルで表記)
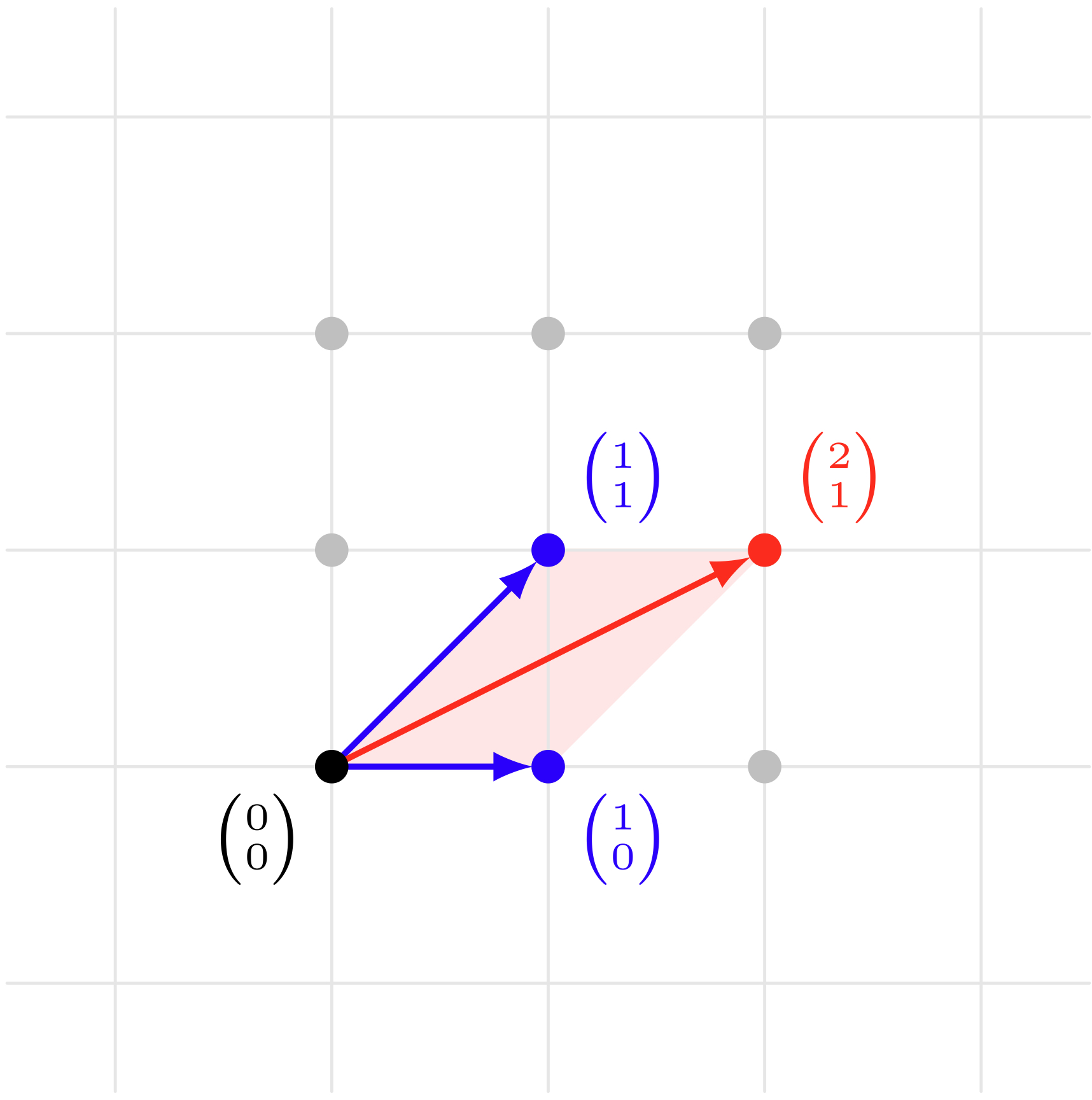
$$ \VECV10 + \VECV11 = \VECV21 $$
テトラ「なるほど。縦ベクトルだと、計算する成分が同じ高さに並ぶから計算しやすいということですね。 たとえば、 $$ \VECV21 + \VECV01 = \VECV22 $$ なら、 $$ \begin{cases} 2 + 0 &= 2 && \REMTEXT{$x$成分} \\ 1 + 1 &= 2 && \REMTEXT{$y$成分} \end{cases} $$ となりますから」
僕「そうだね」
ベクトル $\VECV21$ と $\VECV01$ の和は $\VECV22$
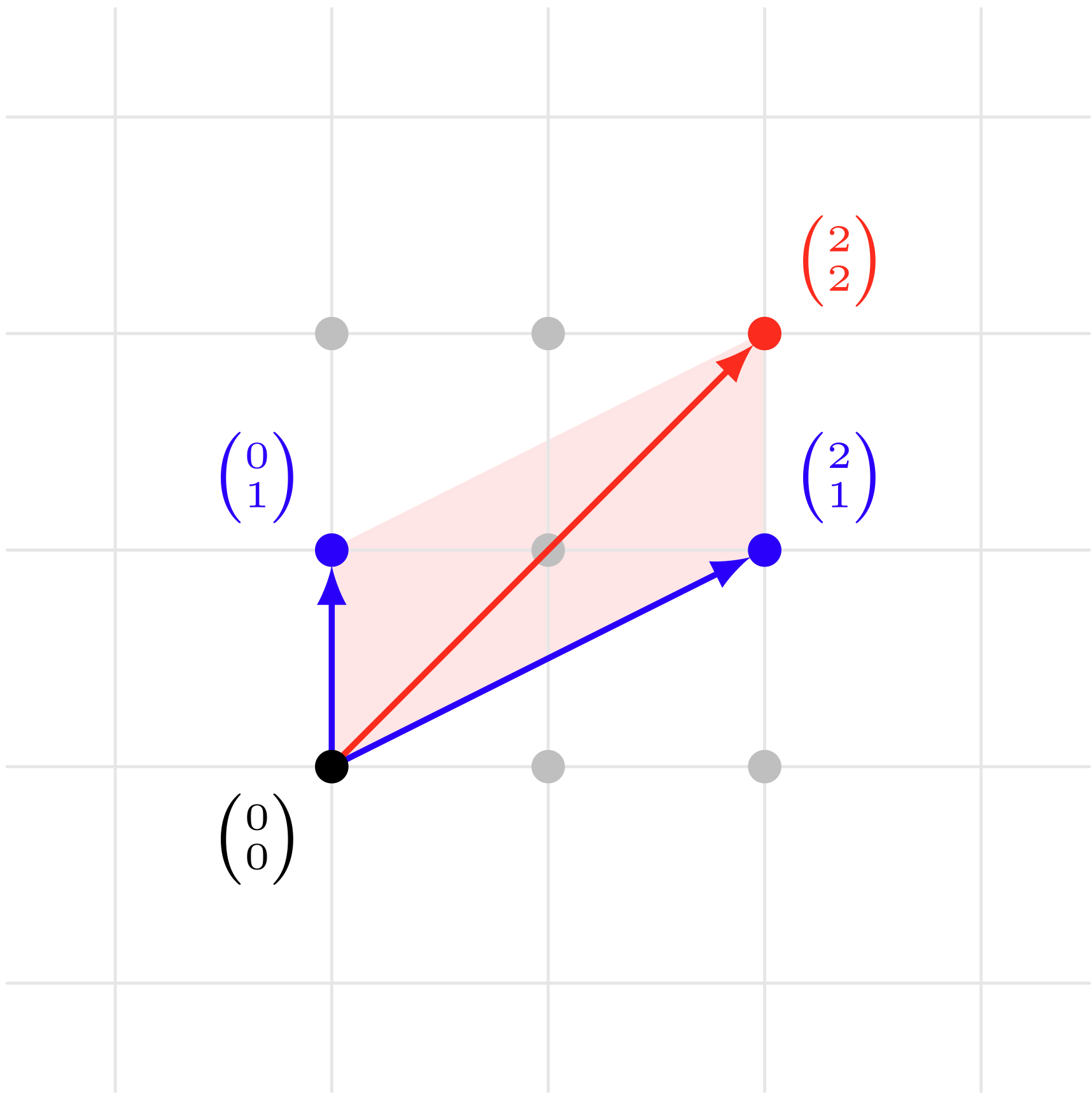
$$ \VECV21 + \VECV01 = \VECV22 $$
テトラ「はい。成分ごとに足し合わせればいいですね……あらら、ちょっと待ってください。 《九点平面》の演算表はどう考えたらいいですか?」
僕「……」
足し算と掛け算の演算表(再掲)

テトラ「$\VECV10 + \VECV11 = \VECV21$ や $\VECV21 + \VECV01 = \VECV22$ については、 $3$ 以上になる成分が出てこなかったからいいですけど、 たとえば、 $$ \VECV20 + \VECV12 = \cdots $$ を考えてみますと、 $x$ 成分が $3$ になるので $3$ で割った余りは $0$ になります。 ですから《九点平面》の世界では、 $$ \VECV20 + \VECV12 = \VECV{\REDFOCUS{0}}{2} $$ になります。 これでは、平行四辺形ができません!」
ベクトル $\VECV20$ と $\VECV12$ の和は $\VECV02$ (平行四辺形ができない?)
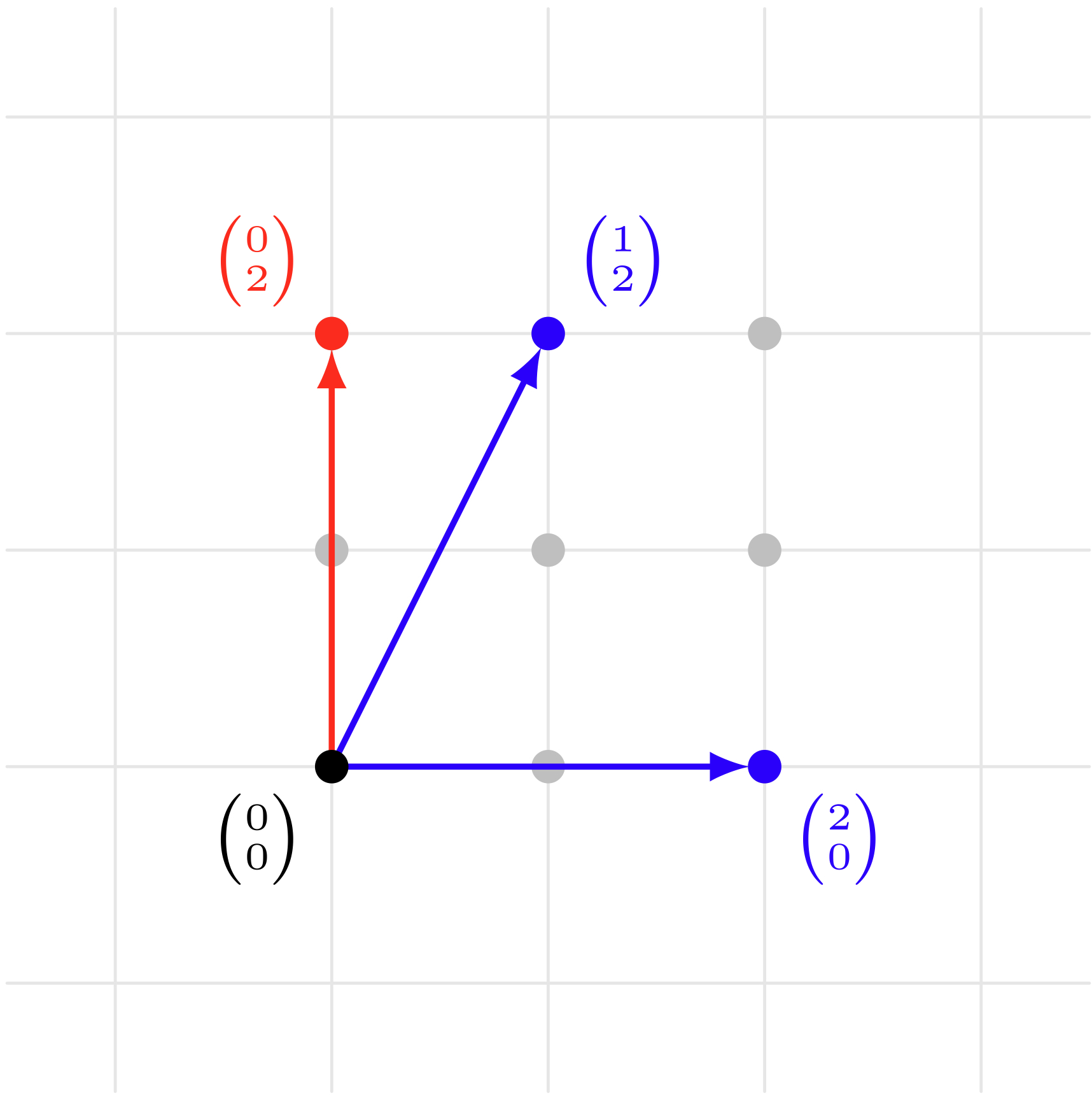
$$ \VECV20 + \VECV12 = \VECV{\REDFOCUS{0}}2 $$
僕「……」
僕は考える。
確かにテトラちゃんの主張は正しい。
もしも《九点平面》での成分計算を、村木先生の《カード》に書かれた演算表を使って行うなら、 矢印ベクトルの和に出てくるおなじみの平行四辺形は出てこなくなる。
それは確かにそうだけど……
テトラ「あ、あたし、変なことにこだわってますか?」
僕「いやいや、そんなことはないと思うよ。 テトラちゃんの主張は正しいし、平行四辺形は出てこないね。 うーん……《九点平面》の世界から離れて、もしもふつうの矢印ベクトルの和を作るなら、 こんなふうに点 $\TT{Q}\VECV32$ を頂点に持つ平行四辺形ができるはずなのに——ということだよね」
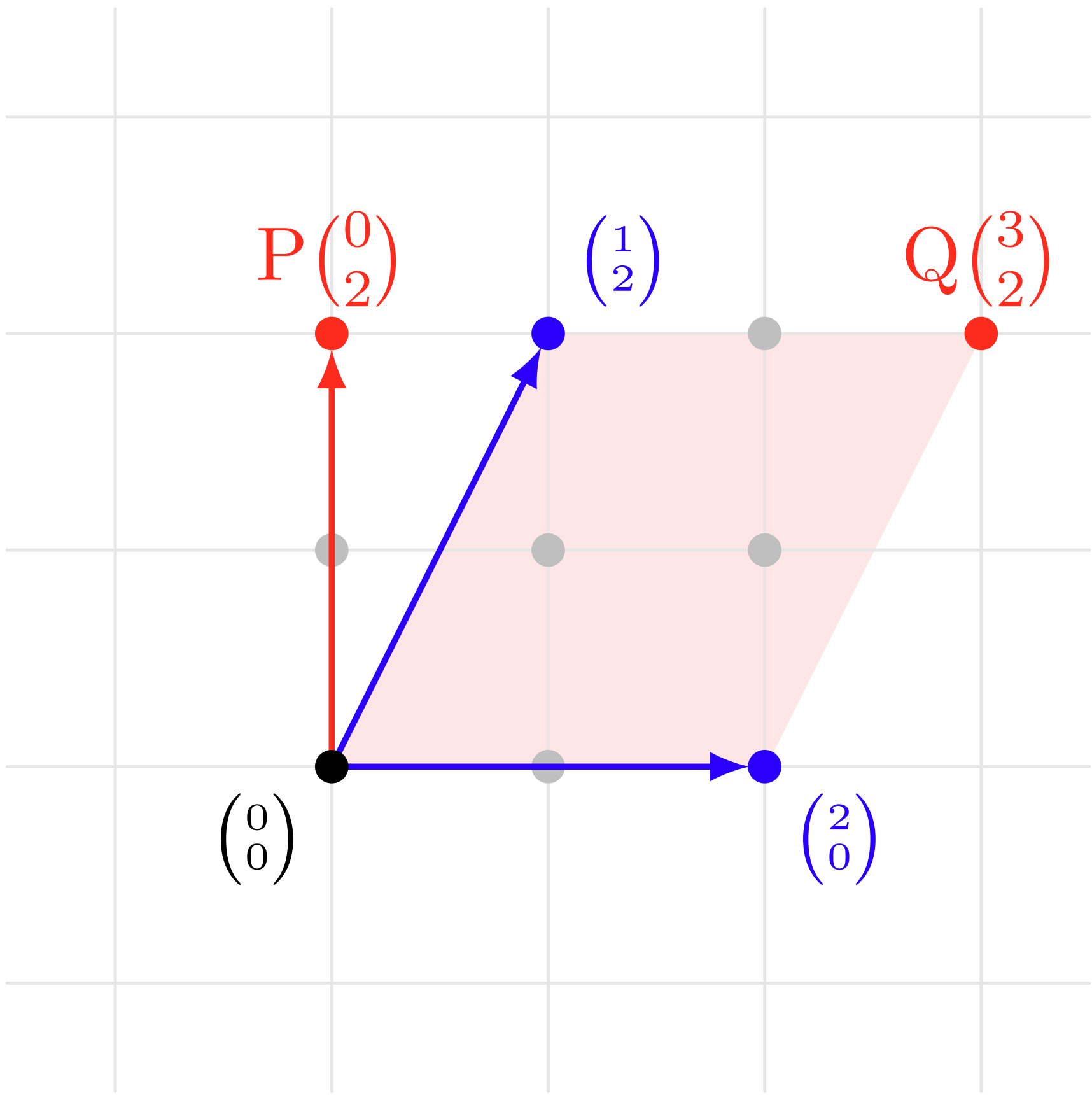
テトラ「はいはい。そういうことです。 でもこの点 $\PT Q32$ は、あたしたちの《九点平面》から飛び出しちゃってます」
僕「うーん……これは《同一視》をどう考えるかが試されているみたいだね」
テトラ「《同一視》?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年11月8日)