![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「お兄ちゃん! この問題、解ける?」
問題
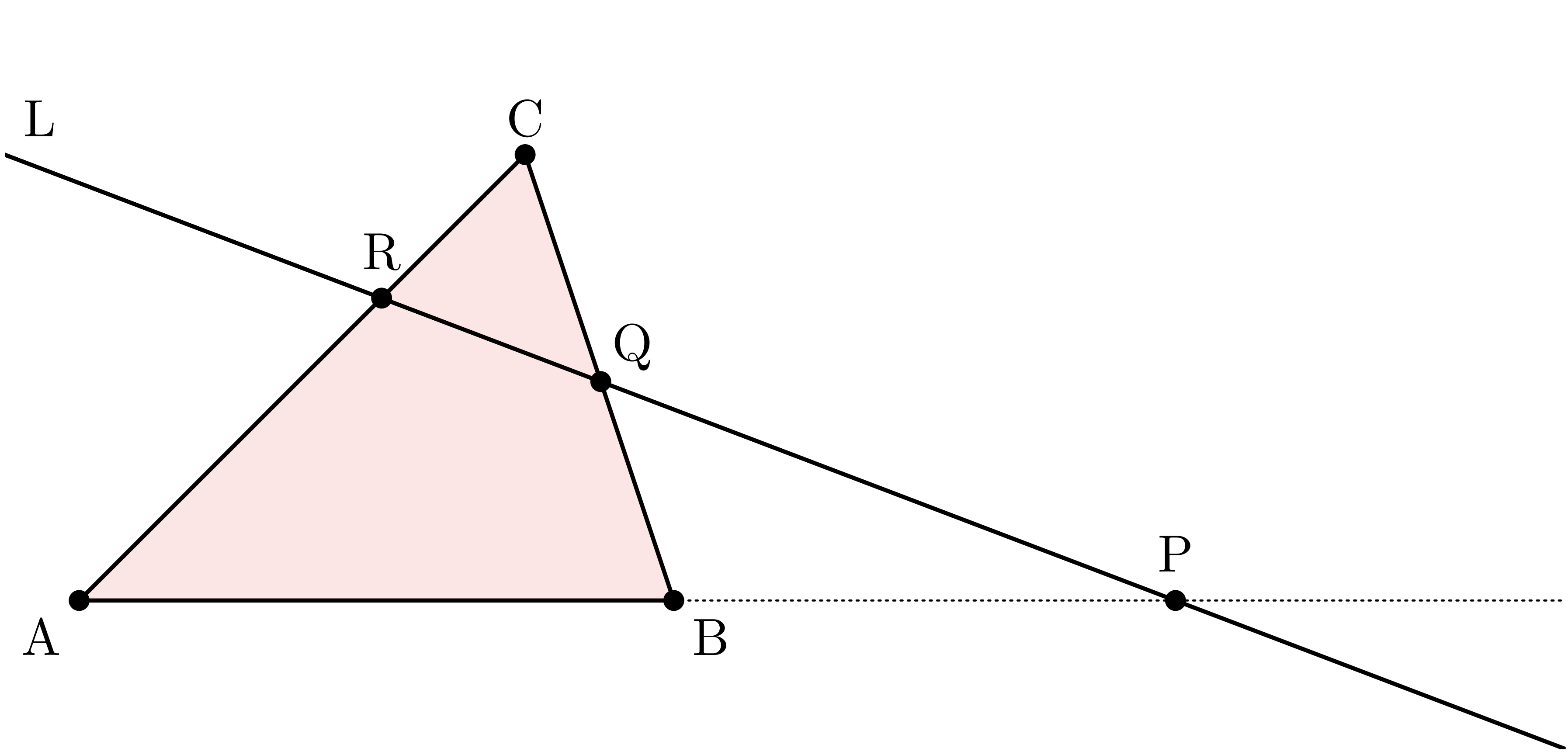
平面上に三角形 $\TT{ABC}$ がある。
また図のように、 辺 $\TT{BC}$ と辺 $\TT{CA}$ に交わる直線 $\TT{L}$ がある。
このとき、
$$ \frac{\TT{AP}}{\TT{PB}} \times \frac{\TT{BQ}}{\TT{QC}} \times \frac{\TT{CR}}{\TT{RA}} $$
の値を求めよ。
※この式で、たとえば「$\TT{AP}$」は「線分 $\TT{AP}$ の長さ」を表しているものとします。 また「線分 $\TT{AP}$ の長さ」は「$\BAR{\TT{AP}}$」のように上線を付けて表すこともあります。
僕「今シーズンのユーリはやって来るなり、いきなりの問題かい」
ユーリ「いきなりのメタ発言自重! ちゃんと考えて解いてよ!」

僕「はいはい……っと。 問題の式に出てきた $$ \frac{\TT{AP}}{\TT{PB}} \times \frac{\TT{BQ}}{\TT{QC}} \times \frac{\TT{CR}}{\TT{RA}} $$ をよく見ると、 ここには二本の線分が三組出てくる。 そして、組ごとに長さの比を求めて、すべて掛け合わせている。 三組というのはつまり、 $$ \begin{array}{ccc} \TT{AP} &\quad\textrm{と}\quad & \TT{PB} \\ \TT{BQ} &\quad\textrm{と}\quad & \TT{QC} \\ \TT{CR} &\quad\textrm{と}\quad & \TT{RA} \end{array} $$ だね。 図と式とを照らし合わせながら、点を順番に追っていく。
図と式とを照らし合わせながら、点を順番に追っていく
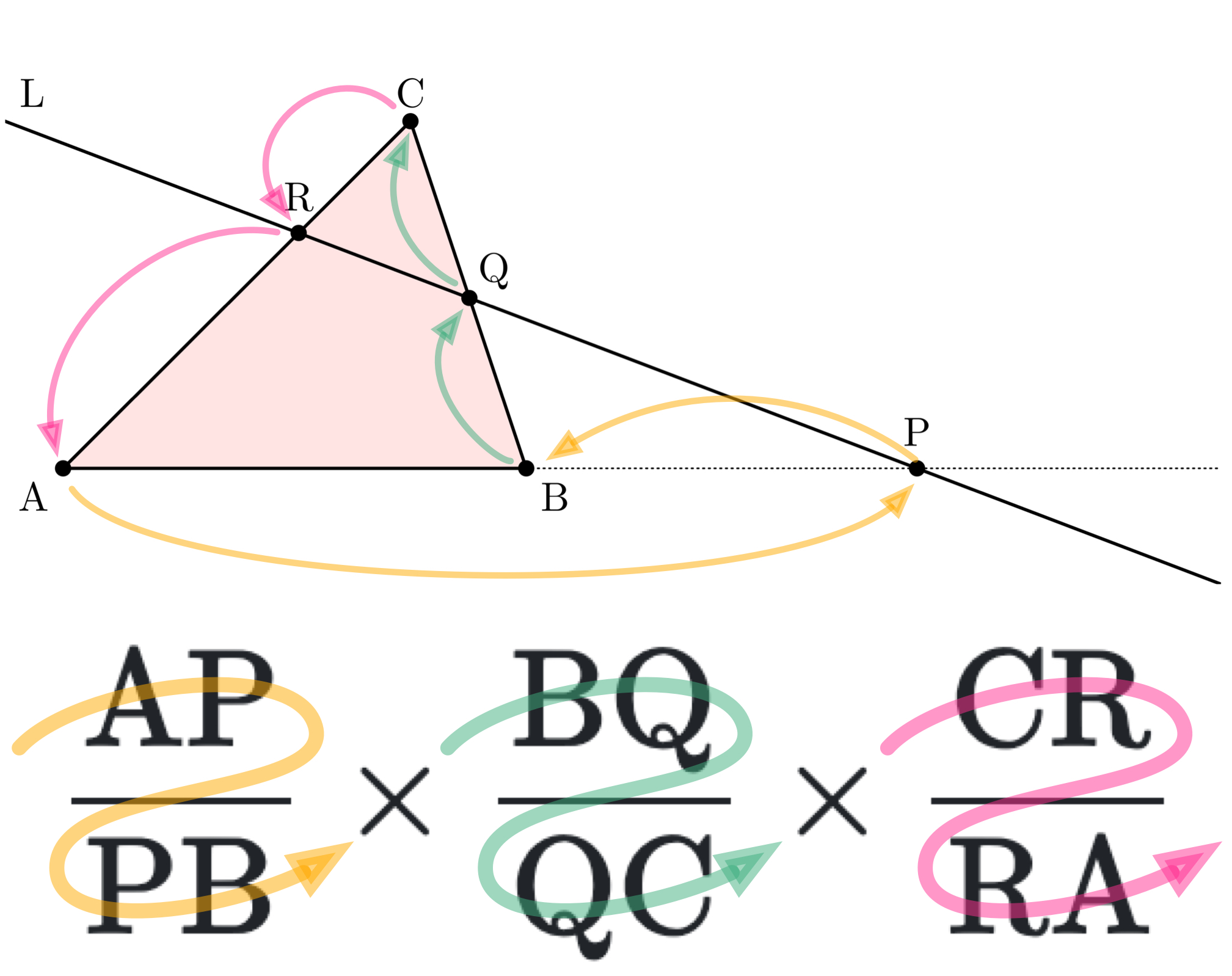
ユーリ「上がり下がり?」
僕「上がるか下がるかは大事じゃなくて、 頂点と交点を交互にたどっていくところが大事だね。
ユーリ「ふむふむ。頂点と交点がかわりばんこ」
僕「もちろんこれはメネラウスの定理を使うところだ! このとき、 三組の長さの比をすべて掛けると $1$ に等しくなるというのがメネラウスの定理だから、 $1$ が答えになるね。 メネラウスの定理を使えば一発だ。なつかしいなあ……」
解答
メネラウスの定理より、
$$ \frac{\TT{AP}}{\TT{PB}} \times \frac{\TT{BQ}}{\TT{QC}} \times \frac{\TT{CR}}{\TT{RA}} = 1 $$ である。
ユーリ「はい、正解! エピソード1は、これでおしまい。では次回のエピソード2をお楽しみに——」
僕「メタ発言自重!」
ユーリ「あのね、真面目にやろうよ。お兄ちゃん」
僕「真面目に解いたよ。メネラウスの定理。答えは $1$ で正解だろ?」
ユーリ「うん、正解は正解。 でも、それってメネラウスの定理を知ってたからだよね? そーじゃなくて、 やっぱりお兄ちゃんには、メネラウスの定理を証明してほしーなー」
僕「なるほど……メネラウスの定理の証明か。 すっかり忘れているけど、 考えればわかりそう。 うまい補助線が引ければ証明できるかな」
ユーリ「ちっちっち。そりゃ反対だよね」
僕「何が反対?」
ユーリ「《うまい補助線が引ければ証明ができる》んじゃなくて、 《証明ができるような補助線がうまい補助線》なんだよねー」
僕「ううっ……い、いや、だとしてもだよ。 うまい補助線が引ければ証明できるのは確かじゃないか」
ユーリ「そういうヘリクツはさておき、早く考えたまえ」
僕「はあ……(ためいき)」
こんなふうにして、僕とユーリのメネラウスの定理をめぐる数学トークが始まった。
ユーリ「こーゆーとき、お兄ちゃんは何から考えるの?」
僕「そりゃもちろん、メネラウスの定理のステートメントを確認するところから」
ユーリ「すてーとめんとってなに?」
僕「定理のステートメントっていうのは、 その定理が主張している内容のこと。 たいていの定理は『こういう条件ではこういうことが成り立つ』という数学的主張をしているわけだけど、 定理の証明をする前には、その定理が主張している内容を確認する必要がある」
ユーリ「内容を確認する……そんなの、あたりまえでは」
僕「うん、そうだね。あたりまえのことをきちんとやるのは大切。 だから、メネラウスの定理のステートメントを確認する。 証明を考えるのはその後」
メネラウスの定理

平面上に三角形 $\TT{ABC}$ がある。
また図のように、 辺 $\TT{BC}$ と辺 $\TT{CA}$ に交わる直線 $\TT{L}$ がある。
このとき、
$$ \frac{\TT{AP}}{\TT{PB}} \times \frac{\TT{BQ}}{\TT{QC}} \times \frac{\TT{CR}}{\TT{RA}} = 1 $$
が成り立つ。
ユーリ「それで、次は?」
僕「そうだなあ……ところで、ユーリは証明を知ってるの?」
ユーリ「カンニングするつもり?」
僕「そういうことじゃないよ」
ユーリ「一応、知ってる。ほら、お兄ちゃんがわからないときに教えてあげよーと思ってさ」
僕「それはそれは」
ユーリ「で、次は何を考えるの?」
僕「うん。 メネラウスの定理を証明するために 補助線を考えたい。 図の中にうまく補助線を引くんだ。そして、その補助線は、 相似な三角形を作るものになると思うね」
ユーリ「とつぜん、野生のお兄ちゃんが鋭いひらめきを見せた!」
僕「何だそりゃ」
ユーリ「……あのさー、お兄ちゃんって、証明覚えていないって言ってたのにさー、 何で、そーゆーのパパッと思いつくわけ?」
僕「メネラウスの定理のステートメントに出てきた、 $$ \frac{\TT{AP}}{\TT{PB}} \times \frac{\TT{BQ}}{\TT{QC}} \times \frac{\TT{CR}}{\TT{RA}} = 1 $$ という式からの想像だよ」
ユーリ「へっ? 式からの想像?」
「この式には、たとえば $$ \frac{\TT{AP}}{\TT{PB}} $$ という分数が出てくる。 これは二つの線分 $\TT{AP}$ と $\TT{PB}$ の長さの比を考えていることになるよね」ユーリ「ふむふむ。たとえば、 $$ \TT{AP}:\TT{PB} = 1:2 \quad\textrm{だったら}\quad \frac{\TT{AP}}{\TT{PB}} = \frac{1}{2} $$ とか?」
僕「そうだね。図形的に長さの比を考えるんだから、『相似な三角形が二つあったらいいなあ……』と思うわけだ。 だって、相似な二つの三角形が二つあったら、対応する辺の長さの比はすべて等しいからね。 だから、そのことをうまく使えば、 $$ \frac{\TT{AP}}{\TT{PB}} \quad\textrm{と}\quad \frac{\TT{BQ}}{\TT{QC}} \quad\textrm{と}\quad \frac{\TT{CR}}{\TT{RA}} $$ という三つの分数を、 うまいこと別の分数に置き換えられるんじゃないかと想像したんだよ」
ユーリ「にゃるほど。なかなかの名推理じゃな。 んじゃ、証明の最後まで見通しているわけじゃないということかの?」
僕「キャラおかしくなってるぞ。 もちろん、証明の最後まで見通しているわけじゃないよ。 そんなことはできないよ。 うまいこと別の分数に置き換えて、 うまいこと約分できれば、うまい具合に $1$ になるかもしれない——ぐらいは考えたけど」
ユーリ「うまいことが続けば、うまい具合に証明できるというのは、そうじゃのう……」
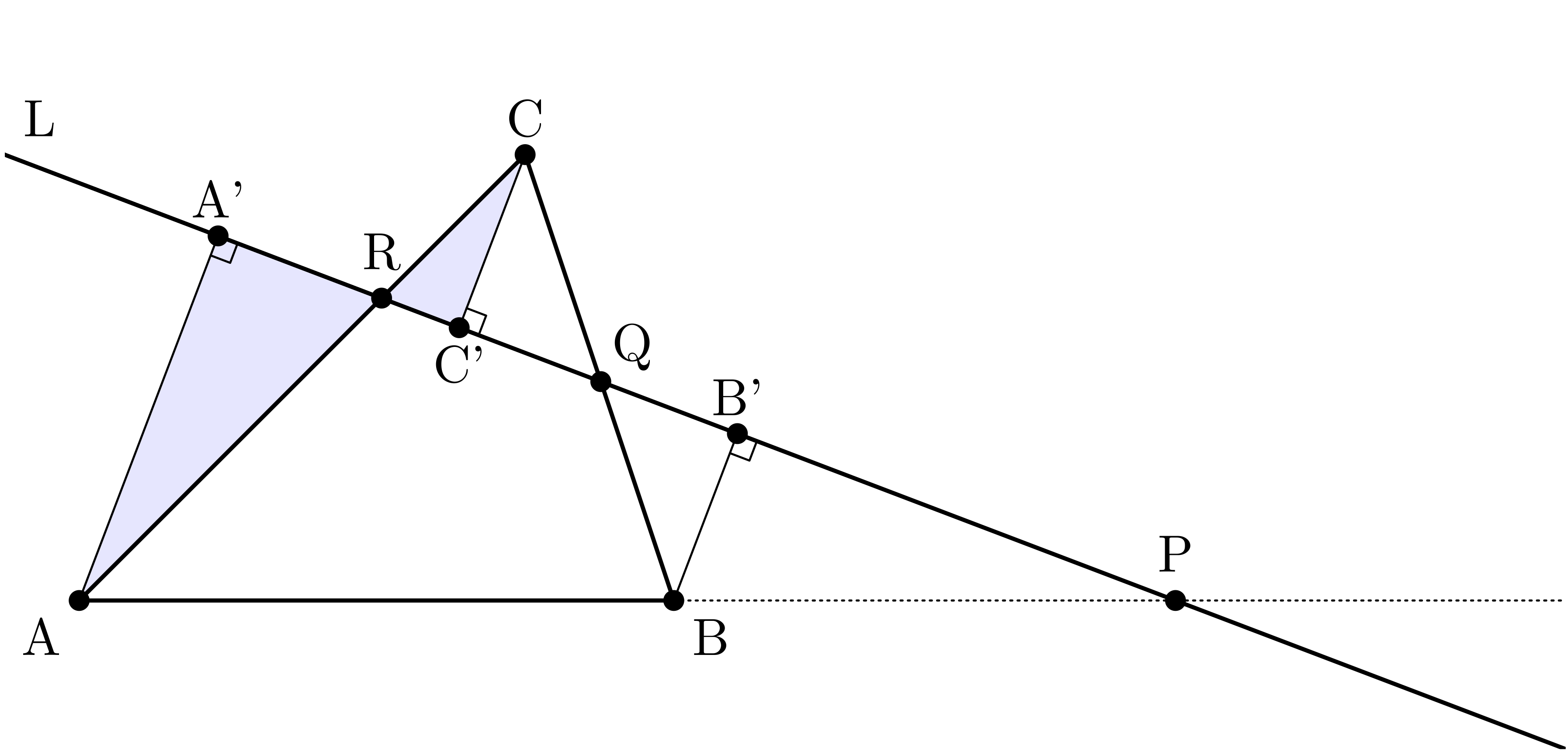
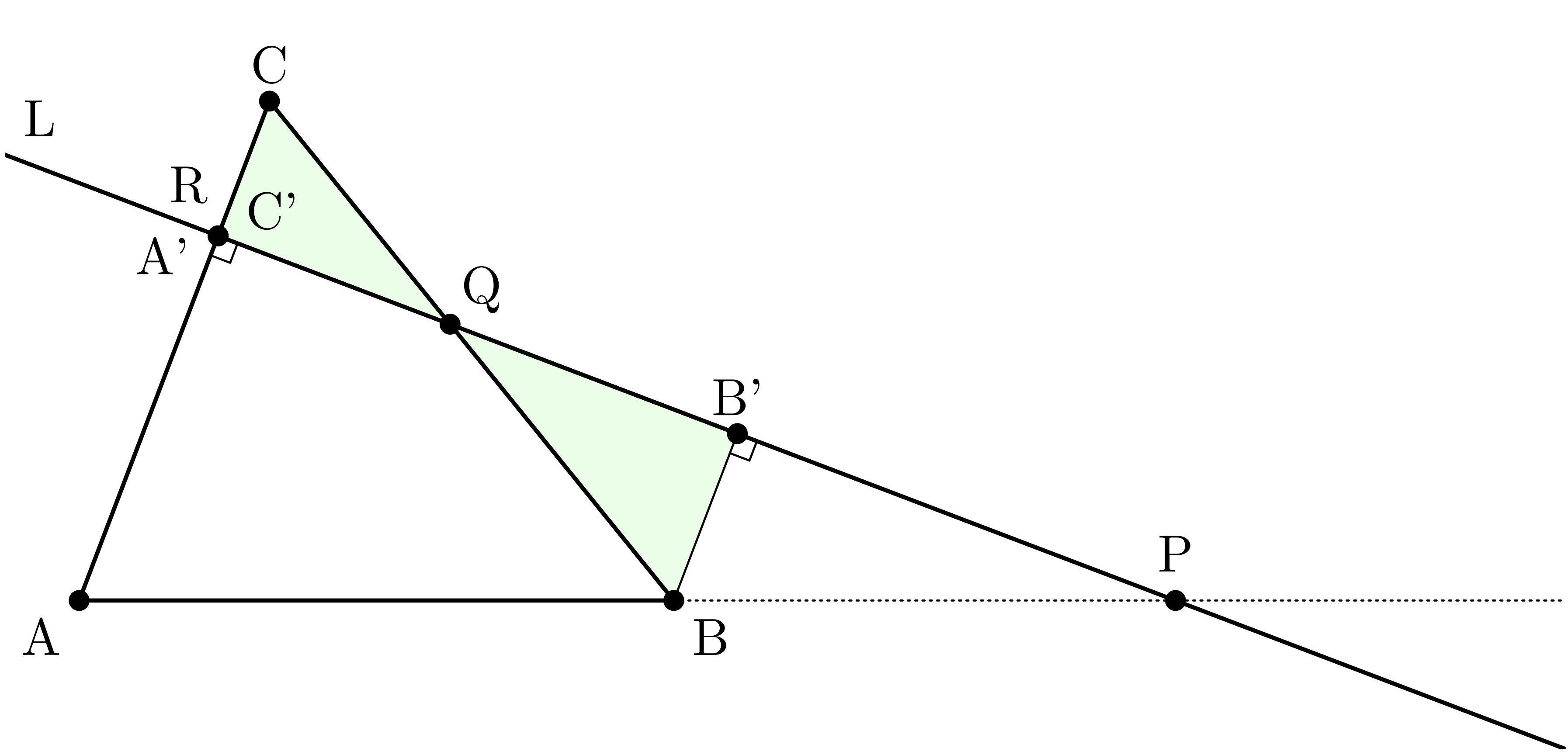
僕「だから……うん、こんなふうに、 $\TT{A,B,C}$ の各頂点から直線 $L$ に垂線を下ろすのはどうだろう。 補助線を三本引いたことになる。 そして垂線の足をそれぞれ $\TT{A',B',C'}$ とする」
僕が描いた補助線
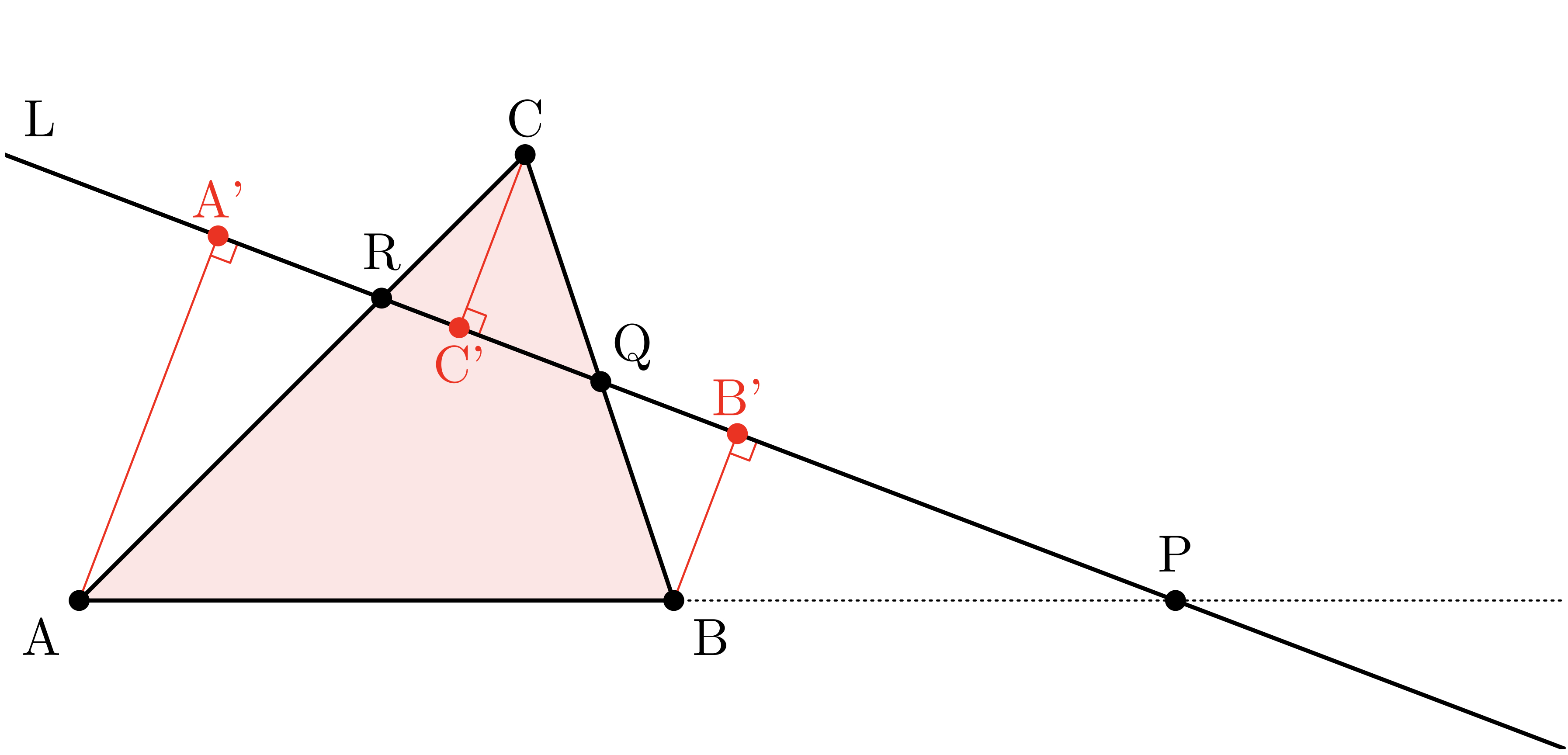
ユーリ「え、違う……」
僕「いや、これでいけるよ。ユーリが考えていた補助線とは違っているかもしれないけど、 これで証明までうまく行けるはず。 さっき考えた通り、相似な二つの三角形が三組できるから、 対応する辺の長さの比が等しいことがわかる。 これで、メネラウスの定理に出てきた式を、ぜんぶ $\TT{A'A}$ と $\TT{B'B}$ と $\TT{C'C}$ を使って表せるよ!」
$\TRI{APA'}$ と $\TRI{BPB'}$ は相似
$$ \frac{\TT{AP}}{\TT{BP}} = \frac{\TT{A'A}}{\TT{B'B}} $$
$\TRI{BQB'}$ と $\TRI{CQC'}$ は相似
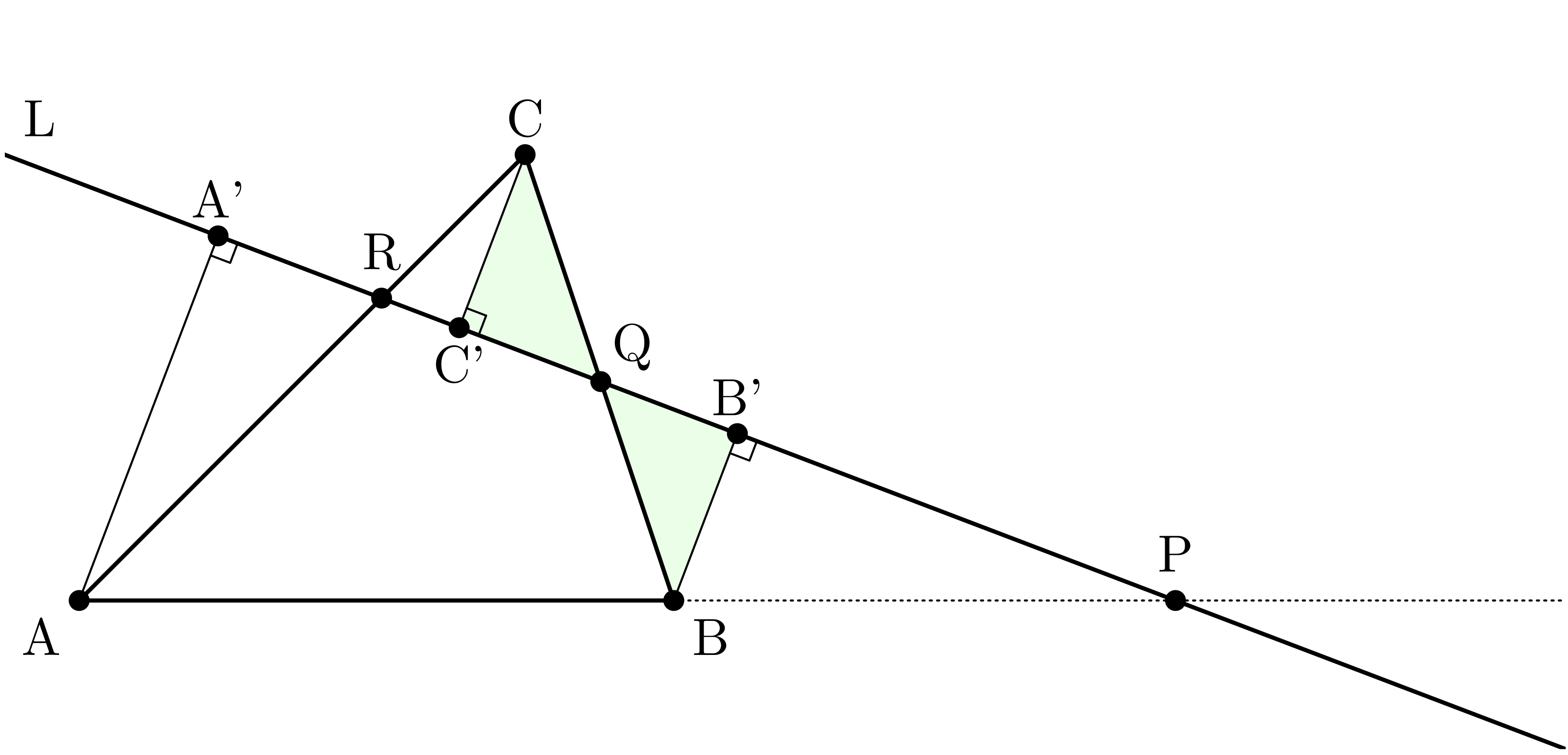
$$ \frac{\TT{BQ}}{\TT{CQ}} = \frac{\TT{B'B}}{\TT{C'C}} $$
$\TRI{CRC'}$ と $\TRI{ARA'}$ は相似
$$ \frac{\TT{CR}}{\TT{AR}} = \frac{\TT{C'C}}{\TT{A'A}} $$
ユーリ「お兄ちゃんが引いたこの補助線、ダウト!」
僕「え? 何かおかしいかな?」
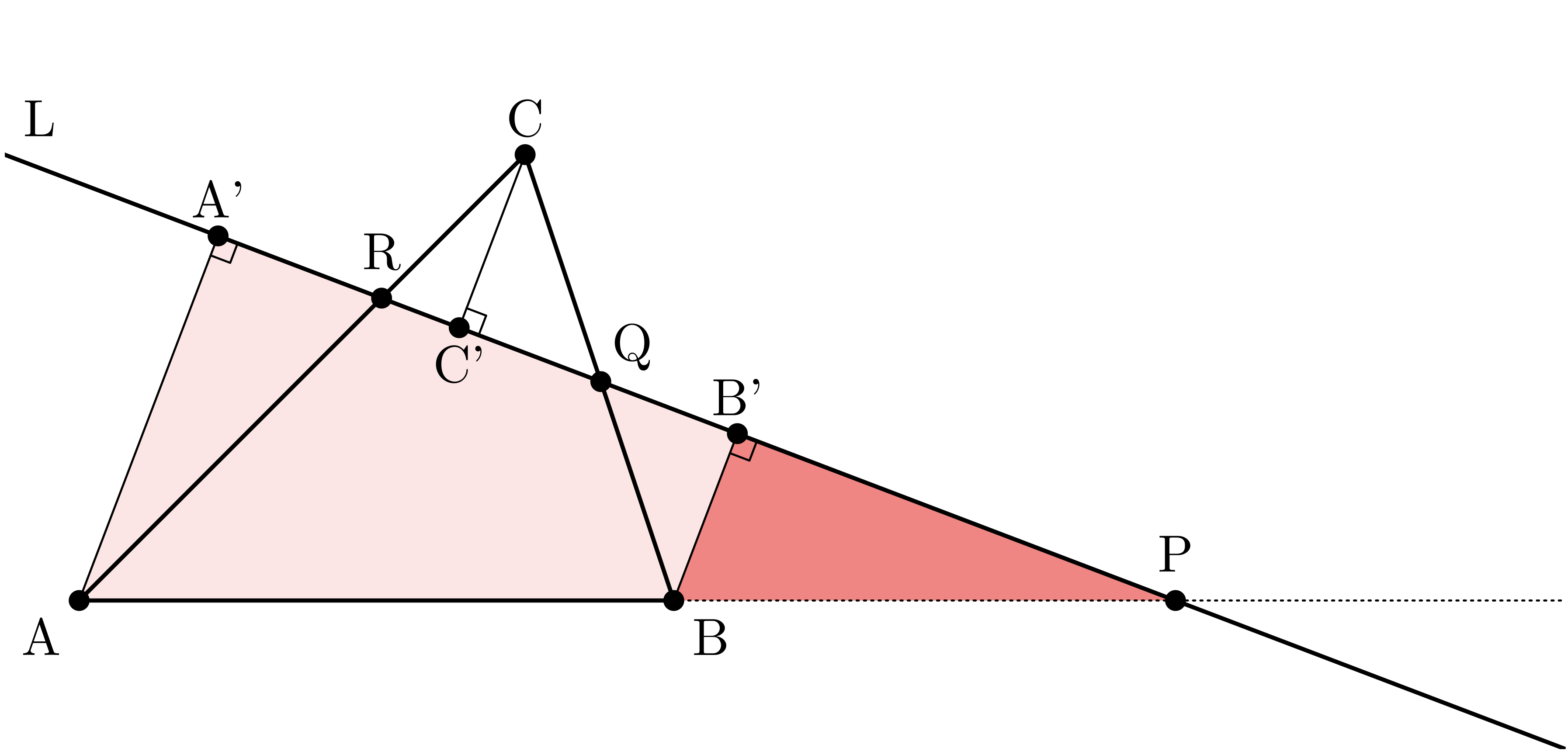
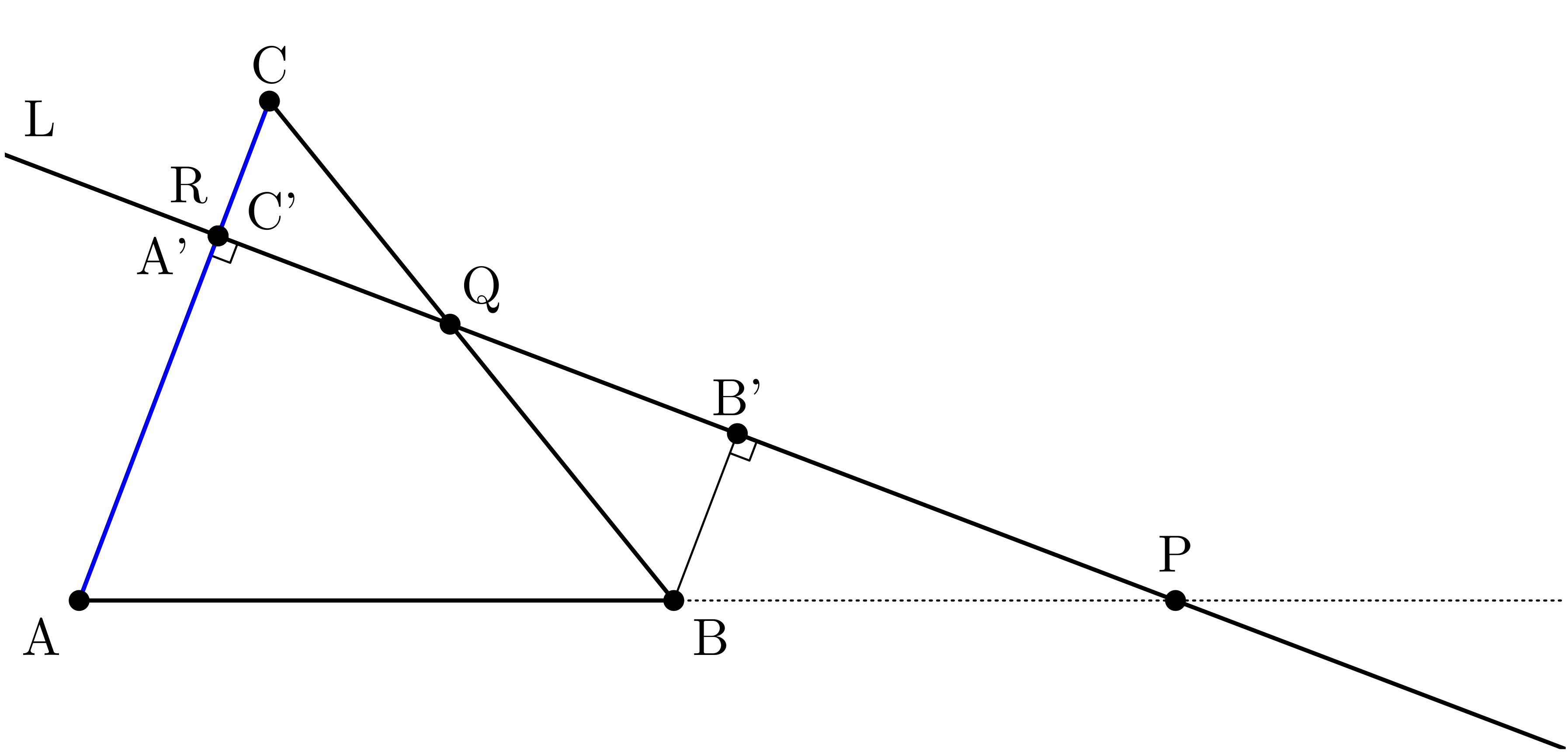
ユーリ「お兄ちゃんは $\TT{A}$ と $\TT{B}$ と $\TT{C}$ から直線 $\TT{L}$ に垂線を下ろしたけど、 もしも、辺 $\TT{CA}$ と直線 $\TT{L}$ が垂直だったらヤバいよ」
僕「辺 $\TT{CA}$ と直線 $L$ が垂直だったら——?」
ユーリ「$\TT{A'}$ と $\TT{C'}$ がどっちも $\TT{R}$ と重なるから、 三角形 $\TT{ARA'}$ と三角形 $\TT{CRC'}$ がつぶれちゃう!」
辺 $\TT{CA}$ と直線 $\TT{L}$ が垂直だったら、三角形 $\TT{ARA'}$ と三角形 $\TT{CRC'}$ が消えてしまう

$$ \textrm{↓ ↓ ↓} $$
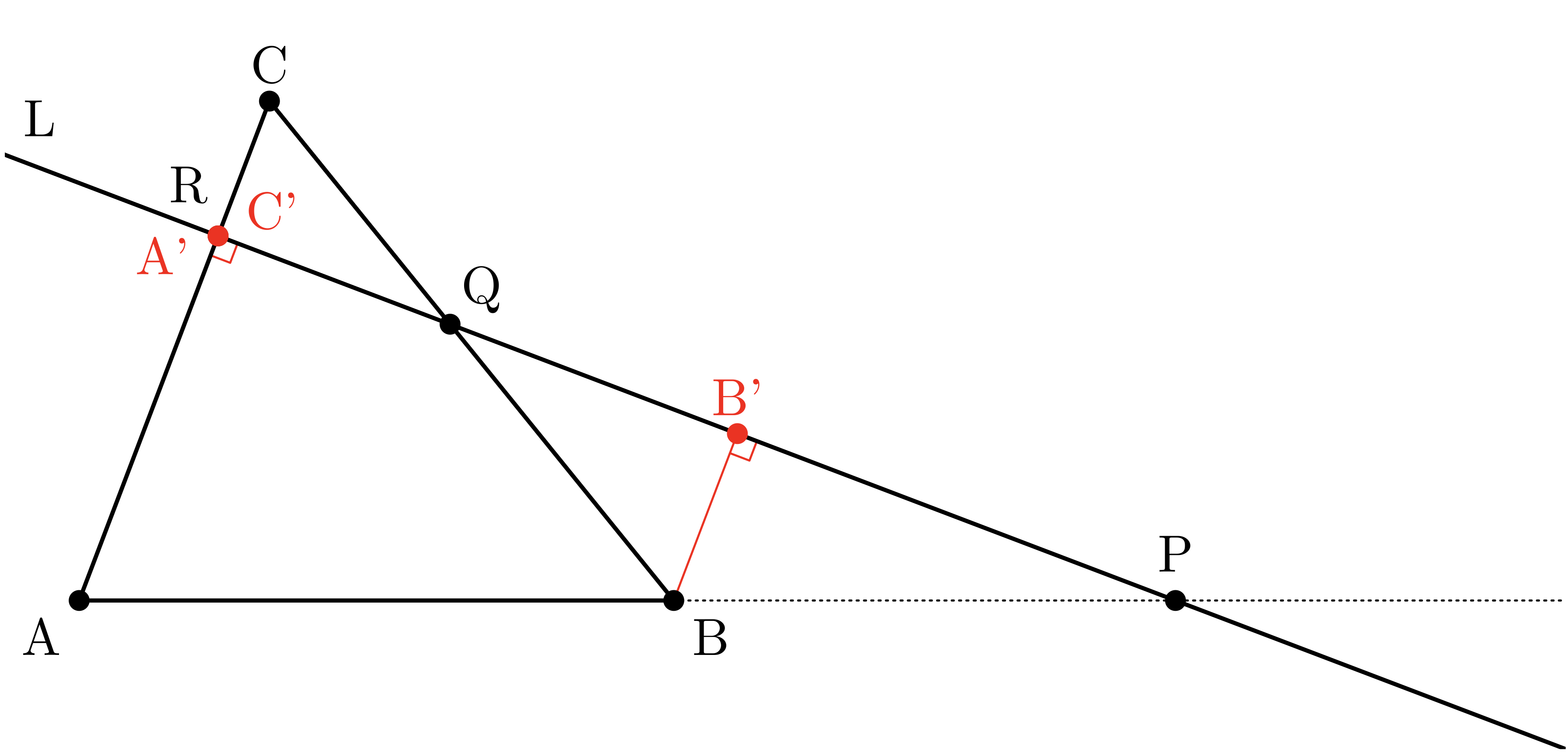
僕「うっ、それは痛いな……」
ユーリのダウトにより、僕はしばらく図をにらんだ。
ユーリ「そろそろ、ユーリの補助線を見せたげようかにゃ?」
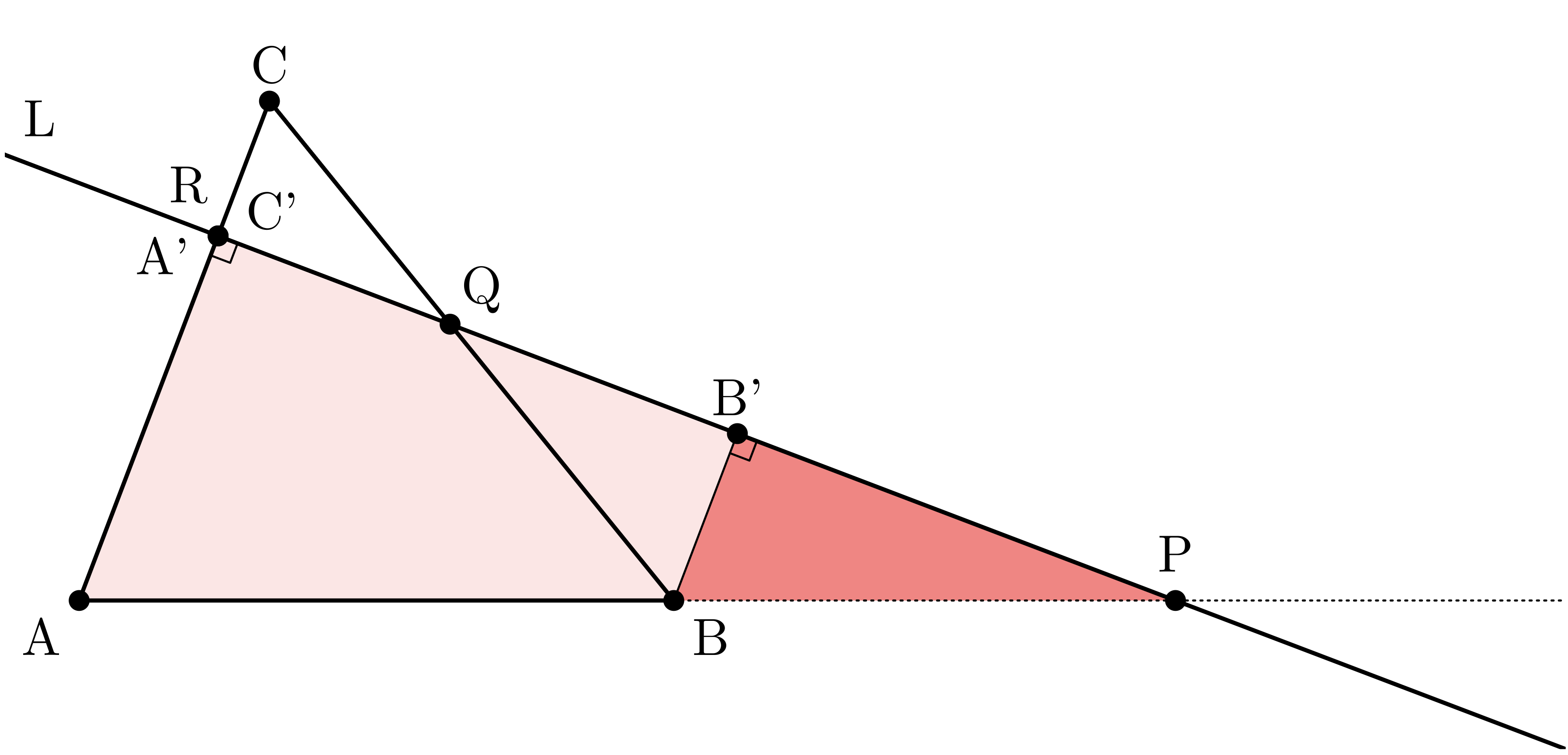
僕「いや、 辺 $\TT{CA}$ と直線 $L$ が垂直でも大丈夫だよ、ユーリ」
ユーリ「なんで? 三角形がつぶれちゃうのに?」
僕「辺 $\TT{CA}$ と直線 $L$ が垂直なときは、 三角形 $\TT{ARA'}$ や三角形 $\TT{CRC'}$ を作る必要はないんだ。 点 $\TT{R}$ に対して $\TT{A'}$ と $\TT{C'}$ と名前をつけるだけで自動的に $$ \frac{\TT{CR}}{\TT{AR}} = \frac{\TT{C'C}}{\TT{A'A}} $$ が成り立つ」
ユーリ「何言ってるかわかんない」
僕「こういうことだよ。式の上ではまったく同じになる」
$\TRI{APA'}$ と $\TRI{BPB'}$ は相似
$$ \frac{\TT{AP}}{\TT{BP}} = \frac{\TT{A'A}}{\TT{B'B}} $$
$\TRI{BQB'}$ と $\TRI{CQC'}$ は相似
$$ \frac{\TT{BQ}}{\TT{CQ}} = \frac{\TT{B'B}}{\TT{C'C}} $$
点 $\TT{R}$ に対して $\TT{A'}$ と $\TT{C'}$ と名前をつけた
$$ \frac{\TT{CR}}{\TT{AR}} = \frac{\TT{C'C}}{\TT{A'A}} $$
ユーリ「つぶれても、うまくいくんだ」
僕「うーん、でもユーリのダウトは的確だよ。 僕は考えが足りなかった。 きちんと証明を書くなら場合分けが必要になってしまう」
ユーリ「ふふん」
僕「ユーリはどんな補助線を引いたの? やっぱり相似を使うんじゃない?」
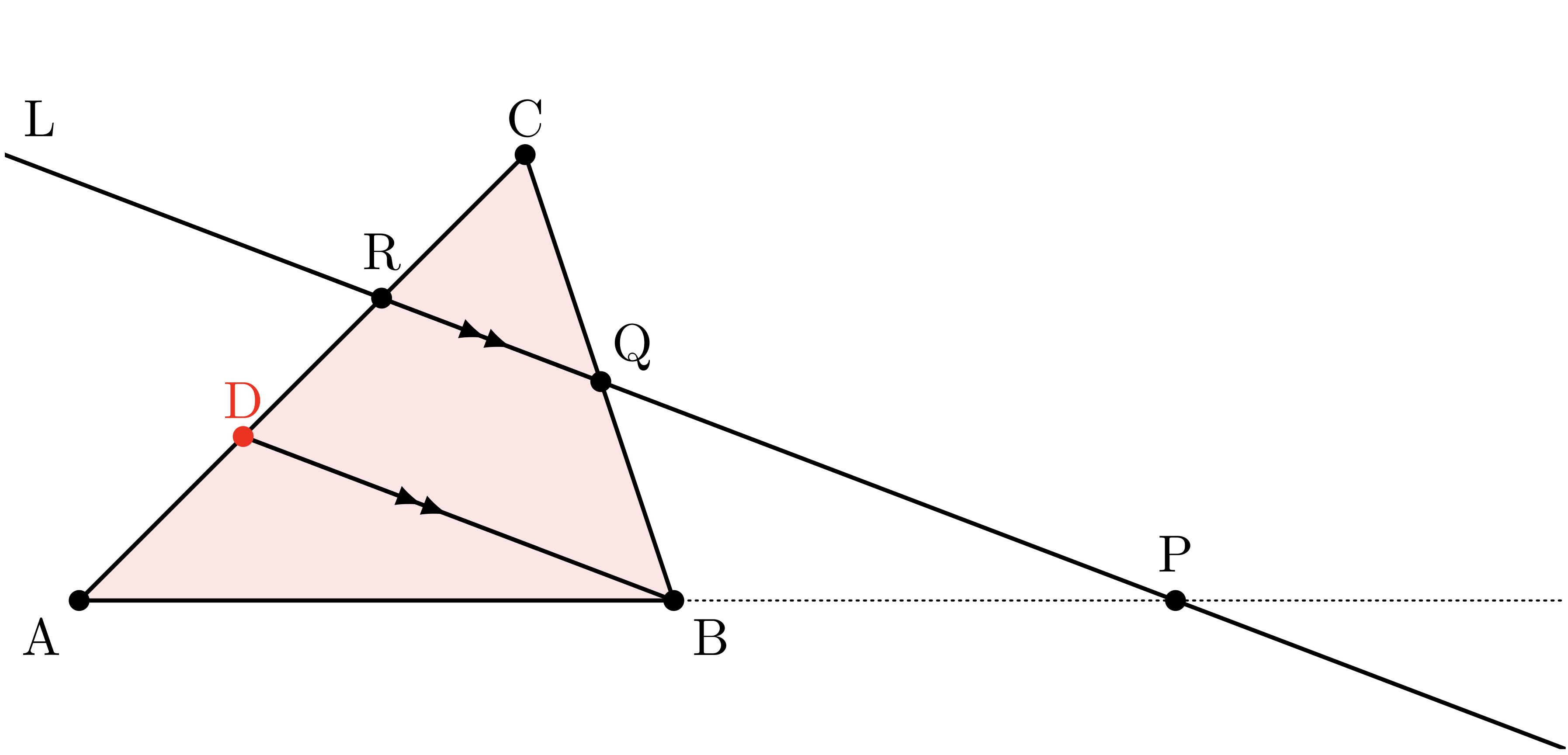
ユーリ「そだね。相似を使う。 直線 $\TT{L}$ と平行で、点 $\TT{B}$ を通る直線を引いて、 辺 $\TT{CA}$ との交点を $\TT{D}$ とすると……」
ユーリが描いた補助線
僕「なるほど……この補助線だと、相似な三角形を二組作れるね」
$\TRI{APR}$ と $\TRI{ABD}$ は相似
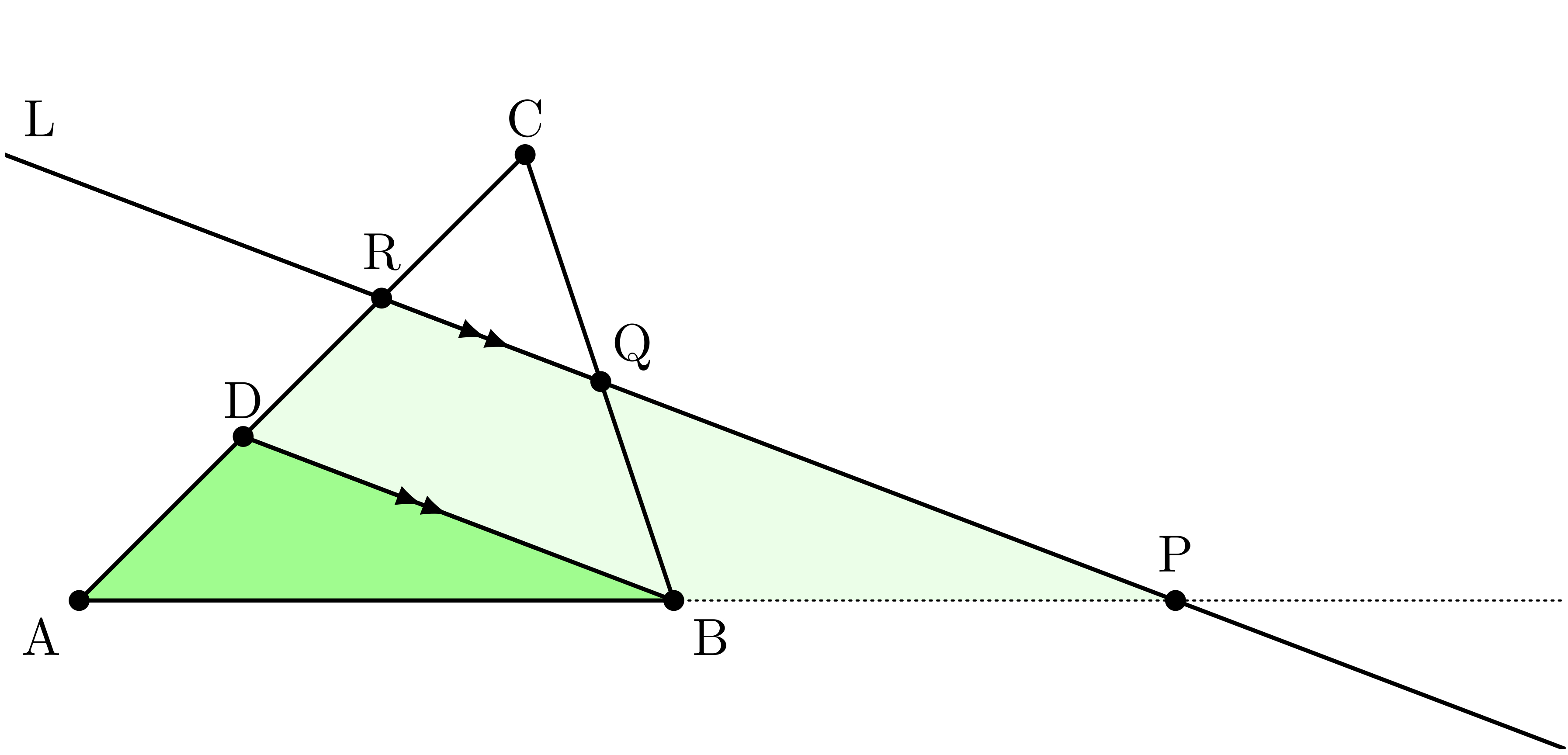
$$ \frac{\TT{AP}}{\TT{PB}} = \frac{\TT{AR}}{\TT{RD}} $$
$\TRI{CRQ}$ と $\TRI{CDB}$ は相似
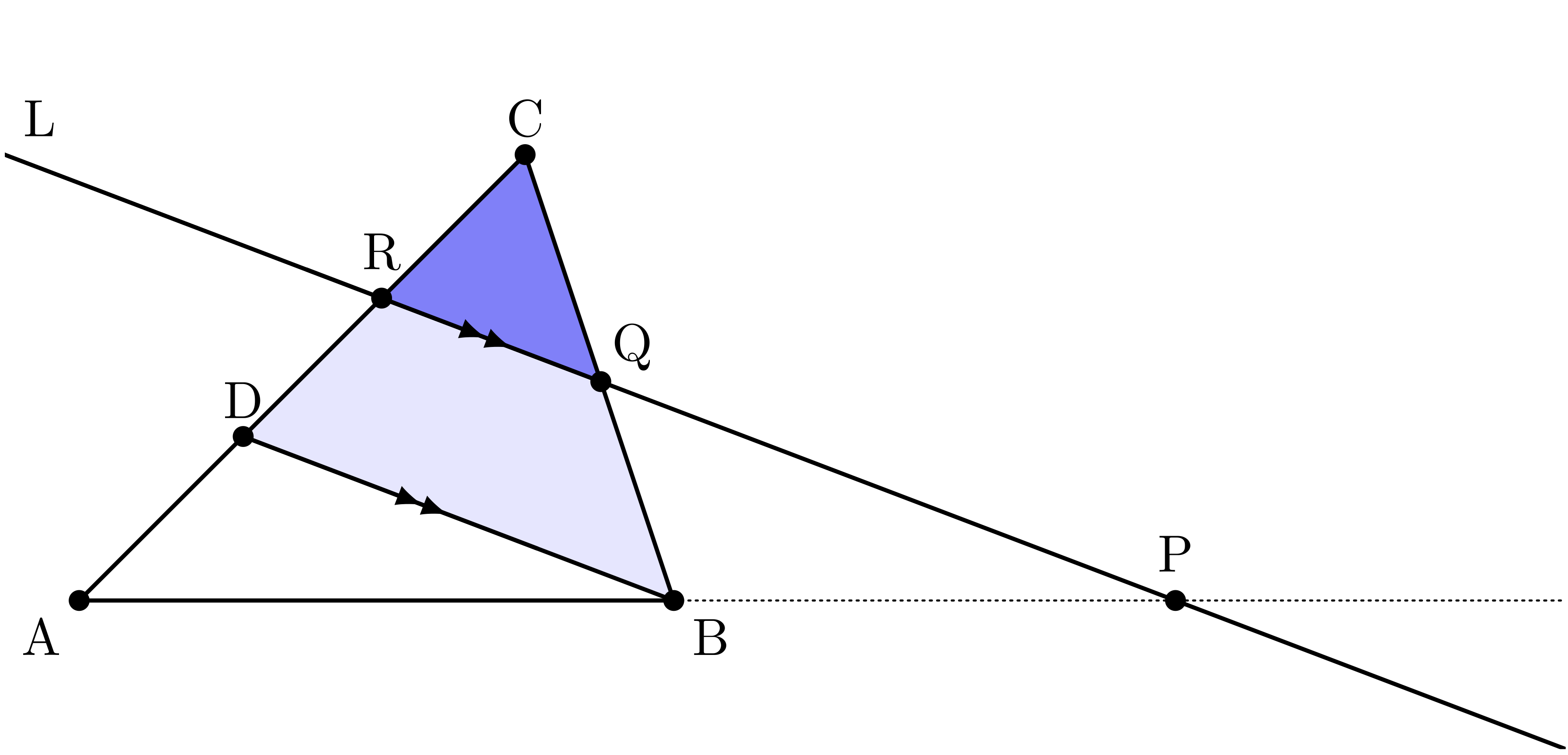
$$ \frac{\TT{BQ}}{\TT{QC}} = \frac{\TT{DR}}{\TT{RC}} $$
ユーリ「ねねね、ユーリの方が簡単でしょ?」
僕「そうだね。これはうまい補助線だね」
ユーリ「うまく見つけられれば、うまい補助線になる」
そこで僕は、あることに気付いた。
僕「ねえユーリ。気付いたことがある」
ユーリ「なになに? もっとうまい補助線? もっと簡単になる?」
僕「いや、たぶん簡単にはならない」
ユーリ「だったら意味ないじゃん!」
僕「簡単じゃない。でも、 補助線がたとえ見つけられなくても構わない。 補助線を使わなくても、メネラウスの定理は証明できる……と思う」
ユーリ「『と思う』なんだ」
僕「最後まで見通しているわけじゃないからだよ。 どうすればいいかというと……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第431回終わり)
(2024年9月13日)