第427回 シーズン43 エピソード7

多項式の謎、剰余の魅力（前編）

早くも第3刷になりました！

結城浩『群論への第一歩』はこちらです！

登場人物紹介

僕：数学が好きな高校生。

テトラちゃん：僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。

ここは高校の図書室。いまは放課後。

僕が計算をしていると、 後輩のテトラちゃんがやってきた。

いつものように、とても元気に。

数学の村木先生は、 僕たちにときどき《カード》を渡してくれる。

謎めいた数式がぽつんと書かれているときもあれば、 パズルが書かれているときもある。

ときに思わせぶりなその《カード》をきっかけに、 僕たちは自由に問題を作り、それを解いて楽しむのだ。

僕の軽口に、テトラちゃんも笑顔になって軽口で答えた。

新しい《カード》が来たので、 二人ともちょっと（・・・・）ウキウキ（・・・・）しているのだ。

さて、どんな問題なんだろう。

問題

$n$ は、 $2$ 以上の整数とする。

$x^n$ を $x^2 - x - 1$ で割った余りを $ax + b$ としたとき、

$a$ と $b$ は正の整数で、互いに素であることを証明せよ。

（2002年東京大学入試問題をもとにしています）

僕はテトラちゃんから渡された《カード》の問題をじっと見る。

パッと見た感じはそれほど難しそうには見えない。

もちろん、証明がすぐにわかるわけではないけれど、 手も足も出ないという感じではなさそうだ。

ともかく、方針ははっきりしている。

テトラちゃんはそう言ってコクコク頷いた。

こんなふうにして、僕たちはそれぞれに《カード》の問題に取り組むことにした。

もしここに、いとこのユーリがいたとしたら、

ユーリ「このときはまだ、心底おどろくことが起きるなんて、まったく思っていなかったのだ（ジャジャーン！）」

とか言いそうだな……と、僕は思った。

ちょっとじゃないな。僕は、すごく（・・・）ウキウキ（・・・・）している。

さて……と僕は考える。

$n$ は $2$ 以上の整数だから、 $$ n = 2,3,4,5,\ldots $$ ということ。そして $x^n$ を考えるのだから、 $$ x^2, x^3, x^4, x^5, \ldots $$ を考えることになる。

そして、どの場合であっても、 $x^n$ を $x^2 - x - 1$ で割った余りを $ax + b$ としたとき、

　 $a$ と $b$ が正の整数で、互いに素になる

ことが成り立つと示せばいい。

要するに

• $x^2$ を $x^2 - x - 1$ で割った余りについて、成り立つ。
• $x^3$ を $x^2 - x - 1$ で割った余りについて、成り立つ。
• $x^4$ を $x^2 - x - 1$ で割った余りについて、成り立つ。
• $x^5$ を $x^2 - x - 1$ で割った余りについて、成り立つ。
• ……

しかし、 $n = 2$ の場合、 $n= 3$ の場合、 $n = 4$ の場合、 $n = 5$ の場合……と、ひとつずつ証明していってもキリがない。

$2$ 以上の整数は無数に存在するからだ。

だから、もちろん、数学的帰納法を使って証明することになる——というのが僕の方針だ。

ここまでは一瞬で思いつく。

そして次は、

• $n = 2$ で成り立つ……（１）
• $n = k$ で成り立つならば、 $n = k+1$ で成り立つ……（２）

なぜなら、それがまさに数学的帰納法に他ならないからだ。

僕は、数学的帰納法のステップ（１）を考える。

$n = 2$ の場合だ。

これは、問題に書かれていることを具体的に式で表せばいいだけだ。

$x^2$ を $x^2 - x - 1$ で割った余りを $ax + b$ としたとき、 $a$ と $b$ が正の整数で、互いに素になる。

割り算を実行して余りを求めよう。

このくらいなら暗算でもできるけれど、まあ一応、書いてみるか。

$x^2$ を $x^2 - x - 1$ で割った余りは $x + 1$ になる

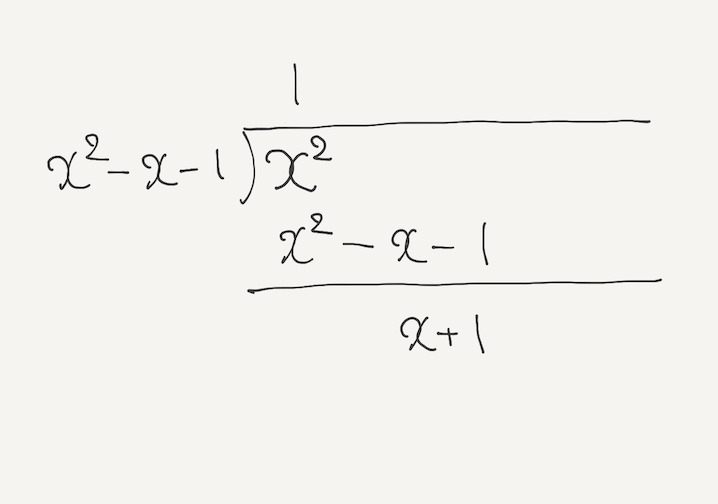
ということで、 $x^2$ を $x^2 - x - 1$ で割った余りは $x + 1$ になった。 つまり、 $$ ax + b = x + 1 $$ となるので、 $$ \begin{cases} a &= 1 \\ b &= 1 \end{cases} $$ になる。

待てよ。

$a$ と $b$ は $n$ に依存するわけだから、 $a$ も $b$ も数列として考えた方がよさそうだぞ。

$x^n$ を $x^2 - x + 1$ で割った余りは、 $a_nx + b_n$ として考えることにしよう。 すると、 $$ \begin{cases} a_2 &= 1 \\ b_2 &= 1 \end{cases} $$ になった。

そして、 $a_2$ と $b_2$ は正の整数で、互いに素であることがいえる。

$a_2 = 1$ と $b_2 = 1$ の最大公約数は $1$ だからだ。

これでステップ（１）はいえた。次は、ステップ（２）だ。

数学的帰納法のステップ（２）では、 $n = k$ で成り立つならば、 $n = k+1$ で成り立つことをいう。

ここで使えるのは《$n = k$ のときに成り立つ》ということだ。具体的にいえば、

　 $a_k$ と $b_k$ は正の整数で、互いに素である。

という命題がステップ（２）の前提となる。そして示すべきことは、

　 $a_{k+1}$ と $b_{k+1}$ は正の整数で、互いに素である。

という命題だ。 $k$ から $k+1$ に進めればOKだ。

やるべきことは明白。

$n = k+1$ のときに割り算を実行する。

つまり、 $x^{k+1}$ を $x^2 - x - 1$ で割ることになる。

割ったときの商がどうなるかはわからないから、具体的には書けない。 だから商を $Q_{k+1}(x)$ と呼ぶことにしよう。

そうすると、

• $x^{k+1}$ を $x^2 - x - 1$ で割ったとき、
• 商が $Q_{k+1}(x)$ であり、
• 余りが $\REDFOCUS{a_{k+1}x + b_{k+1}}$ である

$$ x^{k+1} = (x^2 - x - 1)Q_{k+1}(x) + \REDFOCUS{a_{k+1}x + b_{k+1}}\DOTNAME{\heartsuit} $$

これはただ多項式の割り算を書いただけだ。

やりたいのは $a_{k+1}$ と $b_{k+1}$ を調べること。

そのために使えるのは $a_k$ と $b_k$ の性質なんだから、 当然、 $$ x^k = (x^2 - x - 1)Q_k(x) + \BLUEFOCUS{a_kx + b_k}\DOTNAME{\clubsuit} $$ を使うことになる。

さあ、ここが考えどころだ。

$x^k$ を使って $x^{k+1}$ の謎を解くんだ……

$x^{k+1}$ を作るため、 $\clubsuit$ の両辺に $x$ を掛けてみようか。

$$ \begin{align*} x^k &= (x^2 - x - 1)Q_k(x) + \BLUEFOCUS{a_kx + b_k}\DOTNAME{\clubsuit} \\ & \downarrow\textrm{両辺に$x$を掛ける} \\ x^{k+1} &= x(x^2 - x - 1)Q_k(x) + \BLUEFOCUS{a_kx^2 + b_kx} \DOTNAME{\diamondsuit} \end{align*} $$

僕は、 $\heartsuit$ と $\diamondsuit$ を見比べる。

わかった！

こんな二式ができた。 $a_k,b_k$ を使って $a_{k+1},b_{k+1}$ を調べたい。

$$ \begin{cases} x^{k+1} &= (x^2 - x - 1)Q_{k+1}(x) + \REDFOCUS{a_{k+1}x + b_{k+1}} & \DOTNAME{\heartsuit} \\ x^{k+1} &= x(x^2 - x - 1)Q_k(x) + \BLUEFOCUS{a_kx^2 + b_kx} & \DOTNAME{\diamondsuit} \end{cases} $$

この二式の左辺は等しいから、右辺も等しい。

$\heartsuit$ は、多項式の割り算の形になっている。なぜなら、 $$ \REDFOCUS{a_{k+1}x + b_{k+1}} $$ は $x$ の $1$ 次式で、 $2$ 次式 $x^2 - x - 1$ よりも低い次数になっているから。

でも、 $\diamondsuit$ は違う！ 多項式の割り算の形になっていない。なぜなら、 $$ \BLUEFOCUS{a_{k}x^2 + b_{k}x} $$ は $x$ の $2$ 次式だ。 だからこれは、 $x^2 - x - 1$ で割ったときの余りじゃない。 もっと次数は下がる。

なるほどね。 だったら、

　 $\BLUEFOCUS{a_{k}x^2 + b_{k}x}$ を $x^2 - x - 1$ で割ってみよう。

そうすれば、

　 $x^{k+1}$ を $x^2 - x - 1$ で割ったときの余りを $a_k,b_k$ で表せる

はずだ。

よしっ、割り算実行！

$a_{k}x^2 + b_{k}x$ を $x^2 - x - 1$ で割った余りは $(a_k+b_k)x + a_k$ になる

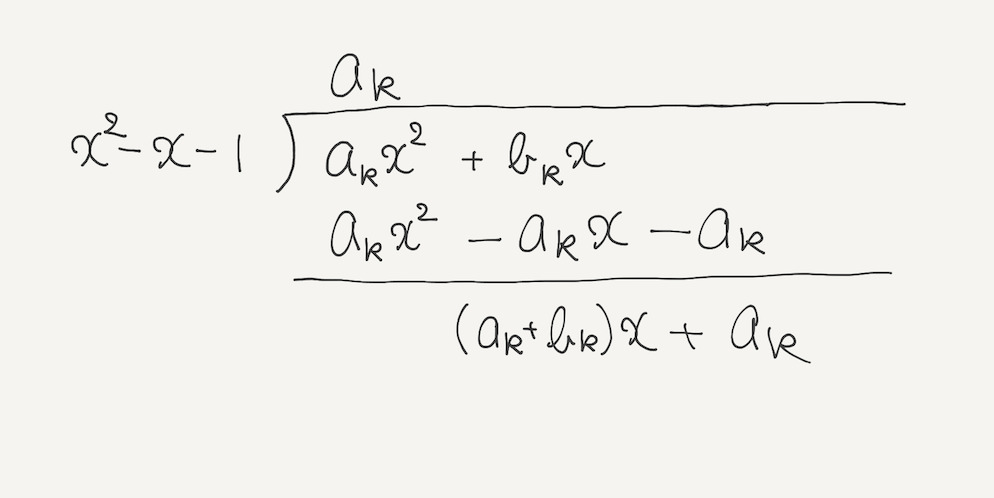
いまの割り算で、 $$ \BLUEFOCUS{a_{k}x^2 + b_{k}x} = a_k(x^2 - x - 1) + \GREENFOCUS{(a_k+b_k)x + a_k} $$ がわかった。 ということは、 $\diamondsuit$ から、 $$ \begin{align*} & x^{k+1} \\ &= x(x^2 - x - 1)Q_{k}(x) + \BLUEFOCUS{a_kx^2 + b_kx} \DOTNAME{\diamondsuit} \\ &= x(x^2 - x - 1)Q_{k}(x) + a_k(x^2 - x - 1) + (a_k+b_k)x + a_k \\ &= (x^2 - x - 1)(xQ_{k}(x) + a_k) + \GREENFOCUS{(a_k + b_k)x + a_k} \end{align*} $$ となった。最後の式を改めて $\spadesuit$ と名付けると、 $$ x^{k+1} = (x^2 - x - 1)(xQ_{k}(x) + a_k) + \GREENFOCUS{(a_k + b_k)x + a_k} \DOTNAME{\spadesuit} $$ となる。

ああ、もうゴールは見えたな。

こんな二式ができた。 $a_k,b_k$ を使って $a_{k+1},b_{k+1}$ を調べたい。

$$ \begin{cases} x^{k+1} &= (x^2 - x - 1)Q_{k+1}(x) + \REDFOCUS{a_{k+1}x + b_{k+1}}\DOTNAME{\heartsuit} \\ x^{k+1} &= (x^2 - x - 1)(xQ_{k}(x) + a_k) + \GREENFOCUS{(a_k + b_k)x + a_k}\DOTNAME{\spadesuit} \end{cases} $$

この二式の左辺は等しいから、右辺も等しい。

そしてどちらの右辺も $x^{k+1}$ を $x^2 - x - 1$ で割った形になっている。 余りは一意に定まるから、

$$ \REDFOCUS{a_{k+1}x + b_{k+1}} = \GREENFOCUS{(a_k + b_k)x + a_k} $$

となる。ここから、 $x$ の係数と定数項を比較して、 $$ \begin{cases} a_{k+1} &= a_k + b_k \\ b_{k+1} &= a_k \end{cases} $$ ができた。

あとは簡単だ。

ステップ（２）の前提から、

　 $a_k$ と $b_k$ は正の整数で、互いに素である。

が使える。そして、 $$ \begin{cases} a_{k+1} &= a_k + b_k \\ b_{k+1} &= a_k \end{cases} $$ を使えば、まず——

　 $a_k$ と $b_k$ は正の整数だから、 $a_{k+1}$ と $b_{k+1}$ はどちらも正の整数になる。

——はすぐにいえる。

そして——

　 $a_k$ と $b_k$ は互いに素だから、 $a_{k+1}$ と $b_{k+1}$ は互いに素になる。

——といえるか？　うん、いえるね！

こんなふうにすればいえる。

まず、 $a_{k+1}$ と $b_{k+1}$ の最大公約数を $g$ としよう。ここから $g = 1$ を導けばいい。 $g$ は最大公約数だから、 $$ \begin{cases} a_{k+1} &= gA \\ b_{k+1} &= gB \end{cases} $$ という整数 $A,B$ が存在して、 $A$ と $B$ は互いに素だ。 左辺を $a_k$ と $b_k$ で表すと、 $$ \begin{cases} a_k + b_k &= gA \\ a_k &= gB \end{cases} $$ となる。すると、 $$ b_k = (a_k + b_k) - a_k = g(A - B) $$ になる。

$a_k = gB$ で、 $b_k = g(A - B)$ だから、 $a_k$ と $b_k$ は $g$ という公約数を持つ。 ところが、ステップ（２）の前提から $a_k$ と $b_k$ は互いに素だから、 $g = 1$ だ。

したがって、 $a_{k+1}$ と $b_{k+1}$ の最大公約数 $g$ は $1$ となり、 $a_{k+1}$ と $b_{k+1}$ は互いに素になる。

これで、ステップ（２）も完成。

あとは証明を書き下ろすだけだ！

テトラちゃんがおずおずと声を掛けてきた。

僕は、はっと顔を上げた。

夢中になって考え、計算をしていたから、まわりがまったく見えてなかった。

そうだ、そうだ。

いまは放課後。ここは図書室。

目の前にいるのは大きな目がチャームポイントの後輩、テトラちゃんだ。