第426回 シーズン43 エピソード6

二乗したとき起きること（後編）

図書室にて

テトラ「ようやくできましたっ！　……ところで先輩も、こういう計算をユーリちゃんにしてみせたんですか？」

僕「うーん……そういうわけじゃない。僕は、ぜんぜん違う計算をしてた」

テトラ「ぜんぜん違う計算……とは？」

僕「いや、《ぜんぜん違う》は言いすぎかな。 最初はテトラちゃんと同じように $A = u + vi$ として $A = z^2$ を考え始めたんだけど、 入り組んだ計算になりかけたところで方針変更したんだ。 だから、いまテトラちゃんの計算を見ながら『ああ、根気よく進めばちゃんとたどり着くんだ……』と思ってたところ。 ありがとう、テトラちゃん」

テトラ「いえいえ。でも、方針変更——そうはいっても、 与えられた複素数 $A$ に対して $A = z^2$ となる複素数 $z$ を作るという方針は 変わらないんですよね？　だとしたら、 $$ z = a + bi $$ として $z^2$ を計算するしかないですよね？」

僕「そうでもないよ。僕は、 $$ z = r(\cos\theta + i\sin\theta) $$ として $z^2$ を計算したんだ」

テトラ「三角関数？！」

僕「そうだね。 でも、この表し方はテトラちゃんも知ってるんじゃなかった？」

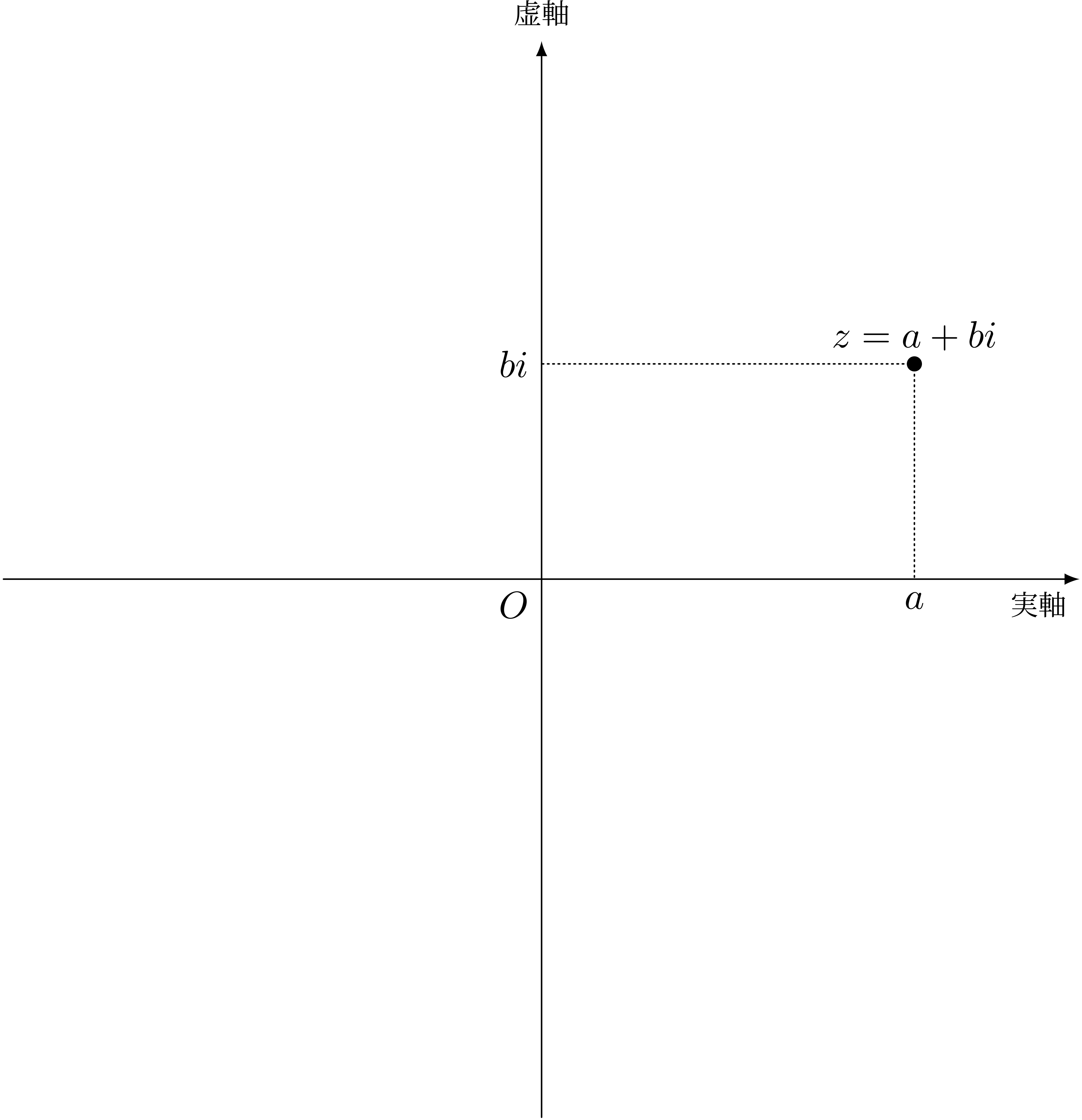
テトラ「は、はい……でも、あたしはそういうふうには頭が回りませんでした。 『複素数について一般的に考える』となると、 $$ z = a + bi $$ のようにして、複素数 $z$ を二つの実数 $a,b$ と虚数単位 $i$ を使って表す——と考えてしまいます」

僕「いや、もちろんそれは間違っていないし、悪いことでもないよ、テトラちゃん。 というか、とても素直で正しい方向だと思う。

• $z = a + bi$ は、直交座標（ちょっこうざひょう）で複素数を考えていて、
• $z = r(\cos\theta + i\sin\theta)$ は、極座標（きょくざひょう）で複素数を考えている

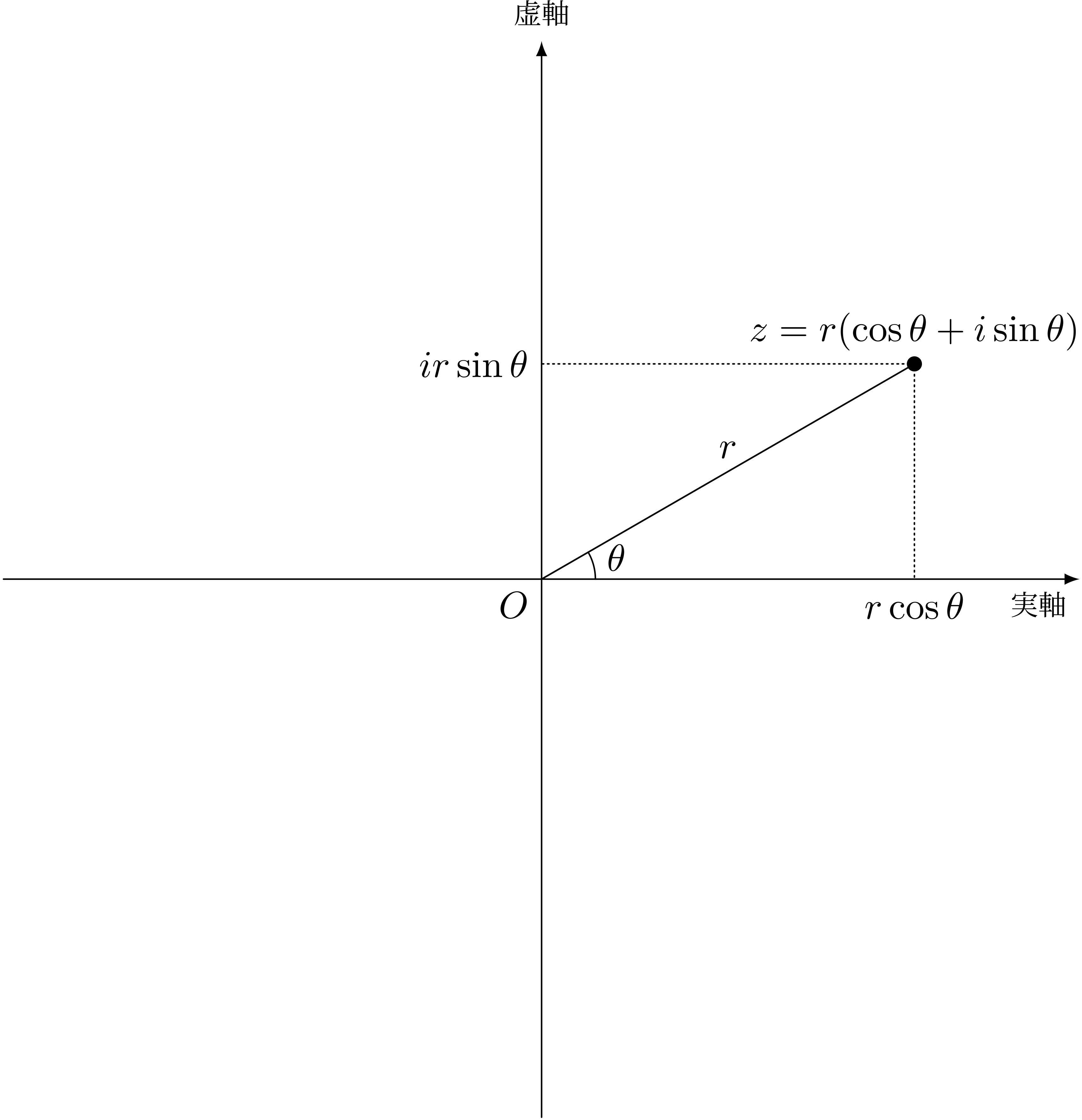
テトラ「なるほど。確かにそうですね」

僕「そしてテトラちゃんは、 直交座標で $z = a + bi$ と $A = u + vi$ のように複素数を考えたことによって、

　　《$A$ が与えられて $z$ を求める問題》

を

　　《$u,v$ を使って $a,b$ を表す問題》

に変換したといえるね。要するに《連立方程式を解く問題》形に変換したんだ（第425回参照）」

テトラ「確かに先輩のおっしゃる通りです。その変換で『これ、あたしにも解ける！』と思えました」

僕「だよね。問題を、自分の解ける形に変換するのはすごく大切だと思うな」

テトラ「自分のバトルフィールドに持ち込むわけですねっ！　アウェイじゃなくてホームで戦うっ！」

僕「まあ……そういうことになるのかな。もっとも、計算は大変だったけど」

テトラ「根気勝負ですっ！　……あ、すみません。それで、極座標だと、計算はどうなるんでしょう？」

僕「極座標でもやることは同じだよ。 $z^2$ の計算をするんだ。 複素数 $z$ を、 $$ z = r(\cos\theta + i\sin\theta) $$ で表して $z^2$ を計算すると、 $$ \begin{align*} z^2 &= \PS{r(\cos\theta + i\sin\theta)}^2 && \REMTEXT{$z$の定義から} \\ &= r^2 (\cos\theta + i\sin\theta)^2 && \REMTEXT{$2$乗を分けて計算} \\ &= r^2 (\cos^2\theta + 2i\cos\theta\sin\theta + i^2\sin^2\theta) && \REMTEXT{$2$乗を展開} \\ &= r^2 (\cos^2\theta + 2i\cos\theta\sin\theta - \sin^2\theta) && \REMTEXT{$i^2 = -1$} \\ &= r^2 (\cos^2\theta - \sin^2\theta + 2i\cos\theta\sin\theta) && \REMTEXT{実部をまとめた} \\ &= r^2(\cos^2\theta - \sin^2\theta) + r^2(2\cos\theta\sin\theta)i && \REMTEXT{実部と虚部に分けた} \end{align*} $$ となる。すなわち、 $$ z^2 = r^2(\cos^2\theta - \sin^2\theta) + r^2(2\cos\theta\sin\theta)i $$ となって——」

テトラ「あっ！　先輩っ！　その先の流れ、わかりましたよ。テトラ、しゃべってもいいでしょうか？」

僕「もちろんいいよ。何か気付いたの？」

テトラ「あたしたちがいまやろうとしているのは、 複素数 $A$ から、 $z^2 = A$ を満たす $z$ を求めることです。 いま先輩は $z^2$ を計算してますよね。 このあとに続くのは、 $A$ の方を $$ A = u + vi $$ とおいて、

　　《$z^2$ の実部が $u$ に等しくて、虚部が $v$ に等しい》

という条件を使うんじゃないでしょうか。 そして、それはすぐにできます。 だって、 先輩の計算から、実部と虚部をまとめると、 $$ z^2 = \underbrace{r^2(\cos^2\theta - \sin^2\theta)}_{\REMTEXT{実部}} + \underbrace{r^2(2\cos\theta\sin\theta)}_{\REMTEXT{虚部}} i $$ なりますからっ！　つまり、 $$ \begin{cases} u &= r^2(\cos^2\theta - \sin^2\theta) && \REMTEXT{実部} \\ v &= r^2(2\cos\theta\sin\theta) && \REMTEXT{虚部} \qquad\qquad\cdots\cdots\clubsuit \end{cases} $$ という連立方程式を解くことになるはずですっ！」

僕「うん、計算自体はおかしくないんだけど、それだとちょっぴりちぐはぐ（・・・・）だよ」

テトラ「ちぐはぐ……？」

僕「$z$ の方を極座標で考えて、 $A$ の方を直交座標で考えていることになるからね。 それはテトラちゃんのバトルフィールドとやらにこだわり過ぎていると思うな」

テトラ「ははあ……それではどうするんでしょう」

僕「$A = u + vi$ じゃなく、 $A$ の方も極座標で表示してみる。たとえば、 $$ A = R(\cos\phi + i\sin\phi) = \underbrace{R\cos\phi}_{\REMTEXT{実部}} + i\underbrace{R\sin\phi}_{\REMTEXT{虚部}} $$ とおいてみる。これで、 $R$ と $\phi$ （ファイ）を使って複素数 $A$ を表したことになる」

テトラ「あれ、でも、そこから結局 $$ A = z^2 $$ という式を書き換えて、 実部と虚部の連立方程式を作るんじゃないでしょうか。つまり、 この連立方程式のことです」

僕「そうだね」

テトラ「……」

僕「……」

テトラ「……あの、先輩？」

僕「うん」

テトラ「テトラの考え、聞いていただけますか？」

僕「もちろん。どうぞどうぞ」