![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕：数学が好きな高校生。
テトラちゃん：僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
リサ：自在にプログラミングを行う無口な高校生。コンピュータを自在に操る赤い髪の《プログラミング少女》。
僕とテトラちゃんはリサと共に最短経路問題に取り組んでいた（第416回参照）。
まずは最短距離を求めるアルゴリズム。 テトラちゃんの深さ優先探索ではうまく行かないことを理解して、 リサが書いてくれた幅優先探索アルゴリズムを読んだ（第417回参照）。
でも……それじゃ、最短経路はどうやって求めればいいんだ？
僕「リサが書いてくれた幅優先探索のアルゴリズムで、 $s$ から $g$ までの最短距離が得られるのはわかった」
テトラ「そうですね」
僕「その最短距離が得られる経路が最短経路になるわけだね」
テトラ「あれ……でも、その最短経路はどうやって得られるんでしょう」
僕「$\text{SHORTEST-PATH-LENGTH}$を少し改良すれば得られそうだけど……んんん？」
テトラ「つまり、こういう問題を解くことになります」
問題（最短経路問題）
グラフ $G$ と二頂点 $s,g$ が与えられているとき、 $s$から$g$までの最短経路を求めるアルゴリズム$\text{SHORTEST-PATH}$を考えてください。
入力
出力
グラフ $G$ の例（この場合の出力は $s \to x_1 \to x_2 \to g$）
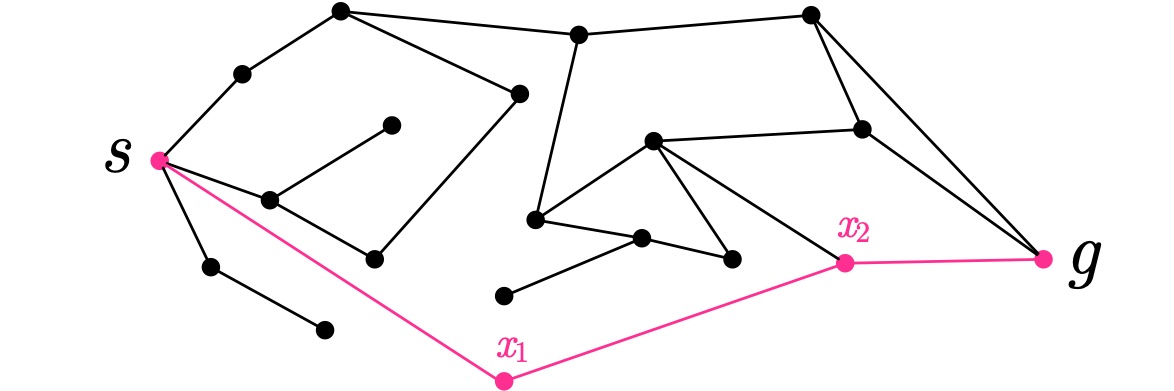
僕「そうだね。 だから、このグラフ $G$ の例でいうと、 $$ s \to x_1 \to x_2 \to g $$ という経路が出力になるんだね」
テトラ「そうですね……」
僕は考える。
最短距離については、 すでにリサが$\text{SHORTEST-PATH-LENGTH}$という形にアルゴリズムをまとめてくれた。
このアルゴリズムを使えば、最短距離がわかる。
ということは、まさにその最短距離を作り出している頂点もまたわかりそうだ。 そして最短距離を作り出している頂点がわかれば最短経路もわかったことになる。
つまり、この$\text{SHORTEST-PATH-LENGTH}$を改良する形で$\text{SHORTEST-PATH}$が作れそうだ。
僕「うん。ちょっと考えてみようかな……」
テトラ「あたしも考えます……」
僕は考える。
最短距離を求める処理では、 キュー $q$ から頂点 $u$ を一つずつ取り出して処理を行う（C9）。
$u$ に隣接している頂点 $v$ を順番に調べていくわけだが（C13からC18）、 $v$ はいわば《$u$ を中心とする単位円》上にある。
そのような $v$ のうちで未訪問なものをキュー $q$ に入れる（C16）。
だから……
僕「うん、わかったと思う。 C15で、 $$ v.\text{distance} \leftarrow u.\text{distance} + 1 $$ のように$v$の距離が決まる。ここで《波面》が進み、$v$を$\text{ENQUEUE}$している。 だから、この $v$ が最短経路上に現れることになるんじゃない？ つまり、 C15とC16のあいだで $v$ を出力すればいい——で、どうだろう」
テトラ「え？ 先輩、それは違うと思います」
テトラちゃんは顔を上げてきっぱりと言った。
おっと、反応が早いな。
僕「そう？」
テトラ「はい。C15で $v$ の距離が決まるのは確かです。 ええと、正確にいいますと、 $s$から$v$までの最短距離が$v.\text{distance}$に代入されたことになります」
僕「だよね？」
テトラ「確かに、その時点での $v$ に関してはそうです。 頂点 $v$ が最短経路上に現れる可能性は、確かにありますけれど、 まだ、ゴール $g$ までの最短距離はわかっていませんので……」
僕「可能性は、あるけれど——」
テトラ「はい、そうです。 頂点 $v$ が最短経路上に来る可能性はあります。 でも、最短経路上に来る保証はありませんよね？」
僕「うーん……そうなるか？」
テトラ「そうですよ！ だって、もしもC15とC16のあいだで頂点 $v$ が最短経路上に来るのだとするなら、 《波面》に乗って調べていく頂点のすべてが最短経路上にあることになってしまいますから！」
テトラちゃんは「すべて」と言いながら両腕を大きく広げた。
僕「あっ、それはそうか。 この幅優先探索アルゴリズムでは、 調べていく頂点をいったんキューに順序良く詰めておいて、 そこから取り出して調べるんだから——うわあ……僕の考えはぜんぜんダメじゃないか！」
ぜんぜん駄目だ。僕は、いったい何を考えてたんだ。
幅優先探索しているわけだから、《波面》上の頂点を順番に見ているに過ぎないんだ。 最短経路上にある保証なんて、どこにもない！
《波面》の進行と、C15で$v.\text{distance}$が決まっていく頂点の順番の例
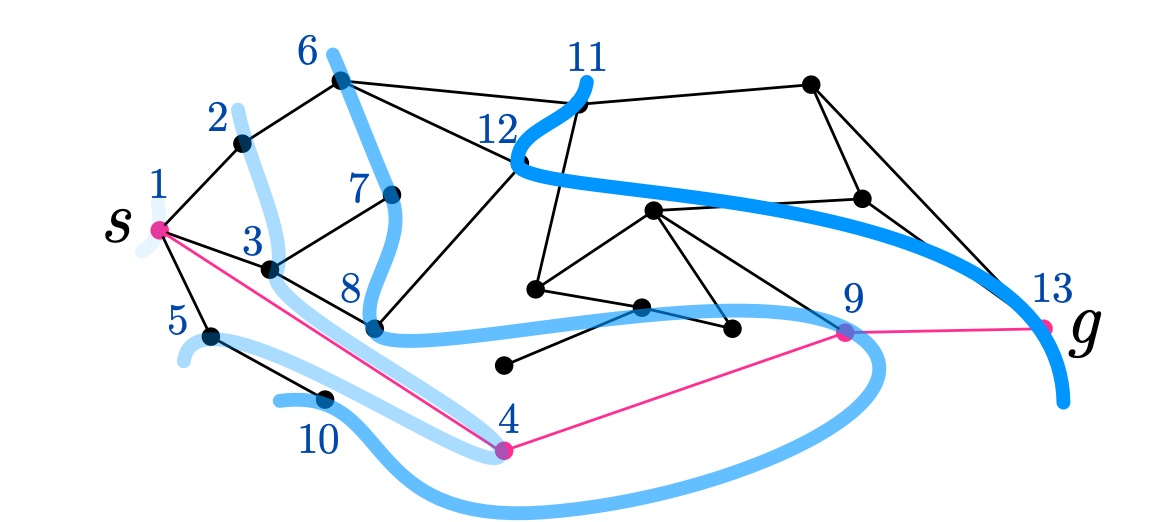
厳密にいえば、同一波面上での順序はC13の$\textbf{foreach}$で処理される頂点の順序に依存します。
テトラ「あ、あの……あたしの考えも聞いていただけますか？」
僕「テトラちゃんはもうできたの？」
テトラちゃんは 僕よりずっとプログラムやアルゴリズムに詳しい。 双倉図書館の一般講座に参加したこともあった（第321回参照）。
テトラ「い、いえ、できたんじゃなくて、 『こういうやり方ではうまく行かないはず』 ということがわかったんです」
僕「へえ……」
テトラ「あたしも先輩と同じように、 最短距離を求める $\text{SHORTEST-PATH-LENGTH}$を改良する方向で 最短経路を求める $\text{SHORTEST-PATH}$ を作ろうとしていました」
僕「うん。最短距離がわかるんだから、それを求めるときに使う頂点もわかりそうだよね」
テトラ「でも、あたし、気付いたんです。 いま調べている頂点が最短経路上にあるかどうかは、 最短経路を探索している途中では絶対にわからない——ということに！」
僕「途中では絶対にわからない……それは、ゴールにたどり着くまではわからないという意味？」
テトラ「ですです。 キューから頂点 $u$ を取り出して、 $u$ を中心として半径 $1$ の《円周》上にある頂点——つまり $u$ に隣接している頂点——を調べます。 ところで、頂点 $u$ が最短経路上にあるということは、 処理がC11に達したときに、ようやくわかるんです。 そしてそれは処理が終わる直前なんですよっ！」
僕「……」
テトラ「C11に来たときの頂点 $u$ は確かに最短経路上にあります。 でも、C11での頂点 $u$ というのは要するにゴール $g$ です。そりゃ、最短経路上にありますよね……」
テトラちゃんはそう言うと両手で頭を抱えた。
確かに僕も両手で頭を抱えたくなる気分だった。
僕「つまりテトラちゃんが言いたいのは、 『この頂点は最短経路上にある』 と判断しながら処理を進めていく方法はうまく行かないってこと？」
テトラ「はい。ですからあたしは先ほど、先輩の考えが即座に『おかしい』とわかったんです……あ、す、すみません」
僕「いやいや、謝る必要は何もないよ。 実際ダメダメだったからね……うーん、でも、 だとしたら、どうすればいいのかな。難しいぞ」
テトラ「これって、矛盾してませんか……」
リサ「情報を残しつつ、たどる（咳）」
さっきから無言でコンピュータのキーボードを打っていたリサが、 こちらも見ないでぽつりと言った。
僕「情報を残しつつ……たどる？」
テトラ「情報を残しつつ……たどる？」
僕とテトラちゃんはオウム返しにそう言うと、顔を見合わせた。
そして二人で同時に「どんな情報を？」と言った。
思考がシンクロしてる。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2024年3月1日）
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)