第417回 シーズン42 エピソード7

次の一歩はどっちかな？（前編）

図書室にて

僕「……テトラちゃんはすでにアルゴリズムをちゃんと清書していたんだね！」

テトラ「はい……でも、 でも、これじゃうまくいかないんです！」

僕「A2からA4では、初期化を行っているんだね。 つまり、グラフ $G$ のすべての頂点 $v$ について、 $$ v.\text{visited}\leftarrow\FALSE $$ とすることで未訪問であることを表した。 そしてA5ではスタートとなる頂点 $s$ に対して、 $$ s.\text{visited}\leftarrow\TRUE $$ とすることで訪問したことを表した。 これは間違っていないよね？」

テトラ「はい、少なくともその処理自体は間違っていません。 そして$\text{LENGTH-TETRA}$で再帰的に$s$から$g$までの最短距離を得ています……得ようとしていますが、 実際のところ、これでは最短距離は得られないんです……」

僕「ざっと見た感じではうまく行きそうなんだけどなあ……。 どこかにバグがあるってことだよね。 ええと——」

テトラ「……」

僕「うーん……アルゴリズムは難しいね。 具体的なグラフを見れば少し試すだけで最短距離はわかる。 たとえば、さっきのグラフの例だと最短距離は $3$ になる。 でも、アルゴリズムは、どんなグラフでも最短距離が得られるようにしなくちゃいけないんだよね」

テトラ「そうなんです。ところで先輩はあたしの$\text{LENGTH-TETRA}$をどのように読みましたか」

僕「どのように読んだか？　そりゃ、B1の行から順に読んでいったよ。 そして、おおよそこういう動きなんだなとつかんだけど、僕にはどこにバグがあるか、まだわからない」

B2からB4

テトラ「アルゴリズムは、 さらさらっと読むのではなく、 自分がコンピュータになった気持ちで読むのだそうです（『数学ガール／乱択アルゴリズム』参照）」

僕「それは僕も聞いたことがある。まだピンと来てないところはあるけど……順番に読んでいくとして、 たとえば、$\text{LENGTH-TETRA}$のB2からB4までは、 『もしも $s = g$ なら出力は $0$』ということだと思う」

テトラ「そうですね。プログラムの文面を文字通り読めばそうですし、 少し抽象度を高くすると『もしもスタートとゴールが一致しているなら、最短距離は $0$』と読むこともできます」

僕「なるほど。『$s = g$』よりも『スタートとゴールが一致』の方が具体的なのに『抽象度が高い』っておもしろいね」

テトラ「ああ、言われてみればそうですね！　なぜでしょう……たぶんですけれど、 機械に近い方が抽象度が低くて、意味や解釈が加わるほど抽象度が高いんでしょう」

B5からB15

僕「$\text{LENGTH-TETRA}$のB5からB15までは、 スタートの $s$ に隣接した頂点 $v$ 一つ一つに対して、 $v$ から $g$ までの最短距離を再帰的に調べていて……うん、 B12で $l + 1$ を出力しているのは『$v$ から $g$ までの最短距離 $l$ に、 $s$ から $v$ までの $1$ を加えている』 ってことだよね。 $l$ がどうして $v$ から $g$ までの最短距離かというと、 B8で $$ l\leftarrow\text{LENGTH-TETRA}(G,v,g) $$ と代入してるから。 ここで$\text{LENGTH-TETRA}$を再帰的に使っていることになる。 うん、だから何がバグってるかよくわからない」

テトラ「この$\text{LENGTH-TETRA}$では深さ優先探索になってしまうんです」

僕「深さ優先探索？」

テトラ「はい。先輩がおっしゃるように、 B5からB15までは $s$ に隣接した頂点 $v$ 一つ一つを調べていき、 $v$ から $g$ までの最短距離を再帰的に得るんですけれど、 再帰的に$\text{LENGTH-TETRA}$を呼び出すときの呼び出し方が重要になります」

僕「ははあ……そういえば、深さ優先探索の話も聞いたことがあったなあ（第296回参照）」

テトラ「$s$ に隣接した頂点 $v$ を一つ選んで（B5）、 もしもその頂点 $v$ が未訪問だったら（B6）、 まず訪問済みの印を付けます（B7）、 そして次です！　次にB8で$\text{LENGTH-TETRA}$を呼び出してしまいます。 つまり、 $v$ から先の経路を調べ始めてしまいます。より深い探索に入ってしまうんですね。 だからこのアルゴリズムは深さ優先探索になります」

僕「そうか！　深さ優先探索だと、見つかった距離が最短距離になっている保証がないんだね！」

テトラ「ですです。たとえば先ほどの例だと、 最短経路はこっちで距離は $3$ なんですが——」

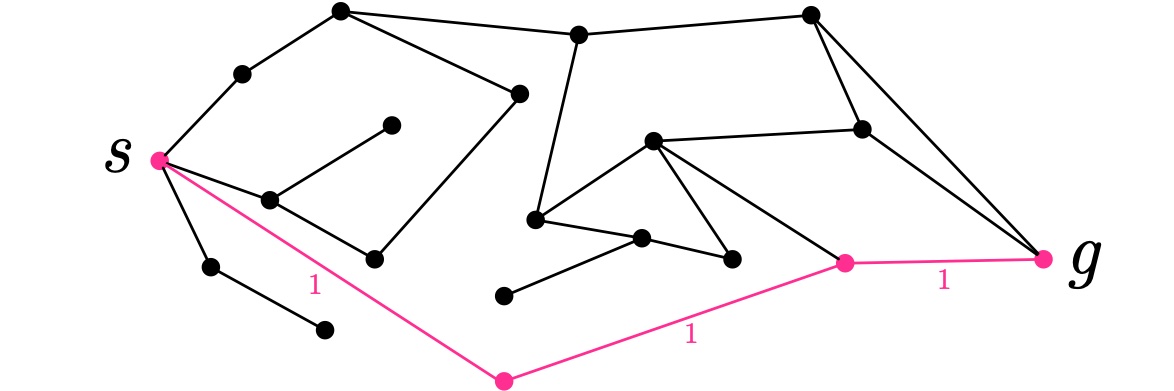
僕「……」

テトラ「深さ優先探索だと、 こういう経路が見つかってしまって $5$ を最短距離としてしまう間違いになるかもしれません」

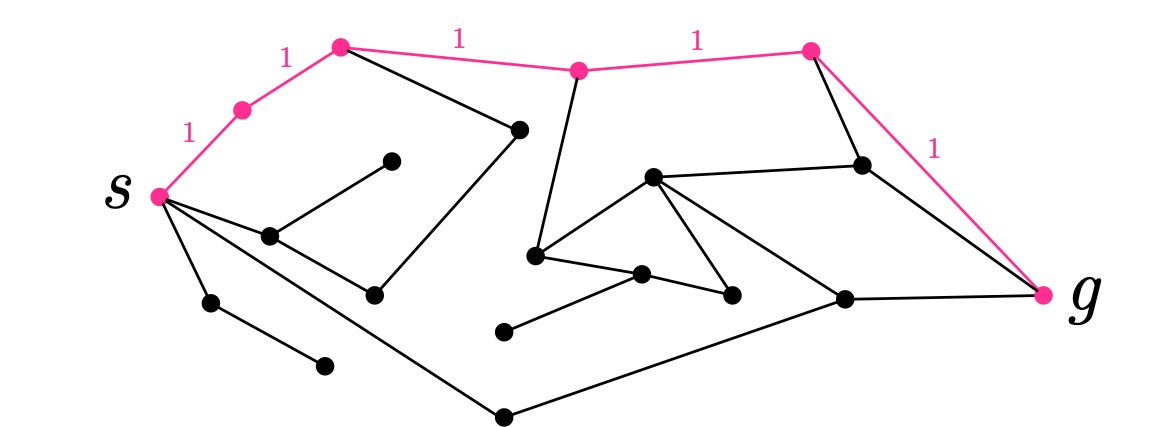
僕「確かにね……なるほど。 テトラちゃんがいう『B8で$\text{LENGTH-TETRA}$を呼び出してしまう』という感覚がわかったよ。 頂点 $v_1,v_2,v_3,v_4$ のどれが最短経路の一歩目になるか、まだわかってないうちから、 $v_1$ から先に深く $x$ へ進んで $g$ までの経路が最短だと決めつけて進むのは、そりゃまずいね。 最短経路を探すのに深さ優先探索はまずい……」

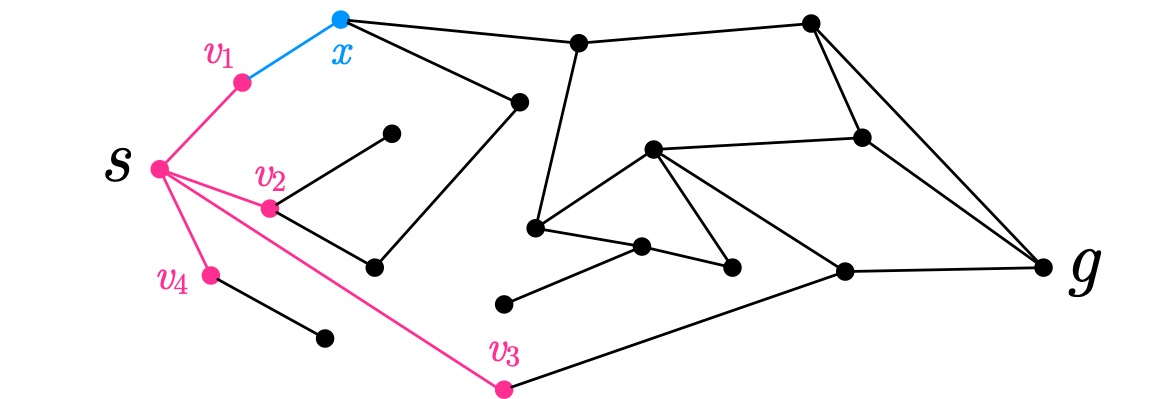
テトラ「もちろん、深さ優先探索をしてたまたま（・・・・）最短距離が見つかることもあります。 でもそれは偶然そうなっただけですし、 与えられたグラフ $G$ と、 $s$ に隣接した頂点集合から頂点を取り出す実装に依存する話です」

僕「実装に依存するというのは、どういうこと？」

テトラ「あっ、すみません。 動作するプログラムを実際に作る場合には、 $s$ に隣接した頂点集合の中から頂点をどのような順番で選んでくるかを決めなくてはいけません。 同じグラフ $G$ であっても、最短距離になるかどうかは、その選ぶ順番に依存してしまうという意味です」

僕「なるほど」

テトラ「あたしも深さ優先探索のアルゴリズムを最初に書いてしまったんです。 探索の方向性がまちがっていることはリサちゃ……リサに指摘されました」

僕「深さ優先探索じゃなくて——」

リサ「幅優先探索」

幅優先探索

僕「これが……幅優先探索で $s$ から $g$ までの最短距離を求めるアルゴリズムになるの？」

リサ「そう」