第419回 シーズン42 エピソード9

距離空間の定義（前編）

図書室にて

僕「数学の話？　僕も聞いていい？」

テトラ「あっ、先輩っ！　もちろんです。 いまミルカさんから、距離空間（きょりくうかん）についてのお話を聞いていたところです」

僕「あれ、そうなんだ。 僕はてっきりテトラちゃんがミルカさんに向かって《講義》してたんだと思ったよ」

テトラ「いえいえ、とんでもありません。逆です、逆です。 《講義》していたのはミルカさんの方です。 あたしは、いまちょうどミルカさんに質問してたところなんです」

僕「ずいぶんダイナミックな質問だね……距離空間？」

テトラ「はい、そうです。 先輩から《格子点の世界》のお話を聞いたり（第411回参照）、 リサちゃんから《最短経路の問題》を聞いたりしたじゃないですか（第416回参照）。 そこではいつも距離というものが鍵になっていました」

僕「うん、そうだね。世界を渡るパスポートのように」

テトラ「距離っていうと、こーんな感じですよね？」

僕「まあね」

テトラ「でも、そもそも距離って何？　……と考え始めて、ミルカさんに質問して、 それで、距離空間の話になりました」

僕「へえ……」

テトラ「でも、まだモヤモヤしているところがあってですね……」

ミルカ「ちょうどいい。いまからテトラは、彼に距離空間の《講義》をする」

テトラ「えっ、あ、あたしが話すんですか？」

ミルカ「そう」

ミルカ「テトラはすでに、距離空間の定義を知っている」

テトラ「あ、はい、一応……でもそれは、いまミルカさんからお聞きしたばかりからです。 まだ、きちんと理解していません」

ミルカ「だからこそ、テトラが話す。きちんと理解するために」

テトラ「……わかりました。先輩、あたしの距離空間の話、聞いていただけますか？」

僕「もちろん。最近は、テトラ先生に教えてもらってばかりだね」

距離空間

テトラ「えっと……では、思い出しながら順番にお話しします」

僕「はい、よろしくお願いします」

テトラ「距離の話をするんですが、距離だけを取り出して話をするのは難しいので、 距離空間の話をします。ええと、はい、距離空間の話の中に距離もいっしょに出てくるからです」

僕「うん」

テトラ「距離空間を定義していきますが、そこでまず、一つの集合と一つの関数を組にして考えます。 説明のために名前を付けますけれど、名前は本当のところは何でも構いません。 集合には $S$ と名前を付けて、関数には $d$ と名前を付けます。 その二つの組は、 $$ (S,d) $$ のように書くことにします。 そして、これから、集合 $S$ と関数 $d$ の組 $(S,d)$ が持っている——持つべき？ 四つの条件を説明します。 それで……ええと……その四つの条件が成り立っているとき、 この $(S,d)$ のことを距離空間ということにします」

僕「うんうん。いまテトラちゃんは、距離空間の定義を話そうとしているんだね。いいよ」

テトラ「最初の条件ですが——」

ミルカ「その前に、 $d$ がどんな関数か知りたい」

テトラ「あっ、そうですね。そうでした。いまは集合 $S$ と関数 $d$ の組 $(S,d)$ を考えようとしています。 集合 $S$ は——何かの集合です。 何かの集合って変ですね。距離を考える対象となるものの集合です。 集合の元（げん）、つまり集合の要素は点として考えると考えやすいです」

僕「うん、いいよ」

テトラ「それで、関数 $d$ は集合 $S$ の二つの要素のあいだの距離を表す関数になります。 $d$ という名前は、英語で距離を表すdistance（ディスタンス）の頭文字から取っています。 もちろん関数の名前は $f$ でもいいのですけれど、 $d$ としておくと『距離を表している』ということを思い出しやすくなります」

僕「そういえば、リサちゃんが作ってくれたプログラムでも、 フィールドの名前にdistanceが出てきたね（第417回参照）。 グラフ中の$v$という点の距離を$v.\textrm{distance}$で表していた」

テトラ「ですです。 $v.\textrm{distance}$は、スタートになる点$s$と$v$との間の距離でした。 距離を考えるというのは『二つの点の距離』を考えることですが、 スタート点 $s$ が決まっていたので、 $v.\textrm{distance}$は$v$という一つの点だけが表に出てきていたことになります」

僕「言われてみれば、確かにそうだね」

テトラ「いま定義しようとしている関数 $d$ は、関数ですから、 どの集合からどの集合への関数であるかをはっきりさせる必要があります……ありますよね？」

テトラ「リサちゃんと最短経路のアルゴリズムを考えていたときは、 二つの点の距離は $0,1,2,\ldots$ という $0$ 以上の整数でした。 でもいまは整数に限らずもっと一般的な距離を考えます」

僕「なるほど」

テトラ「距離を表す関数 $d$ は、 集合 $S\times S$ から実数全体の集合 $\REAL$ への関数 $$ d\colon S\times S \longrightarrow \REAL $$ として考えることにします……ですよね？」

ミルカ「テトラは理解している。確認せずに進んでいい」

テトラ「は、はい。 集合 $S\times S$ というのは、 $S$ の要素二つを並べてペアにしたもの全体の集合です。 二つの要素は等しくても構いません」

ミルカ「$S\times S$ は、 $$ S\times S = \SET{(x,y)\SETM x \in S, y \in S} $$ ということ。 $S$ と $S$ の直積集合（ちょくせきしゅうごう）という」

テトラ「そうでした。直積集合」

僕「なるほど、距離を測ろうとする二つの点を考えるために、 二つの点の組をすべて集めた集合が $S$ と $S$ の直積集合 $S\times S$ なんだね？」

テトラ「そうです、そうです。そして、二点 $x$ と $y$ の距離を、関数 $d$ の値として $$ d(x,y) $$ と表そうというのです」

僕「$x$ と $y$ はどちらも $S$ の要素で、 $x$ と $y$ のペアを与えると、 $x$ と $y$ の距離を表す実数を得る関数が $d$ になる——という理解でいいのかな？」

テトラ「はい、そうなります」

ミルカ「気持ちとしては『$d(x,y)$ は $x$ と $y$ の距離を表す』のだが、 距離と呼ぶ概念をいまから定義しようというのだから、 『距離を表す』と言い切ってしまうのはおかしいといえばおかしい。 まだこの段階では距離という概念は未知なのだから。 すべてを定義し終えた後になって初めて『$d(x,y)$ の値を距離と呼ぶ』という方がいいな」

テトラ「え……」

僕「関数 $d$ を使って距離という概念を定義するのであって、 僕たちが常識として知っている距離という概念で関数 $d$ が規定されるわけではない——ということ？」

ミルカ「そういうこと。 距離の概念を数学的に定義したいのだから、 私たちが日常的に知っている距離の概念は念頭に置きつつも、 定義に紛れ込ませないように注意が必要だ。 さもないと、数学の自由度が失われてしまう危険性がある」

僕「自由度？」

ミルカ「『《それ》は、常識的な感覚では距離とはいえないけれど、定義に従えばまちがいなく距離といえる』 という感覚のこと。日常的な感覚を土台にすえてしまうと、この自由度が失われてしまい、 数学が不自由になってしまう。定義の適用範囲が日常的な感覚から離れられなくなるから」

テトラ「わかりました！　いつもの《知らないふりゲーム》ですねっ！」

ミルカ「そう、それだ。便宜的に『距離』という言葉を使ったとしても、 いつでも《知らないふり》に戻れるようにしておく必要がある」

僕「距離というものはまだ知らない。 知っているのは、集合や関数や実数といった数学的対象だけということにするんだね」

（１）距離は $0$ 以上

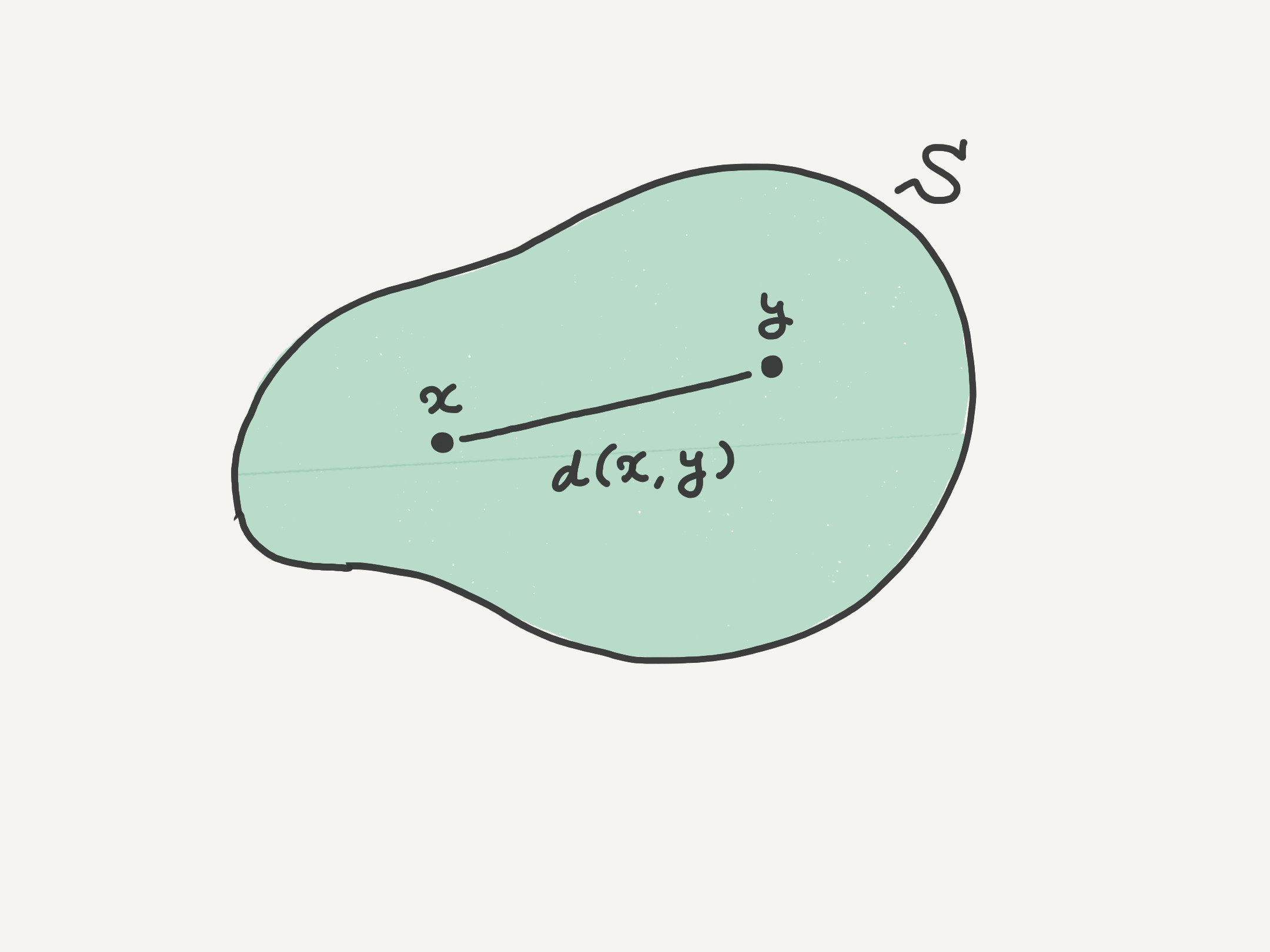
テトラ「あたしたちは、距離空間を定義しようとしています。 そして、先ほどの関数 $d$ に対して四つの条件を定めます。 条件を定めますというか……関数 $d$ は四つの条件を満たすものとします、の方がよさそうです。 関数 $d$ が具体的には何なのかはこっちに置いといて、 ともかく四つの条件は成り立っていることはわかっている——とするんです」

僕「条件が四つあるんだね」

テトラ「はい。その条件（１）は『関数 $d$ の値は必ず $0$ 以上になる』というものです」

僕「うん、それはわかるな。 $-1$ のような『負の距離』は考えないことにするんだ」

テトラ「そういうことです。お気持ちとしてはそうなります」

ミルカ「『関数 $d$ の値は必ず $0$ 以上になる』とテトラがいう、その《必ず》の意味は？」