![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
リサ:自在にプログラミングを行う無口な高校生。コンピュータを自在に操る赤い髪の《プログラミング少女》。
ある日の放課後。
僕がいつものように図書室に行くと、 後輩のテトラちゃんが、リサと並んで座っていた。
テトラちゃんは僕を見て声を上げる。
テトラ「先輩! ちょうどいいところに!」
僕「ちょうどいいところ?」
リサ「……」
リサは赤い髪をした女の子。
彼女はいつも真っ赤なノートブック・コンピュータのキーボードを叩いている。 ちなみにキートップには何の文字も書かれていない——無刻印、というやつだ。 彼女は、流れるようにコンピュータを操る《プログラミング少女》である。
いまも無言のまま、リサはキーボードを打ち続けている。 一瞬だけ僕を見たけど、特に表情は変わらない。
テトラ「先日《格子点の世界》のお話をうかがいましたよね」
テトラちゃんは、 僕が席に着くやいなや話し始める。
僕「うん、そうだった。 《格子点の世界》で何歩歩くかという《距離》を使って《円》や《楕円》や《双曲線》を描いたよね(第415回参照)。 また何か、新しい形を探り出したの?」
テトラ「いえ、《新しい形を探り出した》んじゃなくて——《形の新しい探り出し方》を考えていたんです。 いわば、探り出し方を探ってたんですねっ!」
僕「ええと……形の新しい探り出し方?」
テトラちゃんはいったい、何の話をしているんだろう。
そして、リサはいったい、何を書いているんだろう。
リサ「……」
テトラ「あたしが最初に考えていたのは《単位円》のことです」
僕「単位円。原点が中心で半径が $1$ の円」
座標平面上の単位円

テトラ「はい、そうです。 そして、その概念を《格子点の世界》に持っていきます。 原点から $1$ 歩だけ進んだところにある点全体の集合——つまり、それが、いわば《単位円》です……よね?」
僕「そうだね。原点から $1$ 歩だけ進んでたどり着ける点を、 原点からの《距離》が $1$ の点と見なすわけだから。 だから、 $$ \SET{(1,0),(0,1),(-1,0),(0,-1)} $$ という $4$ 個の点からなる集合は、《格子点の世界》の《単位円》と考えることができる。確かにその通り」
《格子点の世界》の《単位円》

テトラ「単位円は大切だなあ……とあたしはいつも思っています。 たとえば、三角関数を定義するときも単位円が出てきますし。 なのであたしは、この $4$ 個の点をじっと見ていました……」
僕「なるほど」
なるほど……と僕は思った。観察するテトラちゃんだ。
確かにテトラちゃんの言う通り、単位円は大切だ。 $\cos\theta$ も $\sin\theta$ も、ひいては $\tan\theta$ も単位円を使って定義できる。
それはきっと、それがまさに《第一歩》になるからなんだ。
原点だけでは何も始まらない。でも《第一歩》を踏み出すなら、そこから何か新しいことが始まる。
単位円は半径が $1$ の小さな円だけれど——
テトラ「……そして、あたしはグラフを思い浮かべたんです」
僕「グラフ?」
テトラ「はい。グラフといっても関数のグラフではなく、頂点と頂点を辺で結んだグラフです」
僕「うん、わかるよ。グラフ理論の簡単な話は以前やったことがあるから(第291回参照)。 たとえばこういうものだよね」
グラフ

テトラ「はい。 それでですね、あたしが単位円を考えたときにグラフを思い浮かべたのは、 スタートとなる頂点をこんなふうに決めれば、 そこから $1$ 歩進んだところにある頂点さんたちがイメージできたからです。 それもまた単位円みたいなものだなあ……と思いました」
スタートから $1$ 歩進んだところにある頂点たち

僕「ははあ……グラフで $1$ 本の辺を通ったところにある頂点だね。 確かに単位円みがあるなあ」
テトラ「一つのグラフには、たくさんの頂点があります。 そして頂点と頂点を結んでいる辺があります。 でも、すべての頂点が互いに結ばれているとは限りません」
僕「そうだね」
テトラ「《格子点の世界》では、位置関係ですぐに $1$ 歩がわかりました。 上下左右で隣にある点たちです。 つまり、《格子点の世界》をグラフとして考えるなら、 それぞれの頂点は、上下左右の $4$ 頂点との間に辺があると考えることができます」
《格子点の世界》をグラフとして考える

僕「確かに」
テトラ「でも、一般のグラフでは、位置関係で隣の頂点が決まるわけではありません。 そもそもグラフでは空間的な位置関係というのはないからです。あ、いえ……ないわけじゃないですね。 何というんでしょうか。どの頂点とどの頂点が隣り合っているかという隣接関係は、 辺によって決められているといいたいんですが……伝わってます?」
僕「うん、テトラちゃんの言いたいことはわかるよ。 《二つの頂点 $u,v$ のあいだに辺が存在する》ことによって《頂点 $u$ と頂点 $v$ が隣り合っている》ことを意味している——っていいたいんだよね」
テトラ「そうです、そうです」
僕「グラフといえば、村木先生からもらった《カード》を使って、 いろんな問題をいっしょに考えたよね」
テトラ「《直線国境諸国巡遊偶数回横断問題》のことですねっ!あれは驚きました(第293回参照)」
僕「よく覚えてるなあ。《機材の予約問題》というのもあったね(第295回参照)」
テトラ「はいはい」
僕「《五色定理》もあったなあ(第299回参照)! ミルカさんからも、 それからリサちゃんからも、グラフのことをいろいろ教えてもらった」
リサ「《ちゃん》は不要」
リサは僕の方をちらっと見て言った。 その間もタイピングする手は止まらない。
テトラ「ですです。 ——そんなふうに考えを進めてきて、 あたしは、グラフが《格子点の世界》を一般化していると思いました。 いわばスタートとなる頂点から $1$ 歩進んだところにある頂点全体の集合も このグラフにおける《単位円》といえそうだと気付いたとき、とっても興奮したんです。 また、新しい世界とつながった!と感じたからです。《座標平面の世界》《格子点の世界》そして《グラフの世界》……」
グラフの《単位円》

僕「うん、その気持ち、わかるわかる!」
チャームポイントの大きな目を輝かせ、大きく両手を振りながら語るテトラちゃん。
そんな彼女に引っ張られるように僕も思わず声を上げた。
彼女は、我が意を得たりとばかりにうんうんと小刻みに肯く。
テトラ「そして——そこからあたしは《グラフの探索》について考え始めました」
僕「グラフの探索……?」
テトラ「はい。スタートとなる頂点から始めて、グラフの頂点から頂点へ、 辺をたどって渡り歩いて、ゴールとなる頂点を探していく探索です」
僕「……」
テトラ「たとえば、こんなグラフがあったとします。一つの頂点をスタートとして、 別の頂点をゴールとします」
グラフの例

僕「ああ、わかったわかった」
テトラ「はい。スタートから $1$ 歩進んだ頂点、さらにそこから $1$ 歩進んだ頂点……というのを、 ゴールが見つかるまで繰り返していくんです。このグラフの例ですとスタートから $3$ 歩でゴールまで行けます」
グラフの探索、スタートから $1$ 歩目
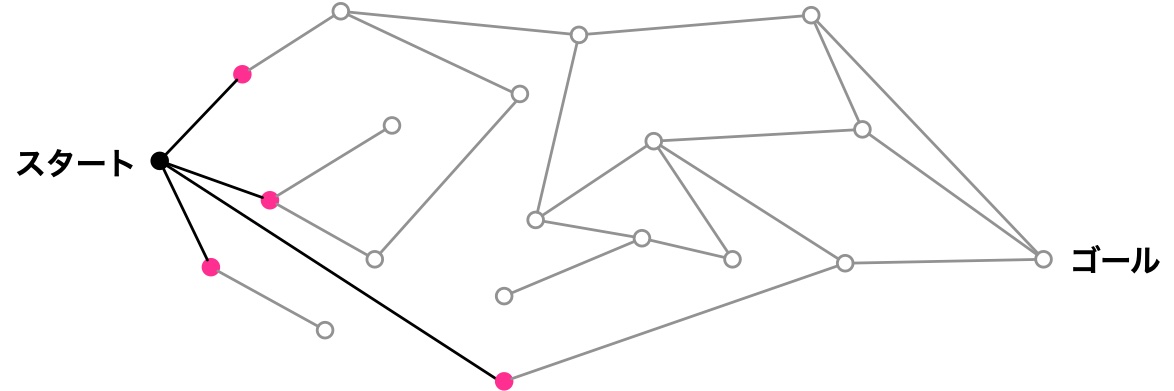
グラフの探索、スタートから $2$ 歩目

グラフの探索、スタートから $3$ 歩目でゴール
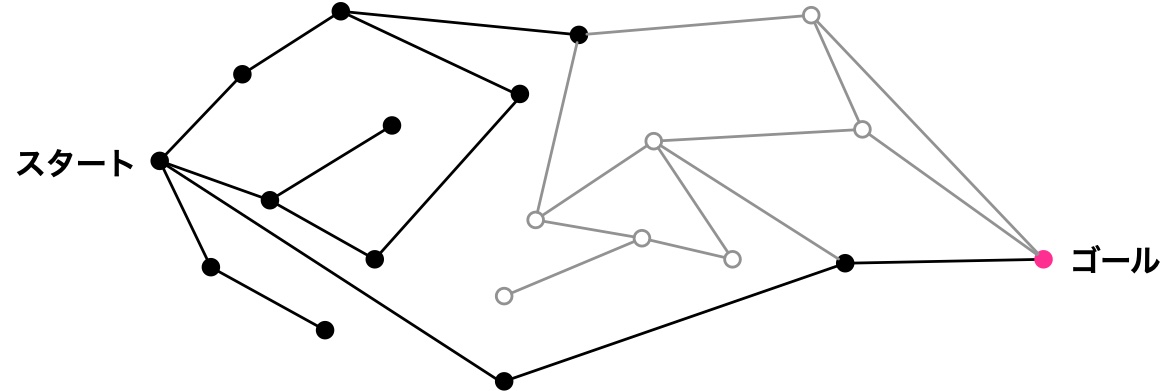
僕「それはおもしろいね! ……ところで、いま思ったんだけど」
テトラ「?」
僕「これって先日テトラちゃんが言ってた《ホイヘンスの原理》と同じ話になってるよね(第415回参照)」
テトラ「そうですっ! いま、その話をしようと思ってたところです。 さすが先輩、すぐ気付きますね」
ホイヘンスの原理
波面上の各点は新たな波源となって波を生む。
この波を素元波という。
生まれた無数の素元波に対して共通に接する面(包絡面)が新たな波面となる。 このことをホイヘンスの原理という。

※④を含む波面が⓪①②③からの素元波の包絡面として生まれる様子
僕「ぴったり同じだよね」
テトラ「はい。 波面のすべての点が波源になって、 そこから素元波が出て行くことで、次の瞬間の波面ができるという《ホイヘンスの原理》は、 波面上のすべての点が波源になるわけですが、 それは、グラフの探索でいうと、 そこまでにたどり着いた頂点を新たなスタートだと考えて、 そこから新たなグラフの探索を始めたのと基本的には同じなんですっ!」
僕「なるほどなあ……ということは、グラフの探索でも《波面》があるわけだよね。 つまりね。ゴールを探索して進んでいく途中の最前線にある頂点の集合のこと」
グラフの探索における《波面》

テトラ「そういうことになります。 グラフの探索でゴールを探し求めていく過程は、 その《波面》を少しずつ進めていく過程なんですっ!」
リサ「最短経路問題」
いままでずっと無言でキーを打っていたリサが、こちらも見ずにそう言った。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年2月16日)