![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕は高校生。ここは僕の家。中学生のいとこ、ユーリが遊びに来ている。
ユーリ「ねー、なんかおもしろいこと、ないの?」
僕「これまたいきなり」
ユーリ「いきなりじゃないもん! ユーリが来てから、お兄ちゃん、ずっと本読んでるじゃん。遊ぼーよ!」
僕「遊ぼうといってもね……」
ユーリ「クイズとか、ゲームとか、パズルとか、クイズとかないの?」
僕「クイズ二回出て来たぞ」
ユーリ「そーゆーの、いーから。お兄ちゃんの《灰色の脳細胞》から何か出したまえよ、ワトソンくん」
僕「混ざってる混ざってる。そうだなあ……」
ユーリ「その本なーに?」
僕「この本? うん、そうだ。 じゃあ、こんな連結ゲームをしようか」
ユーリ「おっ、来た来た。そー来なくっちゃ。第一戦はじまりはじまり〜……で、連結ゲームって何?」
僕「まず、紙を用意して、適当に点を打つ。打った点のことを頂点(ちょうてん)と呼ぶことにしよう。たとえば、こんなふうにたくさんの頂点を描く」
紙に頂点を描いた

ユーリ「ふむふむ。ここから星座を作る?」
僕「おっ、するどいな。違うけど」
ユーリ「違うんかい」
僕「僕とユーリで、交互に二頂点を結んでいく。たとえば、僕がこんな風に結んだとしよう。この結んだ線のことを辺(へん)と呼ぶことにする」
(1)僕が、二頂点を辺で結んだ
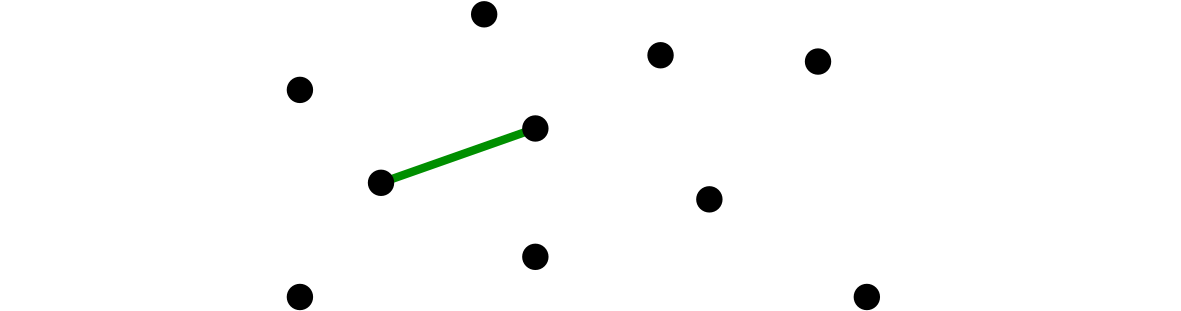
ユーリ「ふーん、次はユーリの番ってこと? どの二頂点を結んでもいいの?」
僕「うん、どの二頂点を結んでもいい」
ユーリ「じゃあ、こんな風に結んでもいい?」
(2)ユーリが、二頂点を辺で結んだ
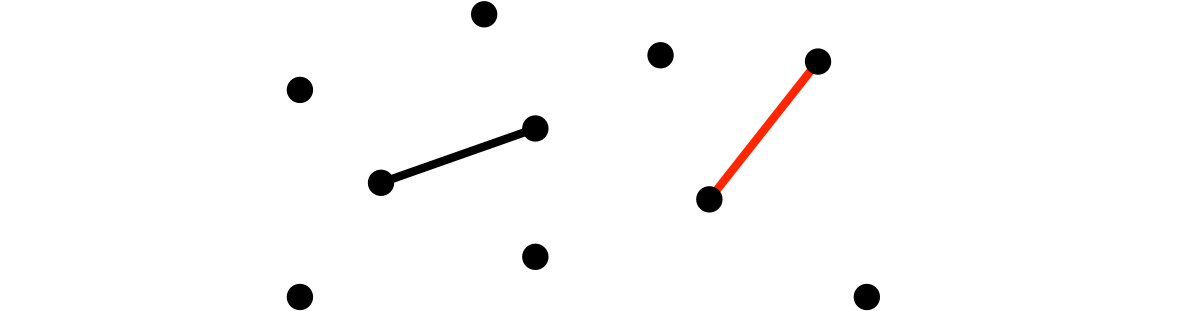
僕「いいよ。いまユーリが描いた辺はまっすぐだったけど、 辺は曲がっていてもいい。 ぐるっと回りこんでもかまわない。たとえば、僕はこんな風に結ぼう」
(3)僕が、二頂点を辺で結んだ
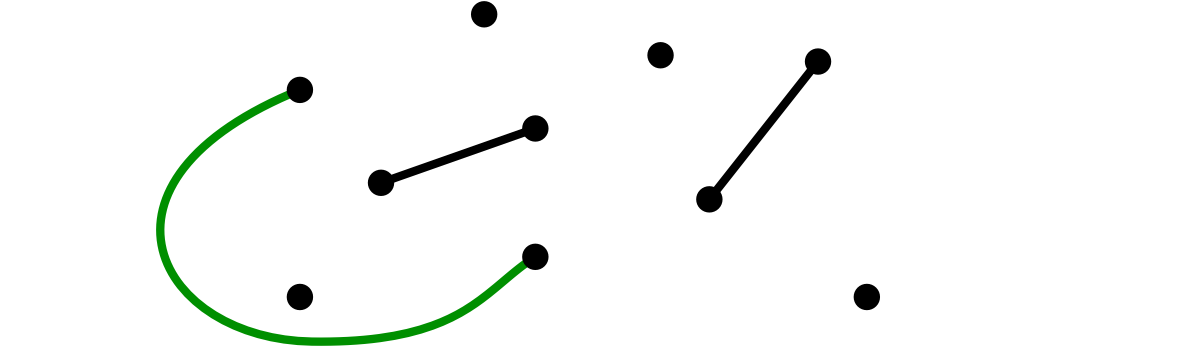
ユーリ「よくわかんないけど、ユーリはここに決めた。真実はいつもひとつ!」
(4)ユーリが、二頂点を辺で結んだ
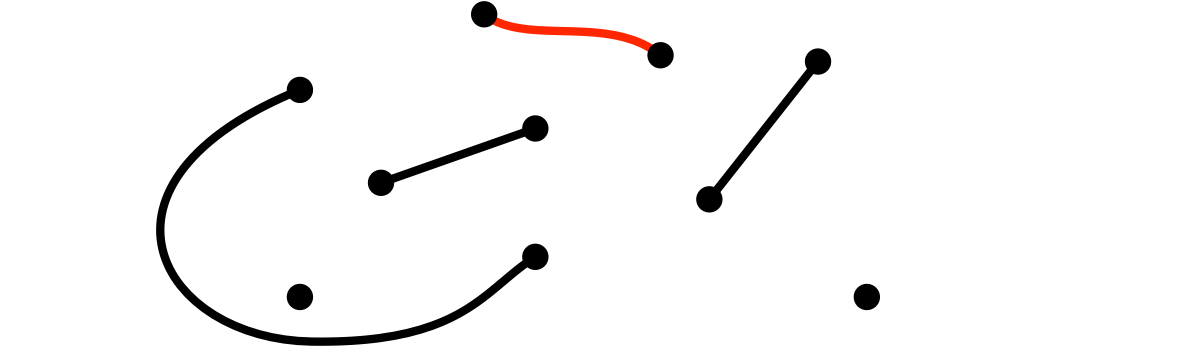
僕「コナンじゃないんだから」
ユーリ「犯人は君に決めた!」
僕「犯人を決めるなよ。じゃあ、僕はここを結ぼう」
(5)僕が、二頂点を辺で結んだ
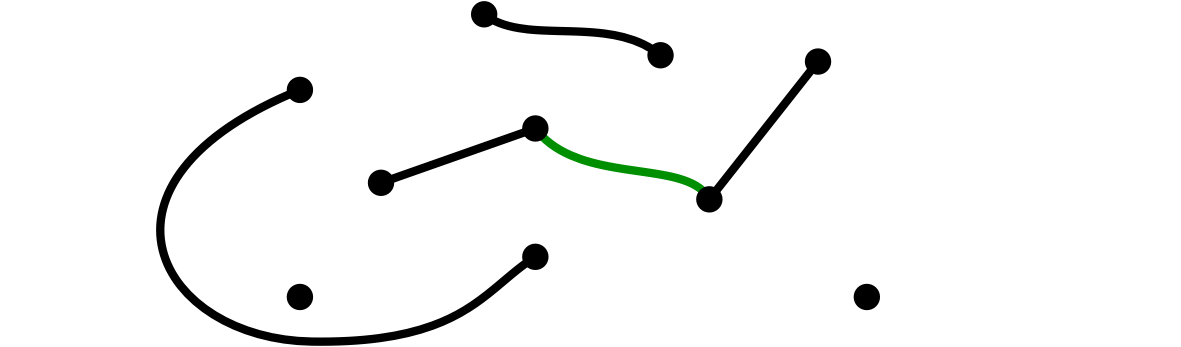
ユーリ「あっ、そーゆーふーにつないでもオッケーなんだ」
僕「いいよ」
ユーリ「ふーん……でもさ、これ、何がおもしろいの? どの二頂点を結んでもいいならゲームでも何でもないじゃん」
僕「そうだね。実は、ちょっとしたルールがある。ルールがなかったらゲームにならないからね」
ユーリ「ルール?」
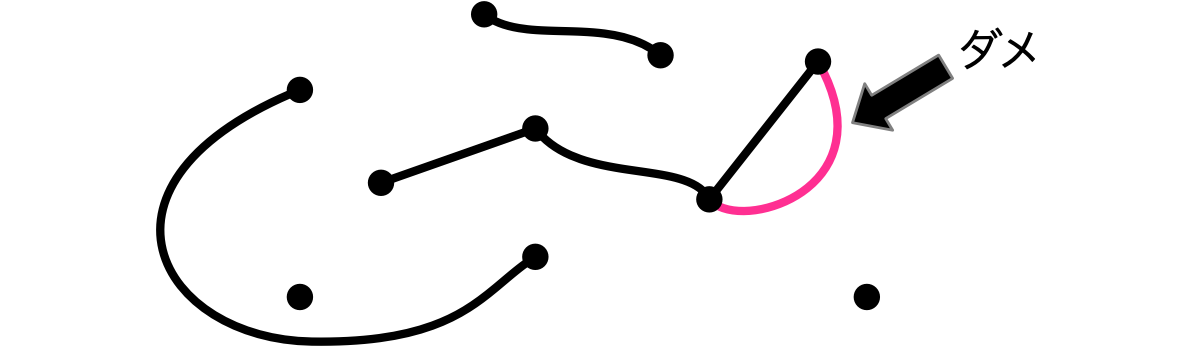
僕「辺を描くときに、すでに辺で結ばれている二頂点を結んではダメ。つまり、こういう多重になった辺を描いてはダメ。もうすでに二頂点を結んだ辺が描いてあるから」
ルール1:辺は多重にしない
ユーリ「ほほー。ちょいゲームっぽくなってきた。他にもルールあんの?」
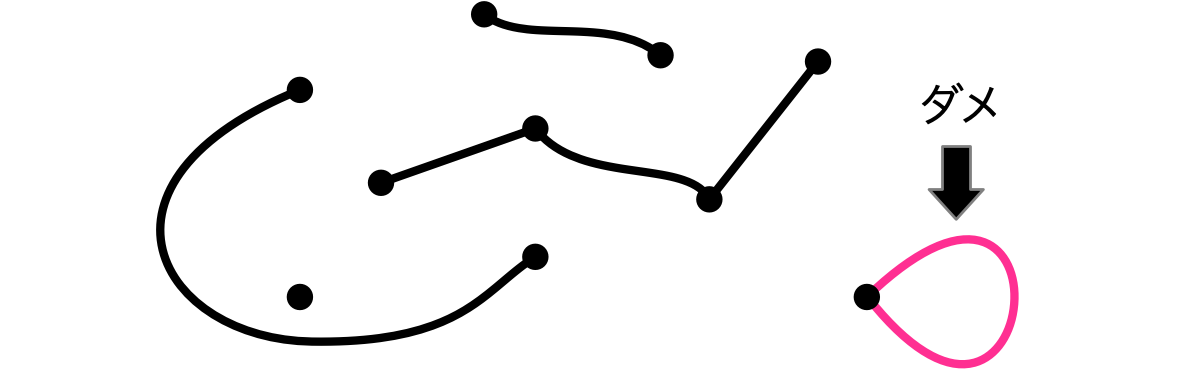
僕「あるよ。同じ頂点に戻ってくる辺はダメ。つまり、こんなふうにループを作っちゃダメ」
ルール2:ループを作らない
ユーリ「このリフジンさがたまらんなー」
僕「理不尽さって……。ゲームのルールはたいてい《○○しちゃダメ》だよね。たとえばサッカーではボールを手で持っちゃダメ」
ユーリ「ゴールキーパーは手で持ってもいーじゃん。てか、話を先に進めてくれたまえ、エラリイくん」
僕「それから最後のルールとして、サイクルを作っちゃダメ」
ユーリ「サイクルって何?」
僕「こういうもの」
ルール3:サイクルを作らない
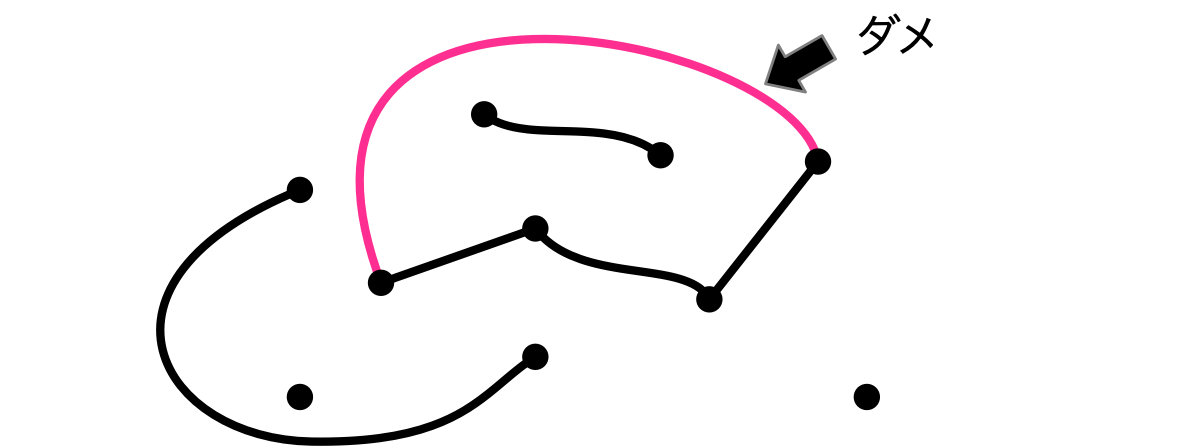
ユーリ「これがサイクル?」
僕「ひとつの頂点から辺をたどって最初の頂点まで戻って来ることができる。そんなふうに選んだ辺の集まりがサイクル。サイクルができるような辺を描いてはダメ」
サイクル
ユーリ「ぐるっと回れちゃダメってことね。さらなる理不尽さが加わった!」
僕「いま言った三つのルールを守りながら、交互に辺を描いていく。そして描けなくなったら負け。それが連結ゲームなんだ」
ユーリ「りょーかい! 辺は多重にしない。ループを作らない。サイクルを作らない。真夜中を過ぎたら森に入らない」
僕「ルールを勝手に作らない」
ユーリ「んじゃ、第一戦再開!」
僕「僕はもう描いたから、次はユーリだよ」
ユーリ「うーん……どこを結ぼーかなー。じゃ、ここ」
(6)ユーリが、二頂点を辺で結んだ
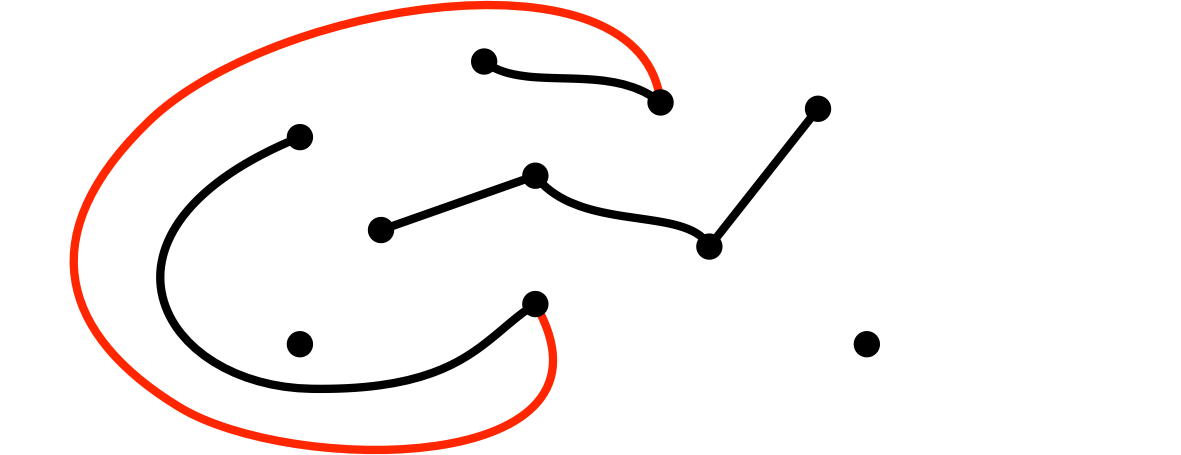
僕「ずいぶん回り込んだなあ!」
ユーリ「ルールは守ってるっしょ?」
僕「そうだね。じゃあ、僕はここ」
(7)僕が、二頂点を辺で結んだ
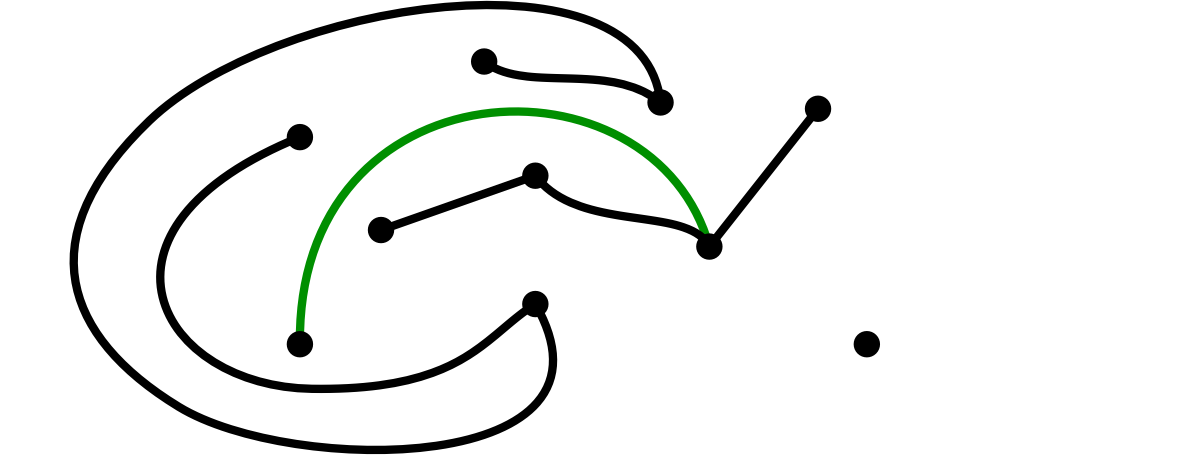
ユーリ「そっか、間に入り込む手もあるんだ……じゃ、ユーリはここ」
(8)ユーリが、二頂点を辺で結んだ
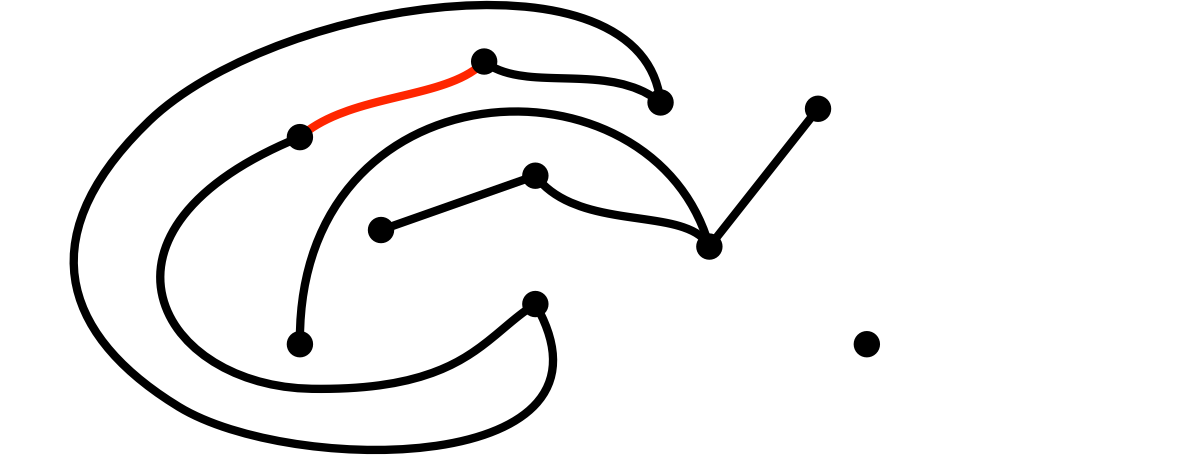
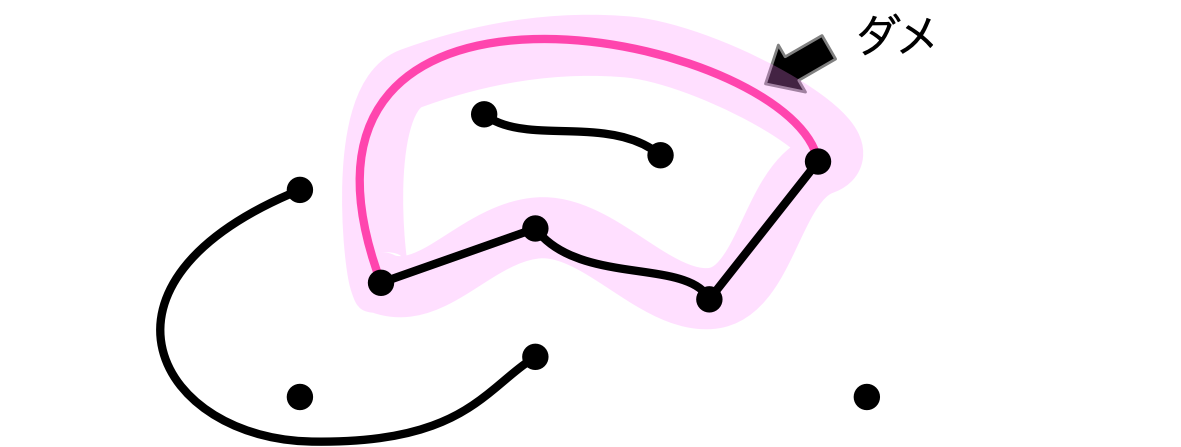
僕「いやいや、それはダメだよ」
ユーリ「なんで? どこ結んでもいいんでしょ?」
僕「だって、ルール3に違反している。サイクルができてるからね。全体をよく見ないとサイクルを見落とすよ」
サイクルができてしまった
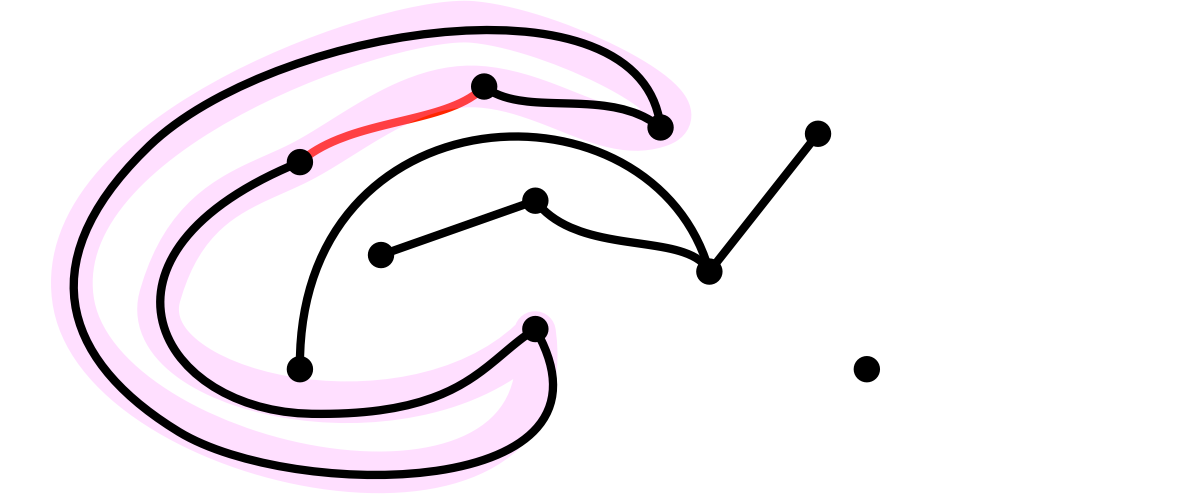
ユーリ「あっ、ほんとだ。紛らわしーにゃあ」
僕「回り込んで描いたのはユーリだからね、言っておくけど」
ユーリ「へいへい、そーですねっと。……んじゃ、ここ」
(8A)ユーリが、二頂点を辺で結びなおした
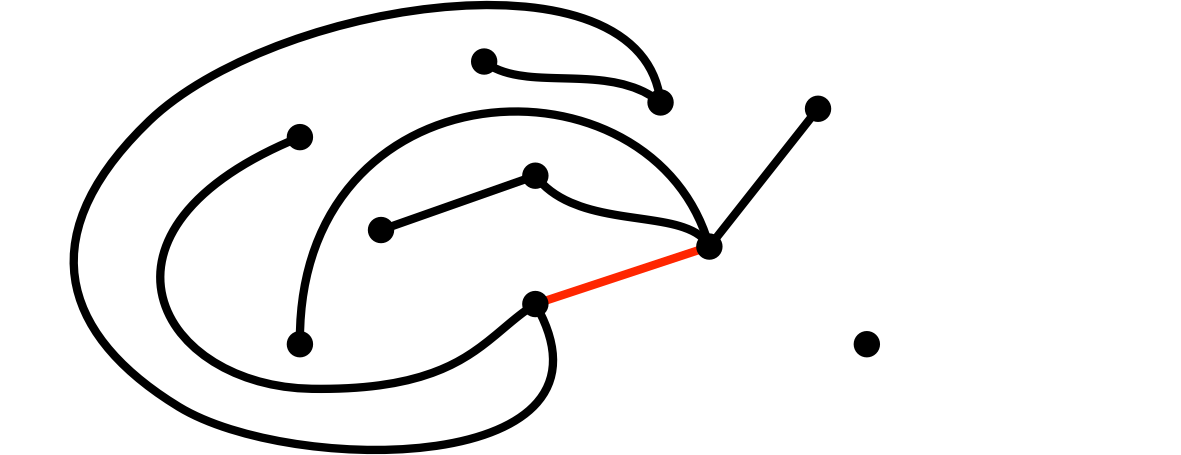
僕「なるほど。じゃあ、僕はここ」
(9)僕が、二頂点を辺で結んだ
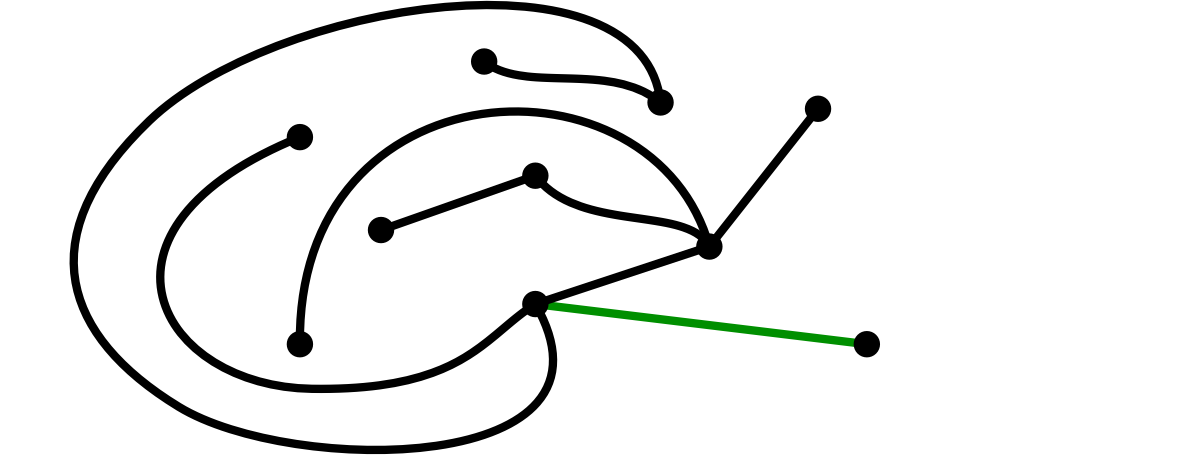
ユーリ「んー、じゃユーリは……」
僕「どこを結ぶ?」
ユーリ「ユーリはね……ありゃ? ちょっと待って。 あーっ! やっぱりダメかーっ!」
僕「うん、これで第一戦は僕の勝ちだね」
第一戦、ユーリの負けが確定
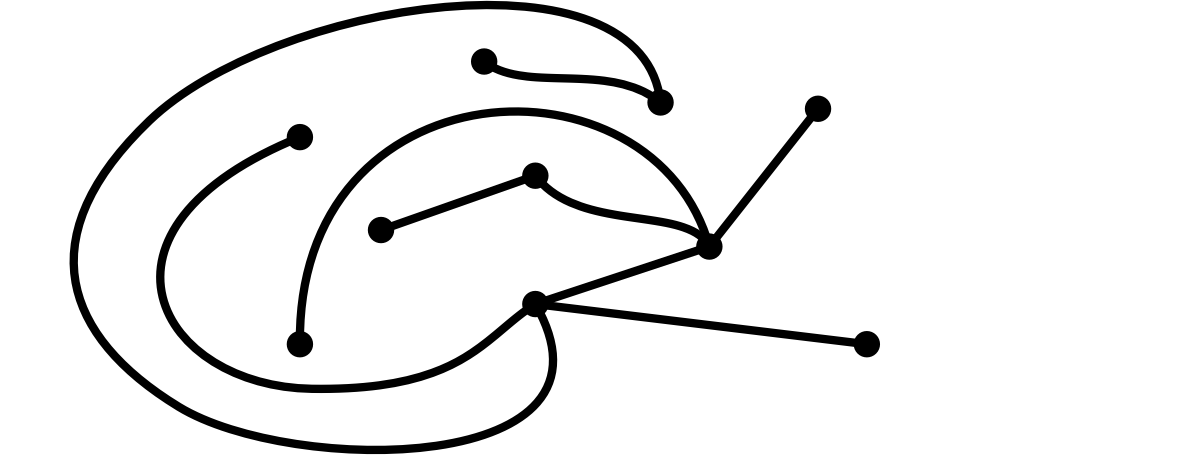
ユーリ「むー、ぐるっと回ったのが敗因かにゃあ……」
僕「こんなゲームだよ。わかった?」
ユーリ「もっかいやる! 今度は勝つ! ユーリ先攻でもいい?」
僕「うん、ユーリ先攻でいいよ。じゃあ、第二戦は新しい紙でやり直そう」
新しい紙に頂点を描いた

ユーリ「今度はすなおに行くぞよ」
[1]ユーリが、二頂点を辺で結んだ
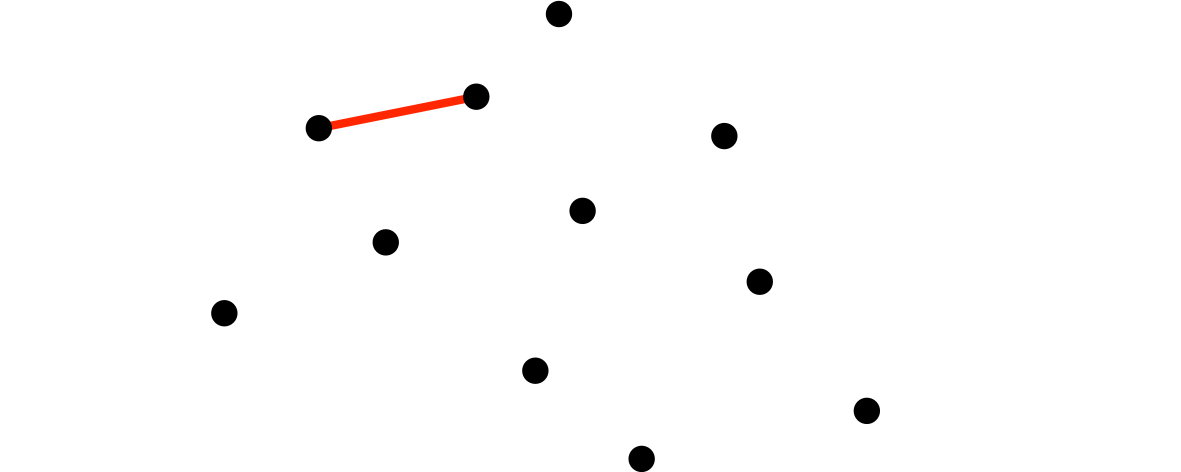
[2]僕が、二頂点を辺で結んだ
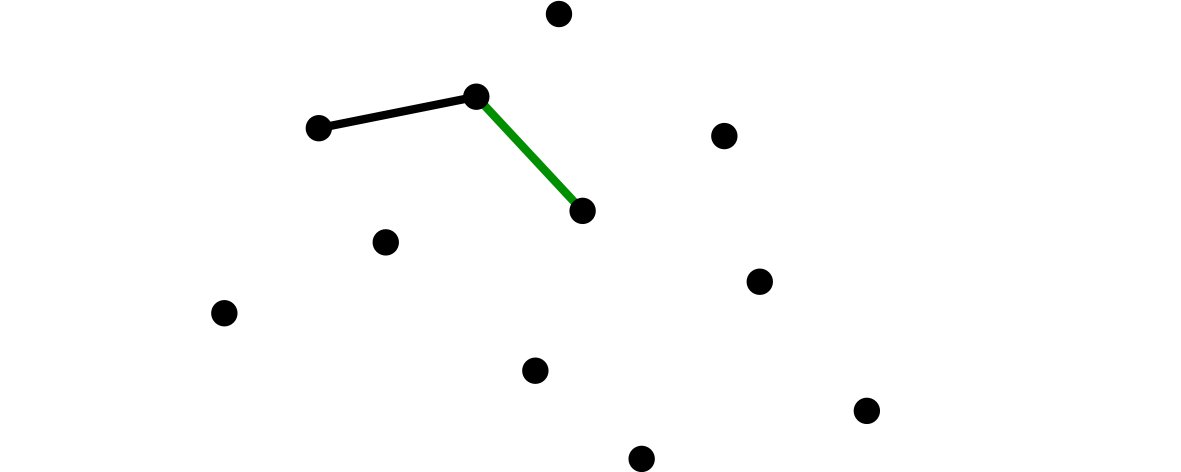
[3]ユーリが、二頂点を辺で結んだ
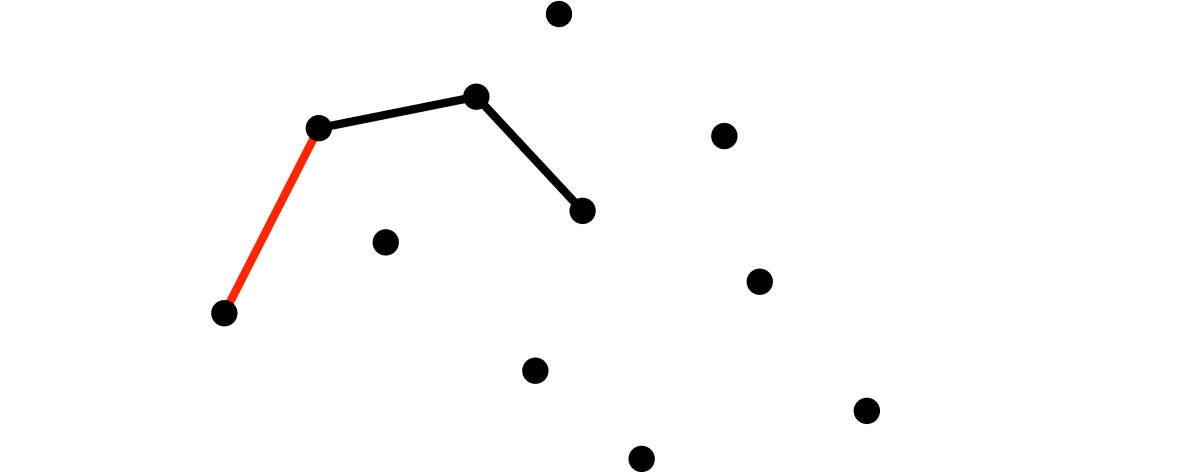
[4]僕が、二頂点を辺で結んだ
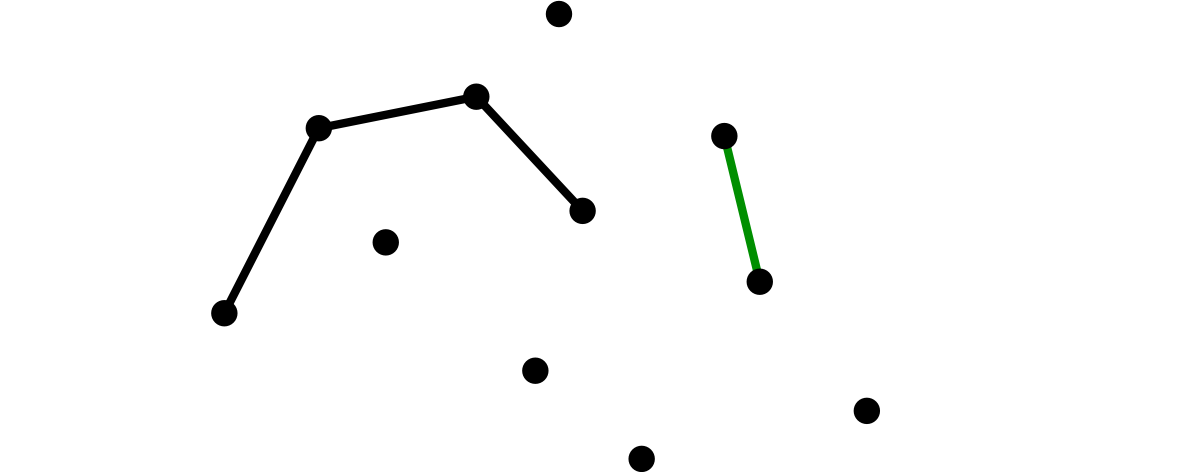
こんなふうにして、ユーリと僕は交互に辺を描いていった。僕が[8]を描いたところで、ユーリが思考モードに入った。
[8]僕が、二頂点を辺で結んだ
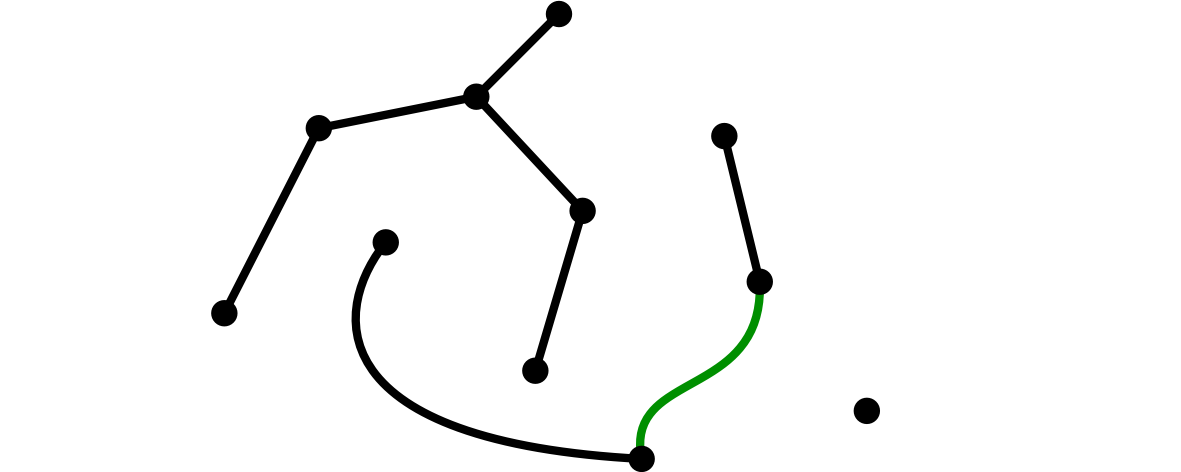
ユーリ「……」
僕「どうした? 次はユーリの番だよ」
ユーリ「……また負けそう」
僕「そうかな?」
ユーリ「うん……絶対負ける。だってね、次ユーリが描いて、その次お兄ちゃんが描いたら、もう描けなくなるもん。絶対!」
僕「絶対?」
ユーリ「絶対。だって……む? むむ?」
そこで、ユーリは顔をしかめる。
どうやら、長考モードに入ったようだ。
さてさて、ユーリは気がつくだろうか。

僕「……」
ユーリ「お兄ちゃん、第一戦の紙見せて」
僕「ん? これのこと?」
第一戦、ユーリの負けが確定したときの紙

ユーリ「第一戦のときは頂点が $10$ 個だった。第一戦って、何気にお兄ちゃんが先攻だったよね」
僕「そうだね。ルール説明もあったし」
ユーリ「第二戦のこれは頂点が $11$ 個ある。第二戦って、お兄ちゃんは後攻だった……」
第二戦、ユーリの負けが確定しそうな紙
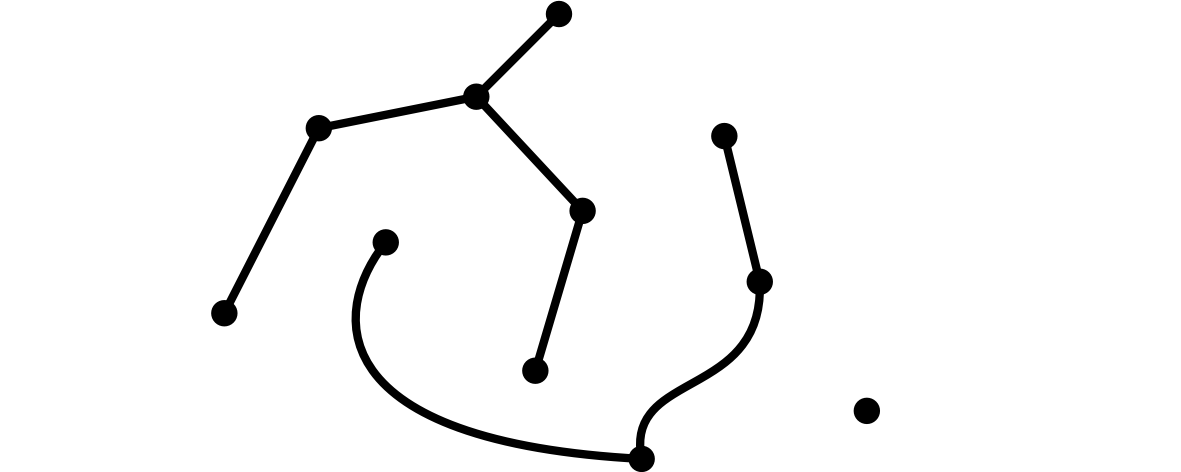
僕「うん。ユーリが先攻をやりたいと言ってたから」
ユーリ「もひとつ質問いいかにゃ。 第二戦では、ユーリが先攻になることが決まってから、 お兄ちゃんが頂点を描いたよね。先攻・後攻が決まった後で頂点の個数が決まった……?」
僕「ユーリのような勘の良い……」
ユーリ「テンプレいいから。もーわかった! この連結ゲーム、最初の頂点の数で勝敗決まるんでしょ!」
僕「その通り。よく見抜いたなあ」
ユーリ「ちっちっち。簡単な推理だよワトソンくん。 それに、お兄ちゃんがずるっこするのはこれが初めてじゃないからね」
僕「そうだっけ」
ユーリ「そーだよー! よくあるパターンじゃん!」
僕「それはさておき、頂点の数で最初から勝敗が決まるというけど……もうちょっと詳しく指摘してほしいなあ」
ユーリ「んー……ユーリの勘では、頂点が偶数個のときは先手必勝で、 頂点が奇数個のときは後手必勝なんじゃね?」
ユーリの推理
《連結ゲーム》では、最初に描いた頂点の数で勝者が決まる。
僕「なるほど。それがユーリ名探偵の推理なんだね」
ユーリ「そーだよん。だから、お兄ちゃんは点を $10$ 個描いたときは先攻を選んだんでしょ。偶数だから。 そして、ユーリが先攻になったときは、点を $11$ 個描いた。それは自分が勝つため!」
僕「名推理だ!」
ユーリ「真実はいつもひとつ! 整数はいつも偶数か奇数!」
僕「でも、頂点が $10$ 個のときと、 $11$ 個のときの二戦しかやってないよね。その他の数でも《必ず》勝敗が決まると言える?」
ユーリ「言えると思うよん」
僕「それから、ポイントは頂点の数じゃなくて、頂点の配置の可能性はないかな。頂点が偶数か奇数かだけで《必ず》勝敗が決まる?」
ユーリ「うー、決まると思うけど……」
僕「それから、辺の描き方で勝ったり負けたりするかもしれないよね。 ほんとうに数だけで《必ず》勝敗が決まる?」
ユーリ「ぐぬぬ……ちょっと待って。なぜにユーリが責められるのじゃ。わらわに何を求めておるのじゃ」
僕「キャラ壊れてるぞ。うん、つまりね。《必ず》というためには、証明したくなるよね、ってこと」
ユーリ「証明? 証明って数学の証明?」
僕「そうだよ。数学の証明。頂点が何個でも、配置がどうであっても、辺の描き方によらず……頂点が偶数個ならば先手必勝で、 頂点が奇数個なら後手必勝であることを証明してしまえばいい」
ユーリ「頂点に辺を描くのが、数学なの?」
僕「そうだよ。数学で扱うことができる。グラフ理論だね!」
ユーリ「ぐらふりろん。……でも、ぐにゃぐにゃだよ?」
僕「ぐにゃぐにゃ?」
ユーリ「辺はいくら曲がってもいいし、回り込んでもいい。 そんなぐにゃぐにゃなのに、数学なの?」
僕「ああ、そういうこと? うん、そうだね。 辺はどんなに曲がっていてもいい。 数学で図形を扱うときは三角形や円や長方形のように、何ていうか『きちんとした図形』がよく出てくるけれど、 それだけが数学じゃないよ」
ユーリ「あっ、あっ、あっ、えーと……ケーニッ?なんとかの橋だ!」
僕「もしかして、ケーニヒスベルクの橋のこと? 一筆書きの問題だね」
ユーリ「それそれ! 一筆書きでも、道を曲げてもよかったよね。この連結ゲームとおんなじだ!」
僕「その通りだね。まさにそれだよ」
【宣伝タイム】
テトラ「ケーニヒスベルクの橋から始まるユーリちゃんと先輩の楽しい対話は、 ぜひ、こちらの一冊『ポアンカレ予想』をごらんくださいっ! 第1章「ケーニヒスベルクの橋」はWebで立ち読みができます(ぺこり)」
ユーリ「宣伝テトラさん……」
僕「一筆書きの問題は、グラフ理論でよく出てくる話題のひとつ。 グラフ理論では、頂点同士がどんなふうにつながっているかが大事なんだ。 どの頂点とどの頂点が隣接しているかが大事であって、 辺がまっすぐか曲がっているかは気にしない」
ユーリ「りんせつ?」
僕「隣り合っているってこと。頂点Aと頂点Bが辺で結ばれているようすを考えると、 頂点Aと頂点Bが隣り合っているといえるよね。そういう状況を《隣接している》と呼んだんだ」
ユーリ「ところで、どーやって証明するの? 辺を描いていく連結ゲームで、頂点が偶数個だったら先手必勝、奇数個だったら後手必勝……それを証明するって、 いったいどーすんだろ。頂点は何個描いても関係ないわけでしょ。 $5000$ 兆個描いてもいいわけだし」
僕「$5000$ 兆個の頂点だったら、先手必勝になるよ。偶数だからね」
ユーリ「どう証明すんの?」
僕「うん。証明する前にやるべきことがあるね。 それは《小さい数で試してみる》ってことだよ」
ユーリ「さっきやった。 $10$ 個」
僕「もっとずっと少ない数で試してみよう。たとえば、頂点が $1$ 個の場合」
ユーリ「頂点が $1$ 個! うわっ、しょーもない連結ゲーム!」
頂点が $1$ 個の場合

僕「後手必勝になるかな?」
ユーリ「えっと……あー! そーゆーことか! うん、後手必勝だよ。 だって、ループを作っちゃいけないんでしょ? 《ルール1》だ。 頂点が $1$ 個しかないから、もう辺は描けない。だから、先手になったら負け。何ということでしょう」
頂点が $1$ 個の場合、辺を描くとループになってしまう

僕「うん、頂点が $1$ 個の場合は後手必勝。では、頂点が $2$ 個の場合はどうかな?」

ユーリ「うん、頂点が $2$ 個だったら、先手必勝になるね。だって、先手が辺を描いたら、後手はもう描けないもん」

僕「そうだね。もしも、ループはダメだし、無理に辺を描いたら、辺が多重になってしまう。《ルール1》に反するわけだね」

ユーリ「ははーん……」
僕「何か気がついた?」
ユーリ「頂点が $1$ 個の場合、頂点が $2$ 個の場合と来たら……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第291回終わり)
(2020年6月5日)