![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは、パスカルの三角形を使って楽しい数学トークを行っている。
パスカルの三角形の中に組み合わせの数が出てくるのはどうしてかというユーリの疑問をきっかけにして(第391回参照)、 僕たちは、組み合わせの数についておさらいした(第392回参照)。
ユーリ「……パスカルの三角形で、二つの数を足すと《組み合わせの数》が出てくる理由、わかったかも!(第392回参照)」
僕「それはよかった」
ユーリ「最後の一つを選ぶか選ばないかで場合分けしておいて、その両方を足す——あれ、でもおかしくない?」
僕「何かおかしなところあった?」
ユーリ「だって……二つの数を足すところはわかったけど、 $1$ は?」
僕「$1$ って? ああ、両端の $1$ のことかな? パスカルの三角形は上から作っていくけど、各行についてこんな手順を繰り返す。
パスカルの三角形と《組み合わせの数》の表
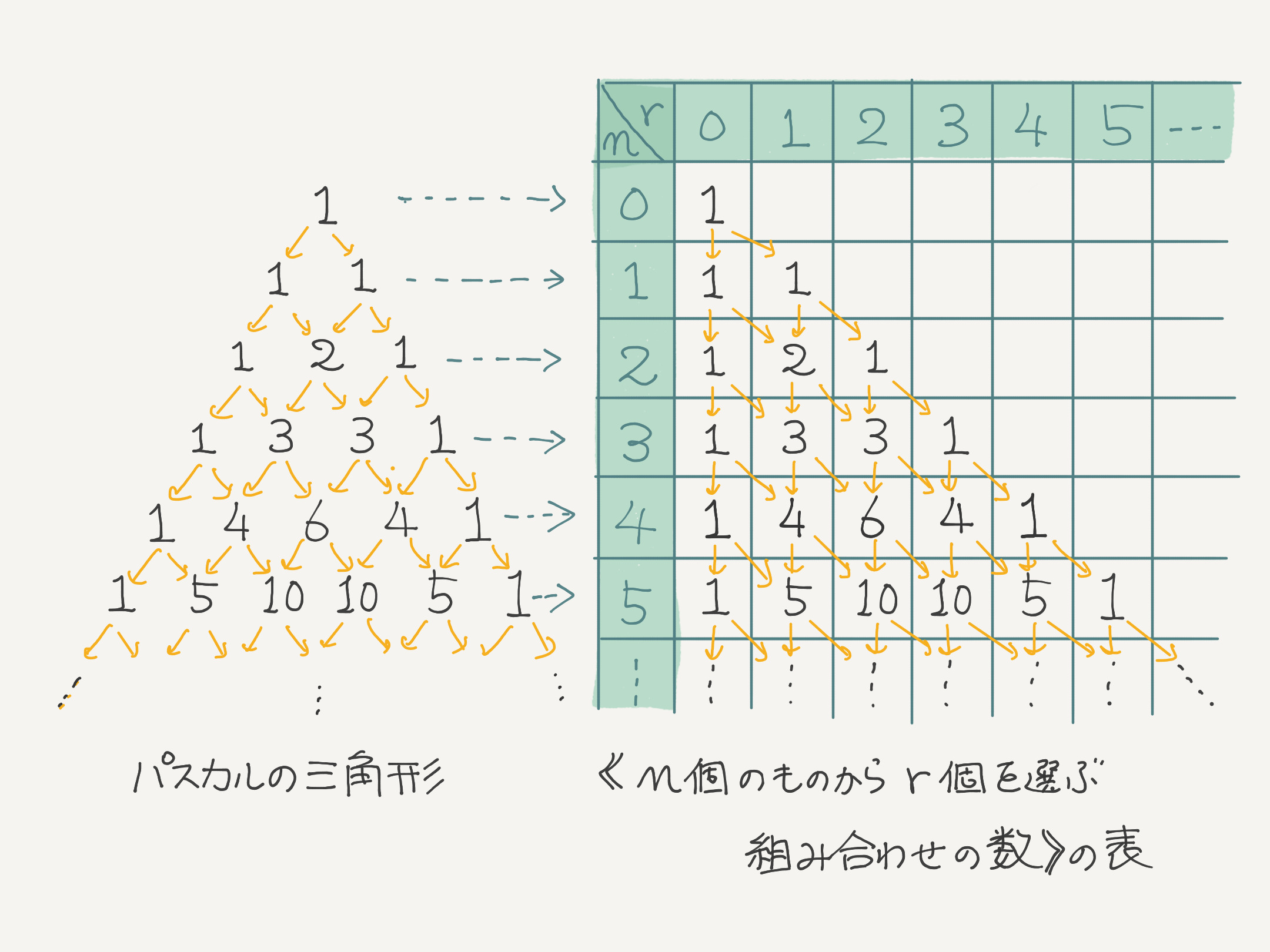
ユーリ「……」
僕「左端の $1$ は全部《$n$ 個のものから $0$ 個を選ぶ組み合わせの数》で、 右端の $1$ は全部《$n$ 個のものから $n$ 個を選ぶ組み合わせの数》になる」
左端の $1$ と右端の $1$

ユーリはしばらくこの表を眺めていた。
ユーリ「……あのね、《$n$ 個から $n$ 個を選ぶ組み合わせの数》が $1$ になるのはわかる。 《ぜんぶ選ぶ》ってことだから、そりゃ $1$ 通りだよね。 でも、《$n$ 個から $0$ 個を選ぶ組み合わせの数》も $1$ なの? 何も選んでないんだよ?」
僕「うん、そうだね。 《$0$ 個を選ぶ》というと何も選んでないみたいに感じるけど、 《$n$ 個を捨てている》と考えれば、何を捨てるかを選んでいると考えられる。 つまり《$n$ 個から $0$ 個を選ぶ組み合わせの数》は《$n$ 個から $n$ 個を捨てる組み合わせの数》に等しくなるんだね」
ユーリ「あー、そりゃそーか。いまの話、おもしろいね。《どれを選ばないか》を選んでるんだ!」
僕「そういうこと。その話は、パスカルの三角形で上から降りてくる矢印を考えてもわかるよ(第392回参照)」
ユーリ「ほほー?」
僕「たとえば、てっぺんから $4$ 個の矢印をたどって降りてくるときに《$4$ 個から $\RA$ を $0$ 個選ぶ》のは、 《$4$ 個から $\LA$ を $4$ 個選ぶ》のと同じことになる。そしてそれはどちらも $1$ 通り」
《$4$ 個から $\RA$ を $0$ 個選ぶ》のは《$4$ 個から $\LA$ を $4$ 個選ぶ》のと同じ
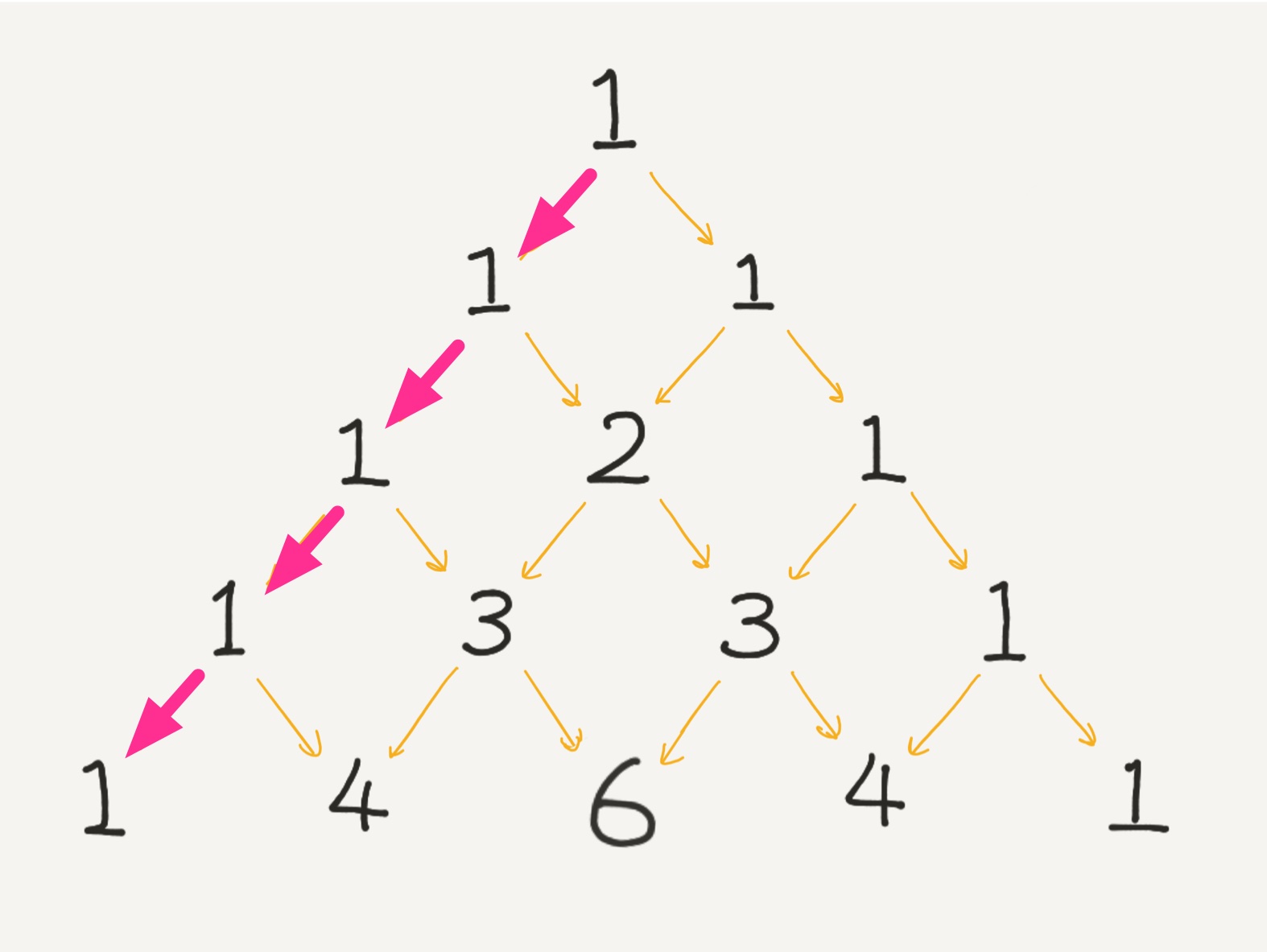
ユーリ「ふんふん。 それって、反対を考えても同じだね」
僕「反対って?」
ユーリ「$\RA$ と $\LA$ を反対にするの。 《$4$ 個から $\LA$ を $0$ 個選ぶ》のは《$4$ 個から $\RA$ を $4$ 個選ぶ》のと同じでしょ?」
《$4$ 個から $\LA$ を $0$ 個選ぶ》のは《$4$ 個から $\RA$ を $4$ 個選ぶ》のと同じ
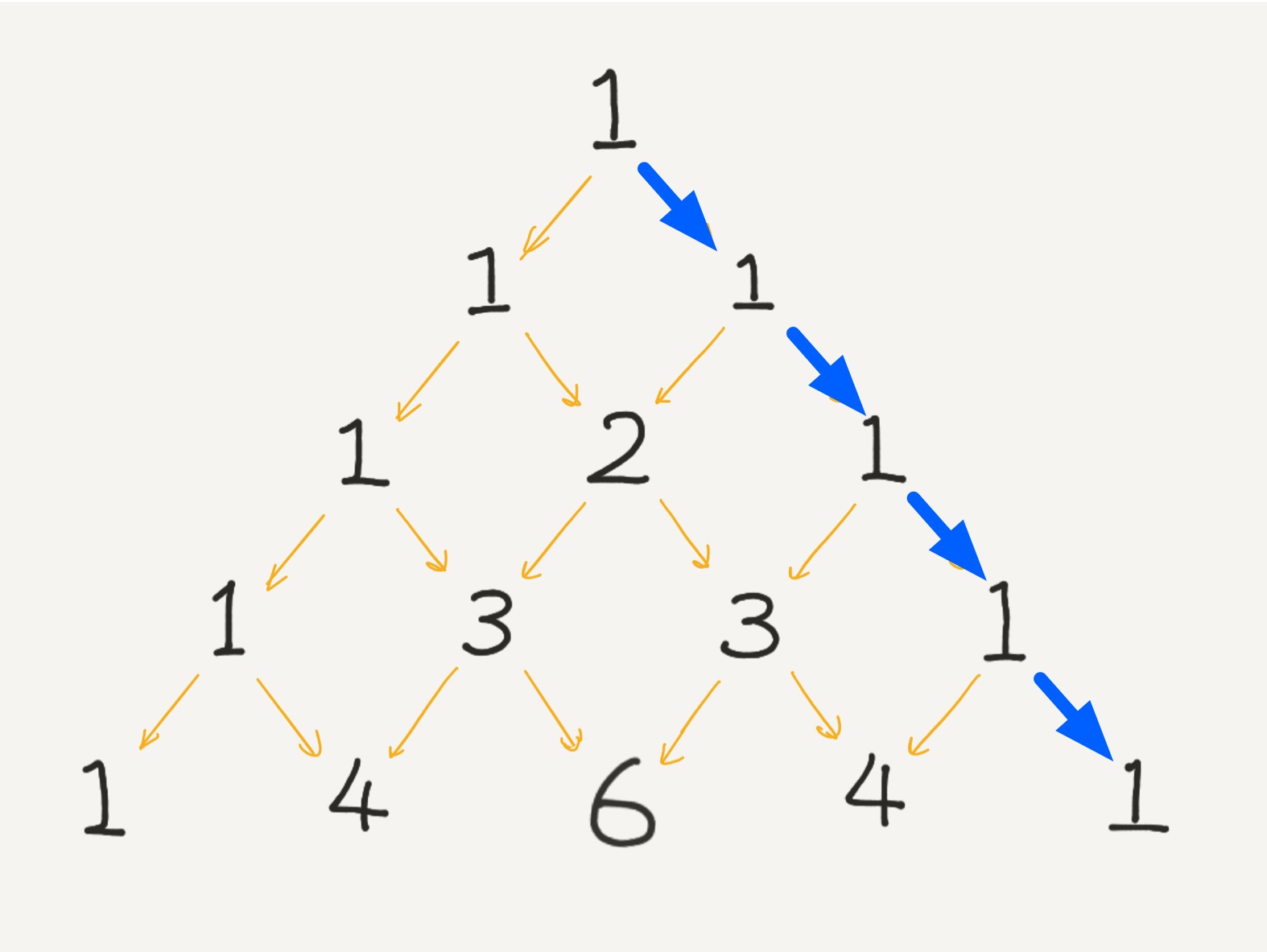
僕「$\RA$ と $\LA$ を交換して考えたんだね、その通り。 そう考えると、パスカルの三角形が左右対称になるのも納得がいくね。 《組み合わせの数》で考えると、
《$n$ 個から $r$ 個選ぶ組み合わせの数》は《$n$ 個から $n-r$ 個選ぶ組み合わせの数》に等しい
からね」
ユーリ「$n-r$ 個選ぶのは $r$ 個捨てるものを選ぶのと同じことだから」
僕「そう。まあ、左右対称なのはパスカルの三角形の作り方からもわかるけどね」
ユーリ「《組み合わせの数》の表にしちゃうと、左右対称になんない」
僕「《組み合わせの数》の表は、数を左に寄せているからね。 でも、表の各行をよく見ると、ちゃんと左右対称だよね」
ユーリ「そりゃそーか。 $1$ も、 $1\quad1$ も、 $1\quad2\quad1$ も、 $1\quad3\quad3\quad1$ も全部左右対称……おっ、 ねーお兄ちゃん! てっぺんの $1$ がおもしろい!」
僕「?」
ユーリ「《組み合わせの数》の表で見ると《$0$ 個から $0$ 個選ぶ組み合わせの数》が $1$ になるってことだよね! 何もないところから何も選ばないやり方を $1$ 通りって数えるの、 すんごくおもしろい! 透明人間を捕まえたみたい!」
僕「マニアックなところに気付くなあ。確かにそうだね。 《$0$ 個から $0$ 個選ぶ組み合わせ》というものにどういう意味付けをするか——そして意味付けをした方がいいのかどうか——は微妙なところはあるけれど、 《$0$ 個から $0$ 個選ぶ組み合わせの数》を $1$ と考えるのが規則的なのは確かだね」
《$0$ 個から $0$ 個選ぶ組み合わせの数》は $1$ 通り

ユーリ「ねーお兄ちゃん。ぜんっぜん違う話、始めてもいーい?」
僕「ダメ」
ユーリ「うわなにそれいじわる!」
僕「どうせ『ダメ』って言っても始めるだろ、ユーリは」
ユーリ「ま、そーなんだけどね」
僕「それで? 全然違う話って?」
ユーリ「パスカルの三角形の話」
僕「全然違わない話」
ユーリ「違うって! ……あのね、《組み合わせ》を考えるときって、 選ぶものの順序は気にしないんだよね」
僕「そうだね。《組み合わせ》を考えるとき、 $1,2,3,4$ の $4$ 枚のカードから、 $2,3$ を選ぶのと $3,2$ を選ぶのは区別しない。 $2$ を先に選んでも、 $3$ を先に選んでも $2,3$ と $3,2$ を同じ《組み合わせ》だと考えるわけだね」
$4$ 枚のカードから $2,3$ を選ぶのと、 $3,2$ を選ぶのは《組み合わせ》としては同じ

ユーリ「でも、パスカルの三角形を矢印で降りてくるときって、順序を気にするよね? それなのに《組み合わせ》なの?」
僕「なるほど……ユーリが言うのはこういう意味だね。 たとえば、《$4$ 個から $2$ 個を選ぶ組み合わせ》を考えるときに、 $\LA\LA\RA\RA$ と $\RA\LA\RA\LA$ は $2$ 個の $\LA$ と $2$ 個の $\RA$ の順序が変わっただけなのに、 違う道筋だと考える。順序を気にしているようなのに、 どうして《組み合わせ》なのか?」
$\LA\LA\RA\RA$ と $\RA\LA\RA\LA$

ユーリ「それそれ。順序を気にしないって、何だかわかんなくなっちゃった」
僕「なるほどね。確かにちょっと紛らわしいところはあるかな……」
ユーリ「うん。ある」
なるほどなあ……どんなふうに整理すればすっきりするだろう、と僕はしばし考える。

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2023年6月2日)