![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ねー、お兄ちゃん。ユーリはそろそろ退屈してますよ?」
僕「そのフレーズ、気に入ってるの?」
ユーリ「気に入ってる」
僕「こないだも言ってたよね。 僕がユーリを退屈させているような、まるで僕が義務を怠っているような、 暗黙のプレッシャーを掛けてくるような、謎のフレーズ」
ユーリ「お兄ちゃんには、ユーリを退屈させない義務があるのじゃ。おもしろい話をせよ!」
僕「すでに暗黙ですらなくなってる!」
ユーリ「あははー」
ここは僕の部屋。
いつものように、 いとこの中学生ユーリが遊びに来ている。
近所に住んでいる彼女は、小さい頃からいっしょに遊んでいる仲良しで、 僕のことをいつも《お兄ちゃん》と呼ぶ。
僕「ユーリこそ、何かおもしろい話はないの? ほら、ボーイフレンドとよくやってる《数学対決》は最近どう?」
ユーリ「あいつのこと? ボーイフレンドとかそーゆーんじゃないからね、言っとくけど。 んー、最近はあんまり問題出してないにゃあ、そーいえば」
僕「ねえ、ユーリ。お兄ちゃんはそろそろ退屈してますよ?」
ユーリ「真似するなー!」
僕「あはは」
ユーリ「こないだテトラさんが『360回でぐるっとひとまわりみたい』って言ってたよね(第359回参照)」
僕「そうだね。360という数字は、360度という角度を連想するからだと思うけど。 『360度』は比喩的にも使われるね。全体を見渡すことや、すべての方向を表すときに」
ユーリ「うん」
僕「テトラちゃんは、そういう動きがある感じが好きなのかもね。ほら、ちょっと、バタバタしてるところもあるし」
ユーリ「手とか足とかぐるぐる回したりするよね」
僕「いやいや、さすがに足は回さんでしょう。 ……ぐるっと回すといえば、正方形をコンパスで描くって話を持ち出してきたことがあったよ(第89回参照)」
ユーリ「テトラさんが? 正方形ってコンパスで描けんの? コンパスって円を描くものでしょ?」
僕「そうだね、コンパスは円を描くために使う。 テトラちゃんが話していたのはぐるっと回すようにして線を描く話なんだ。 テトラちゃんはイメージで話していたけど、 ミルカさんがそれに関連して極座標を教えてくれた」
ユーリ「ミルカさまが! それ、教えてちょーだい!」
……こんなふうにして、 僕とユーリの楽しい《数学トーク》が始まった。
僕「まずはざっくりと極座標のアイディアを話すね」
ユーリ「うん!」
僕「長さが $r$ の線分 $OP$ を用意する。 点 $O$ は平面上に固定しておいて、点 $P$ をぐるっと回す。 線分 $OP$ の長さは $r$ のままだよ。そうするとこんな風に点 $P$ は円を描くことになる」
点 $P$ をぐるっと回す
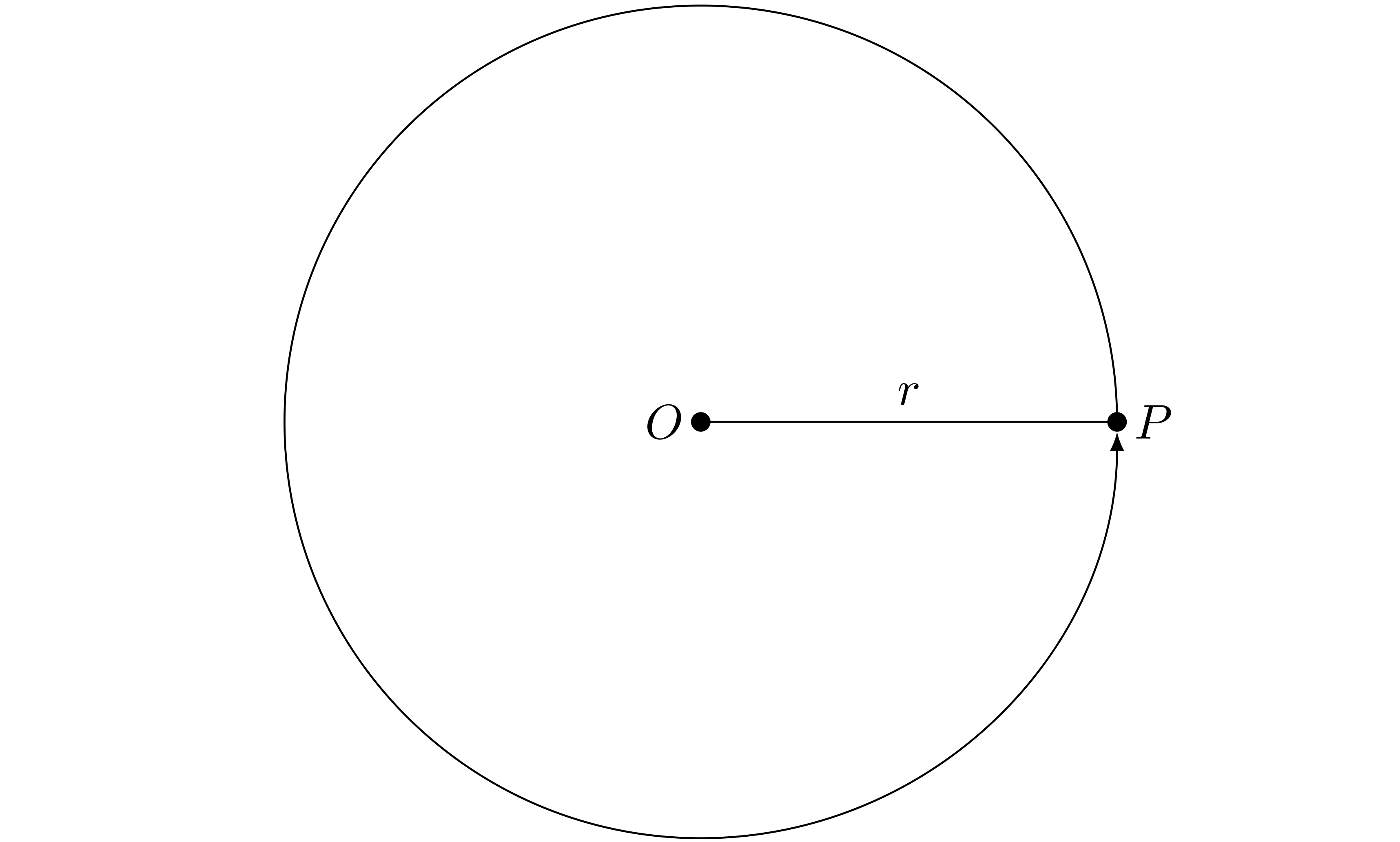
ユーリ「それってコンパスの話じゃないの? 中心が $O$ として、半径 $r$ で円を描いてる」
僕「そうだね。これはコンパスと同じこと。それは線分 $OP$ の長さ $r$ を一定の値にしているから。 じゃあ、点 $P$ を回すとき、回した角度に応じて長さを変えたらどんな図形を描くことになるだろうか」
ユーリ「そりゃ……そりゃ、どんなふうに長さを変えるかに寄るんじゃない?」
僕「そういうことになるよね。 どの角度のときに、点 $O$ からの長さをどうするか、 それによって点 $P$ の位置が決まることになる。 つまり、
点 $O$ からの長さ $r$ と、角度 $\theta$ を使って、平面上の一点 $P$ を表す
と考える。 長さ $r$ と角度 $\theta$ を使う。これが極座標の基本的アイディアになる」
極座標の基本的アイディア
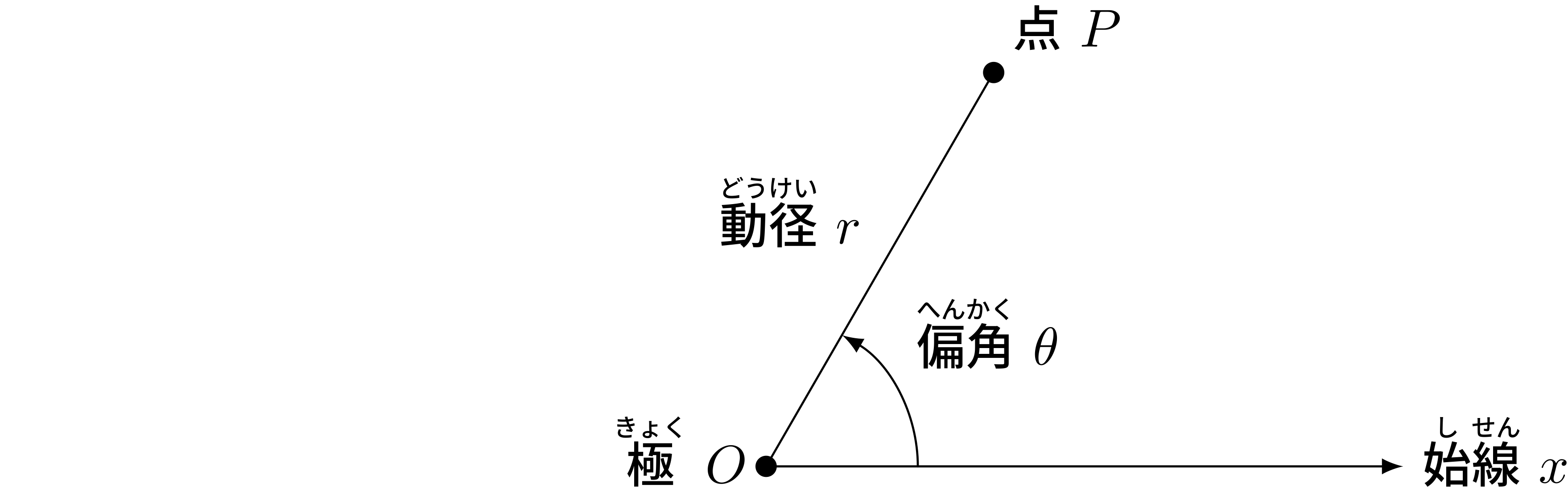
平面上に極と呼ばれる点 $O$ を決めます。
極から伸びる始線という半直線 $x$ を一つ定めます。
平面上の任意の点 $P$ に対して次のように $r$ と $\theta$ を定めます。
そして、動径 $r$ と偏角 $\theta$ の組、
$$ (r, \theta) $$ で点 $P$ を表すことにします。
ユーリ「んー……極座標って、これだけの話? 点を表すのに距離と角度を使うってこと?」
僕「そうだね。点を表すのに動径と偏角の組を使う。極座標の基本的アイディアはそれだけの話。わかった?」
ユーリ「わかった。何も難しくない」
僕「それはよかった。……いまのが極座標の話。 僕たちがふだん使っているのは極座標じゃなくて直交座標だね。 直交座標の基本的アイディアはユーリも知ってると思うけど、こういうもの」
直交座標の基本的アイディア
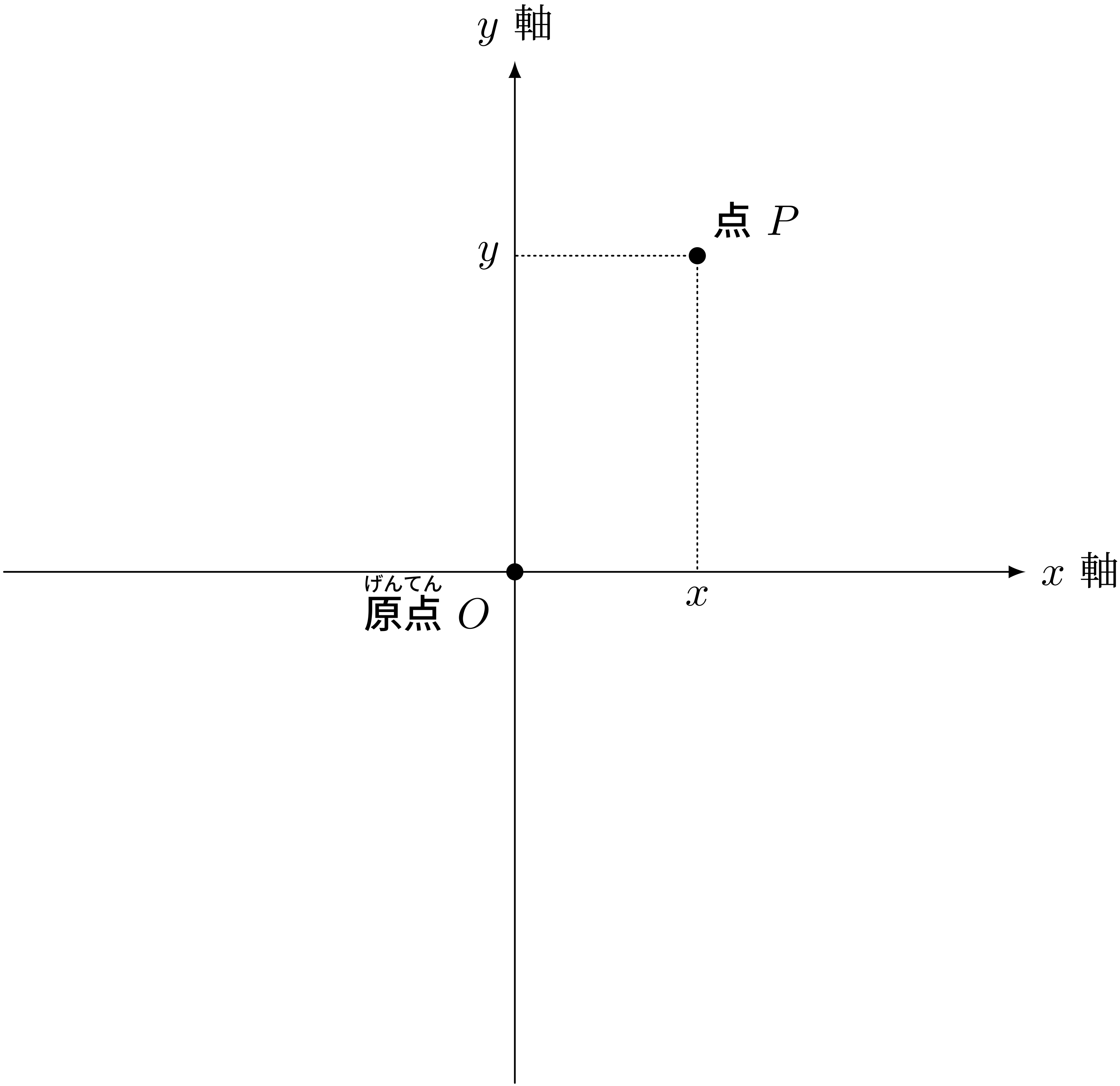
平面上に原点と呼ばれる点 $O$ を決めます。
原点で垂直に交わる $x$ 軸と $y$ 軸という二本の座標軸を決めます。
それぞれの座標軸は原点を $0$ とする数直線になっています。
平面上の任意の点 $P$ を、 $x$ 座標の値と $y$ 座標の値との組、 $$ (x, y) $$ で表すことにします。
ユーリ「うん。これは知ってる」
僕「極座標が $r$ と $\theta$ のペアで点の位置を表して、 直交座標は $x$ と $y$ のペアで点の位置を表す……という話だね、大ざっぱにいうと」
ユーリ「ふーん……そんで?」
僕「極座標と直交座標は、どちらも平面上の点を表す方法だけど、違いがある。 極座標は、ぐるっと回す回転を表すのが得意なんだ。何しろ点を表すところですでに偏角 $\theta$ が出てきてるからね。 それに比べて、直交座標は慣れていてわかりやすいけれど、ぐるっと回す回転を表すのが苦手だね」
ユーリ「ほーほーほー! 得意とか苦手とかあるんだ! ちょっとおもしろくなってきたかも! 極座標はバージョンアップってこと?」
僕「いやいや、そういうことじゃない。 直交座標は回転を表すのが苦手だけど、ぜんぶ駄目ということじゃないからね。 直交座標は、 $x$ 軸や $y$ 軸に水平や垂直な方向に分けるのは得意だ。 逆に、極座標はそういう分け方は苦手。 極座標には、 $x$ 軸や $y$ 軸のような特別な方向がないから」
ユーリ「ふむふむ! なんかわかるー……でも、わかんね」
僕「がく。何がわからない?」
ユーリ「さっきからお兄ちゃんは、点の話をしてるじゃん? 点は、点だよね。 点はわかるの。極座標ってこーゆーことでしょ? $r$ が $1$ で、 $\theta$ が $60$ 度なら、この点」
極座標で表した点の例 $(r, \theta) = (1, 60)$
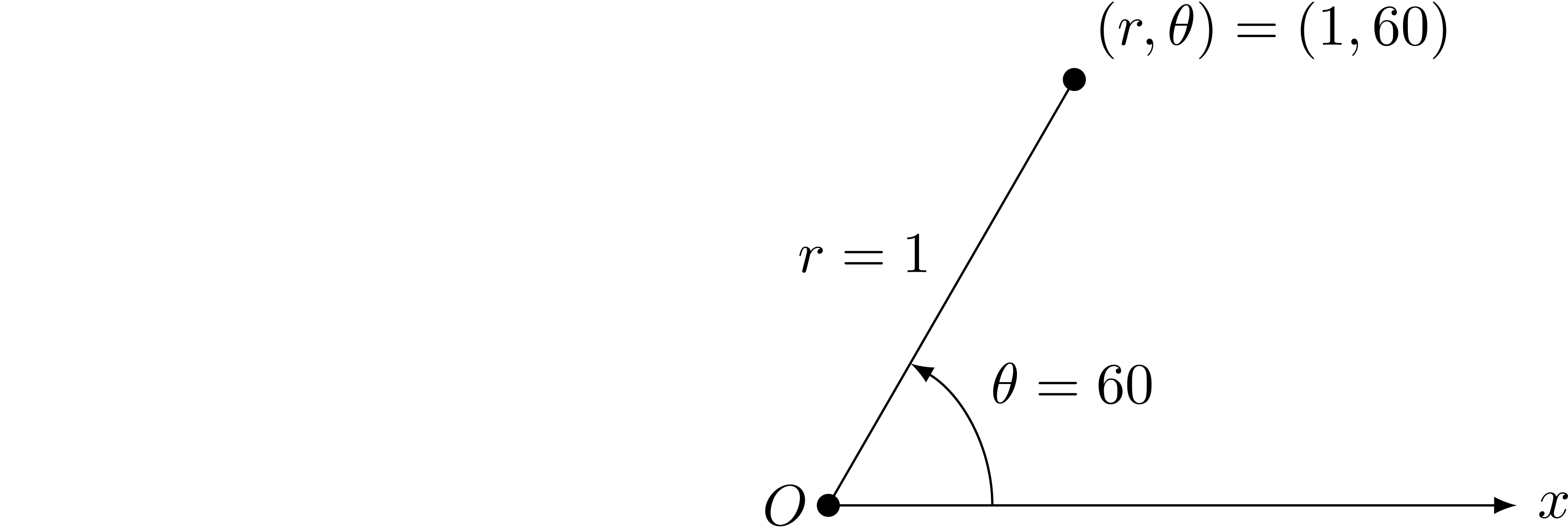
僕「そうだね。偏角はラジアンで考えるのがふつうだけど、いまは度で考えてみようか」
ユーリ「それとか、 $(r, \theta) = (0.5, 270)$ なら、この点になる」
極座標で表した点の例 $(r, \theta) = (0.5, 270)$
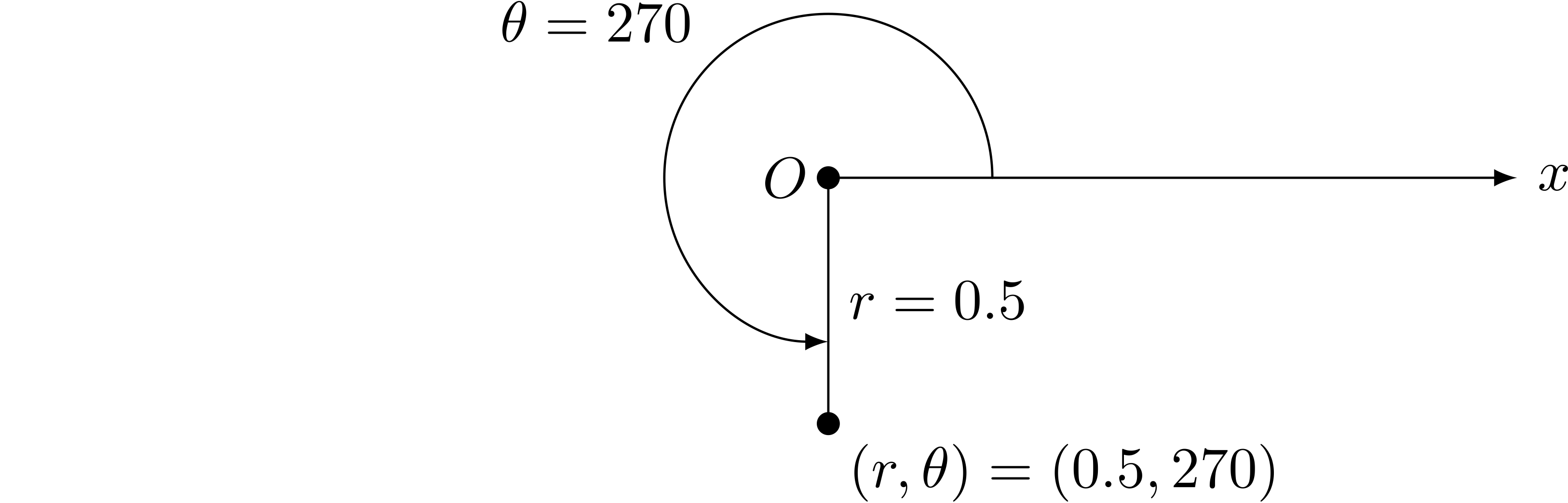
僕「うん、その通り」
ユーリ「でね、でね。点はわかるの。 $r$ と $\theta$ を決めれば点も決まる。そりゃそーだ。 でも、円はどこに出てくるの? コンパスで《ぐるっと回す》ところはどーなってんの?」
僕「ユーリは賢いなあ! そこがおもしろいところだよ! 極座標でひとつの点は $(r,\theta)$ で表せるとしても、 ユーリがいうように、円のようなひとつの図形を極座標で表すにはどうしたらいいかを考えてみよう」
ユーリ「うんうん。わかるよーに頼むぞよ」
僕「そもそも平面に描かれた図形とは、どういうものだと考えればいいか」
ユーリ「図形とは……」
僕「平面に描かれた図形とは、平面上の点の集まりだと考えることにしよう」
ユーリ「うん。それはナットク」
僕「では、平面上の点の集まりをどうやって表せば、図形を表したことになるだろうか」
ユーリ「どーやって表せばいーか? それを聞きたいんですけどー」
僕「こんなふうに考えてみよう。平面上の点をひとつ選んで、
『この点はその図形上にありますか?』
と尋ねる」
ユーリ「おお」
僕「『はい、あります』か『いいえ、ありません』で答えることができるとしたら、その図形を表したことになる」
ユーリ「うっわー……すごーく、まわりくどいこと言ってるみたい」
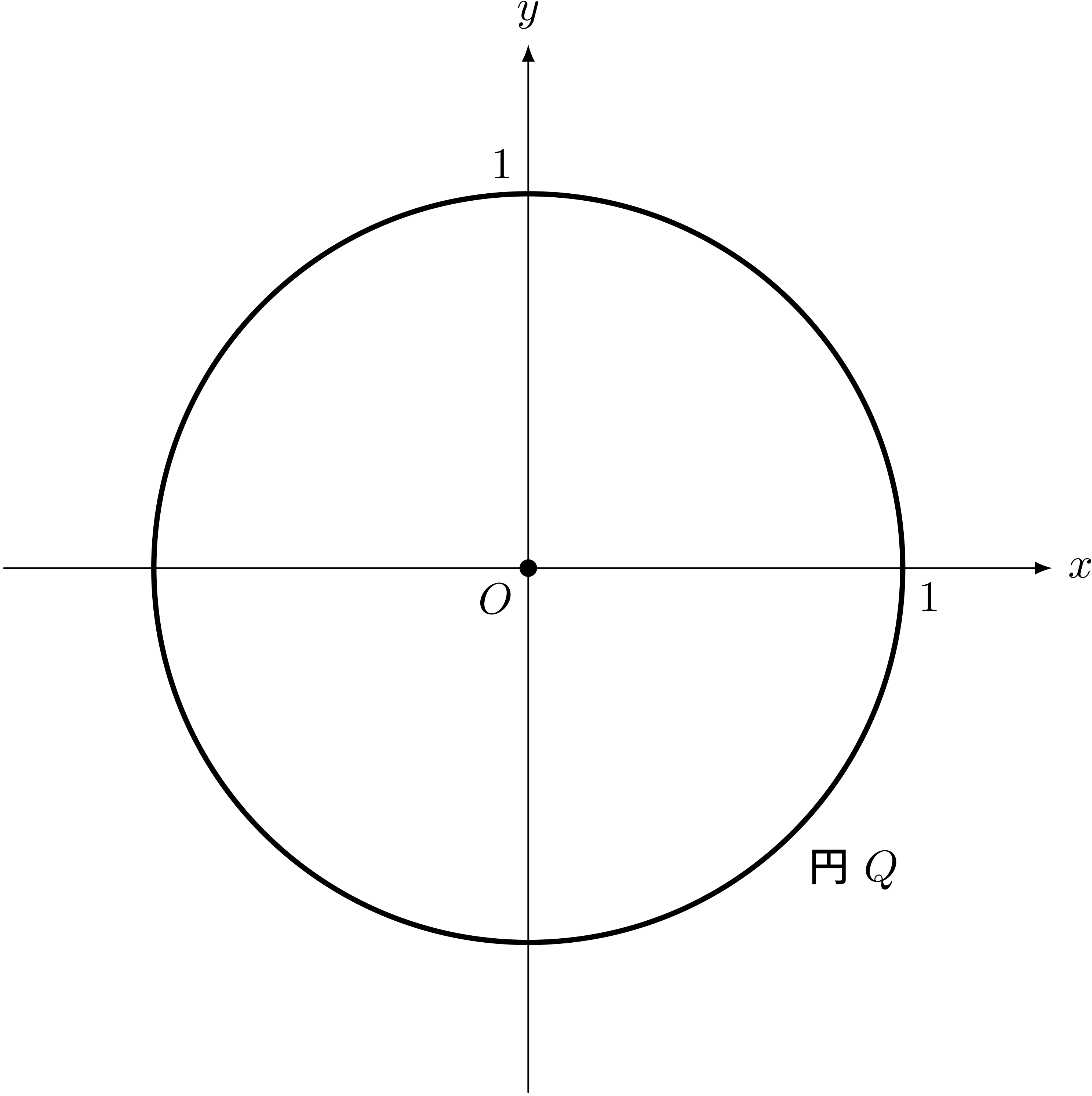
僕「でも意味はわかるよね。たとえば $O$ を中心として半径 $1$ の円を例にしてみようか。 $O$ を中心として半径 $1$ の円、この円周という図形を考える。 この図形を、
円 $Q$
と呼ぶことにしようか」
ユーリ「いいよん」
僕「いつもは円 $O$ みたいに中心の名前をそのまま円にするんだけど、点 $O$ とはっきり分けたいから円 $Q$ としてみよう」
中心 $O$ で半径 $1$ の円に、円 $Q$ と名前を付けた
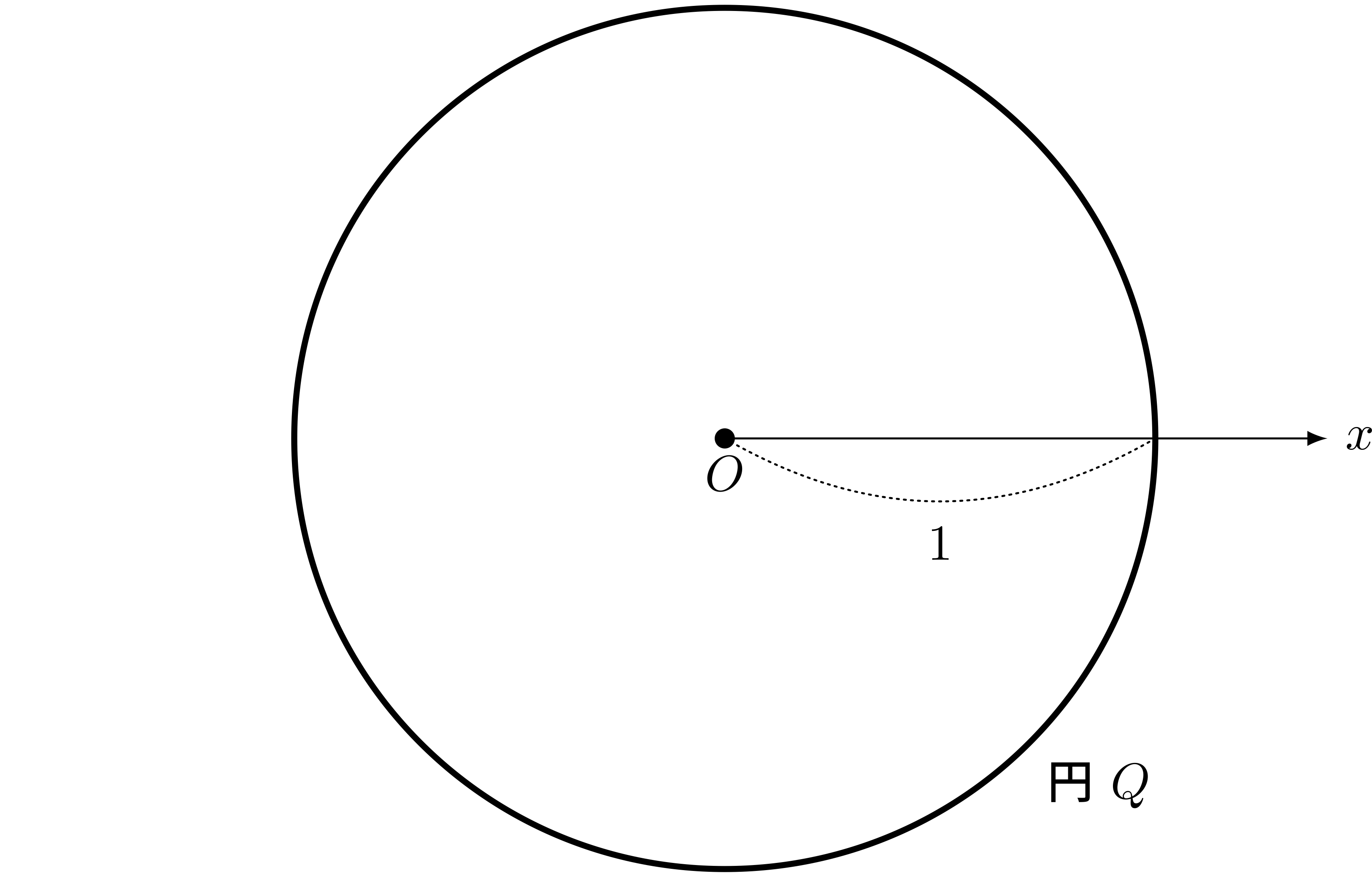
ユーリ「わかるよん」
僕「たとえば極座標で $(r,\theta) = (1, 30)$ という点は、円 $Q$ 上にある?」
ユーリ「もちろん、あるよん」
点 $(r,\theta) = (1, 30)$ は円 $Q$ 上にある
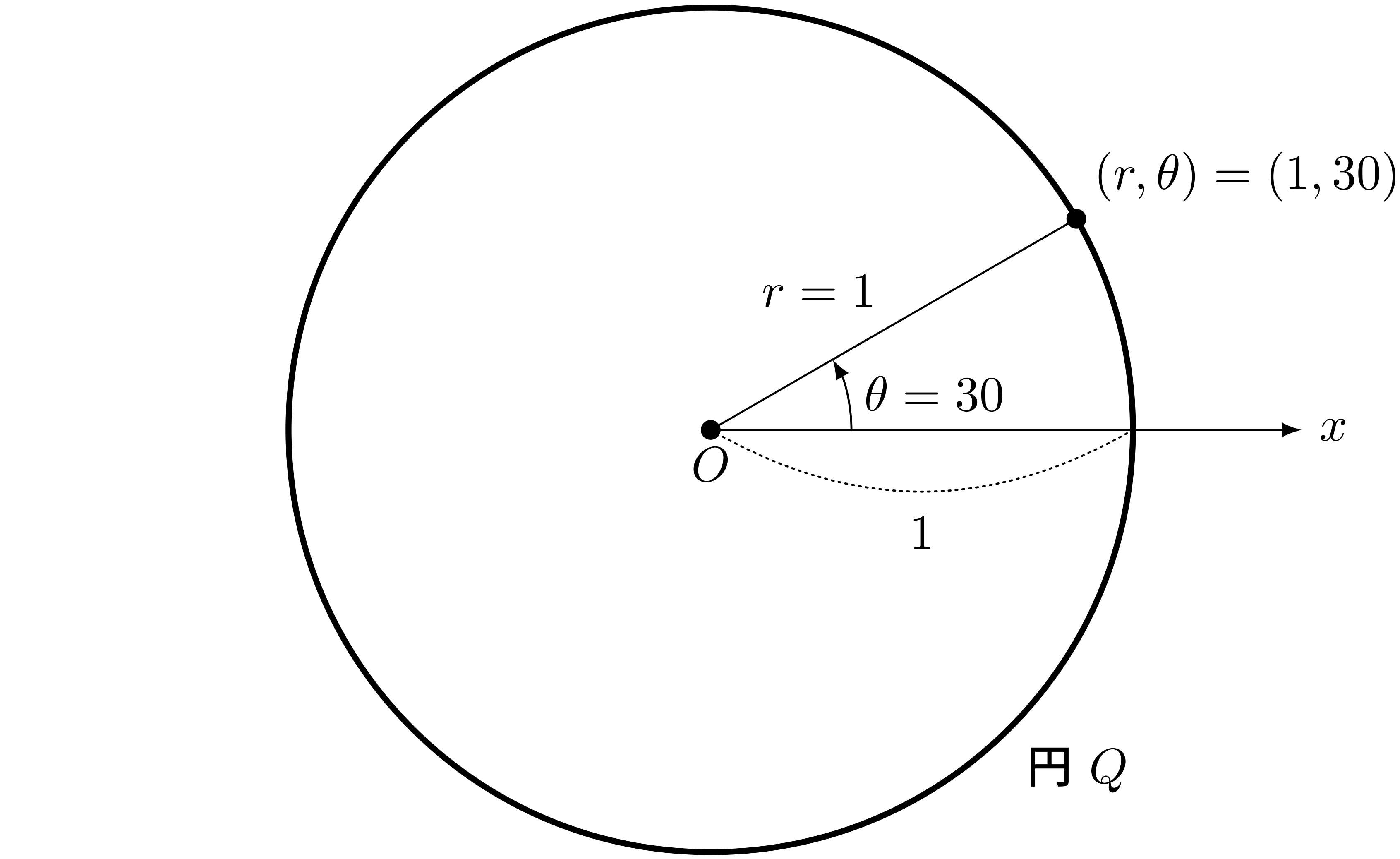
僕「はい、正解!」
ユーリ「簡単じゃ」
僕「今度は、たとえば点 $(r, \theta) = (0.5, 120)$ という点は、円 $Q$ 上にある?」
ユーリ「それって $r = 0.5$ で $\theta = 120$ ってことだよね。だったら、その点は円 $Q$ 上にはない!」
点 $(r,\theta) = (0.5, 120)$ は円 $Q$ 上にはない
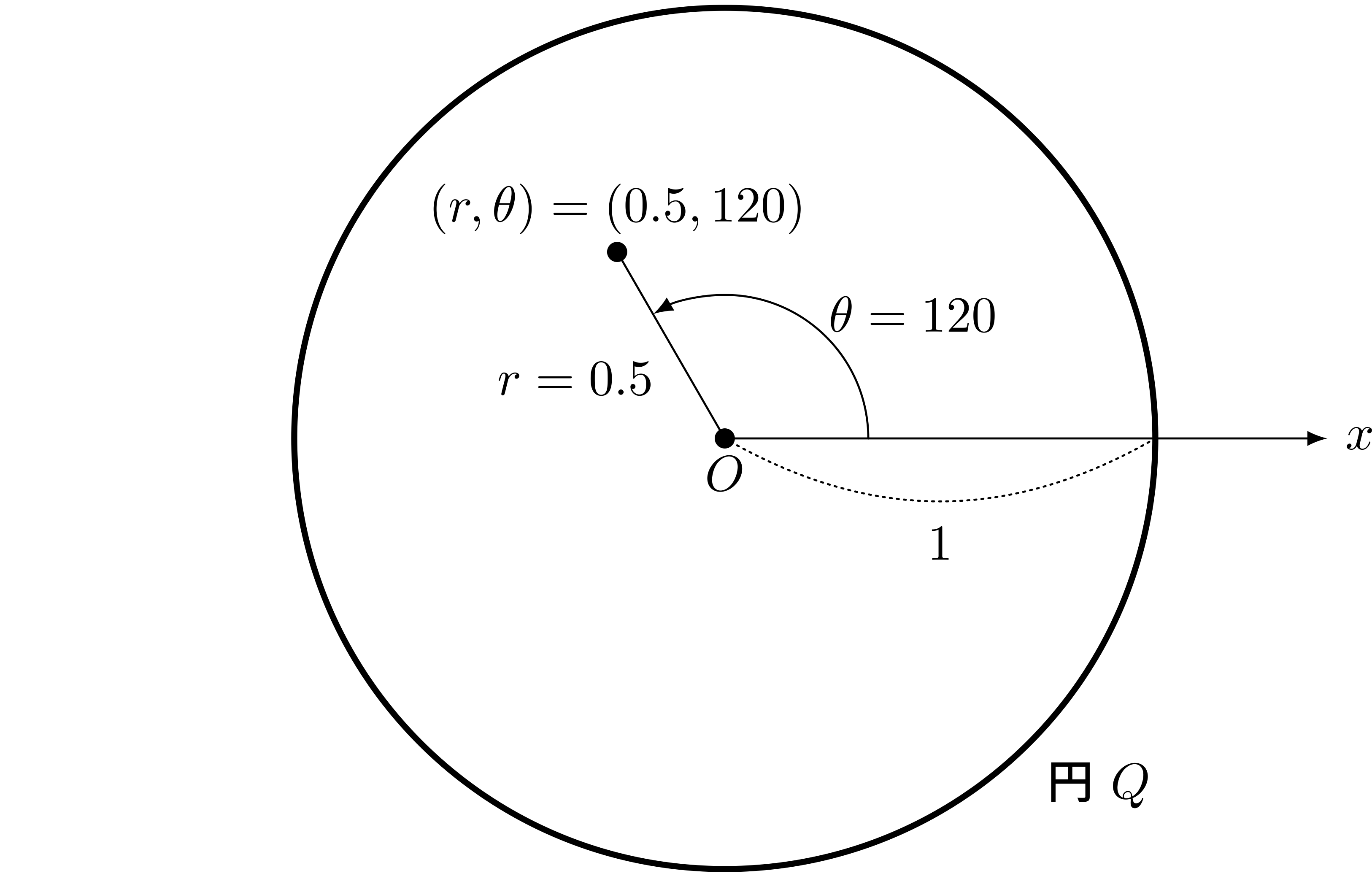
僕「そうだね、正解! 次に……」
ユーリ「ちょっと待ってよ、お兄ちゃん。 そんなことして、一つ一つ調べてもキリがないじゃん。 点は無数にあるんだもん」
僕「そこだよ」
ユーリ「どこだよ」
僕「無数の点と戦うためには知恵がいる」
ユーリ「バトルが始まるんかい」
僕「点は無数にある。だから、一つ一つ『この点はその図形上にありますか?』と尋ねることはできない。 ユーリが言う通り、キリがないから。 でも、図形は点の集まりで、図形がどんなものかをきちんというためには、 『この点はその図形上にありますか?』に答えられなくちゃ困る。さてどうするか」
ユーリ「どーするかっつってもなー……困ってるのはユーリだよ」
僕「そこで、数式が登場する」
ユーリ「何かと言えば数式を持ち出す《数式マニア》は健在だにゃあ!」
僕「数式を使って図形を表す。それはとても大事なことなんだ。 《数式》といってもいいし、ただの《式》といってもいいし、《条件式》といってもいい。 ともかく、与えられた点がその図形上にあるかどうかを表した数式を手に入れたい。 なぜなら、その数式があれば『この点はその図形上にありますか?』に答えられるから」
ユーリ「ふーん……そっか。お兄ちゃんが言いたいこと、わかってきた。 点を一つ一つ調べてたらキリがないけど、数式をどどーんと置いとけばいいじゃん!……ってこと?」
僕「そういうこと。直線を表す数式、円を表す数式、楕円を表す数式……とにかく、目的の図形を表す数式を用意する」
ユーリ「どどーんと」
僕「図形を表す数式を、どどーんと用意する。その数式には文字が含まれていて……」
ユーリ「わかるわかる。 $x$ とか $y$ とか、点を表すための文字でしょ? $r$ とか $\theta$ とか」
僕「そうだね。 図形を表す数式には点を表す文字が含まれている。あとは具体的な点を当てはめてやって、 その数式が成り立つかどうかを調べればいいというわけだ。 だから、《数式を使って図形を表す》というのは、無数の点を取り扱うためのすごく強い武器になるわけだね。 数式は無限と戦う武器になる」
ユーリ「おおっ! お兄ちゃん、心の俳句」
数 式 は 無 限 と 戦 う 武 器 に な る
僕「そういうこと」
ユーリ「うん、数式が大事なのはわかったよ、お兄ちゃん。 でも、極座標で円を表すって、結局どーすんの? 具体的に」
僕「極座標で考えたとき、極となっている点 $O$ を中心として、半径 $1$ の円 $Q$ を表す数式は、 $$ r = 1 $$ になるよ」
ユーリ「は?」
僕「だから $r = 1$ が、円 $Q$ を表す数式になる。これを極座標を使った円 $Q$ の方程式と呼ぶこともある。 もっと短く円 $Q$ の極方程式ということもある」
円 $Q$ の極方程式 $r = 1$

ユーリ「$r = 1$ だけ? 何だかおかしくない?」
僕「何がおかしいんだろう」
ユーリ「カンタンすぎるから。 $r = 1$ で円を表すわけ?」
僕「そうだよ。さっきの話を思い出して。『この点はその図形上にありますか?』と尋ねられたときに、 数式があると答えられるといったよね」
ユーリ「……」
僕「そして実際、 $r = 1$ という簡単な式だけで、円 $Q$ の上にあるかどうかを判定できる」
ユーリ「……ねえ、 $r = 1$ という式は、動径 $r$ が $1$ だってことだよね?」
僕「そうだよ。 $r = 1$ という式は『極からその点までの距離が $1$ である』ことを表している。 そして『その点が円 $Q$ であることの条件』はまさにそれなんだ」
ユーリ「……」
僕「極座標では、平面上の一点を動径 $r$ と偏角 $\theta$ の組で表す。つまり、 $$ (r, \theta) $$ という二つの数の組が一点を表す。だから極座標で円を表す数式には $r$ や $\theta$ が出てくる」
ユーリ「そこ!」
僕「どこ?」
ユーリ「あのね、 $r = 1$ が円 $Q$ の半径が $1$ だからなのは、わかる。 でもね、 $r = 1$ って式には $\theta$ が出てきてないじゃん。それでもいーの?」
僕「ユーリは素晴らしいな! 式を読んで、ちゃんと考えてる」
ユーリ「だって、考えなくちゃわかんないじゃん」
僕「円 $Q$ の極方程式 $r = 1$ には、偏角を表す $\theta$ が出てきていない。それでもいいんだよ」
ユーリ「なんで?」
僕「なぜかというと、与えられた点 $(r, \theta)$ が円 $Q$ という図形上にあるかどうかは、 動径 $r$ さえ調べればいいから。偏角 $\theta$ がどんな値であっても構わない。 偏角 $\theta$ がどんな値であっても、その点が円 $Q$ という図形上にあるかどうかには影響しない。まったく影響しない。 動径 $r$ の大きさが $1$ かどうか。そこが勝負どころになる。だから、円 $Q$ の極方程式には $\theta$ が出てこないんだよ」
ユーリ「ははーん……」
僕「極座標で、点は $(r, \theta)$ という二つの数の組で指定される。そして……」
ユーリ「ユーリ、百パーセント理解した! わかった、わかりましたぜ、ダンナ」
僕「誰がダンナだよ」
ユーリ「$r = 1$ を調べるだけで、円 $Q$ 上にあるかどうかがわかる。だから、 $r = 1$ が円 $Q$ の……なんだっけ」
僕「円 $Q$ の極方程式」
ユーリ「きょくほうていしき! だから、 $r = 1$ が円 $Q$ の極方程式になる。ユーリ、百パーセント理解したよん」
僕「いいぞ、いいぞ! さあここで、話を戻そう」
ユーリ「どこに?」
僕「極座標は回転を表すのが得意で、直交座標は苦手という話に」
ユーリ「ほほー」
僕「極座標で考えるとき、円 $Q$ の極方程式は $r = 1$ のように簡単になる。 でも、直交座標で考えるとき、同じ円 $Q$ の方程式は $x^2 + y^2 = 1$ になる。それほど難しいわけじゃないけれど、 $r = 1$ に比べたらずいぶん複雑だよね」
ユーリ「おおー、確かに!」
円 $Q$ の極方程式 $r = 1$(極座標)

円 $Q$ の方程式 $x^2 + y^2 = 1$(直交座標)
僕「直交座標では点を $(x, y)$ という二つの数の組で表す。二つの数の組で表すことは極座標と同じだけど、 数が表しているものの意味は違う。 $x,y$ はそれぞれ $x$ 座標の値と、 $y$ 座標の値になる」
ユーリ「ふんふん」
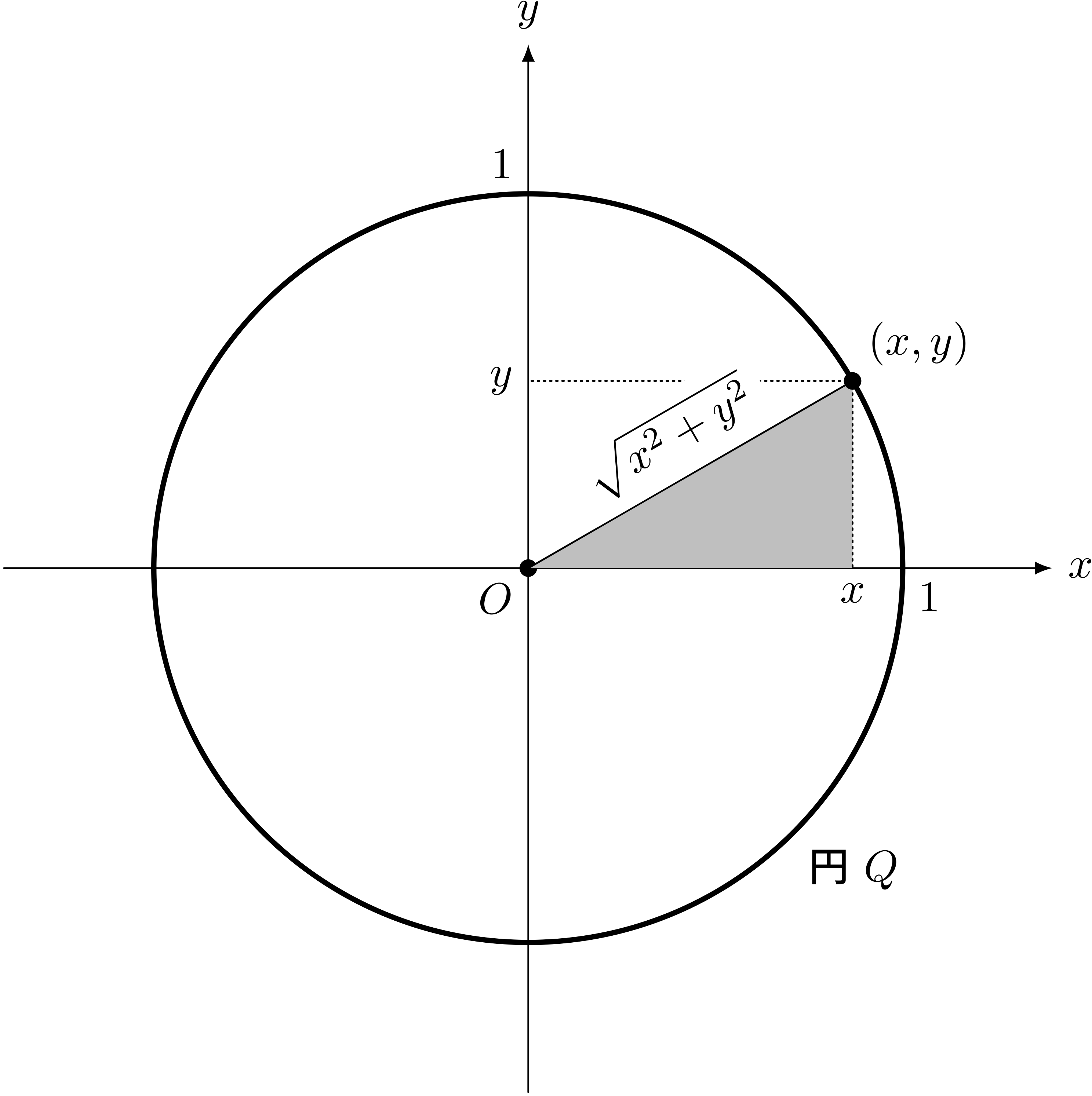
僕「そして $x^2 + y^2 = 1$ というのは『原点 $O$ と点 $(x,y)$ の距離が $1$ である』ことを表している式だといえる」
ユーリ「うん、それはお兄ちゃんがよく教えてくれるから知ってる。三平方の定理でしょ?」
僕「そうそう。三辺の長さが $a,b,c$ である直角三角形で、 斜辺の長さが $c$ とすると、 $$ a^2 + b^2 = c^2 $$ が成り立つ。つまり、斜辺の長さは、 $$ c = \SQRT{a^2 + b^2} $$ で得られる。 だから、直交座標にある点の座標を $(x,y)$ とすると、原点との距離は、 $$ \SQRT{x^2 + y^2} $$ で得られることになる」
$x^2 + y^2 = 1$ は、原点 $O$ との距離が $1$ であることを表している
僕「だから、円 $Q$ の極方程式 $r = 1$ と、円 $Q$ の方程式 $x^2 + y^2 = 1$ は同じことをいってることがわかるね」
ユーリ「あー、そだね。どっちも点 $O$ からの距離が $1$ ってことだから」
僕「極座標ではもともと動径 $r$ が点 $O$ からの距離を表しているので、円 $Q$ の極方程式は簡単に書ける。 でも直交座標では、点 $O$ からの距離を表すために $x$ と $y$ とを組み合わせた式を作る必要がある。 $x^2 + y^2 = 1$ という式を成り立たせるためには、 $x$ と $y$ が《ちょうどいい感じ》にバランスを取る必要があるわけだ」
ユーリ「ちょうどいい感じ?」
僕「$x$ が大きいときには、 $x^2 + y^2 = 1$ を満たすために、 ちょうどいい感じに $y$ が小さくなっている必要があるって意味。 それがどういうふうに《ちょうどいい》のかをきちんと表しているのが $x^2 + y^2 = 1$ という式だし、 その結果得られたのが半径 $1$ の円 $Q$ ということになる」
ユーリ「円じゃない別の形だったら、別の《ちょうどいい感じ》になるってこと?」
僕「そうだね。極座標で表した場合でも、直交座標で表した場合でも、 点の座標を表す文字を含んだ式を使って図形を表すことができる。 図形を表す数式は、
『この図形は、この式をちょうど成り立たせるような点の集まりですよ!』
ということを主張しているんだね」
ユーリ「ふむふむふむふむ! ねえお兄ちゃん! 極座標で他の図形も表してみたい!」
僕「なるほど。じゃあね、こんな問題はどう? これは以前、ミルカさんがテトラちゃんに出した問題だよ」
問題(極方程式)
次の極方程式が表すのはどんな図形か。
$$ r = \theta $$
※偏角 $\theta$ は「度」で表しているとします。
ユーリ「お、おおお?」
ユーリ「ところでお兄ちゃん、何で《極座標の定義》じゃなくて《極座標の基本的アイディア》なの? 何か足りないの?」
僕「それは次回のお楽しみに!」
ユーリ「おーい、引っ張るなー!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第361回終わり)
(2022年7月15日)