![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)
結城浩です。いつも「数学ガール」の応援ありがとうございます。
2022年のcakesサービス終了にともない、 Web連載「数学ガールの秘密ノート」の引っ越しが行われました。 ちょうどよい機会なので、登場人物たちにそれまでの振り返りをしてもらいます。
第359回では「第1回から第180回まで」を振り返り、 第360回では「第181回から第358回まで」を振り返ります。
彼女たちの振り返りを聞いていると、 ずいぶんいろんな話題を話してきたんだなあ……と思います。
それではお楽しみください。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
僕「ええと、ということで、今回と次回はおしゃべりしながらこれまでを振り返りましょうになったみたいだよ」
ユーリ「でもね、お兄ちゃん。360回分、全部振り返ったらすごい数になっちゃうし、一年くらい掛かるんじゃね?」
僕「いや、各シーズン単位でまとめていけばいいんじゃないかな」
ユーリ「シーズン?」
ミルカ「10回単位」
僕「10回ごとに思い出深い話題や、印象に残った問題を挙げていくことにしようか」
テトラ「それにしても第1回〜第360回でちょうど360回分あるというのは、まるでぐるっと一回りするみたいですね。360度、ぐるっと」
僕「第1回〜第10回の「式とグラフ」シーズンでは、式とグラフのおしゃべりをしたね。連立方程式の話をしたり、比例と反比例の話をしたり、二次関数の話をしたり」
テトラ「なんと言っても、 $$ (a + b)(a - b) = a^2 - b^2 $$ という恒等式がおもしろかったですっ! その図形的解釈ですね(第2回参照)。これです」
$(a + b)(a - b) = a^2 - b^2$ の図形的解釈
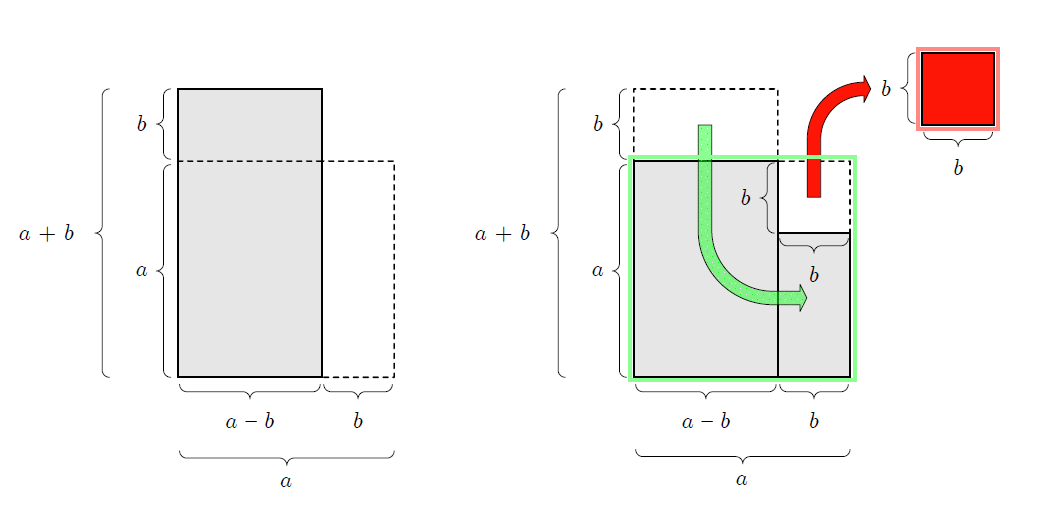
ユーリ「えーと……左が長方形の面積 $(a + b)(a - b)$ で、 右が正方形の面積 $a^2$ から、小さな正方形の面積 $b^2$ を引いたもの。 たーのしー!」
ミルカ「式を図形で解釈する。図形を式で表現する。どちらも楽しい」
僕「《二つの世界》をつなぐからだね」
僕「第11回〜第20回は「整数で遊ぼう」のシーズン。 謎のパズルで遊んだり、数当てゲームをしたり。いろいろやったね。フィボナッチ数列も出てきた」
ユーリ「やっぱ、ここではぐるぐるワンの時計パズルでしょーな(第19回参照)」
僕「カウントボタンを押すと針が進む三つの時計を使ったパズルだね。 ただし、2回でひとまわり、3回でひとまわり、5回でひとまわりするという特殊な時計」
ぐるぐるワンの時計パズル(初期状態0,0,0)
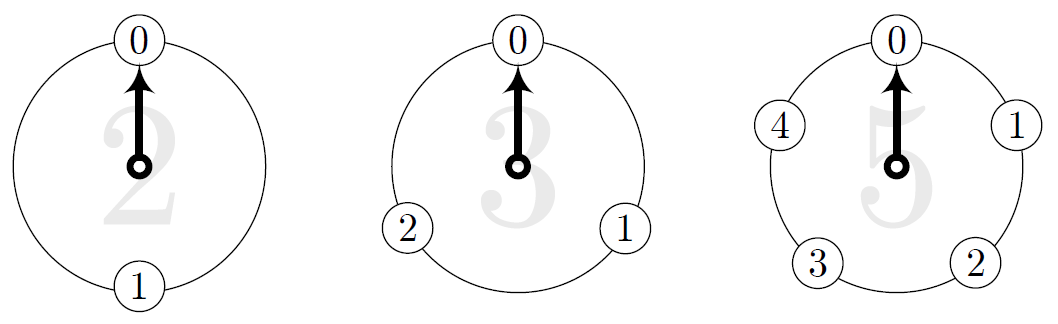
ぐるぐるワンの時計パズル(カウントボタンを2回押した状態0,2,2)
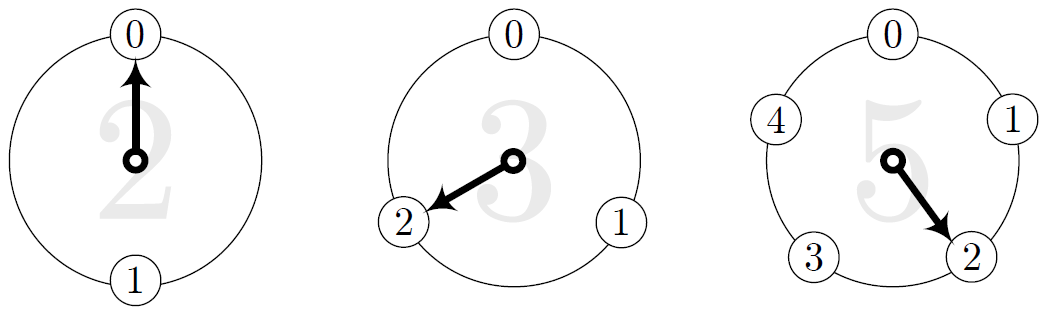
テトラ「これは……パズルなんですか?」
ユーリ「そだよん。状態0,0,0からカウントボタンを何回押せば状態0,2,4になるかにゃ?」
テトラ「なるほど。根気よく考えればわかりますけど……」
ミルカ「三つの時計が一つの時計になるわけだな」
ユーリ「あっ、ミルカさま、ヒントだめ! ……って、いまのがヒント?」
ミルカ「第21回〜第30回は「丸い三角関数」のシーズン。 $\sin, \cos$ の定義から加法定理まで」
ユーリ「ユーリは、お兄ちゃんと円周率を数えたよ!」
テトラ「円周率を……数える? どういうことですか、ユーリちゃん」
ユーリ「方眼紙に円を描いて……こんな感じ!」
方眼紙に円を描く
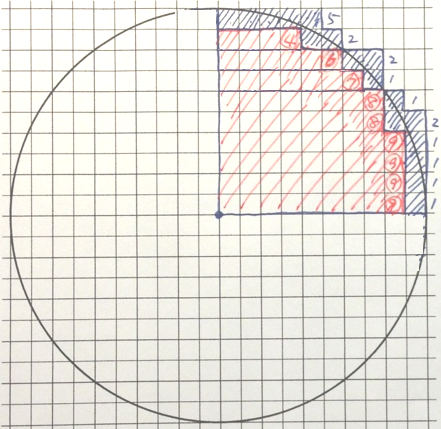
テトラ「ああ……マス目を数えるということですね」
ユーリ「内側と外側を数えたんだよ!」
僕「半径 $r$ の円を描いて、《円の内側にすっぽり入る正方形の個数》と《円を包み込むための正方形の個数》を数える。 そうすると、その間に《円の面積 $S$》がはさまれるはずだよね。 すると、 $$ S = \pi r^2 $$ の式を使えば、円周率 $\pi$ の値がどのくらいになるか、はさみうちでわかる」
テトラ「おもしろそうですね……これで $3.14$ が求められるなんてすごいですっ!」
ユーリ「……」
僕「……」
テトラ「えっえっ? 違うんですか?」
ユーリ「えへへ……(第27回参照)」
僕「そうはうまくいかなかったよね」
ユーリ「でも、あとからアルキメデスの方法で、 $3.14$ までは行ったよ!(第28回参照)」
ミルカ「第31回〜第40回は「数列の広場」のシーズン」
ユーリ「確か、お兄ちゃんがオセロでボロ負けしたシーズン(第31回参照)」
僕「そういう話よりも、数列の階差数列を調べた話を思い出そうよ(第32回参照)」
平方数の階差数列
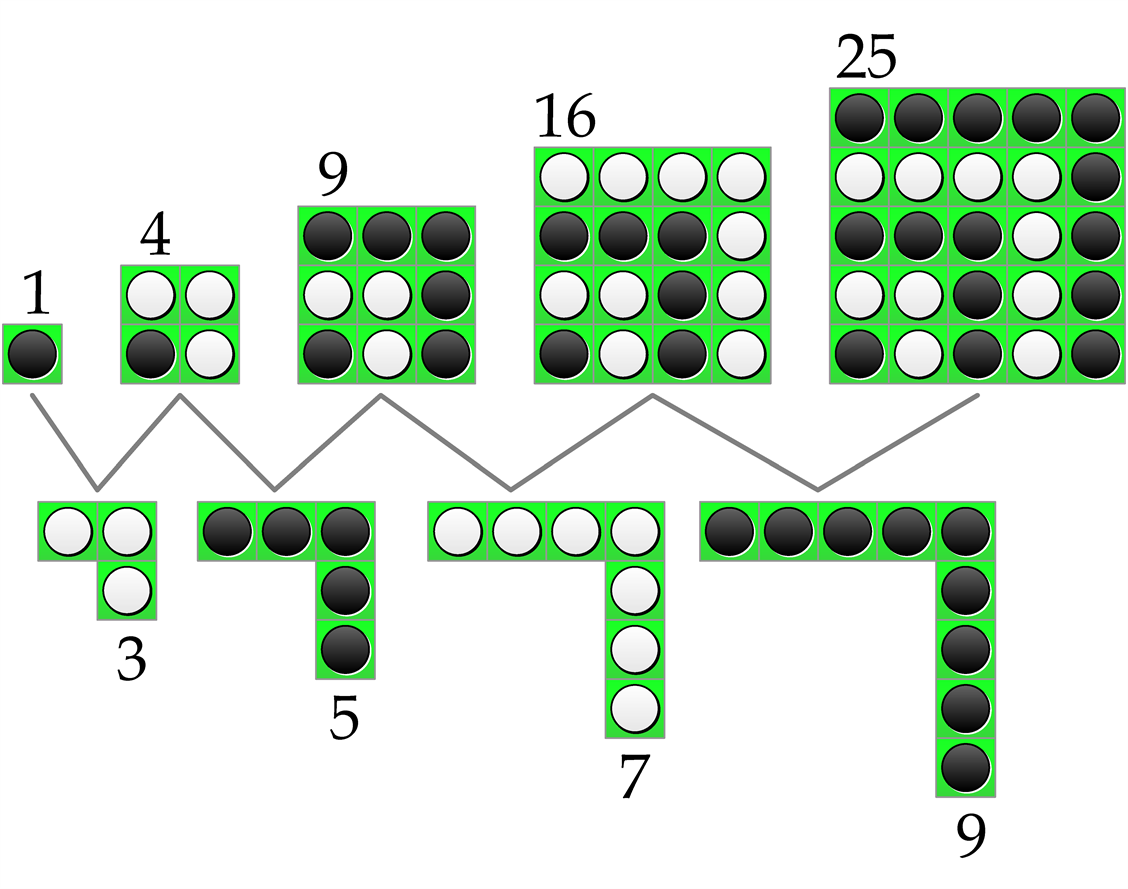
テトラ「あたしは何と言っても、$$\sum$$の使い方を学んだのが大きかったです。 意味がわかればこわくなくなりました(第33回参照)」
僕「テトラちゃんは、 $$ \sum_{k = 1}^{n} f_k(x) $$ という数式が難しいという話を持ってきたね」
ユーリ「難しくないの? この $f_k(x)$ って何?」
僕「もちろん、この式が何を表しているかは説明がないとわからないけど、 この式そのものは、 $$ f_1(x) + f_2(x) + \cdots + f_n(x) $$ といってるだけなんだ」
ミルカ「和だ」
僕「第41回〜第50回は「微分を追いかけて」のシーズン。これはユーリの無茶ぶりがすごかった」
ユーリ「何だっけ?」
僕「『微分をちゃちゃっと教えろ!』と命令してきたよね(第43回参照)」
ユーリ「でも、お兄ちゃん、ちゃんと教えてくれたじゃん。無茶じゃないね」
テトラ「グラフを使ったんですよね」
僕「そうそう。《位置のグラフ》から《速度のグラフ》を得るのは、時刻で微分することだから。 直線上を等速度で移動している点Pの位置をpとして、速度をvとすると、こうなる」
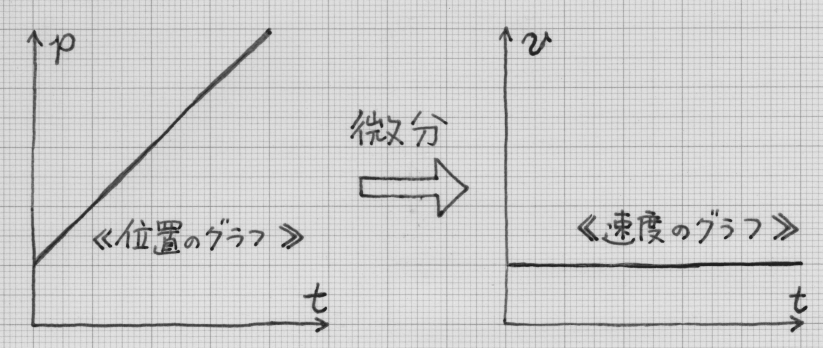
ユーリ「第51回〜第60回は「ベクトルの真実」のシーズンだったよ。 ベクトル真実(まみ)ちゃんって、誰? 新キャラ?」
僕「真実(まみ)じゃなくて、真実(しんじつ)」
テトラ「このシーズンで一番感動したのはこの問題でした(第57回参照)」
問題
円 $x^2 + y^2 = 1$ 上の点 $(a, b)$ で、 この円に接する直線の方程式を求めよ。
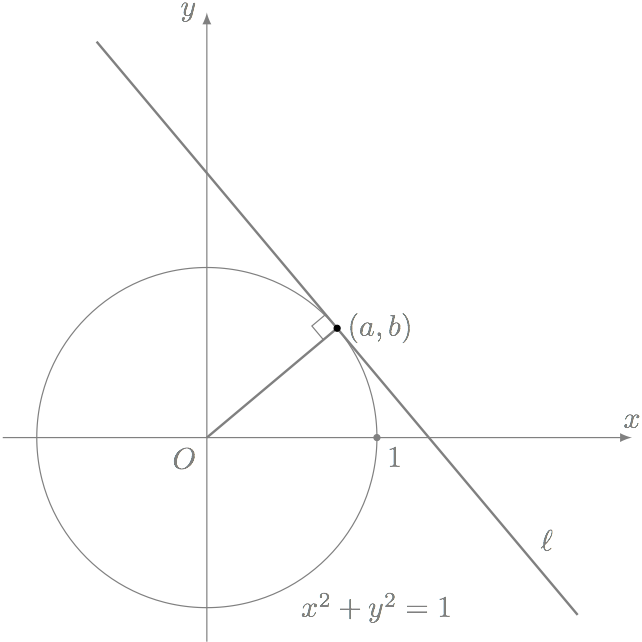
僕「内積で考えたんだっけ」
テトラ「そうです、そうです」
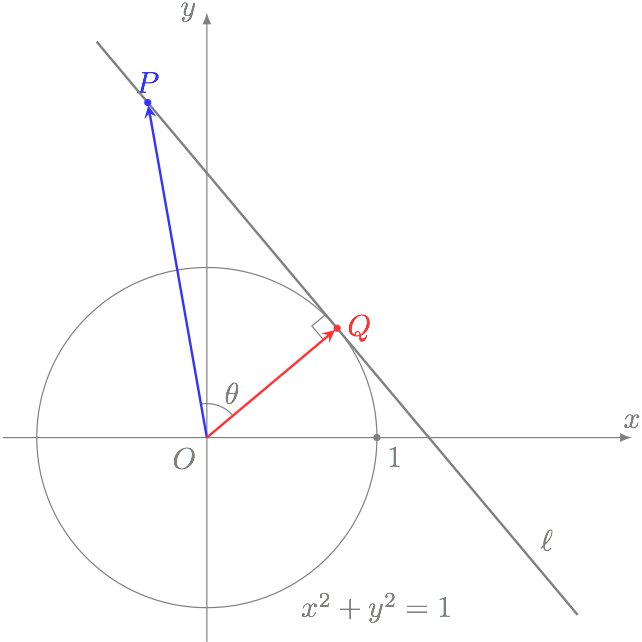
僕「ベクトルの内積は慣れないとまったくわからないけど、慣れてくるといろんなものが内積に見えてくるよね」
ミルカ「第61回〜第70回は「場合の数」のシーズンか。何を話したかな」
僕「順列と組み合わせだね。円順列、数珠順列……」
ユーリ「集合のヴェン図もやったよ。時計の文字盤を使った、こんなクイズ(第63回参照)」
クイズ(どんな数の集合?)
$\SET{2,3,4,8,9,10}$ って、どんな数の集合?
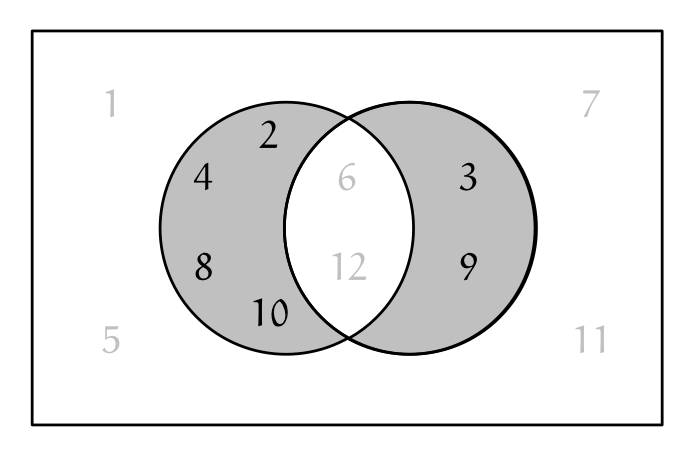
テトラ「どんな数の集合って、どう答えればいいんですか?」
僕「2の倍数と3の倍数を使って答えるクイズだっけ?」
ユーリ「そーそー! (《2の倍数である》かつ《3の倍数でない》数)または(《2の倍数でない》かつ《3の倍数である》数)の集合!」
ユーリ「第71回〜第80回は「指数と対数」のシーズンで、 ものすごーく大きな数が出てきたんだよね。テトレーション」
テトラ「あ、あたしですか?」
ユーリ「テトラさんじゃなくて、テトレーションだよん(第72回参照)」
僕「加算を繰り返すのが乗算。乗算を繰り返すのが冪乗。そして冪乗を繰り返すのがテトレーション。 ギリシア語の接頭辞はモノ(1)→ジ(2)→トリ(3)→テトラ(4)という順番で、 冪乗の次という意味でテトレーションという名前になったんだね。 加算→乗算→冪乗→テトレーションという順番で 4 番目」
冪乗(exponentiation)は乗算の繰り返し
$$ a^{n} = \underbrace{a \times a \times a \times \cdots \times a}_{\REMTEXT{$n$個の$a$}} $$
テトレーション(tetration)は冪乗の繰り返し
$$ {}^na = \underbrace{a^{a^{a^{\cdot^{\cdot^{\cdot^{a}}}}}}}_{\REMTEXT{$n$個の$a$}} $$
テトラ「不思議な書き方ですねえ」
僕「${}^{5}{2}$ を計算したら、すさまじい大きさの数になったよ。まず……」
$$ 115792089237316195423570985008687907853269984665640564039457584007913129639936 $$テトラ「す、すごいですね」
僕「……というこの数の、256乗になるんだ!」
$$ {}^{5}{2} = 115792089237316195423570985008687907853269984665640564039457584007913129639936^{256} $$テトラ「!!!!」
テトラ「第81回〜第90回は「踊る曲線」のシーズンで、 いろんな曲線についておしゃべりしました」
僕「印象的だったのは、テトラちゃんの雪かなあ」
テトラ「わ、忘れてくださいっ!」
ユーリ「雪って何?」
テトラ「Koch Snowflake……《コッホ雪片》ですけど、手描きに挑戦したんですが、うまくいかなくてですね(第85回参照)」
テトラちゃんの描いた《コッホ雪片》

僕「いや、これは難しいよ」
ユーリ「お兄ちゃんも描いたの?」
「僕」の描いた《コッホ雪片》
ユーリ「これ、どーゆー図形なの?」
ミルカ「コッホ雪片の例はこれ」
《コッホ雪片》の例

テトラちゃんからの挑戦状
きっと読者さんの中には《コッホ雪片ぐらいきれいに描けるよ》と思っている方がいらっしゃるかもしれませんが、 ほんとうに意外と難しいんですよ。
お手本なし、下書きなし、フリーハンドの一筆書きで、 ある程度のレベルの《コッホ雪片》を描いてみてくださいね。
大きな正三角形や正六角形でアタリをつけたりしちゃだめですよっ!
テトラ「たくさんの方が描いてくれました! ありがとうございますっ!」
僕「第91回〜第100回は「不等式」のシーズン。いろんな不等式の証明をしたり、 数の大小関係を調べたり、領域を描いたり……」
ユーリ「お兄ちゃんがムキになって出してきたクイズがこちら(第92回参照)」
クイズ
$a,b,c,d$ を実数とする。
もしも、 $$ a > b > c > d $$ とするとき、以下の $A,B,C$ の大小関係について何がいえるか。 $$ \left\{\begin{array}{llll} A &= ab + cd \\ B &= ac + bd \\ C &= ad + bc \\ \end{array}\right. $$
テトラ「『何がいえるか』というのは $A,B,C$ の大小関係を答えるということでしょうか」
僕「そうだね」
テトラ「これは、根気よく調べれば!」
ミルカ「第101回〜第110回は「ビットとバイナリー」のシーズン。ビット列と二進法表記、それからラティスの話もあった」
テトラ「リサちゃん、お待たせしました!」
リサ「《ちゃん》は不要」
登場人物紹介(追加)
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
ユーリ「このシーズン、リサ姉は何がおもしろかった?」
リサ「変幻ピクセル(第103回参照)」
スキャナとプリンタ

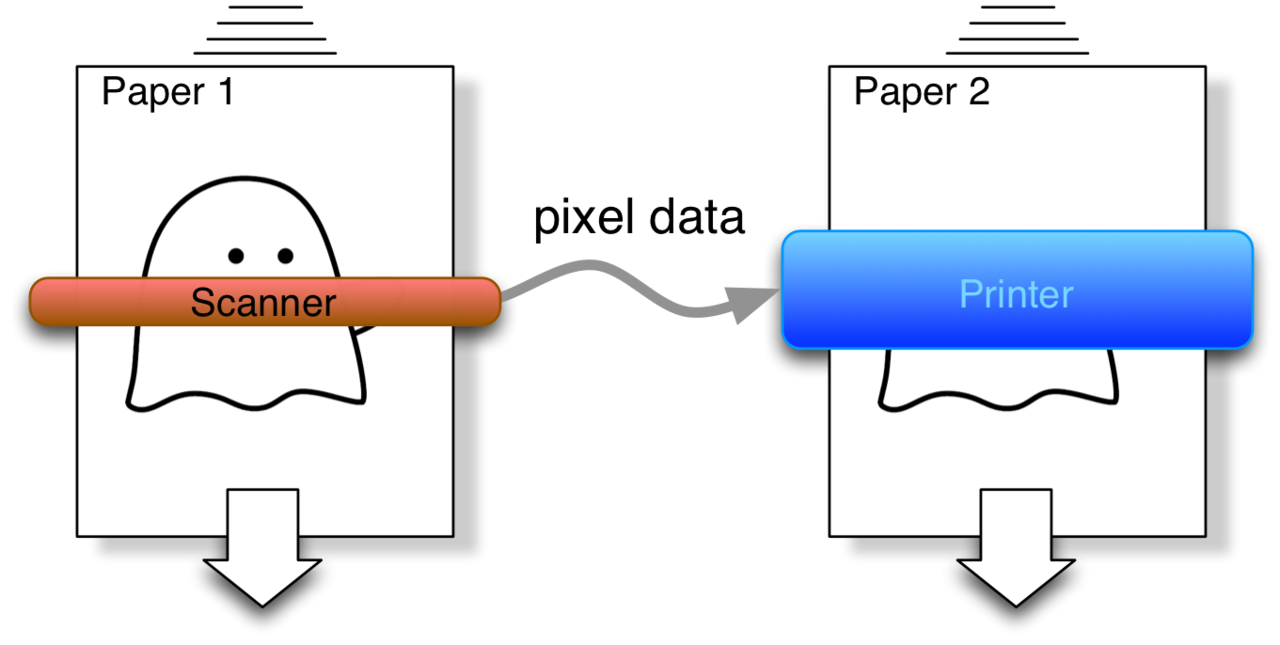
ユーリ「ユーリもユーリも! ビット演算で図形をいじるの楽しかった!」
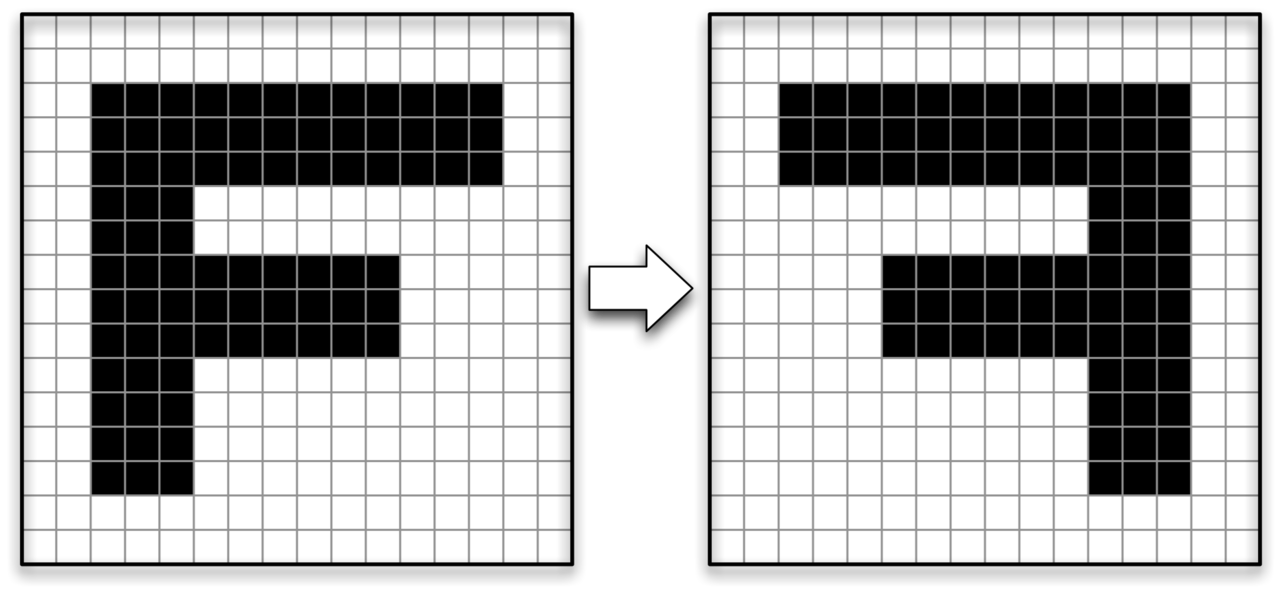
リサ「第111回〜第120回は、「行列が描くもの」のシーズン(咳)」
ミルカ「リサがたくさん図形を描いてくれた(第117回参照)」
リサ「要求過多」
ミルカ「しかし応えるリサ」
座標平面上に描いた点
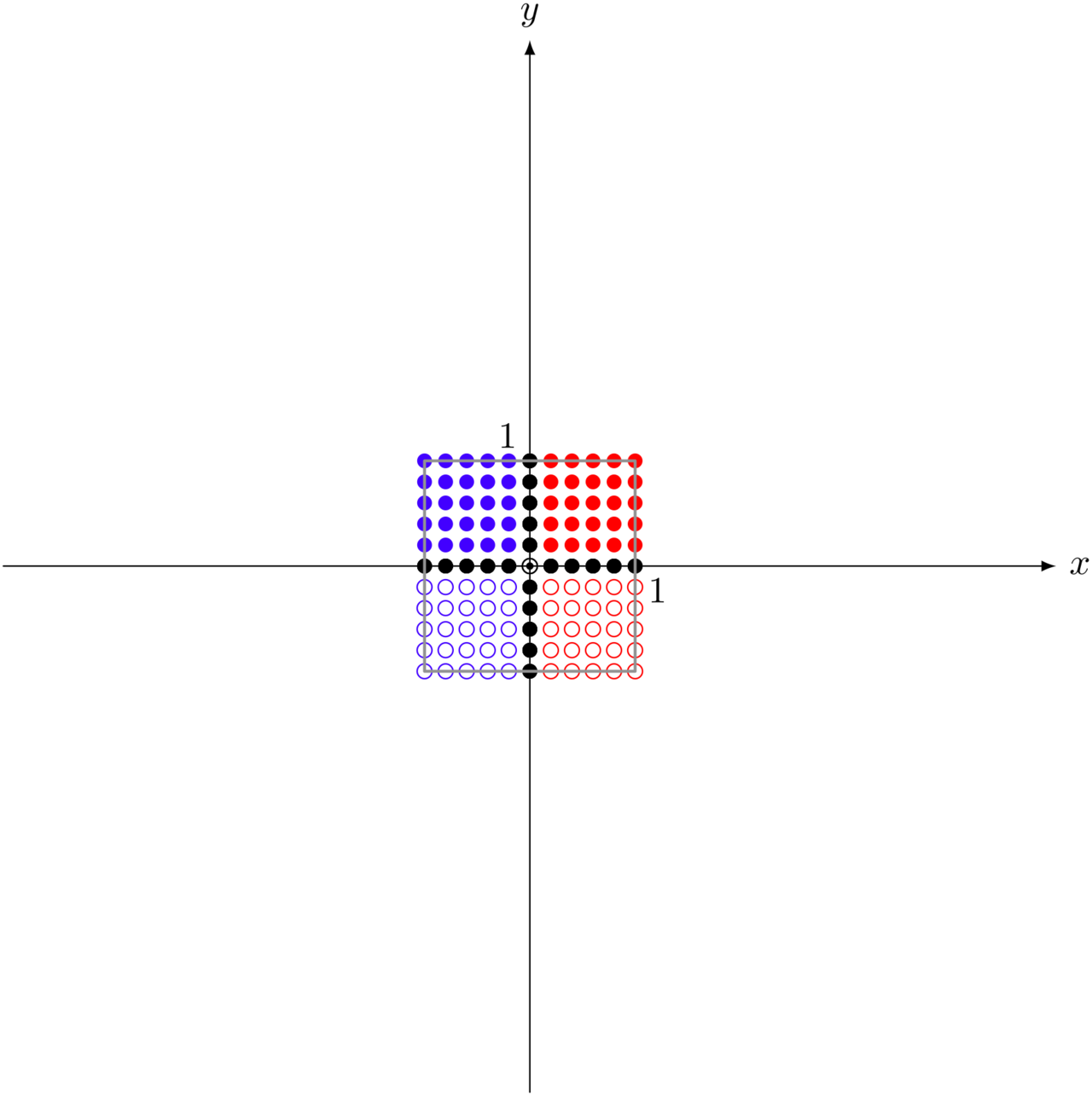
行列 $\left(\begin{array}{cc} 2 & 1 \\ 1 & 3 \end{array} \right)$ による変換
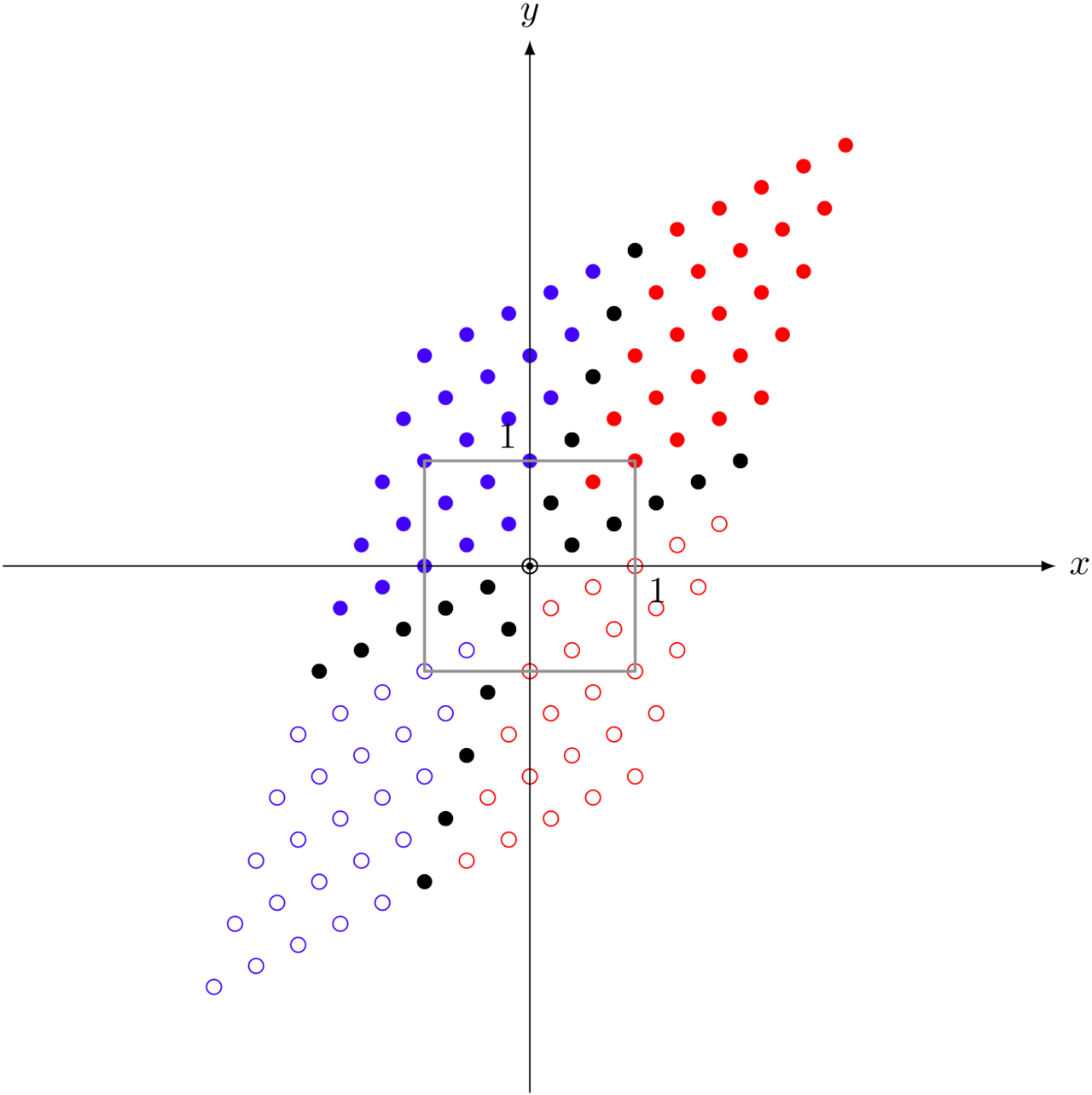
テトラ「行列による《変換の姿》が見えました!」
ミルカ「第121回〜第130回は「やさしい統計」のシーズンだった。 平均、分散、グラフのトリック、それから確率母関数」
僕「連載で入っていた確率母関数は書籍には入ってないね」
ミルカ「その代わりに統計的検定が入ってる」
ユーリ「このシーズンは、やっぱグラフのトリックだにゃあ〜」
僕「こういうのだね(第126回参照)」
αのシェアは何と60パーセント!
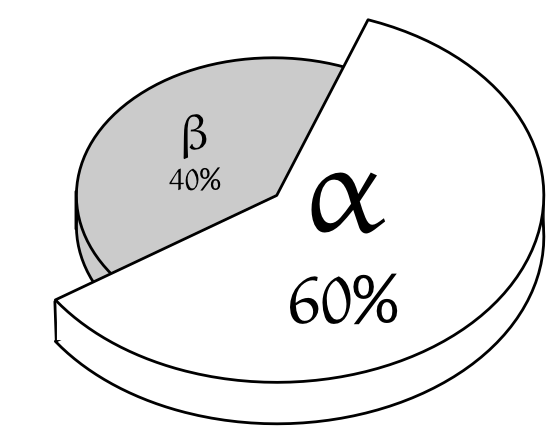
ユーリ「三次元の円グラフ! 商いは、まっとーにやらんとあきまへんで」
ユーリ「第131回〜第140回は「積分を見つめて」のシーズンで、積分を見つめたんだよね」
僕「なんだそりゃ」
テトラ「あたしは……ミルカさんと先輩から《微分積分学の基本定理》を教えていただいたのがやっぱり印象深いです(第135回参照)。 あっ、もちろんそれ以前に定積分のイメージをつかんだことも……」
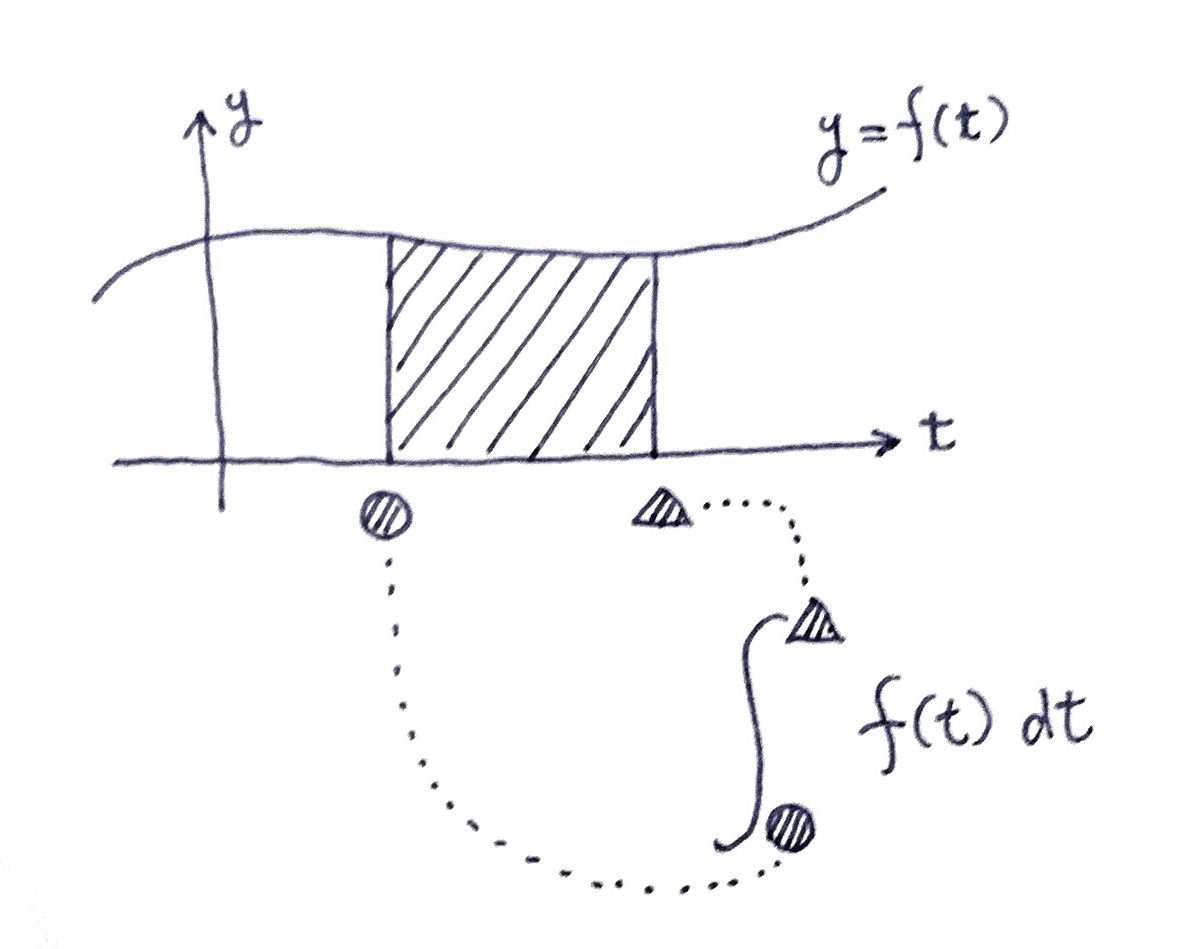
$\heartsuit$ で考える定積分
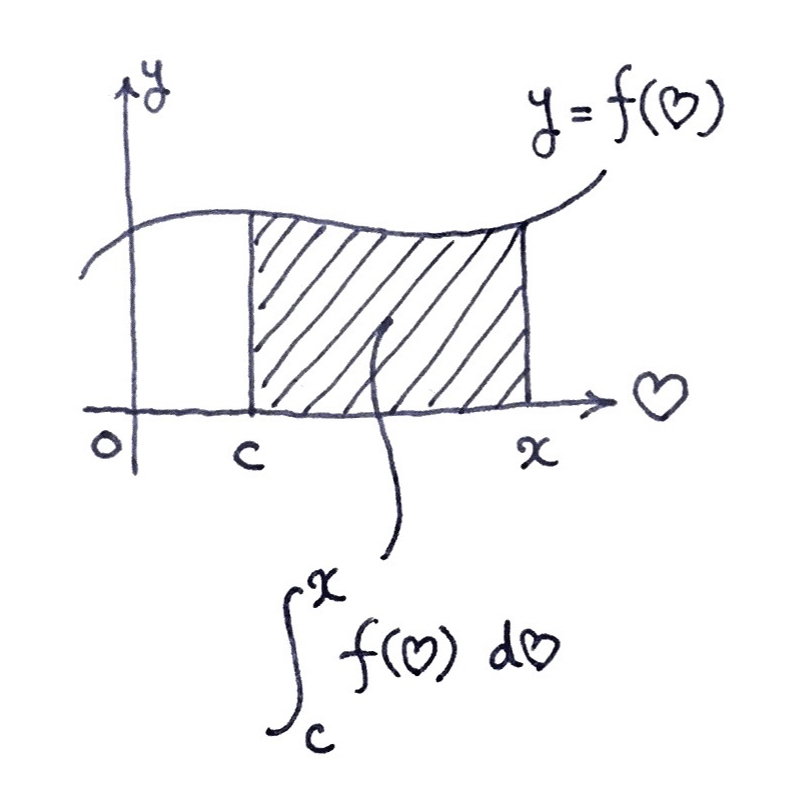
僕「うんうん」
テトラ「この《とろり〜ん》というインテグラルに慣れることができましたっ!」
《とろり〜ん》
ミルカ「第141回〜第150回は「波の広がり」のシーズン。波の基本からフーリエ展開まで」
ユーリ「波の重ね合わせがおもしろかったよ!」
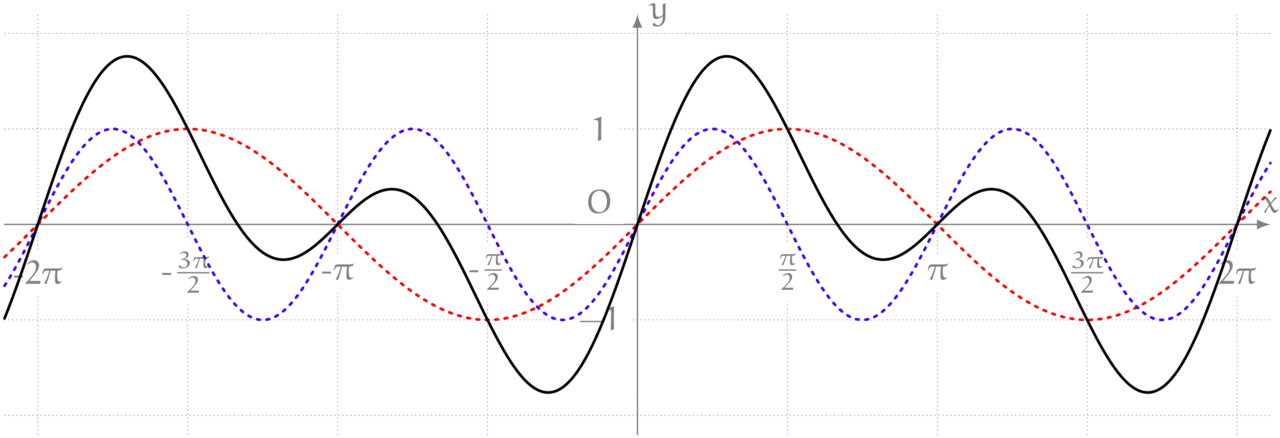
僕「いろんな波を重ねて観察したからね(第145回参照)」
$y = \sin x + \sin 2x$
僕「第151回〜第160回は「数を作る」のシーズン。空集合から始まって、 $p$ 進数の話まで」
ユーリ「《ノイマンの方法》はすごかったにゃあ〜(第151回参照)」
テトラ「空集合から0以上の整数を作っていく方法ですね」
ユーリ「とにかく、カッコがすごいんだよー」
《ノイマンの方法》で構成した3
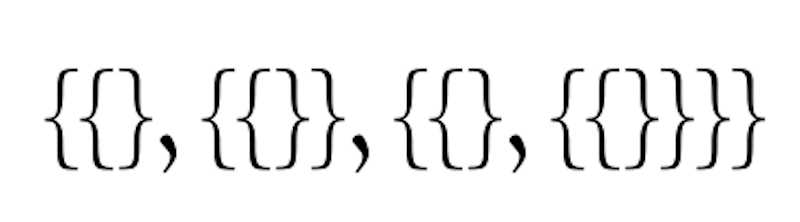
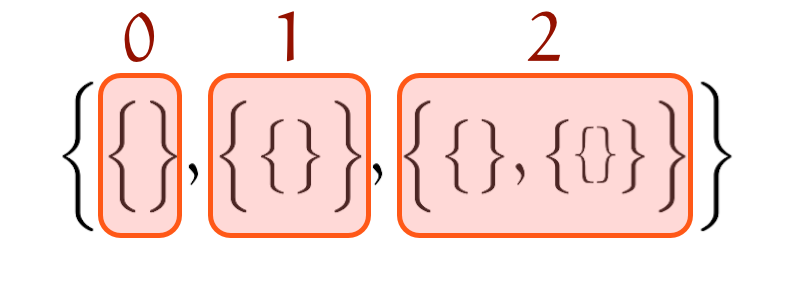
僕「カッコの大きさを微調整すると読みやすくなるね」
《ノイマンの方法》で構成した3
テトラ「第161回〜第170回は「広がる複素数」のシーズンです。 正負の掛け算から始まって、共役複素数、そして行列と四元数までおしゃべりできました」
ミルカ「あれは楽しかった」
僕「テトラちゃんが言ってた《水面に映る星の影》というのも素敵だったよね(第165回参照)」
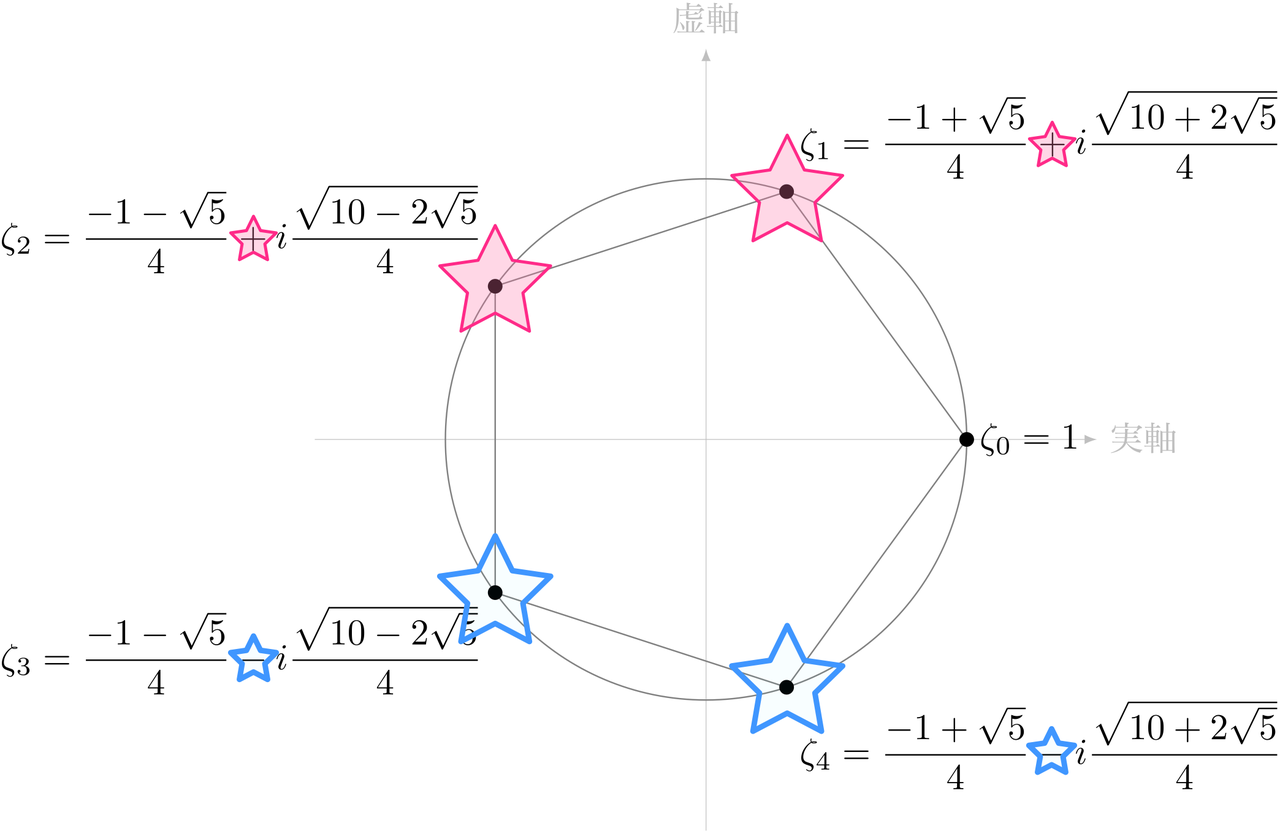
テトラ「き、恐縮です。共役複素数はほんとうにそう感じます。いつも対になって現れますし」
複素平面上、正五角形の頂点に現れる共役複素数
ミルカ「そして、第171回〜第180回は「論理と証明」のシーズン。 カードをめくるクイズから始まって、真理値表とド・モルガンの法則、命題論理と述語論理、背理法と数学的帰納法の話」
僕「ユーリにクイズだしたよね(第171回参照)」
クイズ
片面に整数が書いてあり、
その裏側に動物が書いてあるカードがたくさんある。
その中から取り出した四枚のカードが机の上に並べてある。

[ $13$ ]と[ $40$ ]の裏側には動物が書いてあり、
[猫]と[犬]の裏側には整数が書いてある。
同じ動物や同じ整数が書いてあるかもしれないが、
カードをめくらなければ裏側はわからない。
ここに並べられている四枚のカードが、
以下のルールを満たしていることを確かめるには、
どのカードをめくらなければならないか。
めくらなければならないカードをすべて選べ。
ルール:片面が[猫]ならば、その裏側は奇数である。
(※イラストは「いらすとや」さんから)
ユーリ「あー、やったやった。おもしろかったね」
テトラ「めくらなければならないカードを選ぶ……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第359回終わり)
(2022年5月27日)