![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)
結城浩です。いつも「数学ガール」の応援ありがとうございます。
2022年のcakesサービス終了にともない、 Web連載「数学ガールの秘密ノート」の引っ越しが行われました。 ちょうどよい機会なので、登場人物たちにそれまでの振り返りをしてもらいます。
第359回では「第1回から第180回まで」を振り返り、 第360回では「第181回から第358回まで」を振り返ります。
彼女たちの振り返りを聞いていると、 ずいぶんいろんな話題を話してきたんだなあ……と思います。
それではお楽しみください。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
僕たちは、 思い出深い話題や、印象に残った問題を振り返っている(第359回参照)。
テトラ「第181回〜第190回は「いにしえの数学」のシーズンでした。 双倉図書館でのイベントで、古代エジプト、古代バビロニア、古代ギリシア、そして古代中国の数学についての展示物をまわりました」
ユーリ「パネル展示がたくさんあったんだよね。このクイズがおもしろかった!」
僕「ユーリが即答したクイズだね。これは考えてわかるおもしろい問題だった」
ミルカ「第191回〜第200回は「整数に誘われて」のシーズン。 倍数、約数、最小公倍数、最大公約数、ユークリッドの互除法、素数判定などの話題が出た」
僕「やさしいけれど印象に残った問題はこれだよ。 二人に見つめられた状態でこの問題を考えるのは、正直緊張したなあ」
テトラ「これはリサちゃ……リサが出してくれた問題ですね」
リサ「(頷く)」
僕「問題に対しては正しく答えられたけど、その後の僕の証明……というか説明に《穴》があった。 だから印象に残ってる」
ミルカ「二人に見つめられていたからではなく?」
ユーリ「第201回〜第210回は「関数を手がかりに」のシーズンで、 関数とかー、対応とかー、関数の最大値・最小値とかー……」
僕「地味だけど気に入ってるのはこのクイズかな」
クイズ (第202回参照)
集合 $A$ を $A = \{ 0, 1, 2, 3 \}$ とする。
集合 $N$ を $N = \{ 0, 1, 2, 3, \ldots \}$ とする。
$$ \begin{array}{|c|cccc|} \hline A & 0 & 1 & 2 & 3 \\ \hline N & 123 & 58 & 3028 & 7 \\ \hline \end{array} $$ この表は集合 $A$ から集合 $N$ への関数といえるか。
ユーリ「あーこれね。不安を誘うよねー」
僕「いやいや、関数の《定義にかえれ》で考えればわかるよ」
テトラ「第211回〜第220回は「無限を探そう」のシーズンです。 無限大のお話、無限小数のお話、数学的帰納法のお話、アキレスと亀のお話、極限値のお話など盛りだくさんでした」
ユーリ「ユーリは無限ポテチが食べたかったにゃあ(第211回参照)」

(※イラストは「いらすとや」さんから)
僕「すごい勢いで食べてたからなあ」
テトラ「あたしは、極限値の和の問題が印象深かったです」
問題(極限値の和)(第218回参照)
二つの数列 $\LL p_n \RR$ と $\LL q_n \RR$ は、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & p_n \to 0 \\ n \to \infty & \REMTEXT{で} & q_n \to 0 \\ \end{array} $$ とする。
ここで、数列 $\LL r_n \RR$ の一般項を、 $$ r_n = p_n + q_n $$ で定義する。
このとき、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & r_n \to 0 \end{array} $$ を証明せよ。
ミルカ「なるほど」
ユーリ「$p_n,q_n$ がゼロになるんだから、足してもゼロになるのは当たり前では?」
テトラ「あたしも、最初はユーリちゃんと同じように考えました。 でもそれはとても大ざっぱな考え方でした。当たり前といえば当たり前なんですけど、 『どうして当たり前かをきちんと説明できること』が大事なんです」
ユーリ「できるの?」
テトラ「はい。極限の定義がわかっていると、 『何をいえば証明したことになるか』がわかります。 そこがスタート地点ですね」
僕「第221回〜第230回は「関数を組み立てよう」のシーズン。 微分可能・微分不可能、平均値の定理、ロルの定理、そしてはるばるデデキントの切断、テイラー展開など」
テトラ「あたしは何と言っても、平均値の定理からの壮大な旅が思い出深かったです!」
僕「実数の公理までさかのぼっていった。あれはすごかったなあ」
ミルカ「楽しかった」
ユーリ「どんなのですか、ミルカさま?」
ミルカ「出発点は平均値の定理の証明から」
平均値の定理 (第223回参照)
二つの実数 $a,b$ は、 $a < b$ を満たすとする。
関数 $f(x)$ は、 $a \LEQ x \LEQ b$ で連続とする。
さらに関数 $f(x)$ は、 $a < x < b$ で微分可能とする。
このとき、 $$ \frac{f(b) - f(a)}{b - a} = f'(c) $$ を満たす実数 $c$ が、 $a$ と $b$ のあいだに存在する($a < c < b$)。
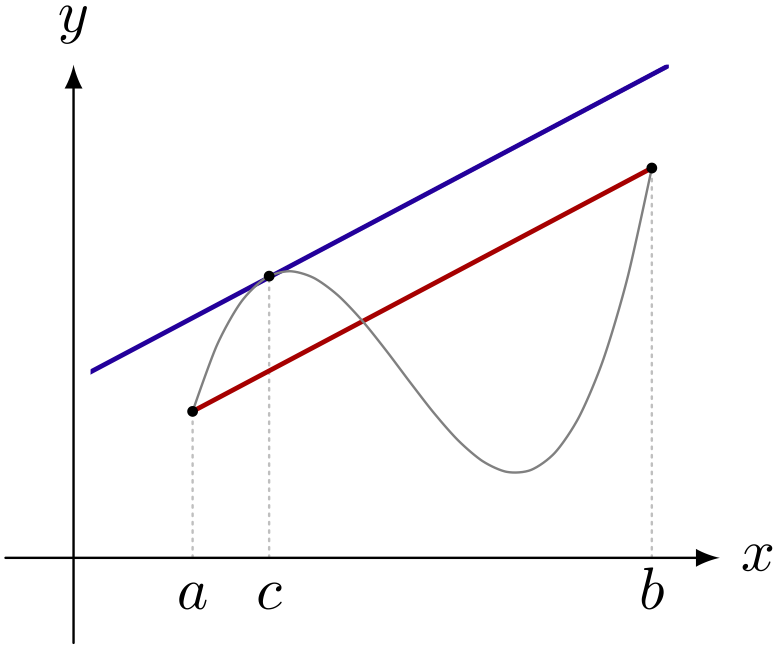
ユーリ「平均値の定理……」
ミルカ「第231回〜第240回は「群とシンメトリー」のシーズン。 サイコロの置き方を皮切りに正六面体群を詳しく調べていく。そのほかに巡回群、剰余群、部分群とラグランジュの定理、そして群の作用まで」
ユーリ「24通りのサイコロの置き方を、いろいろ考えたよ!」
テトラ「サイコロの置き方が《群》につながっていくのは驚きでした」
ミルカ「対称性があるところに《群》は顔を出す」
僕「第241回〜第250回は、いよいよ「学ぶための対話」のシーズンだね」
ユーリ「ノナ! ノナ! 出番だよー!」
ノナ「え、あ……こんにちは $\NONA$」
登場人物紹介(追加)
ノナ:ユーリの同級生。 ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。 数学は苦手だけど、興味を持ってる中学生。
僕「こんにちは。お久しぶり。ノナちゃんの、思い出深い話題があったら紹介してくれる?」
ノナ「話題って……どんな話題ですか $\NONAQ$」
ユーリ「何でもいーんだよん。問題でも、クイズでも。ほれほれ、あるじゃん。アレとかコレとか」
ノナ「mgn $\NONAQ$」
僕「はい?」
ノナ「無限……《無限のキャンバス》$\NONA$」
僕「ああ、座標平面が《無限のキャンバス》になっているという話だね(第241回参照)。どれほど遠いところにも点を描くことができる」
ノナ「どんな紙よりも広くて……どこまでもどこまでも広がってます $\NONA$」
テトラ「座標平面に描かれる直線と式の関係や、一次方程式の話や、 そして何より《理解する》ということについて。 ノナちゃんと、先輩と、ユーリちゃんの《学ぶための対話》ですね!」
テトラ「第251回〜第260回は「確率の冒険」のシーズンでした。 確率の基本から、条件付き確率、そして歴史的なメレの問題までが話題になりました。 あ、あたしは何と言っても偽陽性・偽陰性の問題が印象深かったですね……」
ユーリ「ユーリは、相対度数と確率かにゃあ……」
テトラ「と言うのは?」
ユーリ「コインを $M$ 回投げて表が $m$ 回出たときの $m/M$ だけど、 これは確率じゃなくて、相対度数だって話(第252回参照)。 お兄ちゃんから言われてほほー……ってなった」
僕「相対度数と確率は式は似ているけど、意味はまったく違うからね」
ミルカ「第261回〜第270回は「分数を極める」のシーズンだ。 フィボナッチ数列、黄金比、連分数、表記と値、表現と意味……といったところか」
テトラ「黄金比を求めるための二次方程式が、連分数の形にぴったり当てはまるというのは感動しました」
僕「黄金比はフィボナッチ数列とも関連していたね(第261回参照)」
ミルカ「どこにも出てくるフィボナッチ」
リサ「好き」
テトラ「第271回〜第280回は「放物線をつかまえて」のシーズンです」
僕「これはいろいろ楽しかったなあ」
ユーリ「モンキーハンティング、すごかった。ユーリ、一発で当てたよね!」
問題 (第279回参照)
原点から水平方向に $X$ だけ離れたところに木がある。
高さ $Y$ のところにリンゴがなっている。
リンゴの《質量》を $m$ とする。
原点から、木のほうに向かってボールを投げる。
ボールを投げた瞬間の《速度》の大きさを $V$ とする。
ボールを投げる向きは、角度を $\theta$ とする。
ボールを投げる瞬間の《時刻》を $t = 0$ とする。
ボールの《質量》を $M$ とする。
ボールを投げた瞬間に、リンゴが木から落ちるとする。
落ちていくリンゴにボールを当てるためには、 $V$ と $\theta$ をどうしたらいいか。
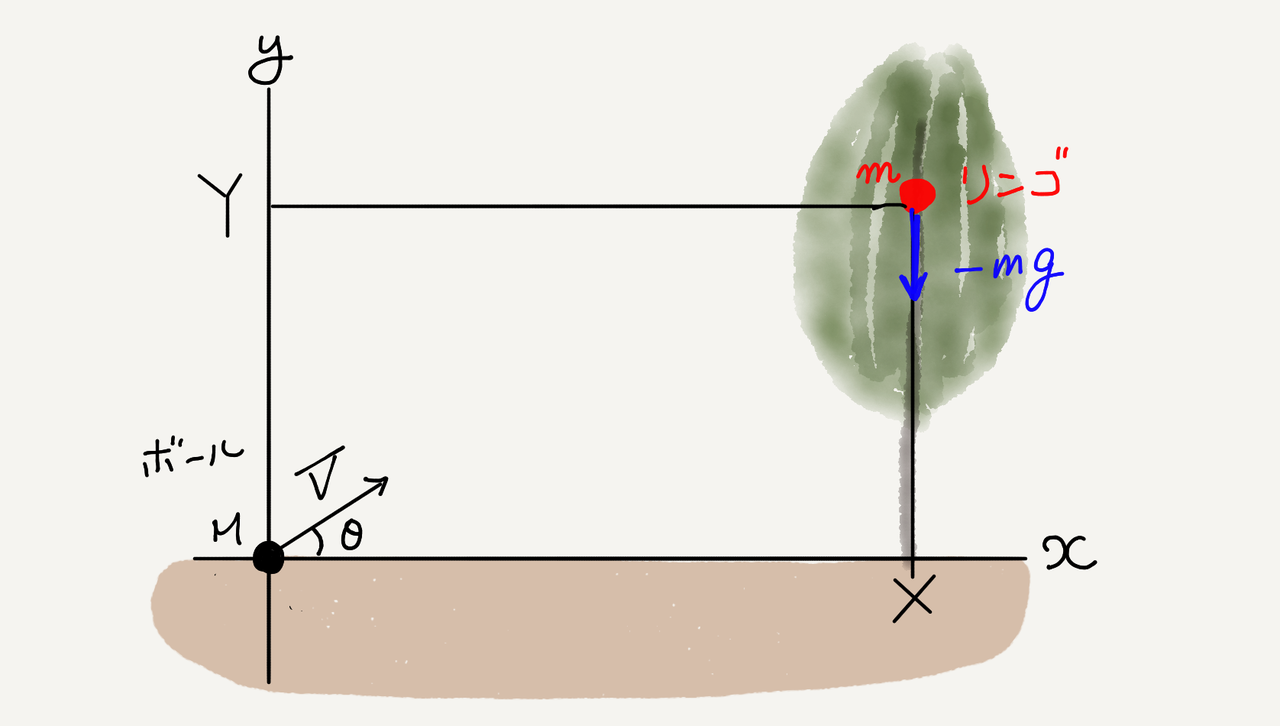
重力加速度は $-g$ とする。
僕「《選ばれしもの》なるユーリの慧眼がすべてを見抜いたんだな」
ユーリ「何そのファンタジー」
テトラ「このシーズンは初の物理ノートとなりました! 等速度運動、等加速度運動、ニュートンの運動方程式、万有引力の法則、運動エネルギーと位置エネルギー、力学的エネルギー保存則、そしてケプラーの法則まで!」
ミルカ「第281回〜第290回は「音楽と数学」のシーズン。 音が波であること、ピタゴラス音階、平均律、ピタゴラスコンマ、純正律、そしてオイラー格子の登場となる」
ユーリ「音階の話や、対数の話もおもしろかったけど、いっちばんカッコよかったのはファレイ数列かにゃあ」
僕「第291回〜第300回は「グラフ理論」のシーズンで、 たくさんのゲームやパズルを解いたね。 連結ゲーム、未来都市通信網パズル、施設の機材管理パズル、あとは……」
ミルカ「五色問題」
テトラ「《直線国境諸国巡遊偶数回横断問題》もありましたよっ!」
僕「あったね……」
ユーリ「《連結ゲーム》では、例によって、お兄ちゃんがリフジンなルールで、いたいけなユーリを、いじめたんだよにゃあ! テトラさん、言ってやって言ってやって!」
テトラ「どんなルールなんですか?」
僕「《連結ゲーム》はこんなルール。そしてユーリは必勝法に気づいたんだよ」
《連結ゲーム》のルール (第291回参照)
プレイヤーは二人。 紙に $1$ 個以上の頂点を描き、交互に二頂点を結ぶ辺を描く。 先に描けなくなったプレイヤーが負けである。
辺を描くときのルールが三つある。
ルール1:辺は多重にしない
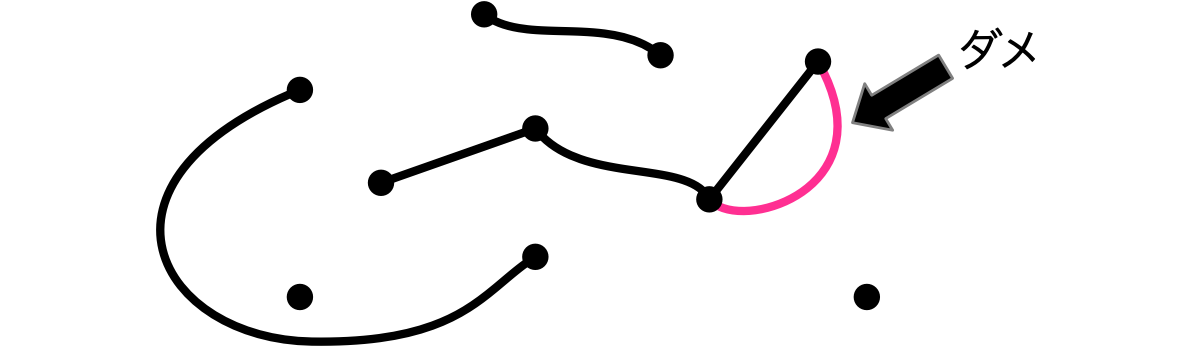
ルール2:ループを作らない
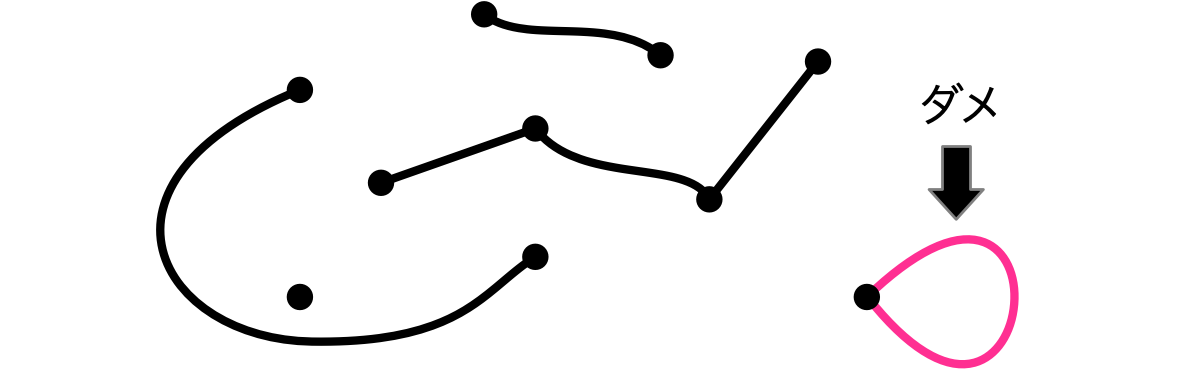
ルール3:サイクルを作らない
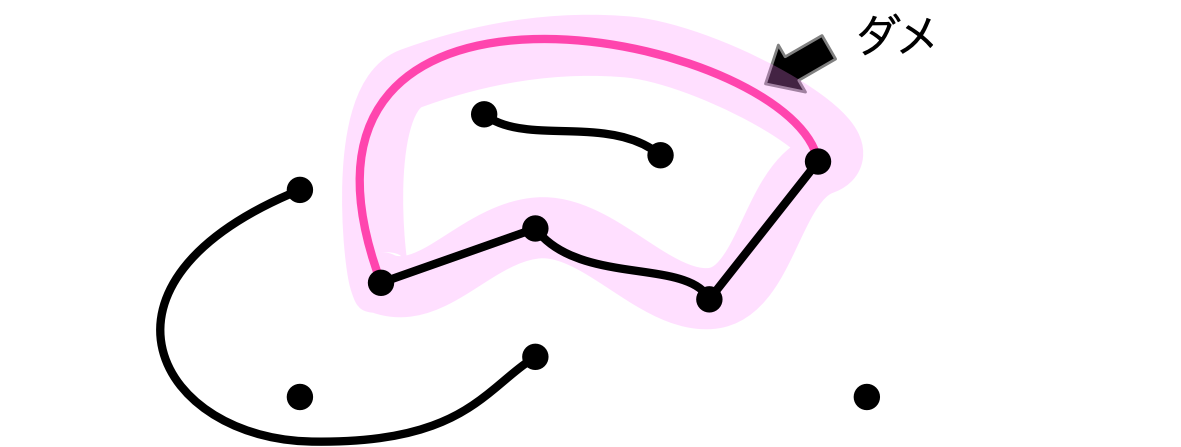
テトラ「必勝法……?」
ユーリ「あのね、点の個数でね……」
ノナ「あの……第301回から第310回まではノナが出ました $\NONA$」
ユーリ「読むための対話シーズン……ってサブタイトルだったんだ」
僕「本では『図形の証明』になっていたね。三角形の合同を中心に、証明というものについておしゃべりしたけど、ノナちゃんはどうだった?」
ノナ「理由……理由が大事です $\NONA$」
ユーリ「証明は、理由が伝わるように書くってことっしょ?」
ノナ「あいまいはだめ……あいまいになってはだめです $\NONA$」
僕「そうそう。合同条件でも出てきたね。 二つの三角形があって、 『二組の辺の長さがそれぞれ等しくて、その辺ではさまれている一組の角の大きさが等しい』という合同条件。 《二つの辺》と《一つの角》とだけ言ってしまうと、その角がどこの角かわからなくなってしまう」
二辺夾角相等ならば合同
二組の辺の長さがそれぞれ等しくて、その辺ではさまれている一組の角の大きさが等しいならば、 その二つの三角形は合同である。
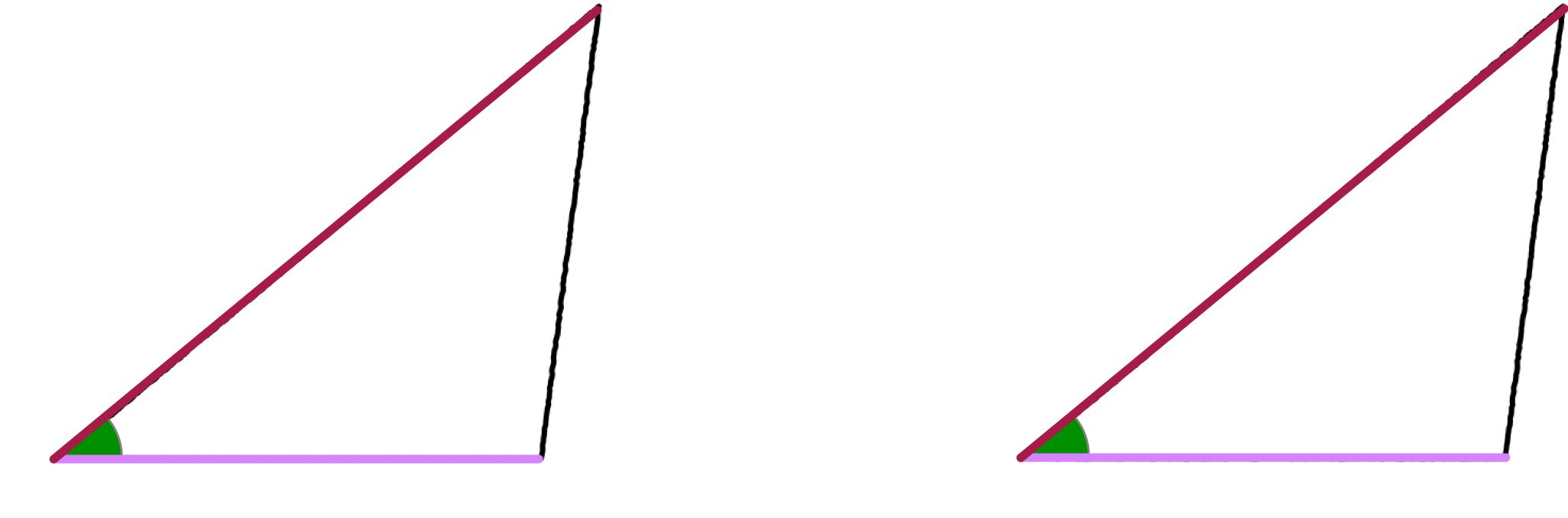
ただの《角》といってしまうと、どこの角のことかはっきり決まらない
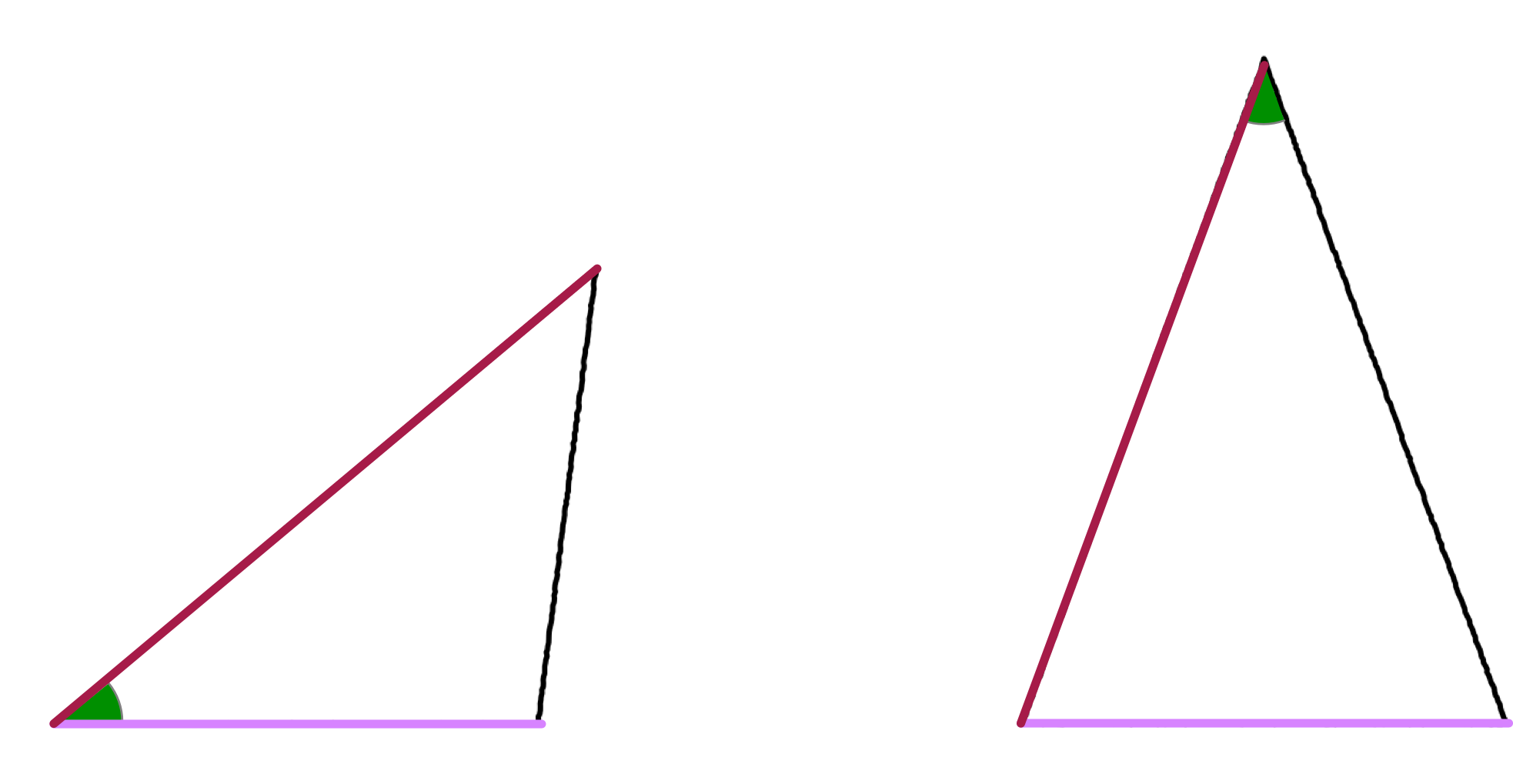
ノナ「あいまいです $\NONA$」
僕「そう、そうなんだ。証明は、あいまいにならないように、はっきりと伝わるように書く」
テトラ「三角形の合同条件、三角形の分類、平行線の錯角と同位角などの話題で、 定義がとても大切な理由、 証明をする目的、 証明はどんなふうに書くのか、 そして未知の問題に出会ったときにどのように考えていくのか。 ノナちゃんが中心になった数学対話です!」
ユーリ「第311回〜第320回は「ふれあう三角関数」のシーズンだったけど、 どこが《ふれあう》なんだろ」
ミルカ「タンジェント $\tan$ がテーマだからだろうな」
ユーリ「タンジェント……?」
テトラ「tangentはもともと《接している》や《接触している》という意味ですね」
ユーリ「それで《ふれあう》なんだー」
テトラ「ユーリちゃんは $\tan$ もこなしちゃうんですね。すごいです」
ユーリ「へへー……でも簡単だったよ。円を描けばすぐにわかるもん! これが $\tan$ の定義でしょ?(第311回参照)」
$$ \tan\theta = \frac{\sin\theta}{\cos\theta} $$
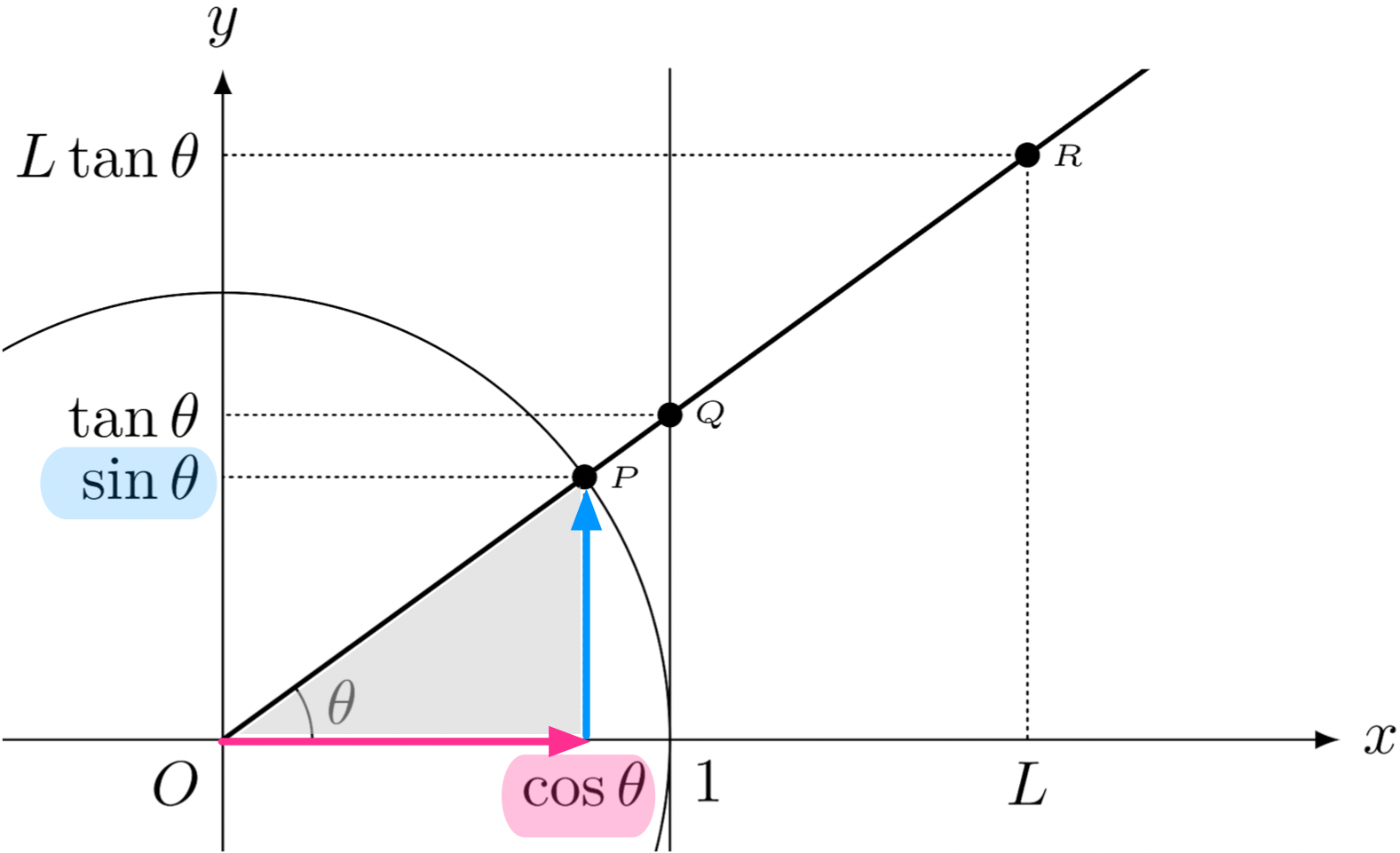
テトラ「はい、そうですね」
ユーリ「そしたら、この点Qの $y$ 座標が $\tan\theta$ になるよね。分母が1だから」
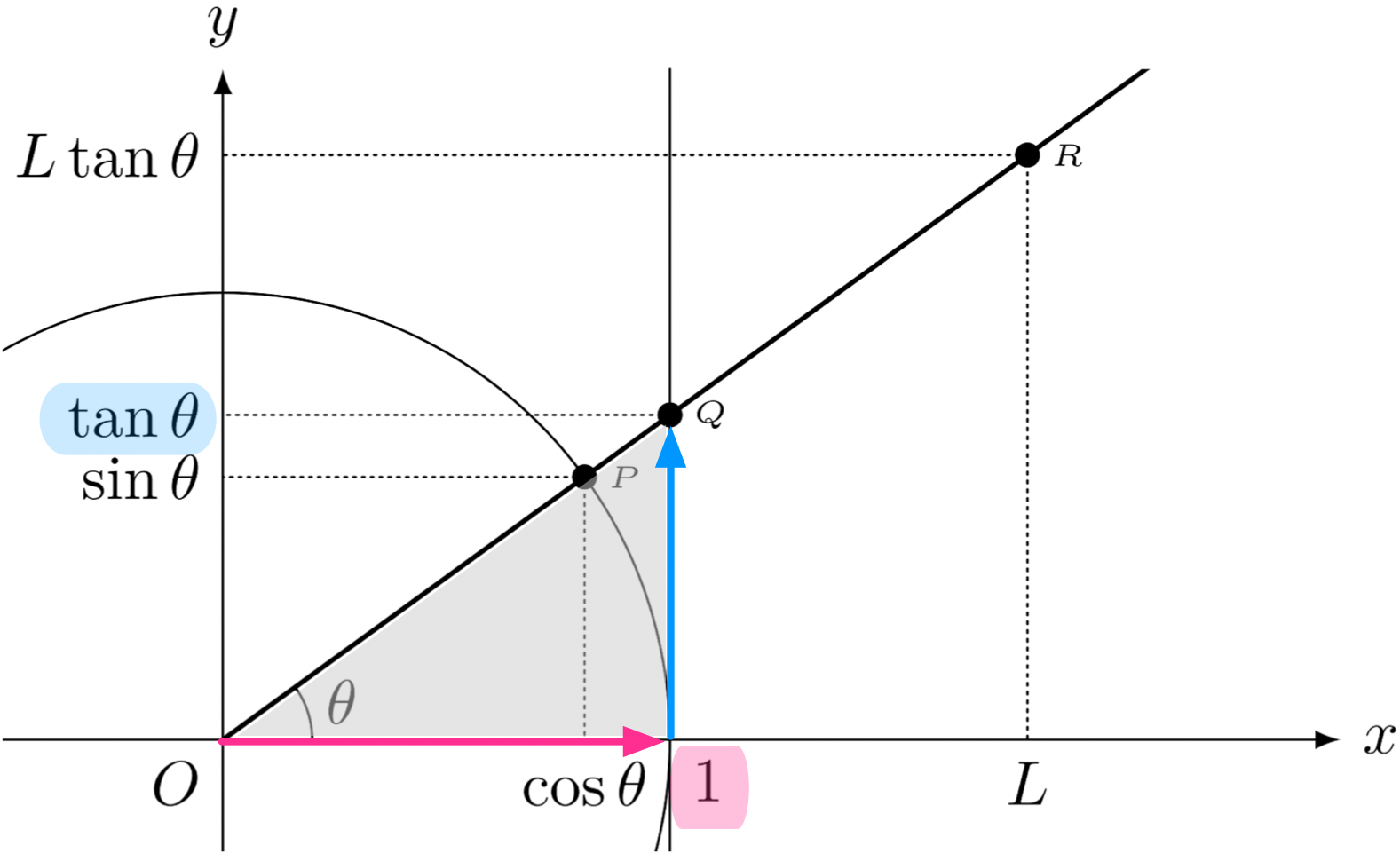
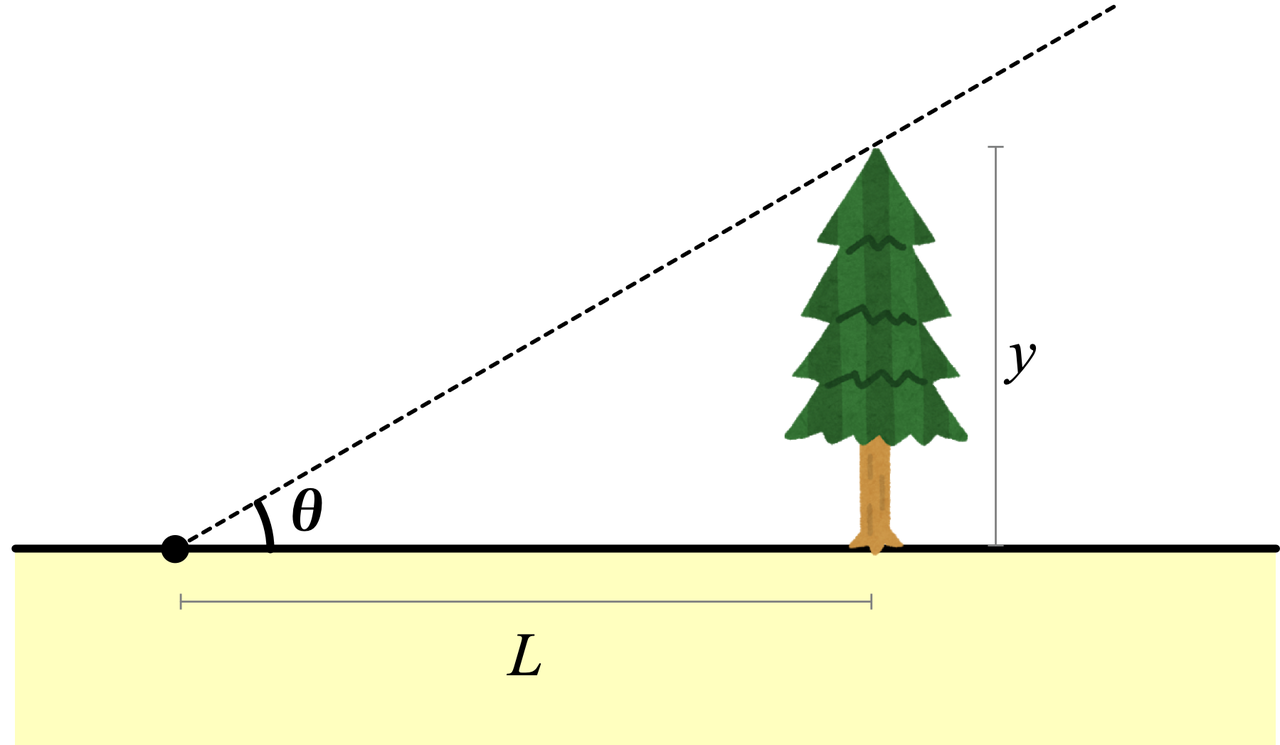
僕「相似だからね。それで、木の高さは $y = L\tan\theta$ で求められる」
テトラ「あとは $\tan$ の加法定理を求めたり、それから複素数の楽しい計算も出てきましたね……」
僕「第321回〜第330回は「楽しいアルゴリズム」のシーズンで、テトラ先生の講義だったね。僕がたくさん教わったんだ」
リサ「リンクとストラクチャ?」
テトラ「そうです、そうです。双倉図書館であたしが学んだことを、 僭越ながら先輩にお伝えしたのでした」
僕「盛りだくさんだったよ。リストを作ったり、最大値を求めたり、スタックやキューなどのデータ構造を学んだり、二分探索木に、それから……」
リサ「トリープ」
テトラ「印象に残ったこと、何かありますでしょうか」
僕「しょっぱなから、大きな誤りを見逃したことかなあ。MAX-VALUEを求めるアルゴリズム」
テトラ「あたしもまちがえたものですね」
僕「うーん……それから、テトラちゃんに教えてもらいながら、僕は馬鹿だなあと思うことはよくあったよ」
テトラ「えっ?」
僕「テトラちゃんがさんざん《図を描いて考えて》といってるのに、 リンクを付け替えるプログラムを考えるときにも図を描かなかったからね……たとえばテトラちゃんは、こういう図をちゃんと描いているのに(第323回参照)」
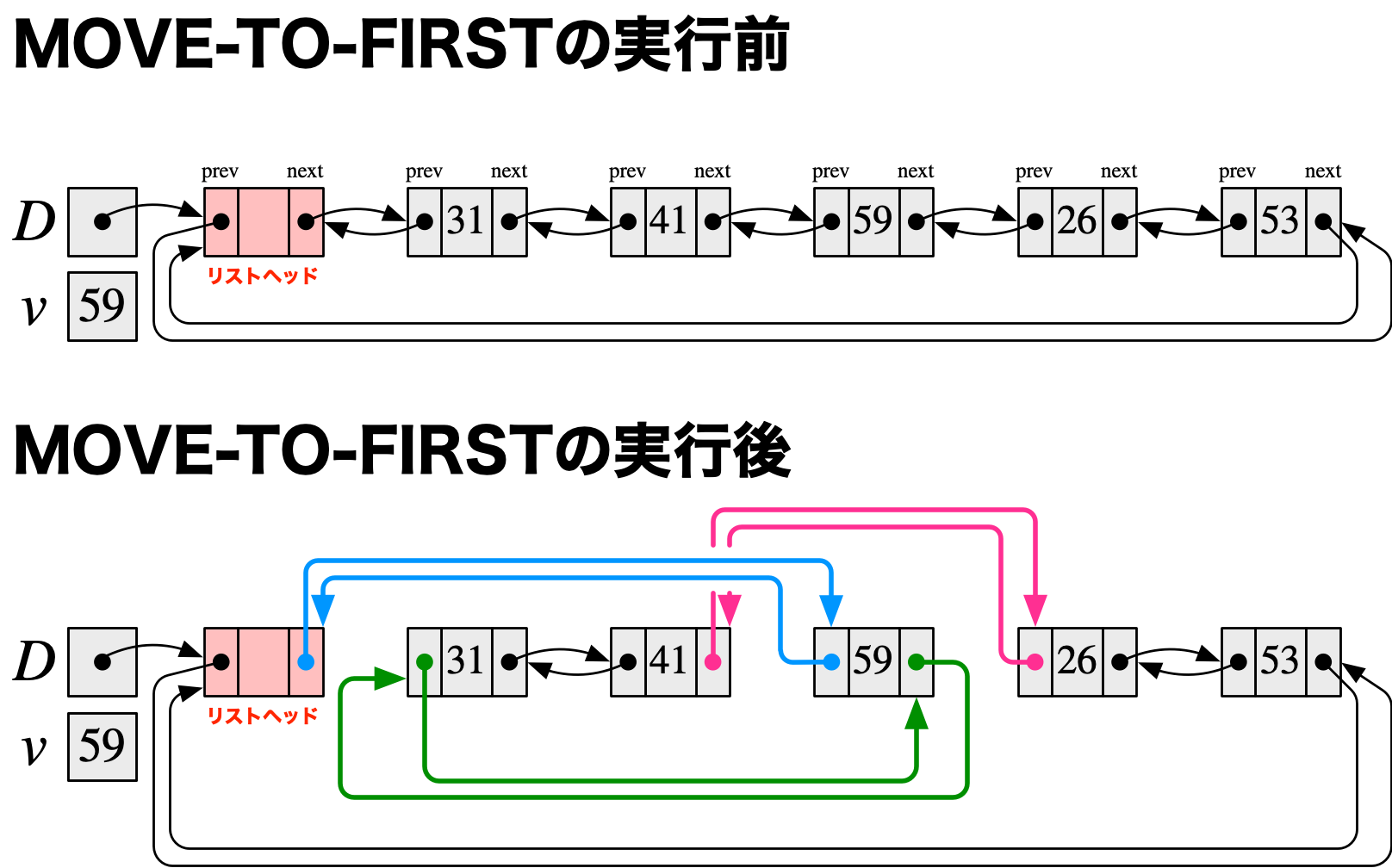
テトラ「……」
僕「僕は、手を動かさずに頭の中だけで考えようとする大馬鹿者だなあって」
テトラ「そ、そんなことおっしゃらないでくださいっ!」
ユーリ「(お兄ちゃんの自虐モード、めずらしー……)」
ミルカ「(そうでもない)」
ミルカ「第331回〜第340回は「電気」のシーズン。 電池の直列つなぎに並列つなぎ、オームの法則、電流、電圧、クーロンの法則、電気力線、キルヒホッフの法則、電場と位置エネルギー」
ユーリ「印象に残った話、ユーリが言ってもいい?」
テトラ「もちろん、どうぞ」
ユーリ「あのね。100億個のビーチボールの話!(第332回参照)」
テトラ「100億個のビーチボール……?」
僕「豆電球を点灯させる回路で流れている自由電子の個数の話をしていたんだ」
ユーリ「そーそー!」
テトラ「100億個もあるんですか!」
ユーリ「テトラさん、ちがうの。100億個×100億個」
テトラ「えっ?」
僕「10の20乗くらいのオーダーじゃないかなって、ユーリに話したんだよ。 10の20乗ってわかりにくいから、地球をこんなふうにビーチボールみたいなものだと考える」

テトラ「はい」
僕「世界にいる100億人全員がビーチボールみたいな大きさの地球を抱えているとする」
ユーリ「じゃじゃーん! 100億個のビーチボール!」

僕「100億個のビーチボールの上には、100億人の《小さな人》が住んでいると考えると……《小さな人》の数はぜんぶで100億×100億になる。 それで $10^{20}$ のオーダーになるという話」
テトラ「すごいですね……!」
ミルカ「第341回〜第350回は「熱力学」のシーズン。 アルキメデスの原理、アボガドロの法則、ボイルの法則、シャルルの法則、理想気体の状態方程式、 熱力学の第一法則と第二法則、ケルビンの原理、カルノーサイクル」
テトラ「あたしの最大衝撃は熱でした!」
僕「そうなんだ」
テトラ「ボイル=シャルルの法則や気体分子運動論などでたくさんの物理量が出てきました。 速度・運動量・力積・運動エネルギー・圧力・体積・物質量・温度……でも、 肝心かなめの《熱》が出てきてないことに気づいていませんでした。 あれはショックでした」
僕「熱はわかっているつもりになっちゃうから、かえって難しいよね」
ユーリ「ユーリはねー、浮力の話がびっくりだった。《軽い木の人形》と《重い鉄の人形》で浮力が同じ!」
テトラ「確かにそうですね。アルキメデスの原理です」
僕「そして、第351回〜第360回は「不可能問題への挑戦」のシーズンだったね。 多角形と面積が等しい正方形を作ること、円積問題、立方体倍積問題……最後の第359回と第360回は《みんなで振り返る会》になった」
ユーリ「うんうん」
僕「立方体倍積問題は解けないことがわかってるけれど、 《定規とコンパスを有限回使う》という条件を外すとおもしろい世界が広がってた」
ユーリ「やっぱり、なんつってもアルキュタスの解法がサイコー!」
僕「立体の交点だね」
アルキュタスの解法 (第358回参照)
二つの比例中項を求めるアルキュタスの作図は、三次元的に行われる。
三つの立体面の交点として求める点を作図するからである。
三つの立体面とは、
である。
ユーリ「先を読まない《予言者読み》と、一歩一歩読んでく《探険者読み》が楽しかった!」
瑞谷先生「下校時間です」
登場人物紹介(追加)
瑞谷先生:司書の先生。定時になると下校時間を宣言する。
ノナ「あ $\NONA$」
ユーリ「わーん! 終わっちゃったよー!」
テトラ「そうですね……」
僕「でも、僕たちの《数学トーク》が終わったわけじゃないよ」
ミルカ「そうだ。これからも、ずっと続く」
リサ「コンティニュー」
母「はい、お疲れさま。じゃ、みんなでお茶にしましょう!」
登場人物紹介(追加)
母:「僕」の母。
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第360回終わり)
(2022年6月3日)