![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ねー、お兄ちゃん!」
僕「『なんか、おもしろい話、ないのー?』」
ユーリ「あっ、何それ。人のセリフ取るなよー!」
僕「さっきからユーリがたいくつそうな顔してるから、そろそろそんなセリフが出てくるかなあって思ったんだよ」
ユーリ「そーゆー、人の行動を見透かすよーなのは嫌われるんだぞ」
僕「はいはい」
ユーリ「なんか、おもしろい話、ないのー?」
僕「結局、言うんかい」
ここは僕の部屋。
いつものようにユーリが遊びに来ている。
ユーリ「それで? お兄ちゃん、ユーリは退屈していますよ?」
僕「リュックを背負って迷子になってる小学生みたいなセリフだな」
ユーリ「ちょっと何言ってるかわかんない」
僕「そうだなあ……じゃあ、こんな問題はどうだろう」
問題1
与えられた三角形に等しい面積を持つ正方形を作図する方法を考えよ。
ユーリ「来た来た。ちゃーんと出てくるんだから……でも、これはカンタン過ぎ!」
僕「おっと、そんなに簡単か?」
ユーリ「こんなふうに線を引いて、切り取って移動すればいーでしょ?」
ユーリの解答1(?)
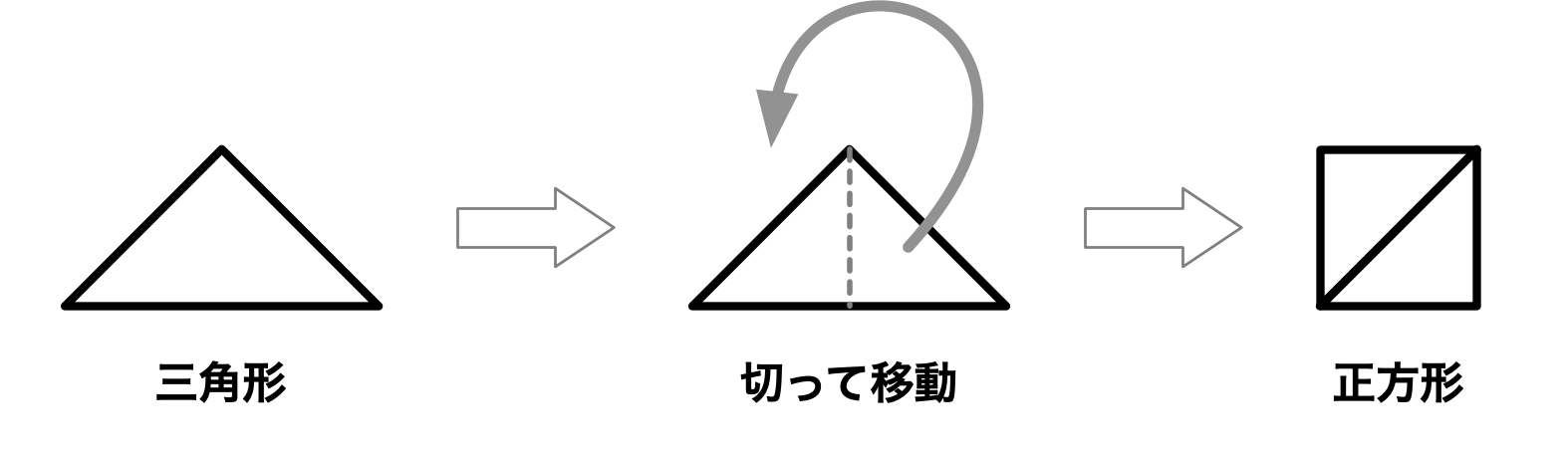
僕「え?」
ユーリ「だって、切り取って移動しただけだから、面積は等しくなるじゃん?」
僕「いやいや、確かに面積は等しいけど、 いまユーリが変形したのは直角二等辺三角形だよね。 一つの角が直角になっていて、しかも二つの辺の長さが等しい三角形。 そういう特殊な三角形の場合は、いまの方法でもいいよ」
ユーリ「あ……」
僕「そりゃもちろんそうなんだけど、 この問題1が求めているのはそれだけじゃない。 直角二等辺三角形に限らず、 どんな三角形が与えられても それと等しい面積を持つ正方形を作図してほしいということなんだから。 三角形といってもいろいろある」
ユーリ「あーそだね。ちょっと勘違いしただけじゃん。 でも、直角二等辺三角形も三角形だし、この方法はまちがいじゃないよね」
僕「そうだね。直角二等辺三角形の場合にはこれで等しい面積の正方形ができる。 じゃあ、続けて考えてみてよ」
ユーリ「へーい」
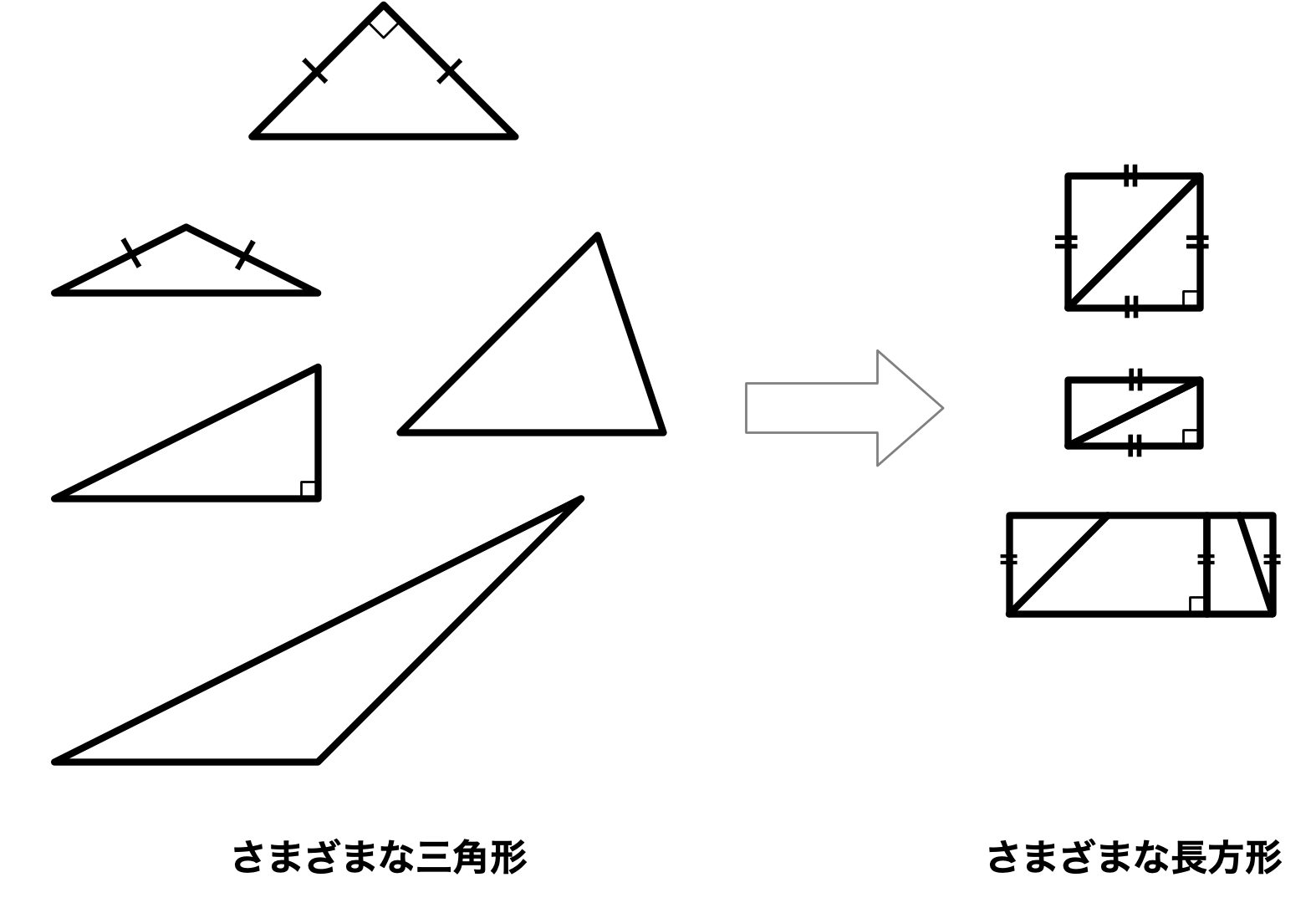
そしてユーリは深い思考モードに入っていった。 思考モードというよりも、試行モードだな。 机に用意してあるA4のコピー用紙を使って、いろんな図を描き始めた。
さまざまな三角形を、正方形に変形しようとしているようだ。

僕「……」
ユーリ「うー……」
僕「苦悩するユーリ」
ユーリ「茶化すなよー」
僕「ごめんごめん」
ユーリ「あのね、聞いて聞いて!」
僕「はいはい」
ユーリ「すごく惜しーところまで来たんだよ。長方形まではいくんだけどにゃあ!」
僕「どう考えたか、教えてよ」
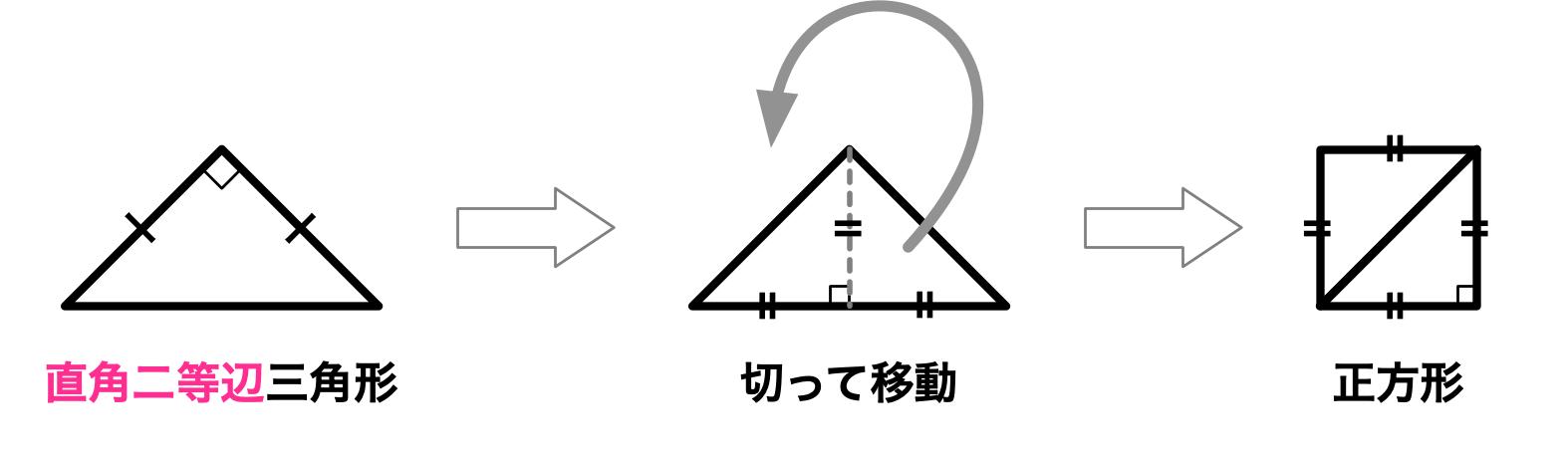
ユーリ「直角二等辺三角形じゃなくて、ただの二等辺三角形のときを考えたの。 縦に切って片方を移動する。そーすると、正方形じゃないけれど、長方形になる」
二等辺三角形を正方形にしたいけど、とりあえず長方形にする
僕「うん。 《縦と横が等しい》という条件は付かなかったわけだね。 縦と横が等しい長方形になってくれれば正方形なんだけど」
ユーリ「そゆこと、そゆこと。で、長方形を正方形に直すのはあとで考えることにして、 他の三角形も試してみよーと思った」
僕「とてもよくわかる。ユーリ、すごいなあ!」
ユーリ「え、そんなにすごい? まだできてないよ」
僕「そうじゃなくて、自分の考える道のりをぜんぶ説明できるところがすごい!」
ユーリ「へへー。もっとホメて」
僕「このくらいで」
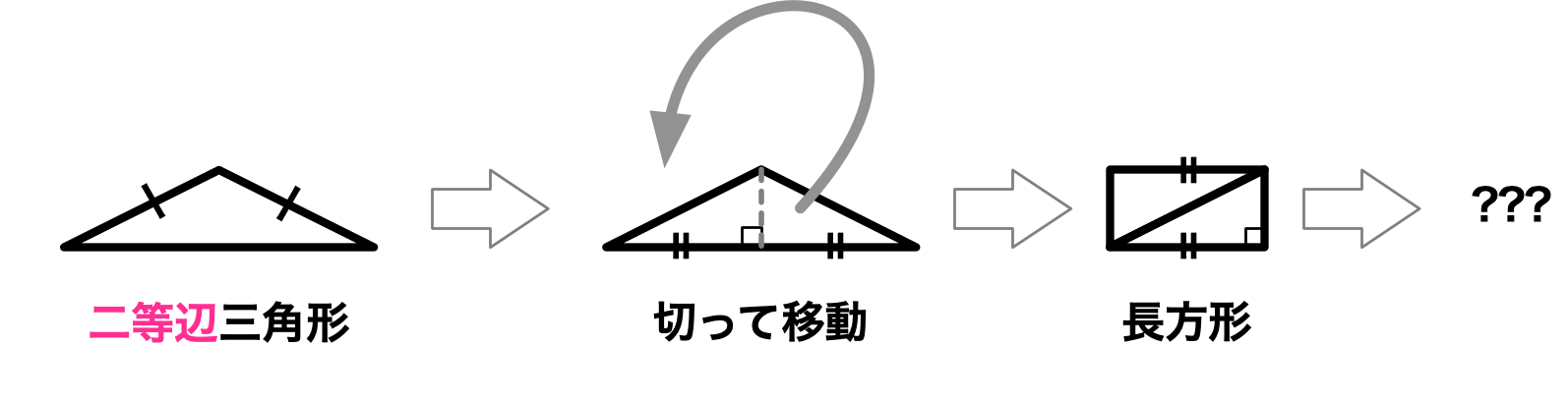
ユーリ「ちぇっ。……でね、次は二等辺じゃない直角三角形を試したよ。 今度はね、別の切り方をしたの」
直角三角形を正方形にしたいけど、とりあえず長方形にする
僕「横に切ったんだ」
ユーリ「うん。もうね、正方形にするのはあとでまとめて考えることにしたから、 長方形にするのをめざしたんだよ」
僕「うんうん」
ユーリ「でね、あとは直角三角形でもないし、二等辺三角形でもない三角形でしょ?」
僕「そうだね。いよいよ一般の三角形だ」
ユーリ「それはね、聞いてよ聞いてよ」
僕「さっきからずっと聞いてるじゃないか」
ユーリ「縦に切ると二つの直角三角形ができるから、それを両方とも長方形にしちゃえばいい!」
一般の三角形を正方形にしたいけど、とりあえず長方形にする
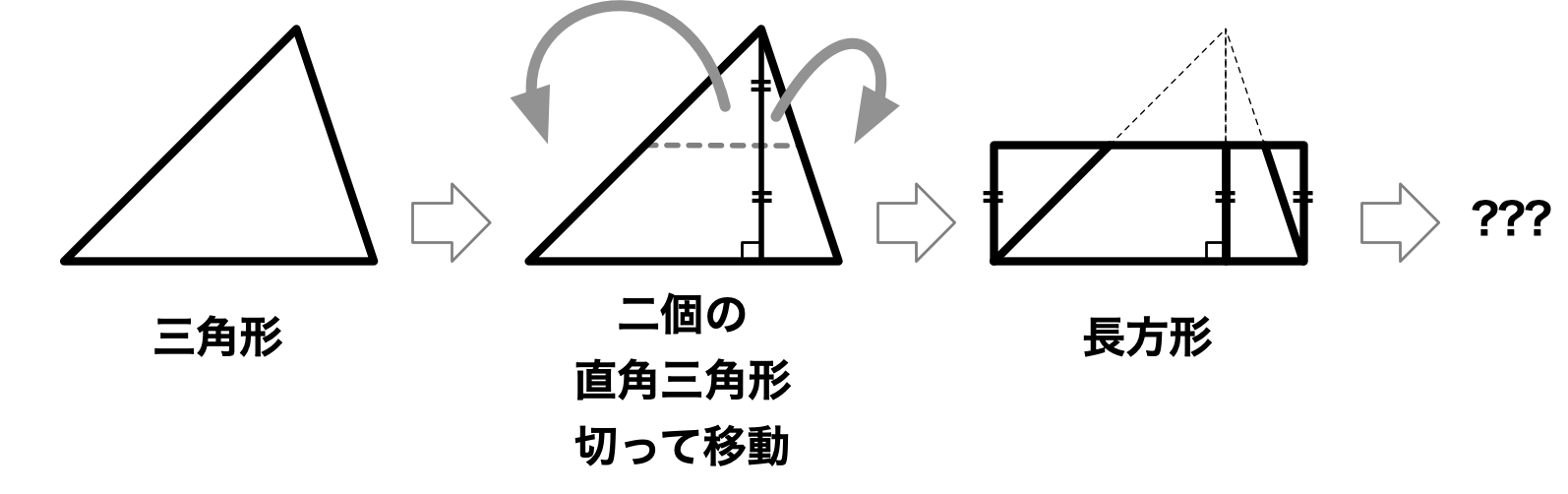
僕「いいね! 僕はこんなふうにいったん平行四辺形にしてから考えたよ」
三角形を平行四辺形にしてから長方形にする
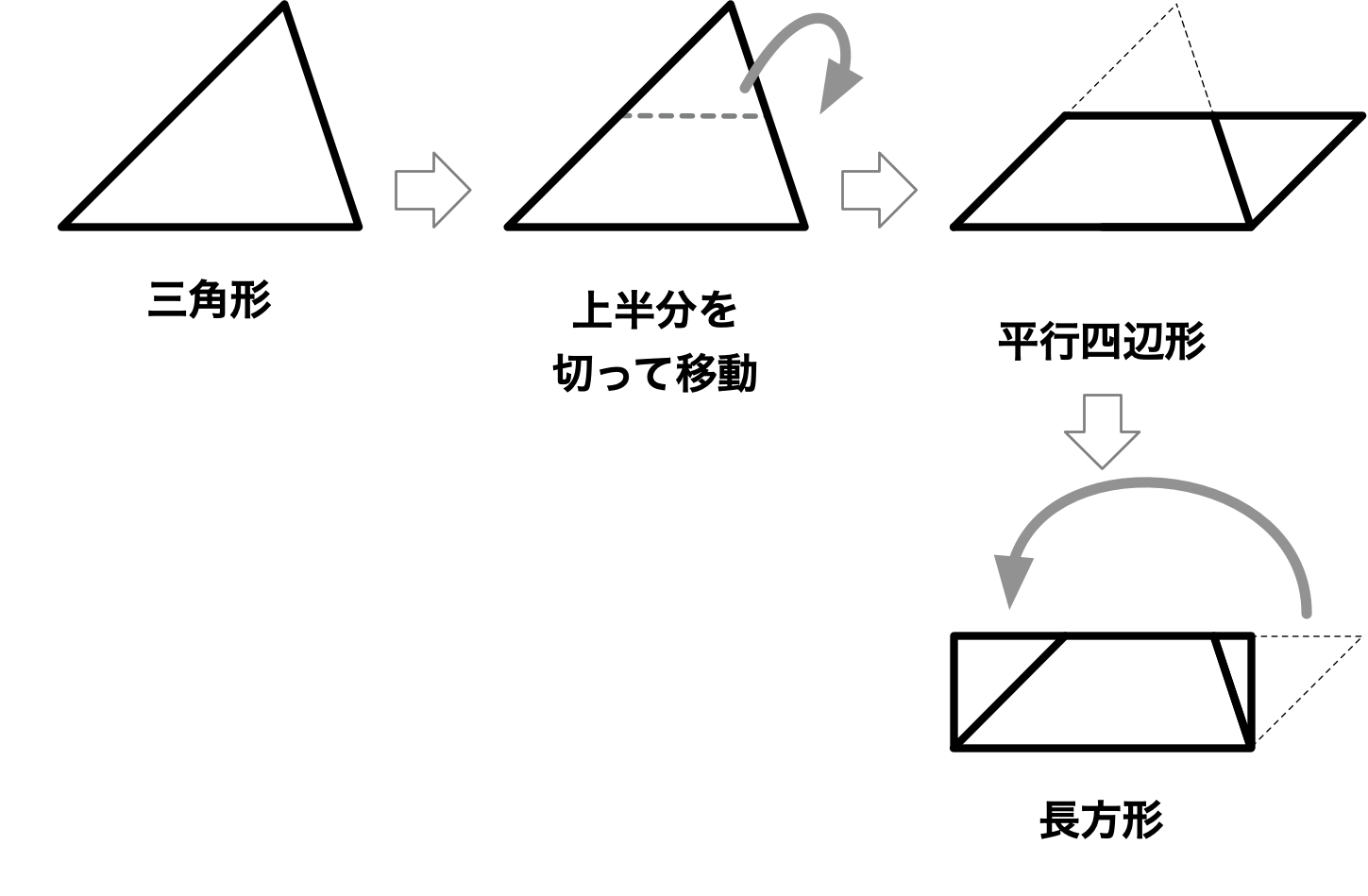
ユーリ「結局は同じじゃん」
僕「ところで、 ユーリの方法は、まず縦に切って二つの直角三角形を作ったけど、 こういう三角形だったらどうする?」
長方形にできる?
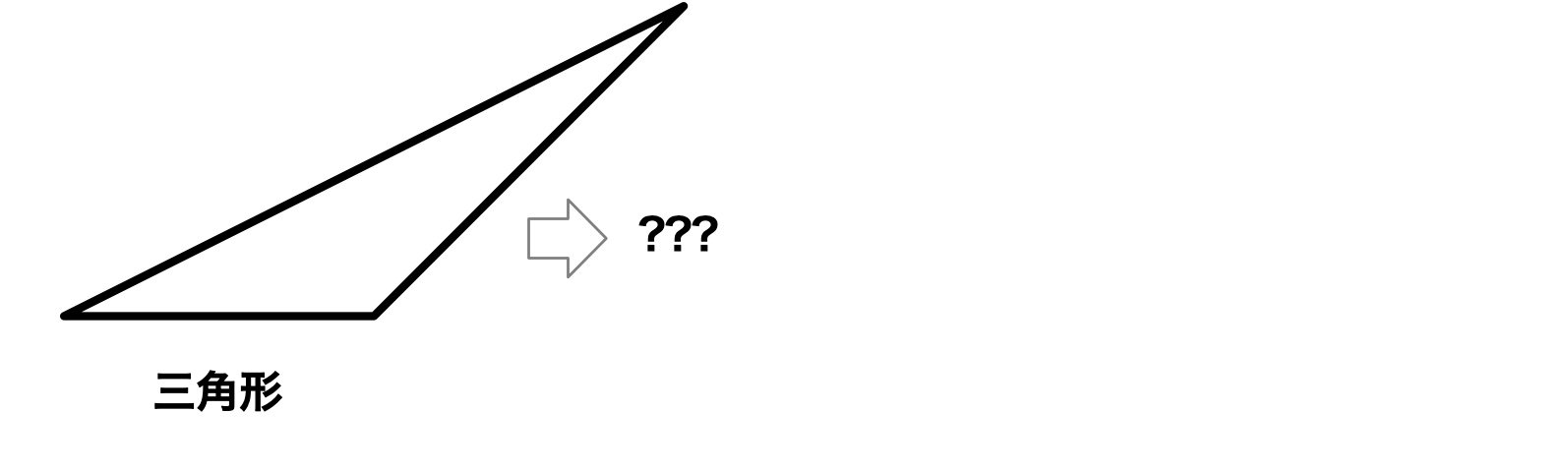
ユーリ「ふっふっふ。ぬかりはありませんぜ、ダンナ」
僕「誰がダンナじゃ」
ユーリ「ちょっと回してやれば同じことでしょ?」
三角形を回してから長方形にする
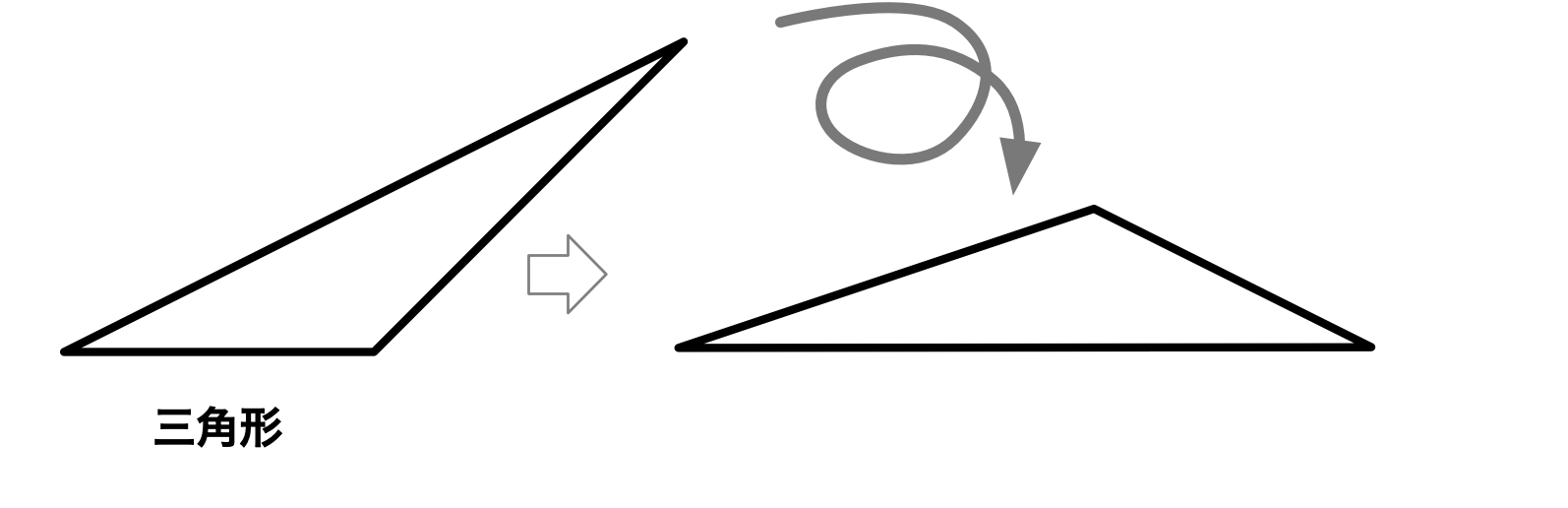
僕「そうだね」
ユーリ「これで、どんな三角形でも長方形にできた!」
僕「これでぜんぶ長方形に帰着できたわけだね」
ユーリ「きちゃく?」
僕「どんな三角形から始めても、ぜんぶ長方形にたどりついたということ。 三角形と同じ面積を持つ長方形を得る方法がわかった」
ユーリ「うん!」
僕「……」
ユーリ「……」
僕「最初にユーリは、直角二等辺三角形を切って移動して正方形を作った。 それから二等辺三角形、直角三角形、一般の三角形を切って移動して長方形を作った。 でも、」
ユーリ「でも、目的は長方形じゃないんだよね?」
僕「そうだね。長方形じゃなくて正方形がほしい」
問題1(再掲)
与えられた三角形に等しい面積を持つ正方形を作図する方法を考えよ。
ユーリ「どんな三角形でも長方形にできるから、 あとは、長方形を正方形に変えることができればいいってことだよね……」
僕「その通り。こんな問題2を解くことになる」
問題2
与えられた長方形に等しい面積を持つ正方形を作図する方法を考えよ。

ユーリ「さっき、かなり考えたんだよ。 でもね、意外と難しーんだよー!!」
僕「どう考えたの?」
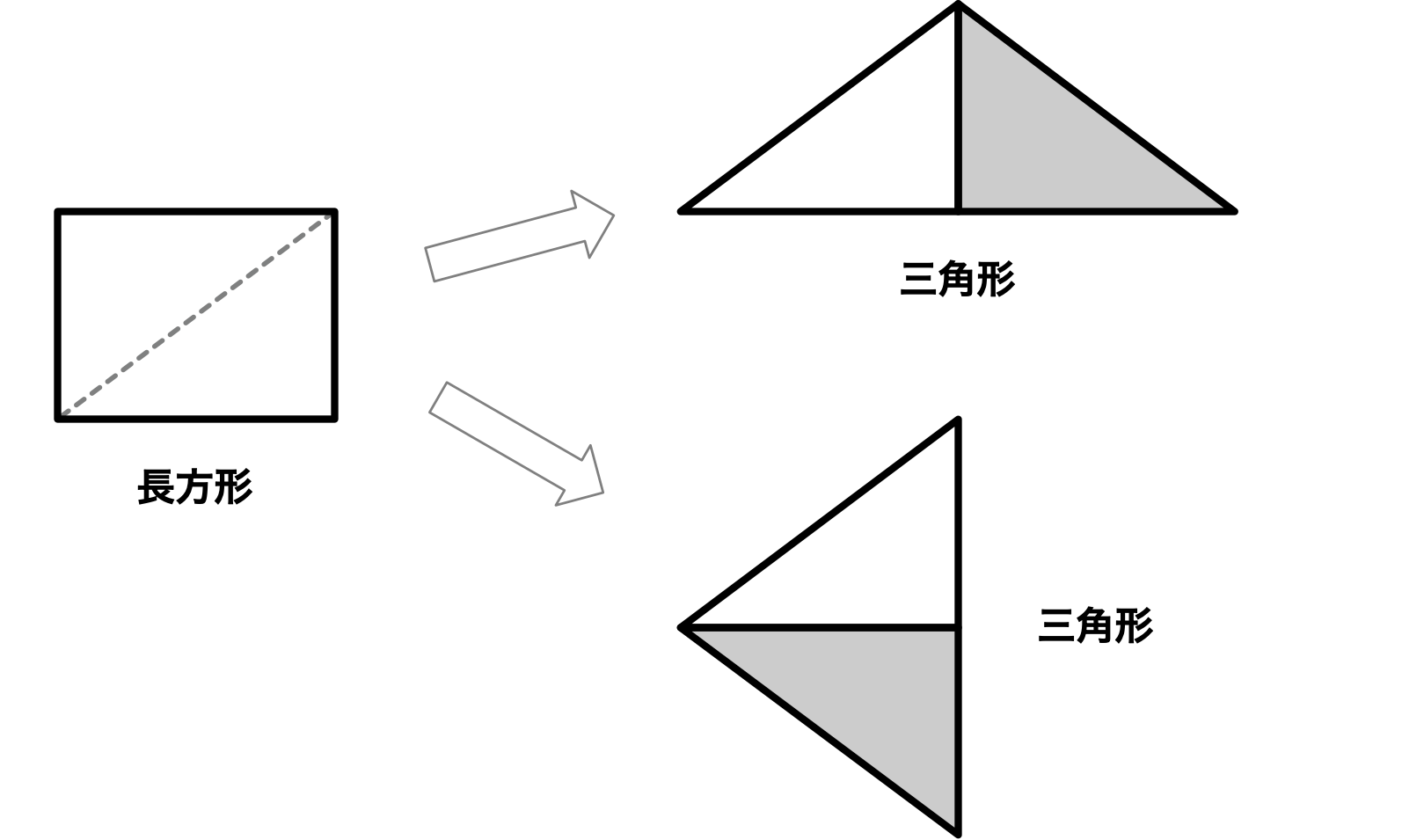
ユーリ「三角形のときは、切って動かせば長方形が作れたよね。 でも、長方形だと、切っても三角形しかできないんだよー」
ユーリの試行錯誤
僕「そうなっちゃうよね。うーん、それじゃあね、たとえば……」
ユーリ「ちょっと待って。お兄ちゃんはこの問題の答え、知ってんでしょ?」
僕「いや、知らないよ」
ユーリ「ウッソ! ……ほんと?」
僕「ほんとほんと。……実は、正直に言うと、ネットでちらっと見かけたことはある。 だから、三角形と同じ面積を持つ正方形の作図ができることは知ってるし、 具体的な作図方法が人類に知られていることもわかっている」
ユーリ「人類」
僕「でも、具体的にどういう手順でやるかは覚えてない。 長方形と等しい面積を持つ正方形を 定規とコンパスだけで作図できることは知ってるけど、 具体的な作図方法までは調べなかったんだ」
ユーリ「んじゃ、ネットで検索する?」
僕「それじゃつまらないよ。もう少し一緒に考えようよ」
ユーリ「うん!……でも、長方形からは三角形しかできないよ」
僕「そんなことないって。それは、対角線で切って移動することしか考えていないからだよね」
ユーリ「むー」
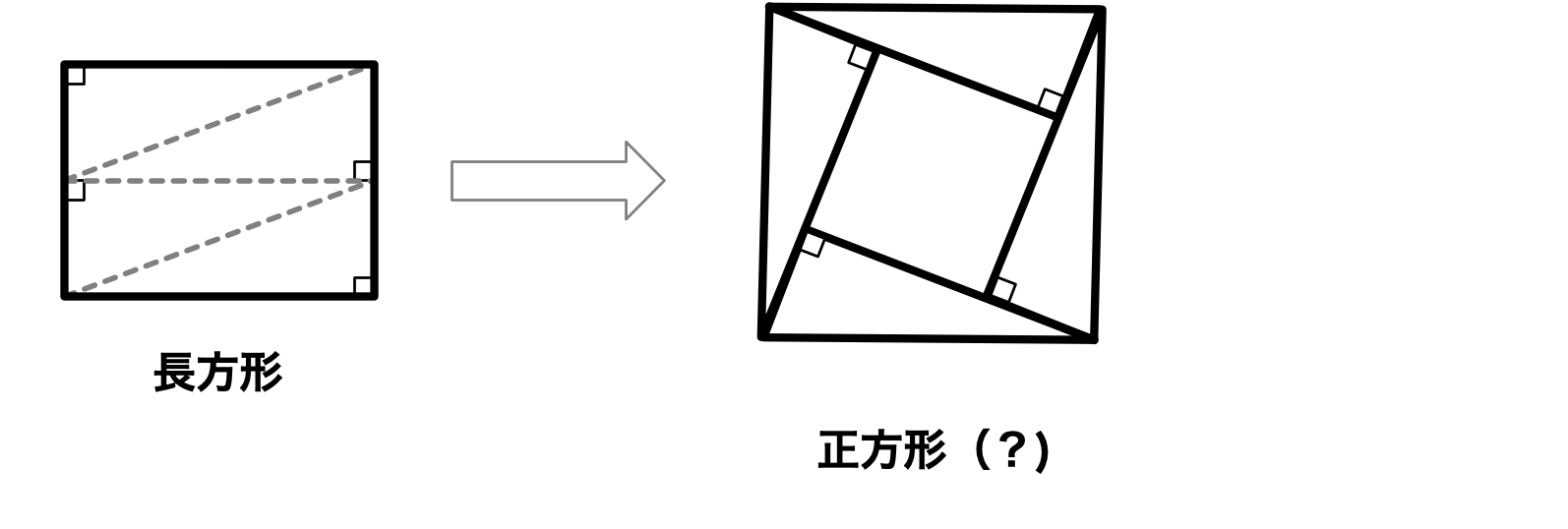
僕「たとえば……うん、こんなふうにすれば正方形ができるよ」
長方形から正方形を作る(?)
ユーリ「いやいやいや、これじゃダメですぜ、センセー」
僕「誰が先生だよ」
ユーリ「これは確かに正方形だけど、面積が大きくなってるよね? 大きすぎる正方形じゃん」
僕「いや、これが大きすぎるのはわかっているよ。 だって中心部に傾いた正方形があるからね。その分だけもとの長方形よりは大きすぎるわけだ。 ただ、正方形を作れば作れるよって……ん?」
そして、今度は僕が深い思考モードに入る。
与えられた長方形の面積と等しい正方形を作図するために。
ユーリ「……で?」
僕「……うん。やっぱり強力な武器を使おう」
ユーリ「『よし、数式を使うぞ! 僕は数式大好きボーイだからな』」
僕「人のセリフを取ると嫌われるぞ。っていうか、そんなセリフは言わないよ」
ユーリ「はいはい……どんな数式を使うの?」
僕「こんな長方形を考えると、長方形の面積は $ab$ になるよね」
長方形の面積
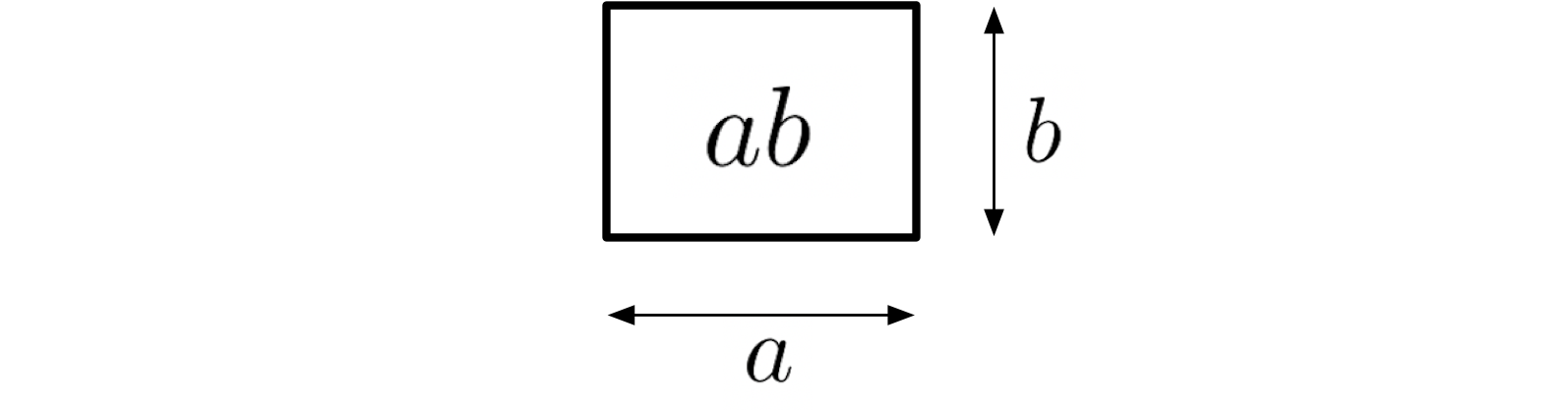
ユーリ「そだね。 $a$ が横の長さで、 $b$ が縦の長さ」
僕「長方形と同じ面積を持つ正方形を作りたいということは、一辺の長さは……」
ユーリ「そかそか、正方形の一辺の長さは $\SQRT{ab}$ になるってことかー」
僕「そういうこと!」
面積 $ab$ の正方形の一辺を求める
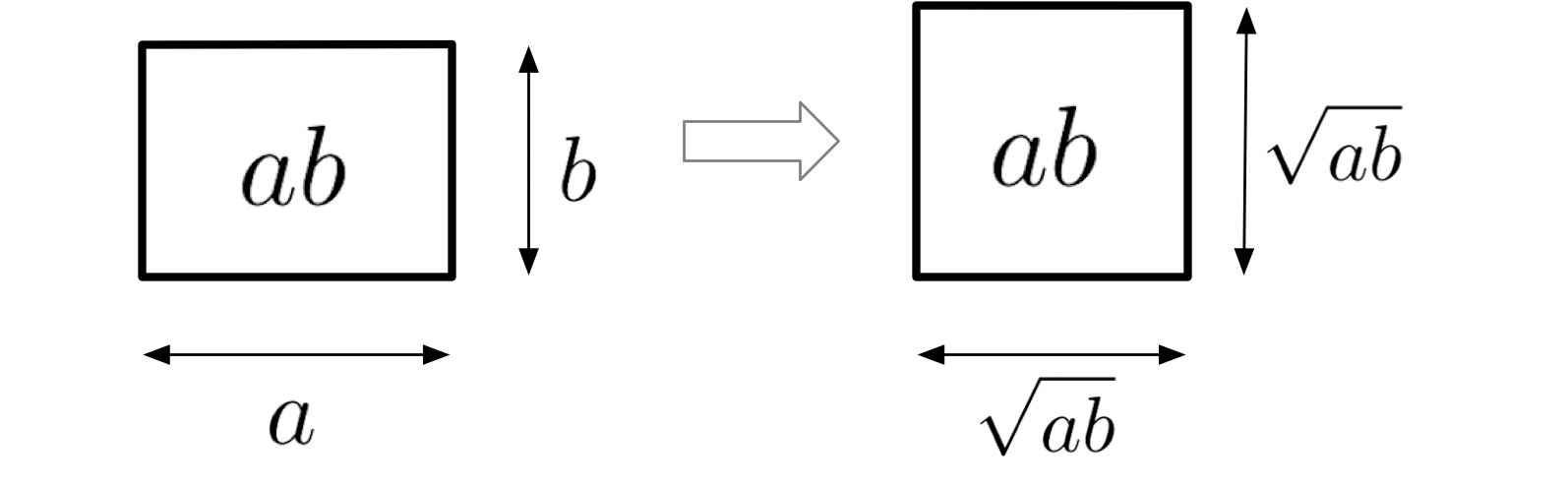
ユーリ「でも、話は簡単になってないよ。ルート?」
僕「うん。僕たちはルートを何とかしたい。そして、何とかできるよ! たとえば、さっき僕が作った《大きすぎる正方形》を思い出す。面積は $ab$ にならないけど、あの《大きすぎる正方形》の一辺の長さは、 $$ \SQRT{a^2 + (\tfrac{b}{2})^2} $$ になるってわかるよね。ほら、ルートが出てくる」
《大きすぎる正方形》の一辺の長さ
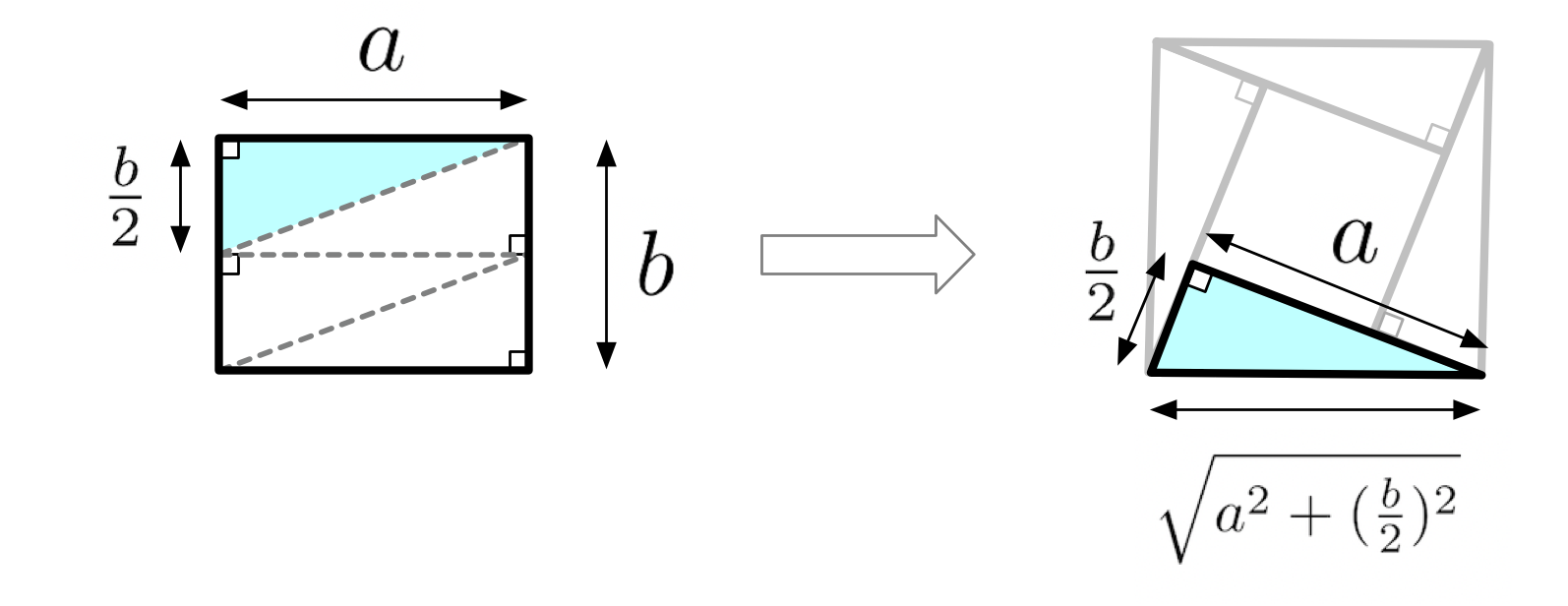
ユーリ「どーしてルートが出てくるかとゆーと……あっ、なんだ、三平方の定理じゃん!」
僕「その通り」
三平方の定理(ピタゴラスの定理)
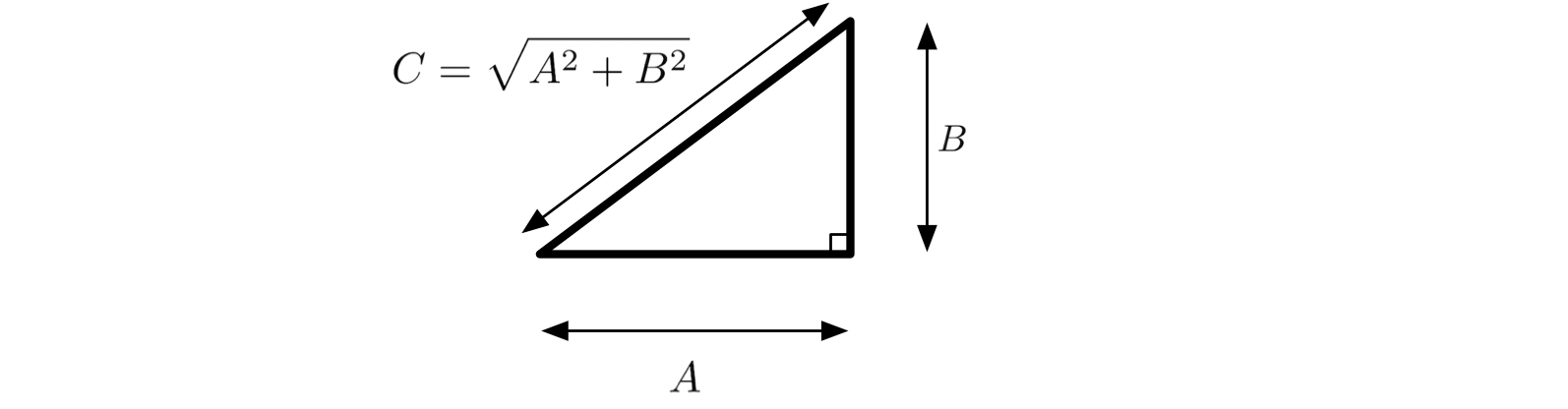
直角三角形の三辺の長さを $A,B,C$ とし、そのうち $C$ が斜辺の長さであるとする。 そのとき、 $$ A^2 + B^2 = C^2 $$ が成り立つ。
$C > 0$ であるから、 $$ C = \SQRT{A^2 + B^2} $$ がいえる。
ユーリ「むむむ……直角三角形を作ればルートが作れる?」
僕「だから、数式の計算をして何とか $\SQRT{ab}$ を作れば、作図の手がかりが得られそうだ」
ユーリ「あっあっ、できそーだよっ!」
ユーリはそう叫んで、再び思考モードならぬ試行モードに入った。
今度は作図じゃなくて、式の変形をしているようだ。
僕も考えよう。

ユーリ「……ダメだあ!」
僕「どうした、ユーリ」
ユーリ「あのね、できそーだと思ったんだけど、ダメだった」
僕「何がどうダメなの?」
ユーリ「わからない……わかりません $\NONA$」
僕「ノナちゃんの真似、やめい」
ユーリ「$\SQRT{ab} = \SQRT{a}\SQRT{b}$ なのはわかるんだけど……」
僕「うん。長方形の辺の長さだから $a > 0, b > 0$ がいえて、 だから $\SQRT{ab} = \SQRT{a}\SQRT{b}$ なのは正しいよ。 ユーリは、まっすぐに $\SQRT{ab}$ を何とかしようと思ったんだね」
ユーリ「お兄ちゃんは違うの? ルートを何とかするって言ったじゃん!」
僕「言ってない言ってない。 ルートはいったん脇に置いておく。 そして、 $ab$ を作ることを考えていた」
ユーリ「へー」
僕「さっきの《大きすぎる正方形》では $a^2 + (\tfrac{b}{2})^2$ が出てきていたから、 二乗の項が出てくる式$$(a + b)^2$$を展開したら、何か出てこないかって試していたんだよ」
$$ \begin{align*} (a + b)^2 &= a^2 + 2ab + b^2 && \REMTEXT{$(a + b)^2$を展開した} \\ (a + b)^2 - a^2 - b^2 &= 2ab && \REMTEXT{$a^2, b^2$を移項してみた} \\ 2ab &= (a + b)^2 - a^2 - b^2 && \REMTEXT{両辺を交換してみた} \\ 2ab &= (a + b)^2 - (a^2 + b^2) && \REMTEXT{カッコでくくってみた($\heartsuit$)} \\ \end{align*} $$ユーリ「$(a + b)^2$ を展開してうにゃうにゃ計算してたってことだよね。何で、そんなことすんの? 意味あんの?」
僕「意味あるかどうかはやってみないとわからないよ。でも $a + b$ は作図できるから、何かが出そうだと思ったんだよ」
ユーリ「うーん……?」
僕「同じように $(a - b)^2$ も計算してみた。それで、できるぞ!ってわかった」
$$ \begin{align*} (a - b)^2 &= a^2 - 2ab + b^2 && \REMTEXT{$(a - b)^2$を展開した} \\ (a - b)^2 - a^2 - b^2 &= -2ab && \REMTEXT{$a^2, b^2$を移項してみた} \\ -2ab &= (a - b)^2 - a^2 - b^2 && \REMTEXT{両辺を交換してみた} \\ -2ab &= (a - b)^2 - (a^2 + b^2) && \REMTEXT{カッコでくくってみた($\clubsuit$)} \\ \end{align*} $$ユーリ「何が? 何ができるの」
僕「$\heartsuit, \clubsuit$ の二つの式を並べて、引き算をする」
$$ \begin{align*} 2ab &= (a + b)^2 - (a^2 + b^2) && \REMTEXT{$\heartsuit$から} \\ -2ab &= (a - b)^2 - (a^2 + b^2) && \REMTEXT{$\clubsuit$から}\\ 4ab &= (a + b)^2 - (a - b)^2 && \REMTEXT{左辺同士、右辺同士を引き算} \end{align*} $$ユーリ「これで、左辺に $4ab$ が来たね……」
$$ 4ab = (a + b)^2 - (a - b)^2 $$僕「うん。 $4 = 2^2$ であることに注意すると、こんなふうに式変形できる」
$$ \begin{align*} 4ab &= (a + b)^2 - (a - b)^2 && \REMTEXT{上の式から} \\ ab &= \frac{(a + b)^2}{4} - \frac{(a - b)^2}{4} && \REMTEXT{両辺を$4$で割った} \\ ab &= \PS{\frac{a + b}{2}}^2 - \PS{\frac{a - b}{2}}^2 && \REMTEXT{$4 = 2^2$だから} \\ \end{align*} $$ユーリ「……左辺に $ab$ が出てきたけど、右辺はごちゃごちゃした式だよ? これを計算するの?」
僕「いや、右辺を計算してしまったら、 $ab$ が出てくるだけだよ。 いま導いたこの式は、どんな $a,b$ についても成り立つ恒等式なんだから」
$$ ab = \PS{\frac{a + b}{2}}^2 - \PS{\frac{a - b}{2}}^2 $$ユーリ「んー……それで、それで? 何だかドキドキしてきたんだけど」
僕「ここで、さっき脇に置いておいたルートを思い出す。 つまり、 $(\SQRT{ab})^2 = ab$ だと考える。すると、こんな式が成り立つことがわかる」
$$ \PS{\SQRT{ab}}^2 = \PS{\frac{a + b}{2}}^2 - \PS{\frac{a - b}{2}}^2 $$ユーリ「んー……あっ!!! これっ、移項したら三平方の定理になるじゃん!!!」
$$ \PS{\SQRT{ab}}^2 + \PS{\frac{a - b}{2}}^2 = \PS{\frac{a + b}{2}}^2 $$僕「そうなんだよ! こんなふうに名前を付けてみると、斜辺が $C$ の直角三角形が現れる」
$$ \begin{array}{ccccc} \PS{\SQRT{ab}}^2 &+& \PS{\frac{a - b}{2}}^2 &=& \PS{\frac{a + b}{2}}^2 \\ \vdots & & \vdots & & \vdots \\ A^2 &+& B^2 &=& C^2 \\ \end{array} $$ユーリ「てことは、 $B,C$ を作ればいい?」
僕「そういうことになるね。 一辺の長さ $B$ が、 $$ B = \frac{a - b}{2} $$ となって、斜辺の長さ $C$ が、 $$ C = \frac{a + b}{2} $$ となるような直角三角形を作図できれば、 もう一辺の長さ $A$ が求める長さ、つまり、 $$ A = \SQRT{ab} $$ になる」
ユーリ「数式、すっごーい! $a,b$ から $B,C$ は……作れそう!」
僕「うん、作れる。コンパスと定規で作れるよ。作ってみよう!」
ユーリ「おー!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第351回終わり)
(2022年4月1日)